蒙特卡罗方法的原理及在数值计算方面的应用——以定积分为例

李 姣 娜

(重庆电子工程职业学院,重庆 401331)

对于求解积分、代数方程，线性方程组、中心极限定理等问题，常规的数学解法一般可以很好地帮助我们解决，但有些公式的计算数据较为庞大或复杂难解，这就为处理问题带来困扰。而研究客观现象或分析一个系统时，可以先构造一个与该现象或系统相似的模型，通过在模型上进行实验来研究原模型，这就是模拟。随机系统可以用概率模型来描述并进行实验，这就是随机模拟方法。我们常见的道路交叉口的红路灯的交替时间就是随机模拟的结果。

1 蒙特卡罗方法的起源

2 蒙特卡罗方法的基本特征

2.1 蒙特卡罗方法的思想

用蒙特卡罗方法解决问题的基本思想是：

1)根据提出的问题，构造或描述一个相关的概率模型或随机过程，使问题所需求的解与构建的模型中的一些统计值(如概率、均值或方差等)保持一致，所构造的模型在主要特称参量方面也要与所求问题相一致；

2)根据模型中各个随机变量的分布，适当地从已知分布的母体中抽样，在计算机模拟中生成随机数；

3)建立估计量，获取结果，即根据随机过程建立某些估计值，大量重复试验，对其比较分析，最终给出问题的最优概率解，从而得到问题的近似值。

不难看出，与传统的数学统计方法相比较，蒙特卡罗方法借助计算机减缓了实现的困难，且可操作性强、直观易懂。而其他数学方法较难处理甚至不能处理的复杂问题，它都可以找到恰当的方式来处理。

2.2 蒙特卡罗方法的原理

蒙特卡罗方法的基本过程就是通过随机数的抽样值xi(i=1,2,…，N)，构造未知待求量的估计值。其中最主要的理论依据为中心极限定理[3]。

随机变量xi(i=1,2,…，N)彼此独立同分布，并且均值为E(xi)=μ，方差为D(xi)=σ2，当N充分大时(N→∞) ，有

即当N充分大时，对于给定概率1-α(α为给定显著水平)，有

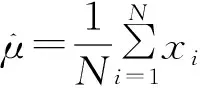
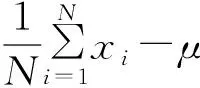
3 蒙特卡罗方法在数值计算方面的应用

3.1 理论基础

随着计算机的日益普及和信息技术的突飞猛进，蒙特卡罗方法在数学、机械、金融、医学等领域的应用越来越广泛，它已经成功解决了许多经典的数学和物理问题，尤其在物理过程、原子能技术、武器装备论证[4]等问题和相关领域的科学研究中发挥了极其重要的作用，体现了很高的应用价值。

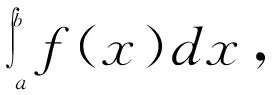
(1)

从式(1)中可以看出，蒙特卡罗方法需要进行大量的随机模拟，其精度与样本容量N有直接关系。随着计算机技术的快速发展，该方法的计算成本劣势已逐渐淡化。

3.2 应用举例

3.2.1 随机投点方法

对(0,1)区间均匀分布随机数抽样(如图1)，抽样值为ξi，对(0,M)区间均匀分布随机数抽样(任取常数M≥f(x))，抽样值为ηi，且当ηi≤f(ξi)时，点(ξi，ηi)落入曲线y=f(x)下方，其中i=1,2,……，N。

3.2.2 重要度抽样方法

在重选样中我们选择重砂1、重砂3、重砂5及重选尾矿进行了全方位考察。铌钽矿物、黄铁矿等金属硫化物及其他比重较大的矿物主要富集于重砂1中，为此又对重砂1进行了浮选分离(表6)，分离出以硫化物为主的硫精矿(浮硫精)和以氧化物为主的硫尾矿(浮硫尾)。重砂5中除石英外，云母含量亦较高，云母为铷的重要载体矿物，故我们对重砂5中云母进行了浮选富集。重选尾矿样经X衍射分析结果表明，成分主要为云母、石英和长石类矿物。

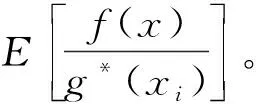
3.2.3 平均值方法

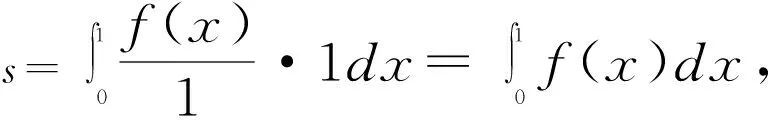
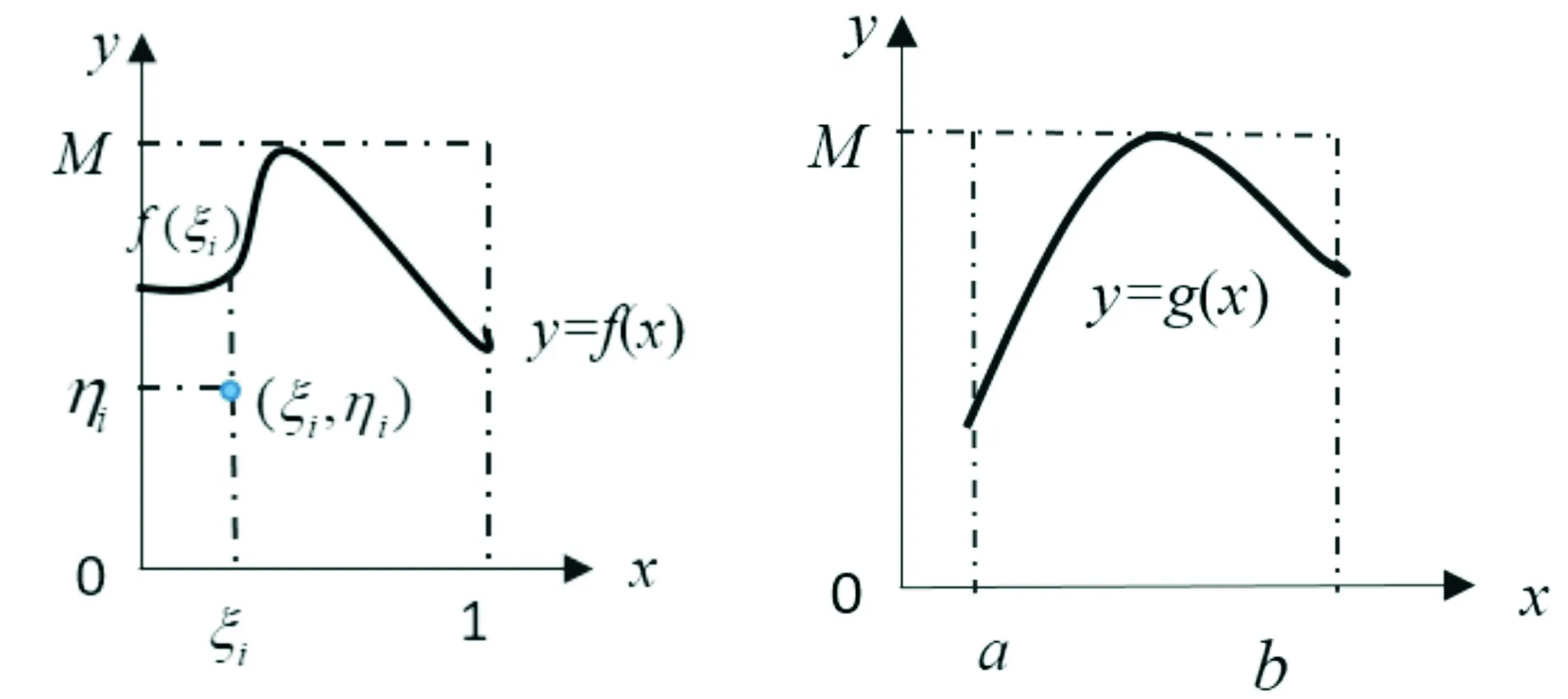
图1 随机投点方法示意图 图2 (a,b)上定积分的示意图

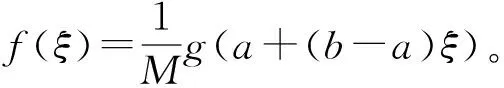
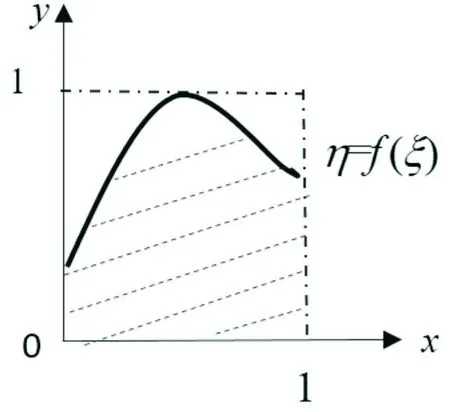
图3 (0，1)上的定积分示意图

3.3 随机模拟

function jifen=jifen(N)

n=0;

for i=1:N

x=rand;

y=rand;

if y

n=n+1;%累加小球落入阴影部分次数

else

n=n;

end

end

n

p=n/N

图4 程序编写示意图

表1 程序运行结果

可见，当模拟的试验次数较少时，其结果与真实值有一定误差，而试验当超过 次，其模拟的结果和真实值1/3很近似。

结论

可以看出，利用蒙特卡罗方法求解本来不具随机性质的确定性的实际问题，例如计算定积分，解线性方程组等问题，主要是人为构造一个随机过程，建立估计量，使其期望值正好是所求问题的解，最后根据所构造的概率模型编程计算，获得结果。该方法在概率研究和计算机运用方面有值得借鉴的意义。