滚子分布方式对球面滚子轴承服役性能的影响
刘学婧,刘磊,2,徐华,张胜伦,邢宇
(1.西安交通大学机械工程学院,710049,西安;2.浙江大学流体动力与机电系统国家重点实验室,310027,杭州;3.西安工程大学机电工程学院,710048,西安)
由于风力发电设备承受的载荷较大,且受到实时风力、风速和风向变化的影响,会使得用于支撑以及传动用的转子系统出现挠曲现象。转子挠曲会直接导致支撑轴承承受附加弯矩,进而降低轴承使用寿命,而运动副一旦损坏,轻则会引起机构振动加剧,重则直接造成机构损坏,而具有调心功能的轴承则能很好解决上述问题。
如图1所示,双列外球面滚子轴承(以下简称球面滚子轴承)主要由内圈、外圈、滚动体、保持架等几部分组成。与其他类型滚动轴承最大的不同在于,凭借外圈内壁的球形结构以及椭球形的滚子,球面滚子轴承可以实现内圈相对于外圈在三维空间内自由旋转,从而自动抵消由于转子挠曲或轴承内外圈角度不对中所引起的附加弯矩,即自调心功能。由于内外圈之间没有约束关系,所以球面滚子轴承不能承受弯矩。另外,球面滚子轴承的滚动体为滚子,且双列布置,因而径向承载能力极强;但轴向承载能力偏弱,仅用于承担预紧力或是偶然的、小幅值的随机载荷。球面滚子轴承一般体积、质量偏大,不易安装和搬运,工作转速较其他类型滚子轴承偏低。
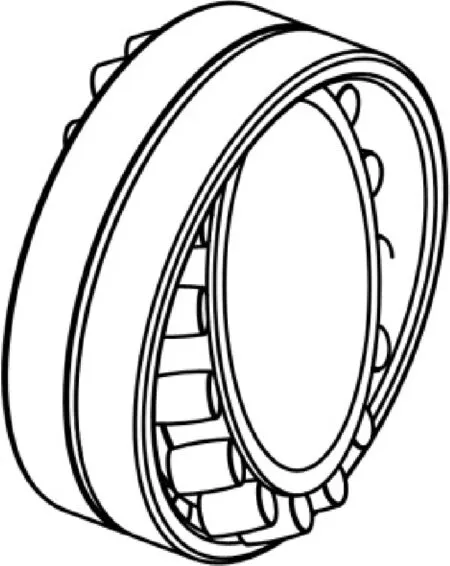
图1 球面滚子轴承
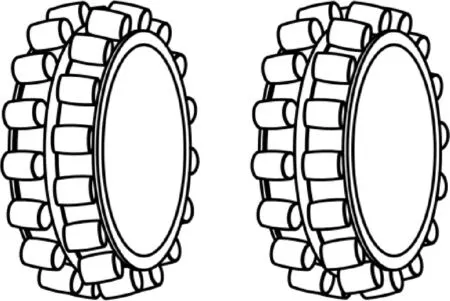
(a)交错式 (b)平行式
对于球面滚子轴承而言,滚子分布方式有交错分布和平行分布两种,如图2所示。现阶段对于球面滚子轴承滚子分布方式的研究已经有了初步的进展。Bercea等建立了统一的双列滚子轴承静力学模型[1],不仅表征了不同类型的滚子分布方式,建模方法也适用于分析球面滚子轴承。在此基础上,Sakaguchi等加入了离心力和陀螺力矩等因素,构成了典型的拟静力学分析模型[2-3]。Yang和Ghalamchi等考虑了质量项和阻尼项,提出了基本的动力学方程[4-5],以此模拟不同滚子分布方式下的球面滚子轴承内圈动态特性。Ghalamchi等特别指出,对于径向载荷而言,交错分布的滚子更易降低内圈振动幅值。Cao等人建立的动力学模型[6-7],不但考虑了内圈的运动状态(假设外圈固定),还考虑了滚子在法向上的振动,方程数从基本的3自由度扩展到3+N自由度,其中N代表每个滚子的法向移动自由度。Cao的模型仅考虑了交错式滚子分布方式,因而得到的结论并不适用于两列滚子相对独立公转的情况。An等在传统的力学建模方法外,提出了一种故障诊断方法检测球面滚子轴承的振动特性,并以此构建数学模型[8-9]。Xian对测出的振动信号分类,并进行回归分析,拟合成球面滚子轴承的振动模型[10]。An和Xian是以特征信号来建模,导致模型并没有重点关注轴承的几何形状,因此并未着重分析滚子分布方式对特征信号带来的影响。
另有一些学者采用已经成熟的商业软件进行球面滚子轴承的建模。文献[11-13]分别利用Workbench建立了球面滚子轴承的模型,并完成了疲劳寿命、接触应力及优化设计等方面的分析,认为交错分布和平行分布在静力学分析结果上并无本质区别,只是在受力位置和幅值上略有不同,这是由于滚子的位置角不同而造成的。马方波等建立了能够表征球面滚子轴承滚子分布方式的静力学模型[14-15],也得出了类似的结论,交错分布下单个滚子所受的最大载荷略小于平行分布下单个滚子所受最大载荷。张娄红等对经典赫兹线接触和Workbench的计算结果进行了对比,发现两者的计算误差较小[16],为球面滚子轴承的几何结构设计、优化滚子分布方式等工作提供了理论支持。Fiedler等使用ADAMS建立球面滚子轴承的多体动力学模型[17],并研究了交错分布式的滚子与滚道之间的接触状态与摩擦功耗。Houpert重点考虑了单个滚子与滚道的接触状态[18],并未指出滚道与多个滚子的联合作用规律。
在实验方面,Goodelle等观测了滚子与滚道的接触状态与接触区形貌[19],但静态实验结果难以获得轴承的振动特性,也就无法获得滚子分布方式对轴承实际服役性能的影响。Royston等测试出了球面滚子轴承径向和轴向刚度及两向的交叉刚度,重点介绍的是其提出的测试刚度阻尼的实验方法[20]。赵景周通过对径向游隙的测量,可以清楚地了解到不同形式分布的滚子在通过承载区时的跳动状态具有明显差异[21]。Desavale等仅测试了平行分布式球面滚子轴承的动态数据[22],因此无法获知交错式滚子分布对于轴承服役性能的影响规律。考虑到交错式和平行式滚子分布方式会显著影响轴承的服役性能,因此Houpert所获得的经验公式[23]对于平行式滚子分布的轴承来说并不适用。Maruschak等重点关注的是疲劳破坏的演化规律[24],而局部疲劳破坏与滚子分布方式并无直接关联。
综上所述,文献大都认为两列滚子交错分布可以在通过承载区时滚子交替承担外部载荷,因而服役平稳。平行式滚子方式因为相邻滚子间的跨距略大,导致滚子以一个跨越的方式通过承载区,因而会出现较大的振动。但是,上述结论的前提是球面滚子轴承仅承受径向载荷,而实际工况下,轴承往往会承受一定的轴向力,因此上述结论并不充分。此外,现有文献大多忽略了调心工况这一特征,认为调心工况属于故障工况,因此在模型中并未考虑调心作用的影响。再者转子挠曲是由于外载荷过大而造成的,在实验室的单一环境中难以提供足够大的外载荷,因此如何设计具有自调心功能的实验台是需要研究的问题。
本文以适用于调心工况下的球面滚子轴承为研究对象,首先建立动力学模型,在考虑轴向外载荷、自调心功能的前提下,研究球面滚子轴承滚子分布方式对服役性能的影响,并设计具有自调心功能的实验装置验证理论结果的正确性。
1 数学模型
1.1 单个滚子的受力分析
轴承的主要受力位置为滚子与内圈、外圈滚道之间的接触区。假设接触体在应力的作用下呈现小变形状态,则该接触区可视为是一个平面。为了便于计算,用矩形单元对该接触区进行网格划分。同时每个接触区都有自身的局部坐标系,且各局部坐标系之间相互独立:对于第i个滚子来说,接触区内的xi和yi方向分别定义为平行和垂直滚子的滚动方向;而zi方向则垂直于xioiyi平面。根据赫兹接触理论,在接触区内任意单元的弹性变形等于柔度系数乘以力,而这个力是接触区内对应单元应力的积分,变形表达式如下
(1)
式中:ω是某一单元的弹性变形;(x,y)、(x′,y′)表示该单元的坐标;ν为泊松比;E为弹性模量;S为接触区的面积;p为某一单元的应力。
假设划分的网格足够细,那么每个网格的应力可视为恒定,此时式(1)可改写为
(2)
式中:Fk为柔度系数,可表示为
(3)
其中,角标j、k代表接触区中任意两个单元,那么j单元的变形引起k单元产生的应力为
(4)
压力等于网格面积乘以应力
Qk=4abpk
(5)
式中:a、b分别为矩形单元的长和宽。
弹性变形ωj亦可表示滚子与内圈、外圈滚道之间的弹性变形与两者初始距离之间的差值
ωj=δi-κj
(6)
滚子与滚道之间的弹性变形δi可表示为
δi=D-D0
(7)
式中:D与D0分别表示受载前后滚子与滚道之间的距离
D0=Rw-Ri
(8)
其中Rw是滚道半径,Ri表示第i个滚子的半径。
Dx=D0cos(α0+αS)sinφi+δXsinφi
(9)
Dy=D0cos(α0+αS)cosφi+δycosφi
(10)
Dz=D0sin(α0+αS)+δz
(11)
式中:α0为初始接触角;αS为自调心接触角。考虑到每个滚子的位置不同,自调心接触角可表示为
αi=αS(1-φi/90)
(12)
由于两列滚子的分布方式不同,因此不同列滚子的位置角φi也不同,表达式如下
(13)
(14)
式中:φ0表示两列滚子分布差异,当两列滚子平行分布时,φ0=0,反之交错分布时,φ0=π/Z;Z为单列滚子个数。
滚子与滚道间可看作两个弹性体V1、V2相接触,如图3所示。两者之间的初始距离可表示为
(15)
至此已经算出接触区内任意单元所受的载荷,滚子与滚道之间的作用力即为同一接触区内所有单元作用力之和
2009年入秋以来,我国云南、贵州、四川等西南地区发生了百年一遇的严重干旱,旱情持续时间之长、受灾面积之大、影响范围之广引起了党中央、国务院的高度重视。胡锦涛总书记对抗旱救灾工作作出重要指示,温家宝总理深入旱灾最严重的地区指导抗旱救灾工作,回良玉副总理等中央领导也多次作出重要指示,水利部部长陈雷强调要认真贯彻落实中央领导重要指示精神,把抗旱工作作为当前水利工作的重中之重,举全部之力、全行业之力,全力以赴做好抗旱减灾各项工作。
Qi=∑Qk
(16)
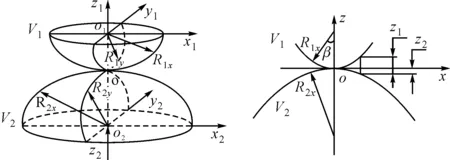
(a)赫兹接触模型 (b)接触区形貌
1.2 构建动力学方程
根据上述分析建立振动方程如下
(17)
式中:M为轴承质量;C为轴承阻尼系数;w为轴承列数;Z为单列滚子个数。
式(17)的第3项是用所有滚子的受力之和代替了位移与刚度的乘积。考虑到球面滚子轴承在服役时会受到x、y、z3个方向的外载荷,但不承受弯矩,因此将式(17)扩展如下
(18)
(19)
(20)
式(18)~(20)可用龙格库塔法进行求解。
1.3 机构挠曲程度和自调心接触角的估算
球面滚子轴承主要优势在于能够自动抵消由于转子挠曲所带来的附加弯矩,因此转子的挠曲情况直接决定了球面滚子轴承自调心接触角的方向和幅值。相比于其他文献,本文根据已知工况条件对转子的挠曲程度和球面滚子轴承自调心接触角进行估算,而不是任意取值,可获得更为准确的仿真结果。
对于单一变量的轴承刚度及多变量下的轴承刚度,如3自由度,可分别表示如下
(21)
(22)

图4 转子任意一个单元的位移及角位移自由度情况
转子的刚度采用有限元法来获得。将转子分为若干个单元,假设每个单元有两个节点,每个节点有两个自由度,分别是径向线位移自由度和角位移自由度,如图4所示。根据有限元理论,获得梁单元的刚度矩阵为
(23)
式中:Kr是转子第i个单元的刚度矩阵;E是转子的弹性模量;l是转子第i个单元的长度;Ir表示转子第i个单元的惯性矩,值为
(24)
式中:Dr为转子截面的直径。
在轴系中,轴承与转子属于并联关系,共同支撑了外载荷。那么轴承-转子系统的总刚度等于对应位置节点上轴承刚度与转子刚度的线性叠加,即
(25)
式中:K为轴承-转子系统总刚度矩阵;Kb为支撑轴承的刚度矩阵。
当获得系统总刚度与外载荷后,即可获得各节点位移,并可计算轴承及转子所受的载荷,若满足判定条件则计算结束。判定条件分为两部分:一部分是每个轴承所受的载荷要等于转子对应位置节点上的载荷;另一部分是以上两部分的合力要与外载荷相等
(26)
若不满足条件,则对轴承刚度进行修正。然后利用本次计算获得的节点位移求出新一轮的轴承刚度,并与上一次的轴承计算刚度加权平均,得出新一轮计算所需的轴承刚度分量
kt+1=kt-1(1-λ)+kt
(27)
2 结果与讨论
2.1 滚子分布方式对轴承振动的影响
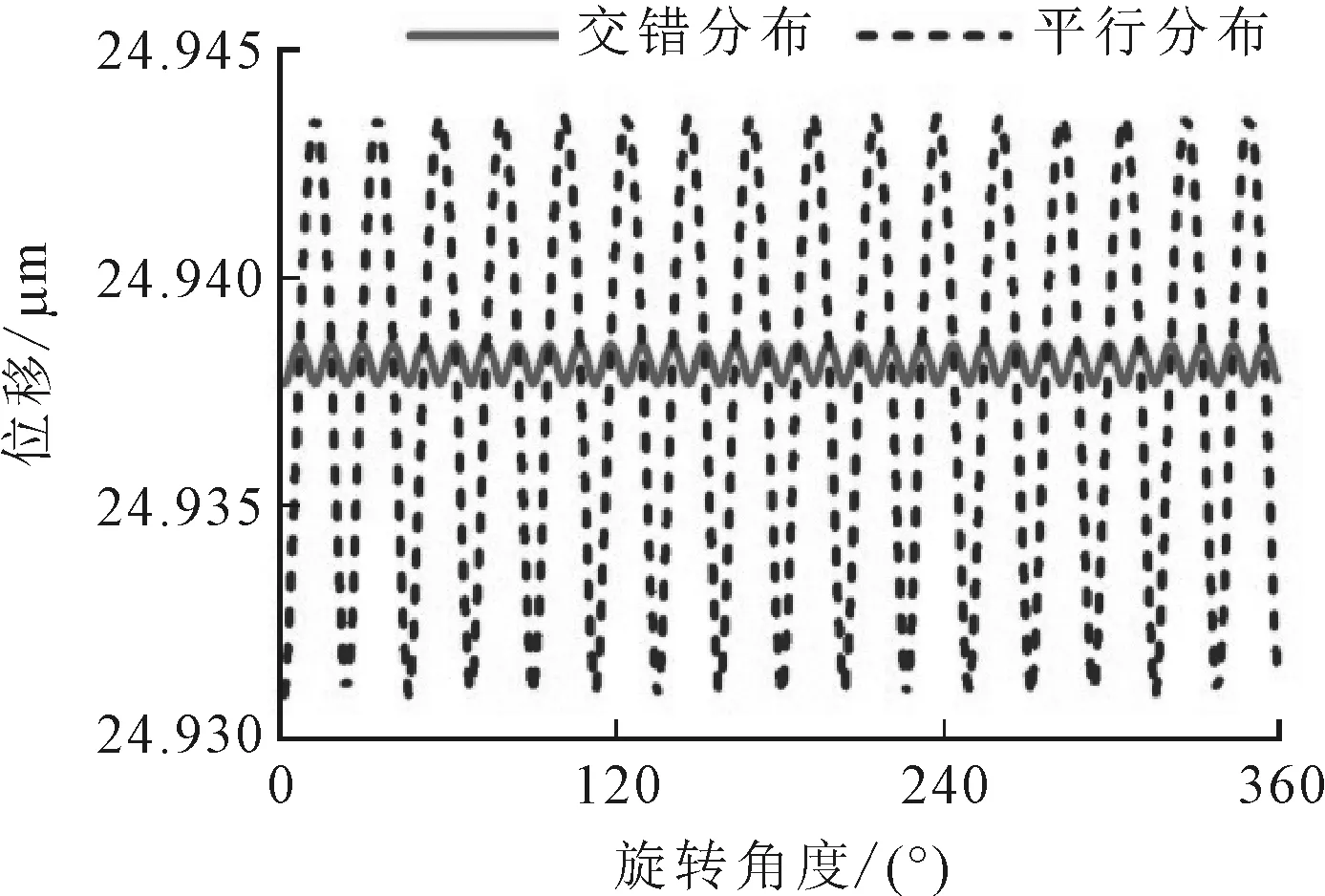
(a)无轴向载荷且初始接触角为7.92°

(b)轴向载荷为500 N且初始接触角为7.92°

(c)轴向载荷为1 kN且初始接触角为7.92°

(d)轴向载荷为1 kN且初始接触角为12.92°
球面滚子轴承一般有平行分布和交错分布两种方式,现有文献大多认为,交错式分布的滚子将更利于球面滚子轴承服役稳定性[5],如图5a所示(仿真过程中径向载荷设定为50 kN),但这一结论的前提是球面滚子轴承只承受径向载荷。实际工况下,球面滚子轴承不可避免地会受到轴向载荷的冲击。如图5b所示,当径向载荷幅值不变、轴向载荷为500 N时,交错分布滚子所对应的轴承位移振荡范围明显增大,而平行分布滚子所对应的轴承位移振荡范围没有明显的变化。当轴向载荷继续增大至1 kN时,见图5c,平行分布滚子的振荡范围要明显小于交错分布滚子的振荡范围。
平行分布的滚子在轴向上的刚度更大,因而可以更好地抵抗一定范围内的轴向载荷冲击。所以,对于以外部径向载荷为主的工况,建议球面滚子轴承采用交错式滚子分布方式;而对于有频繁轴向冲击的工况,建议轴承采用平行式滚子分布方式。另外,考虑到滚动轴承的轴向承载能力与初始接触角成正比,所以适当增大初始接触角,也可以在一定程度上降低交错分布滚子的位移振荡范围,如图5d所示。
为了突出调心作用对特征频率的影响,避免外部载荷对特征频率幅值的干扰,将图6仿真中载荷初始值设定为径向载荷为20 kN,轴向载荷为200 N。

表1 轴承几何参数与材料参数

(a)交错分布且自调心角为-2°

(b)平行分布且自调心角为-2°

(c)交错分布且自调心角为3°

(d)平行分布且自调心角为3°
由图6轴承振动的频域特征对比可以看出,不论滚子是交错分布还是平行分布,特征频率(主频)都约等于单列某一滚子通过外圈某一点的频率,即约等于单列滚子数与滚子公转频率的乘积。从主频的幅值上看,当轴承处于调心工况时,交错分布的滚子更利于轴承服役的稳定性。不论是交错分布还是平行分布,在调心作用明显的情况下,都会激发出附加频率,频率值约为主频加、减滚子公转频率的整数倍。总结上述规律可得附加频率的频率值表达式如下
fa≈fr±qfc
(28)
式中:fa为附加频率的频率值;fr为转子的频率值,即主频;q为一个正整数;fc为滚子公转频率。通过对附加频率的判别,可以确定球面滚子轴承是否处于调心工况。
2.2 滚子载荷分布
假设轴承在某一时刻受到50 kN的径向载荷,以及200 N的轴向冲击载荷。鉴于轴向载荷对球面滚子轴承的服役特性影响较大,图7列举了此种工况下轴承滚子的轴向载荷分布,可以看出,两种滚子分布形式下的轴向载荷分布情况大致相同。说明由于滚子分布方式不同所造成的轴承振动差异并不是因为滚子受力不同,而是不同滚子分布形式下,滚子通过承载区的状态不同所造成的,即一种是交替通过,另一种是并排跨越通过。
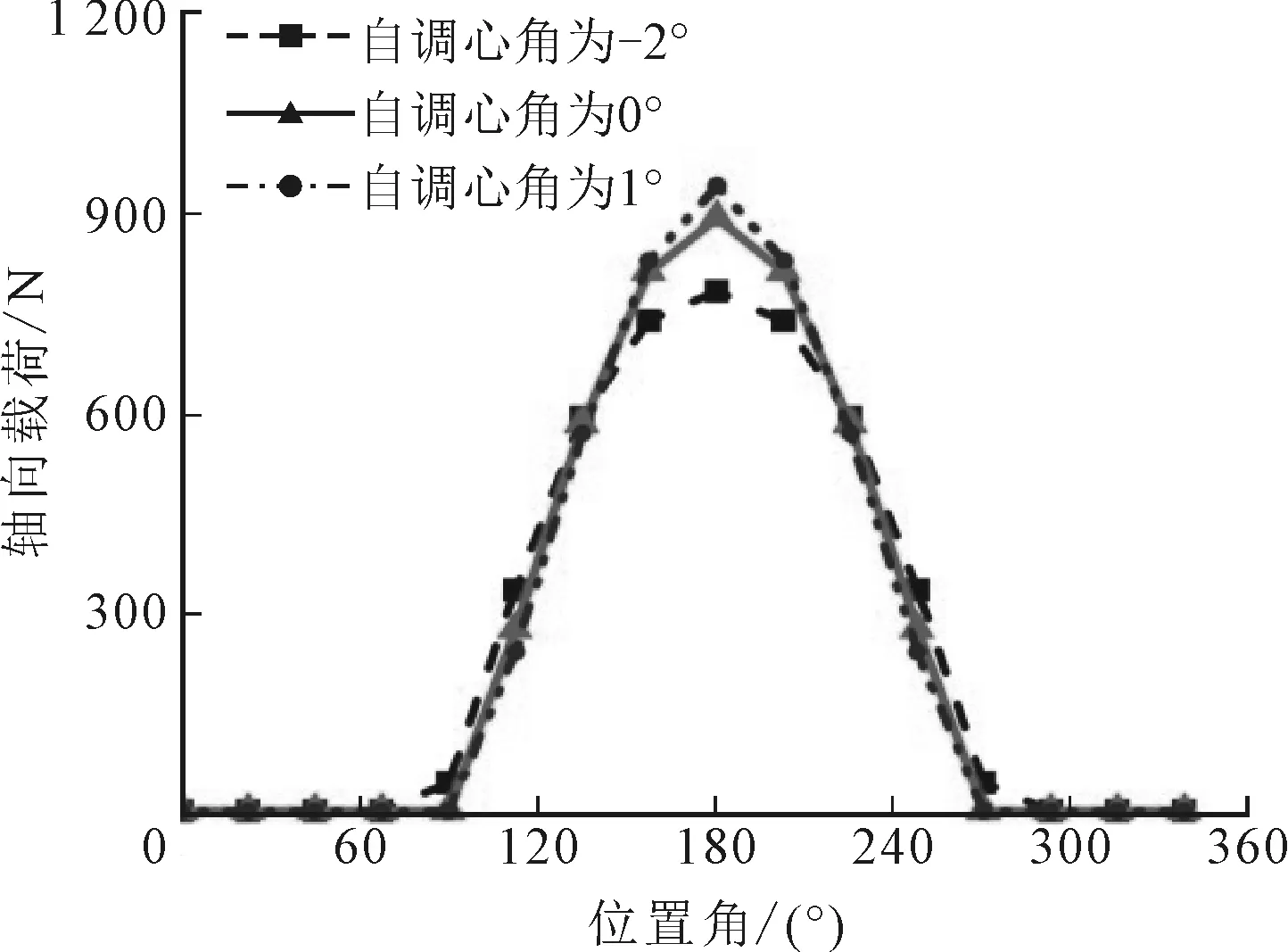
(a)交错分布方式下左侧列载荷分布

(b)交错分布方式下右侧列载荷分布

(c)平行分布方式下左侧列载荷分布

(d)平行分布方式下右侧列载荷分布
由图7还可以看出,自调心作用会导致两列滚子受力不均,即出现偏载情况,偏载的方向会因调心角度的不同而不同。轴向力本身也会使轴承出现偏载情况,因此当以上两种因素叠加时,会出现偏载加剧或抵消两种结果。
考虑到球面滚子轴承存在一定的初始接触角,部分径向载荷会因为接触角而转化为轴向力,因此单个滚子所受的轴向力有大于外部轴向冲击载荷的可能。
3 实验验证
待测试轴承为22215型斯凯孚(SKF)轴承和瓦轴(ZWZ)轴承,见图8。ZWZ轴承属于滚子交错分布的形式;SKF轴承两列滚子之间没有约束关系,因此并不完全属于滚子平行分布,但在安装过程中,尽量使对应滚子保持平行状态。

图8 待测试轴承
实验台的总体布局如图9所示。转子由两个参数相同的滑动轴承所支撑,转子后端由电机带动旋转,前端预留位置布置待测轴承。实验设计原理如下,将轴承座的内圈卡具固定在转子上,并依次在内圈卡具上安装待测试轴承和外圈卡具,外圈卡具不加任何约束,仅通过球面滚子轴承内外圈之间的几何结构进行调心。这样设计的好处在于即使在实验室条件有限的情况下(施加的外载荷有限),也能实现调心工况。缺点在于,由于轴承座的内圈卡具并非完全约束,会随着转子进行小幅振动,而外圈卡具为了实现调心工况,没有施加任何约束,属于浮动状态,因此得到的测试结果偏大。在自调心轴承座的外圈卡具上设有吊环,通过吊环连接加载装置,包括拉力传感器、加载支架以及质量块等等,以加载装置8沿径向垂直方向(纵向)提供外部径向载荷。位移传感器分别从径向水平(横向)和径向垂直(纵向)两个方向对轴承振动信号进行采集,并将采集到的数据实时传输到电脑中进行处理并保存。
实验工况如下,待测试轴承为22215型球面滚子轴承,实验过程中,轴承受到径向载荷约为430 N,转子转速约为320 r/min,测试结果如图10所示。从图可以看出,两种轴承的主频都约等于单列某一滚子通过外圈滚道的频率,且交错分布滚子所对应的主频幅值较低。另外,在轴承服役过程中,由于调心作用所引起的附加频率也较为明显,附加频率约等于主频加、减滚子公转频率的整数倍。该结论与图6和式(28)所得出的规律相符,从而证明了本文理论计算结果的合理性。

(a)滚子交错分布的ZWZ轴承
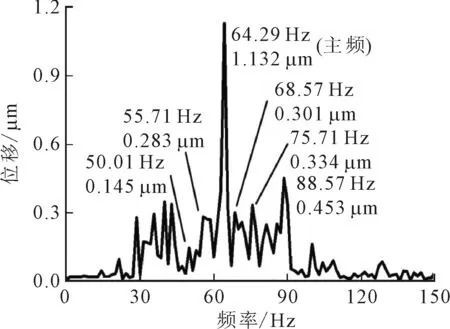
(b)滚子平行分布的SKF轴承
需要说明的是,轴承在实际工况下的服役性能会受到多种因素的影响,比如除了滚子的分布方式外,还会受到微尺度设计参数、轴承加工工艺参数、外部工况载荷的大小和方向等因素的影响。本实验所关注的仅仅是球面滚子轴承滚子分布方式,特别是在调心工况下对轴承服役性能的影响,因此本文的结论都是以此为前提所获得的。
4 结 论
本文以双列外球面滚子轴承为研究对象,讨论了滚子分布方式对轴承服役性能的影响,特别指出在调心工况与滚子分布方式联合作用下,球面滚子轴承的动静力学特性,最后能在实验条件有限的情况下设计出实现调心工况的自调心轴承座,为实验验证奠定基础。
(1)交错式滚子分布方式适用于径向载荷较大且调心作用明显的场合;平行式滚子分布方式适用于轴向冲击较大的工作场合。
(2)不论滚子交错分布还是平行分布,主频都约等于单列滚子数与滚子公转频率的乘积。特别的,当球面滚子轴承处于调心工况时,会产生附加频率,频率约等于主频加、减滚子公转频率的整数倍,该结论可用式(28)来表征。
(3)球面滚子轴承的调心功能本身会抵消由于转子挠曲带来的附加弯矩,但调心功能亦会造成滚子偏载。因此,调心作用是以牺牲球面滚子轴承的承载能力为代价的。

