一种自适应形态滤波算法及其在轴承故障诊断中的应用
张西宁,唐春华,周融通,雷威
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
滚动轴承作为旋转机械的基础零部件[1],是现代高效生产链中机械平稳传动、安全运行的关键一环,但同时也常常首先损坏。据统计,在使用滚动轴承的旋转机械中,约有30%的机械故障是由于轴承引起的[2]。当滚动轴承出现局部缺陷时,故障信息会包含在繁杂的振动信号中。由于故障程度、测试条件及噪声干扰等因素的影响,往往难以直接从观测信号中得到反映机械运行状态的有效信息,因此需要借助于快速傅里叶变换(FFT)、小波变换[3]等特征提取方法,尤其是零部件早期微弱故障的检测。
FFT将观测信号的角度转换到频域,信息往往集中在机械结构的固有频率附近,且丢失了时域分辨率。小波变换需要借助人工经验选择小波基,难以自适应地完成。形态学滤波是建立在数学形态学理论基础上的一种非线性滤波方法[4],已广泛应用于医学图像[5]、电力信号[6]及机械故障诊断[7]等领域,其基于信号的几何特征,利用预定义的或与信号成分相适应的结构元素,提取信号边缘轮廓并保持信号主要形态特征,非常适用于分析非线性、非平稳的机械故障振动信号。
Neejarvi等研究了适用于处理一维信号的形态滤波器的频率响应特性[8];Nikolaou等利用膨胀、腐蚀、开运算和闭运算等形态算子对具有周期性冲击特征的信号进行滤波,并认为结构元素长度取0.6倍故障周期长度能达到最优的滤波效果[9]。此外,Patargias等定义并利用形态学指数来预测滚动轴承故障的变化趋势[10];唐贵基和胡爱军等分别研究了开闭、闭开等组合形态算子对于滤波降噪、提高测试信号信噪比的有效性[11-12];章立军等还提出了一种自适应多尺度形态学信号处理方法[13],一定程度上避免了结构元素参数选择的盲目性;鄢小安等借助特征能量因子(FEF)对形态滤波效果进行优化,提出了一种自适应优化尺度组合形态滤波算法[14]。但是,上述针对形态学滤波的研究还存在以下几点问题:①从图像处理引入到机械故障诊断的形态滤波方法,形态算子和结构元素对滤波的影响分析不充分;②对相关机械零部件的故障先验知识依赖较大,自适应性不足;③结构元素参数的选取未结合信号本身特征,对实际轴承故障或早期微弱故障的特征提取效果有限。
因此,本文利用非线性滤波器幅频响应分析法,定量分析了滤波算子和结构元素对滤波的影响。对滚动轴承故障模型和信号分析后,提出一种根据振动信号自身几何特征自适应确定结构元素参数的形态学滤波方法。
1 形态学滤波基本原理
1.1 形态学基本运算
数学形态学诞生于1964年,最初被应用于图像处理领域[15],对应于不同的图像数据格式分别有二值形态运算和灰值形态运算,数学基础分别为集合运算及极值运算。形态变换的基本思想是设计一个作用类似于滤波窗的结构元素,利用其相对原信号做平移匹配,以采集、提取信号中故障冲击特征,进而达到消噪和故障识别的目的。
处理一维振动信号的形态滤波算法可以看作是灰值形态运算的特殊情况,基本运算有4种:腐蚀、膨胀、开算子(op)和闭算子(cl)。设f(n)为原始振动信号,g(m)为一维结构元素,定义域分别为F=(0,1,…,N-1)和G=(0,1,…,M-1),且N≫M,则f(n)关于g(m)的腐蚀、膨胀、开算子、闭算子分别定义为
(fΘg)(n)=min[f(n+m)-g(m)]
(1)
(f⨁g)(n)=max[f(n-m)+g(m)]
(2)
opf(n)=(f∘g)(n)=(fΘg⨁g)(n)
(3)
clf(n)=(f·g)(n)=(f⨁gΘg)(n)
(4)
单独使用腐蚀和膨胀去噪效果有限,所以极少直接用于信号处理。开算子和闭算子能分别平滑掉原信号中的正脉冲和负脉冲,这样便能很好地抑制测试信号中的随机噪声。
1.2 组合形态滤波算子
常用的几种组合形态滤波算子[16]有开-闭算子(FOC)、闭-开算子(FCO)、开闭-闭开组合形态算子(CMF)、形态梯度算子(MG)、形态均值算子(AVG)、白顶帽算子(WTH)、黑顶帽算子(BTH),分别定义如下
FOCf(n)=(f∘g·g)(n)
(5)
FCOf(n)=(f·g∘g)(n)
(6)
CMFf(n)=(FOCf(n)+FCOf(n))/2
(7)
MGf(n)=(f⨁g)(n)-(fΘg)(n)
(8)
AVGf(n)=(f·g+f∘g)(n)/2
(9)
WTHf(n)=f(n)-(f∘g)(n)
(10)
BTHf(n)=(f·g)(n)-f(n)
(11)
形态学基本运算是不可逆的,在信号处理中发挥着不同的作用,通过级联组合方式的变换可以综合利用各自的优势。
以上算子性能各异,配合适当的结构元素,AVG能削弱信号中的高频脉冲;FOC、FCO、CMF能够同时去除正负脉冲,保留信号中的低频、缓变成分;MG、WTH、BTH能消除低频波动而保留部分脉冲峰。为更好地了解各算子的滤波性能,以长度为5的直线型结构元素为例,借助于非线性滤波器频率响应分析法,给出部分组合形态滤波算子的幅频响应曲线。
上述组合形态算子相对于基本形态算子能够满足更丰富的信号滤波需求,但计算效率更低,实际应用时应综合考虑选取。图1中分别展示了带通和高通形态滤波算子的特性。图2为典型低通形态算子幅频特性,从中可以看出,形态闭算子具有良好的低通滤波特性,且计算效率方面具有更大优势。因此,本文选定形态闭算子作为研究对象。
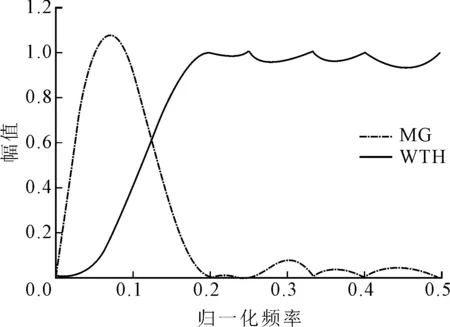
图1 MG、WTH两种形态算子幅频曲线
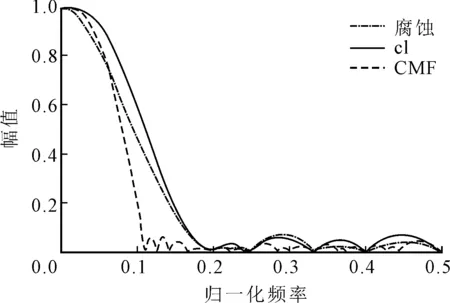
图2 典型低通形态算子幅频曲线
1.3 多尺度形态滤波
由上述分析可知,选定某一结构元素对测试信号进行处理,可以达到保留信号主要特征同时去除大量噪声的目的。但是,当结构元素选择不适当时,例如长度过大,会造成信号波形失真、信息丢失等问题。因而,在某些信号成分比较复杂的情况下,例如零部件存在多点故障源时,可以利用不同尺度的结构元素分别在原信号中搜索相关故障信息,即多尺度形态滤波分析。
以采用直线型结构元素的形态滤波为例,设尺度为i的结构元素记为ig,其中i=1,2,…,Mup,且i和Mup均为正整数,则在此长度范围内的多尺度形态闭运算可用下式表达
(12)
式中:cl(f(n))ig表示选定结构元素ig对信号f(n)进行闭运算;ai为尺度系数,应根据不同尺度下滤波信号反映轴承故障程度的不同而分配,常见的有平均分配法[17]和按滤波后信号与原信号差值大小的权重[18]等指标进行分配。
2 结构元素及其参数
傅里叶变换和小波变换等方法在数学上实质是利用内积变换寻找信号中与基函数相关的成分,以提取动态信号中的故障特征[3]。基于形态算子和结构元素的形态滤波过程与之相似。
形态滤波器由滤波算子和结构元素组成。因而,根据具体滤波需求选定滤波算子后,选取合适的结构元素参数,才能达到理想的去噪效果。
2.1 结构元素形状
形态滤波理论最初应用在图像处理领域,图像可通过一些形状特征描述,所用结构元素往往也会被赋予一定的形状特征,例如利用菱形结构元素可快速获得原始图像骨架。
常用的一维结构元素有直线型、三角型、圆型等,形状由元素的数值分布决定,即其幅值尺度。例如,长度M=5、幅值H=1的直线型和三角型结构元素可分别表示为g=(1,1,1,1,1)、g=(0,0.5,1,0.5,0)。前者能够平滑干扰噪声、保留信号主要特征;后者由于本身包含冲击特征,因而能更多地保留信号中的高频成分。上述两种不同形态滤波器的特性如图3所示。
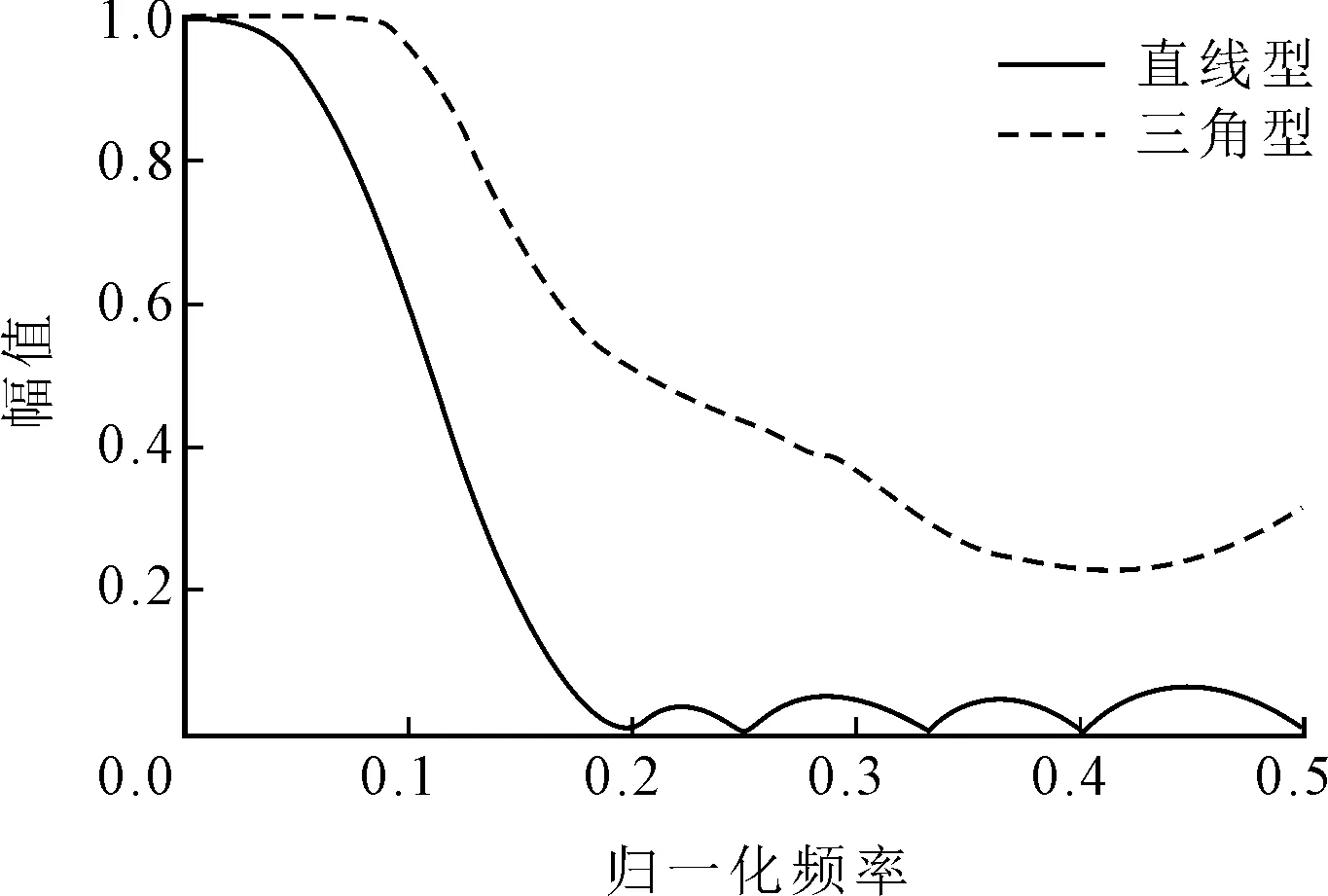
图3 结构元素为直线型和三角型的滤波器幅频特性
2.2 结构元素尺度参数分析
结构元素尺度参数即长度和幅值,两者共同作用影响滤波。大量的数值分析和实验证明,长度的影响更显著,且M越大幅频特性曲线的通带越窄,M越小通带越宽;而幅值H越大,滤波器幅频曲线阻带幅值越大。
由于形态学运算是采取了相加(减)取极值的数值操作,直线型结构元素的幅值尺度对滤波没有影响。因此,在实际运用时可以将幅值尺度取0,以简化算法、提高运算效率。
图4以闭算子为例,给出了直线型结构元素长度尺度变化时的幅频响应关系。当M取较大值时,滤波器通带范围和过渡带都将收窄。表1列出了不同长度值对应的滤波器归一化截止频率,即幅值为0.707时,各幅频曲线对应的频率。

表1 不同长度结构元素对应的截止频率
由于直线型结构元素本身的平滑特性,配合形态闭算子,能够有效提取信号中的主要故障特征信息。在了解基本特性的基础上,结合实际信号特点选定参数,才能提升形态滤波器的综合性能。
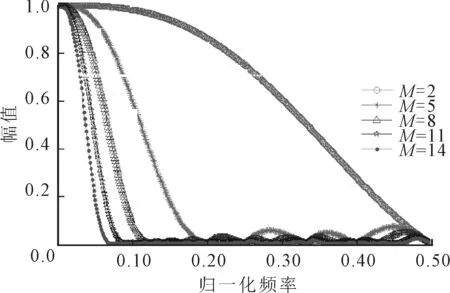
图4 直线型结构元素长度与幅频响应关系
3 自适应形态滤波
3.1 滚动轴承故障特征
文献[19-20]根据滚动轴承出现单点故障时的运动分析,给出了较为普遍适用的故障模型。当滚动轴承由于润滑或安装不正等因素出现疲劳剥落时,旋转件通过故障点会对周围结构产生冲击,信号中呈现出周期性指数衰减高频振荡。理想的外圈故障信号(如图5所示)表达式如下
(13)
式中:fs、N、To、A分别为信号采样频率、采样点数、脉冲重复周期及信号幅值;Sa为和结构阻尼相关的衰减系数;fn为激励起的结构共振频率。
滚动轴承的故障特征主要为低频信息,但测试信号能量往往集中在高频段。为了得到与故障直接相关的低频振动信息,文献[21-22]分别介绍了基于Hilbert变换和Morlet小波变换的解调方法。形态滤波算法非常简洁、高效,是一种非常适用于机械故障信号处理的方法。
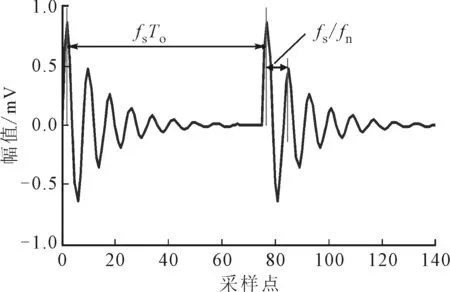
图5 周期性指数衰减高频振荡
3.2 结构元素尺度参数自适应选取策略
形态滤波的自适应实现取决于信号结构元素尺度参数的选取,尤其是M。由于实测信号大多数情况下并不具有明显周期冲击特征,因而文献[9]给出的选取M的经验准则并不适用。另外,基于搜索算法的结构元素优化方法,虽有较好的通用性,但最优参数求解速率使其实际应用受到了限制。
图6截取了实测振动信号中的一段,观察高频振动细节,虽然受到了很大的噪声干扰,但衰减脉冲重复时的高频振荡频率几乎没有改变。因而,结构元素的长度取为两次高频振动的峰值间隔点数或一个故障周期对应的采样点数都是合理的,即
fs/fn≤M≤fsTo
(14)
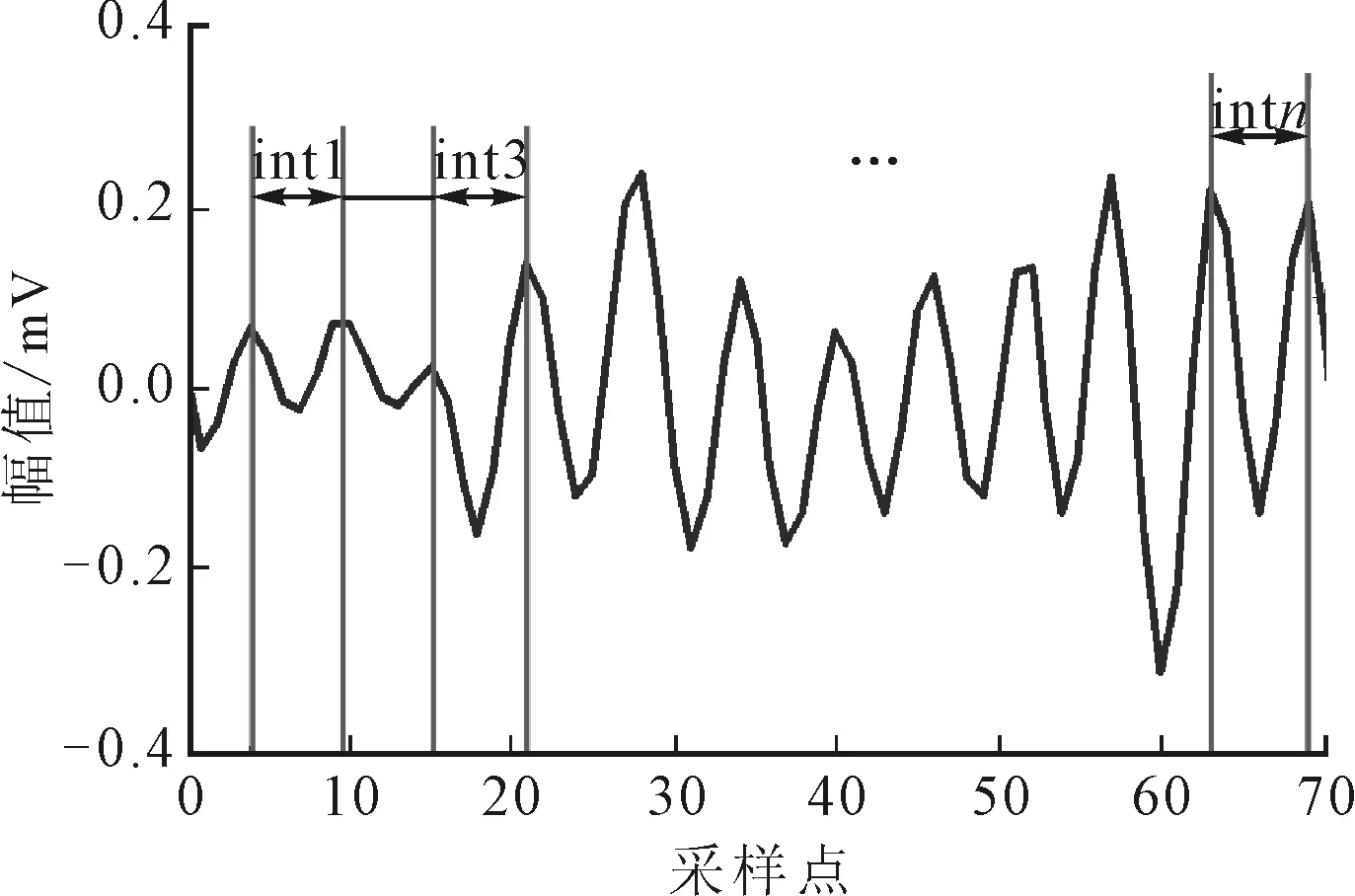
图6 局部峰值间隔采样点
参数M可借助共振解调带通滤波器中心频率的确定方法而定,包括快速谱峭度图[23]或者基于小波熵的参数寻优等。但是,这些方法由于指标的局限性及算法的复杂性,不利于故障信号的实时处理。
这里利用少量原始信号采样点寻找局部峰值,再计算间隔采样点数的方法,确定M
M=rmax[int1,int2,int3,…,intn]
(15)
式中:r为修正因子,一般取1~3,本文分析时取为1;同时利用80~100个采样点便可估算出较准确的fs/fn,本文分析时取为100。
3.3 数值仿真实验
利用形态闭算子和直线结构元素对图5所示信号进行滤波,取M=fs/fn=7,结果如图7所示。
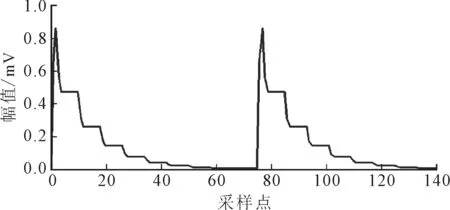
图7 自适应闭算子滤波结果
实验结果验证了根据上述策略选定直线结构元素对机械故障信号进行自适应滤波的可行性。即使实测的轴承内圈或滚动体故障信号中存在复杂的调制现象以及其他干扰噪声,但信号中的高频共振细节成分总能保留下来一部分。因而,所提方法在实际应用中具有可推广性。
4 实验信号分析
4.1 方法验证
为验证上述分析,用凯斯西储大学轴承数据中心的实验信号进行分析。实验所用轴承型号为6205-2RS_JEM_SKF,内圈、外圈、滚动体(9个)和节圆直径分别为25、52、7.94、39.04 mm,接触角为0°。局部故障通过电火花加工在外圈和内圈滚道表面中间的凹坑,直径为0.533 4 mm、深度为0.279 4 mm;外圈故障信号在故障点位于载荷区对面的条件下测试得到的。实验转速为1 772 r/min,内、外圈故障特征频率分别为159.93、105.87 Hz。采样频率为12 kHz,数据时长为0.5 s。
从外圈故障振动信号时域波形中可以看到较为明显的冲击,但在相应信号频谱中却得不到足够与故障直接相关的信息,如图8~图11所示。
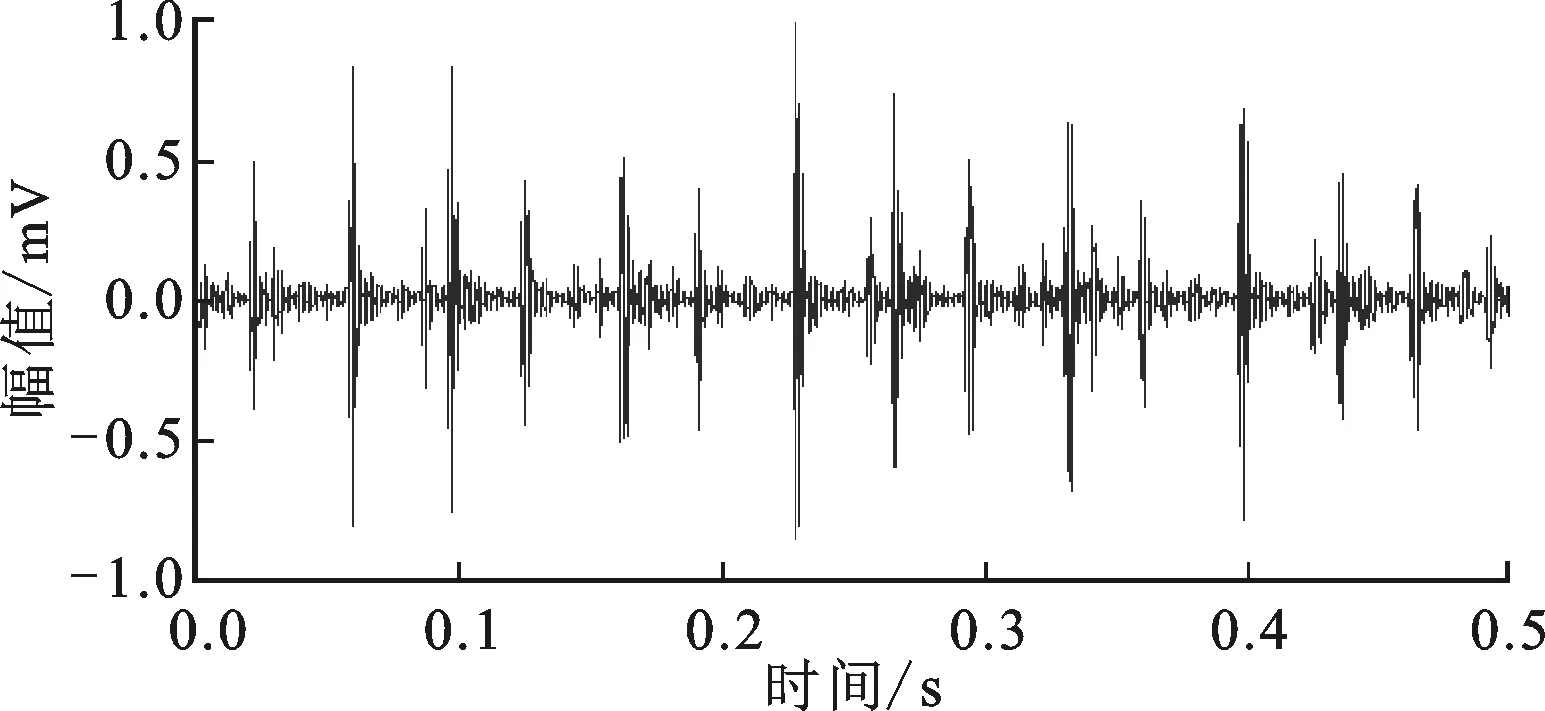
图8 外圈故障振动信号
文献[15]提出了基于FEF的参数优化形态滤波方法,并取得了比采用信噪比最大化准则进行形态滤波更好的效果。用本文方法提取滚动轴承故障特征,并与之对比,可验证本文方法的实用价值。
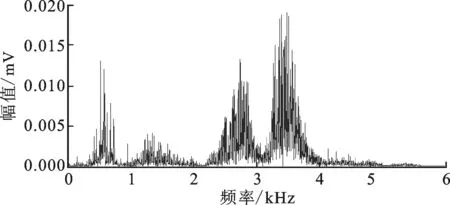
图9 外圈故障信号频谱
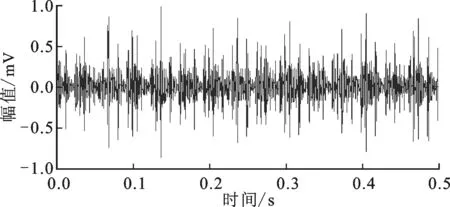
图10 内圈故障信号
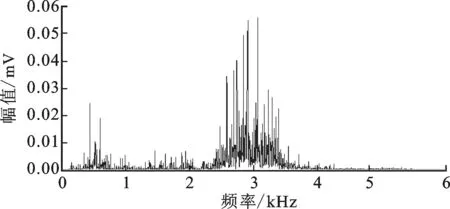
图11 内圈故障信号频谱
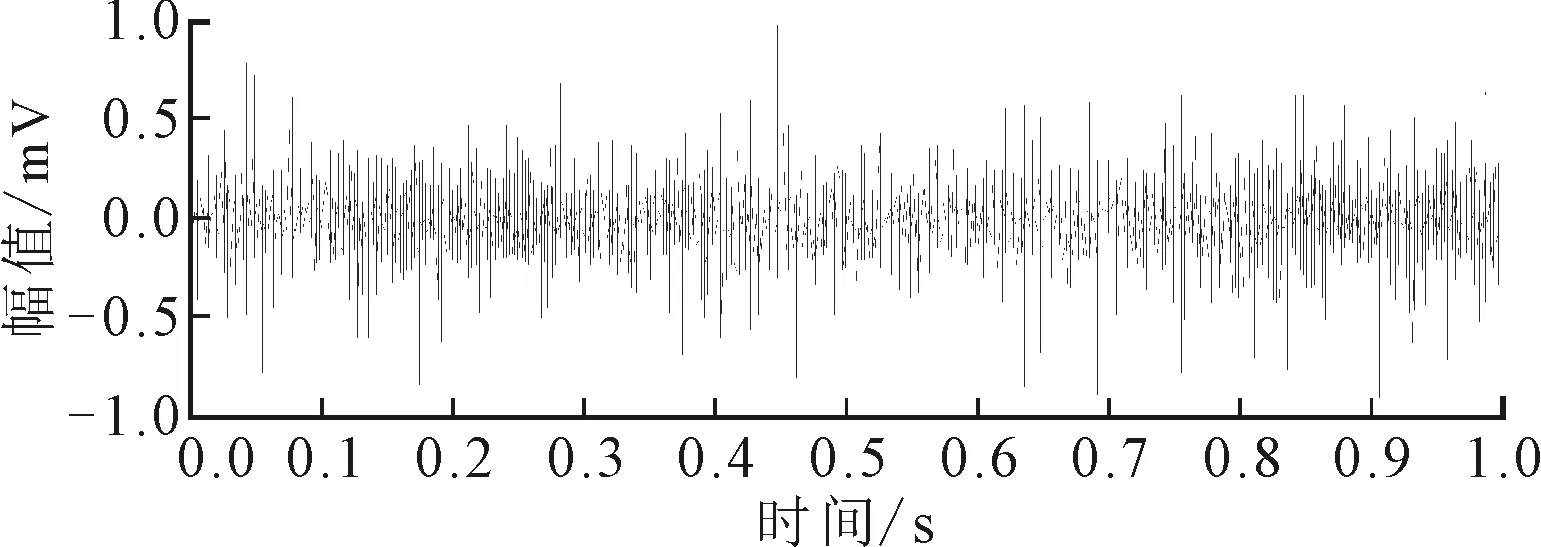
运用所提自适应结构元尺度选取方法时,在振动信号采集初期便可计算得到信号对应的理想的M,有利于开展实时故障诊断。外圈故障信号经闭算子滤波后,故障特征被很好地揭示了出来,如图12所示。
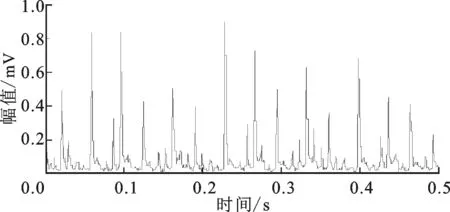
图12 外圈故障信号自适应形态滤波(M=5)
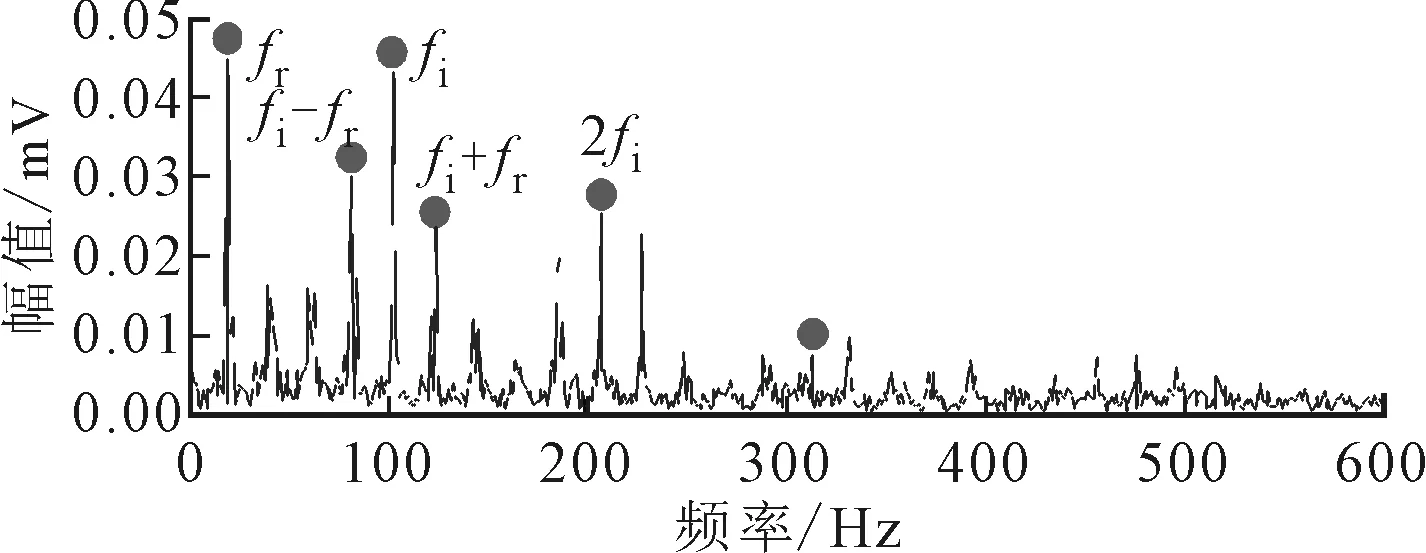
图13中,存在连续的外圈故障特征频率fo及其谐频成分,还有以转频fr为间隔的边频分量。
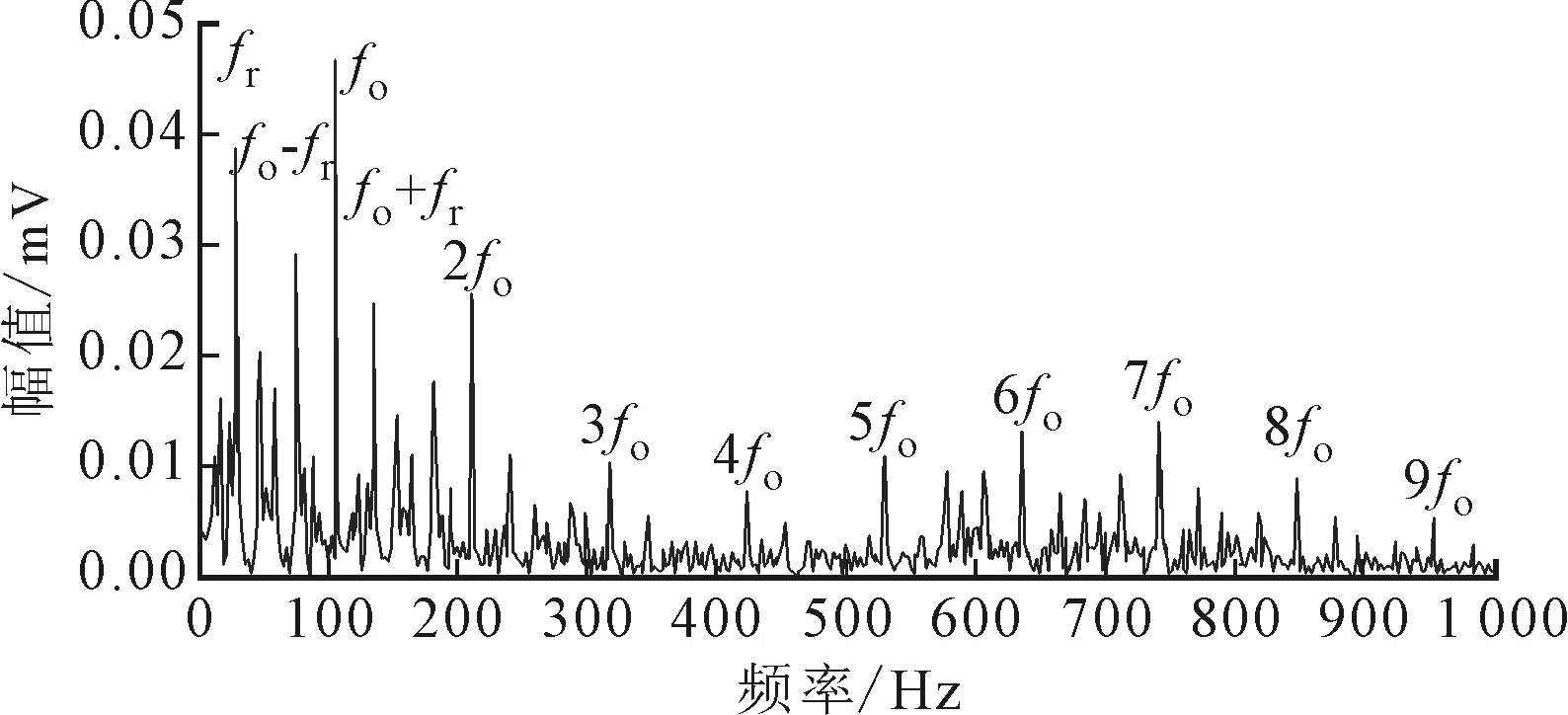
图13 外圈故障信号自适应形态滤波频谱
以FEF指标最大为最优CMFH滤波效果的目标,得到的优化结构元素长度Mop=17,滤波结果如图14所示。其中CMFH即原信号与CMF滤波信号的差值,该形态算子具有高通滤波特性。FEF即信号包络谱图中故障特征及其谐频成分占频谱总能量的百分比。将FEF提取对象从包络谱转换为频谱,称为特征幅值能量比(FAER)。
图14 外圈故障CMFH滤波信号(Mop=17)
图15中虽然出现了一些外圈故障信息,但噪声干扰依然很大,外圈故障特征频率对应的谱线并不明显。借助于Hilbert变换得到包络谱,诊断效果有所提升,如图16所示。
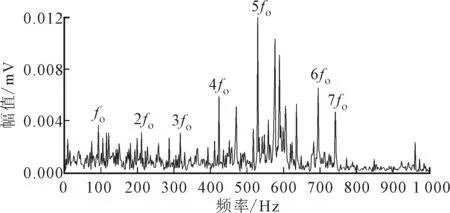
图15 外圈故障CMFH滤波信号频谱
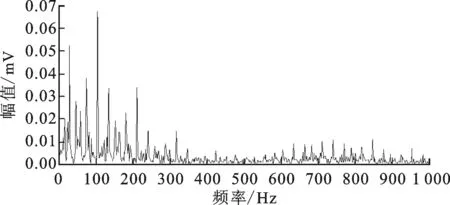
图16 外圈故障CMFH滤波信号Hilbert包络谱
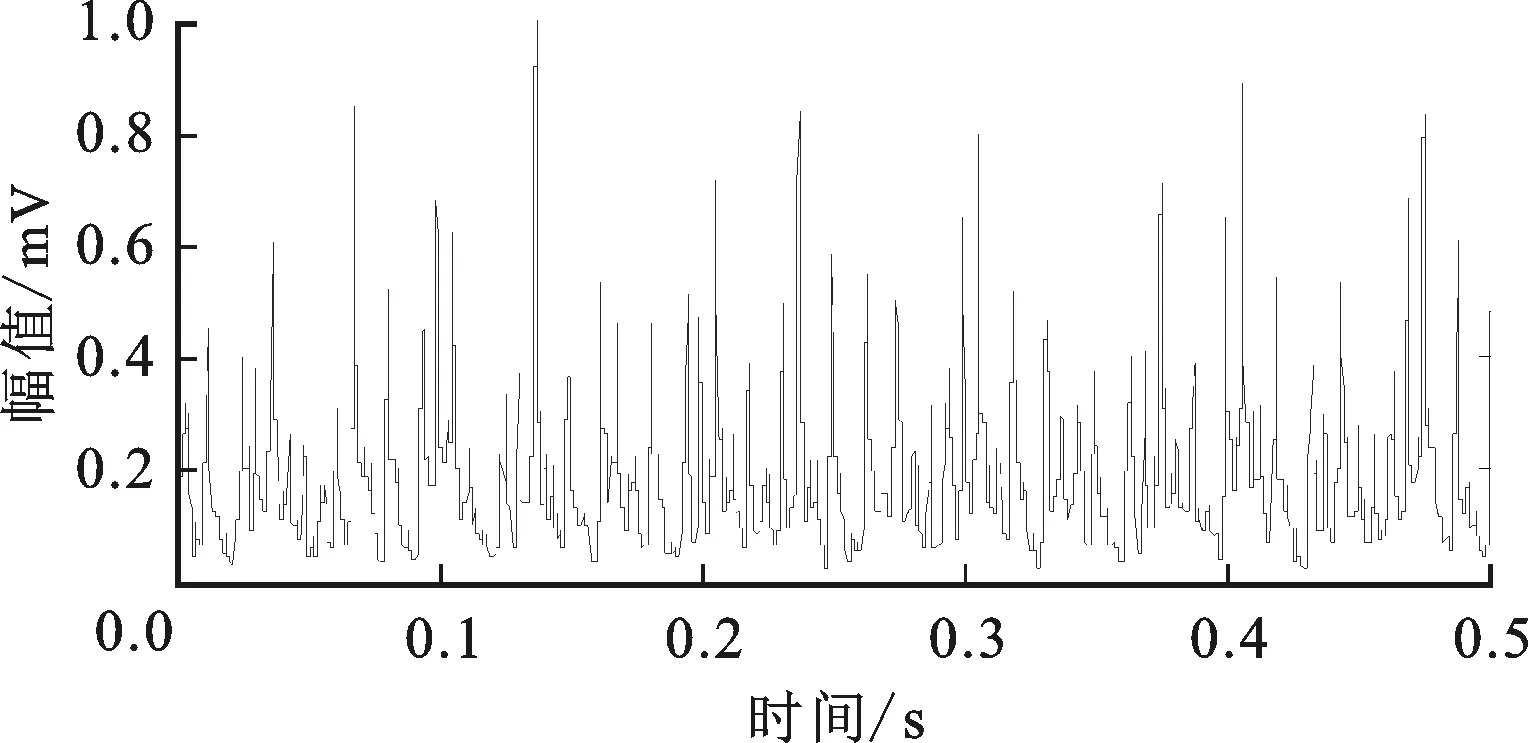
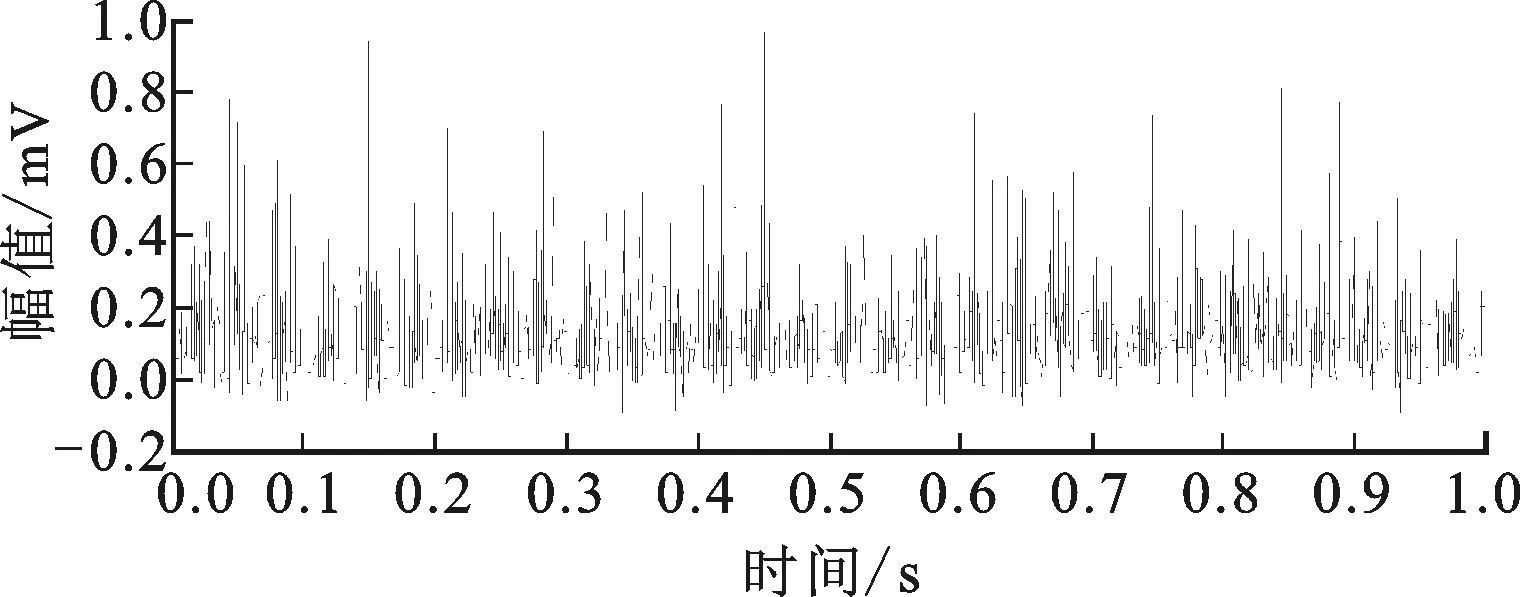
图17 内圈故障信号自适应形态滤波(M=5)
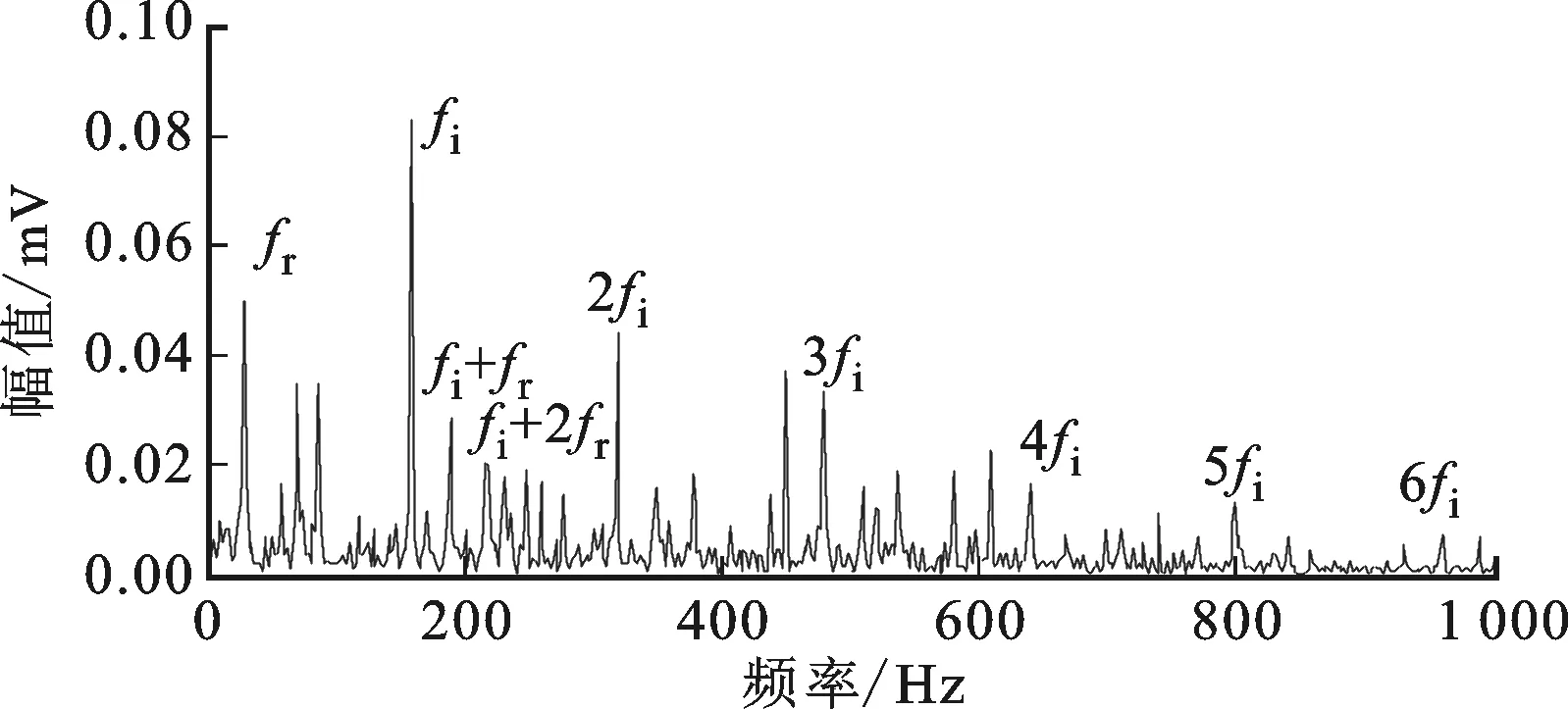
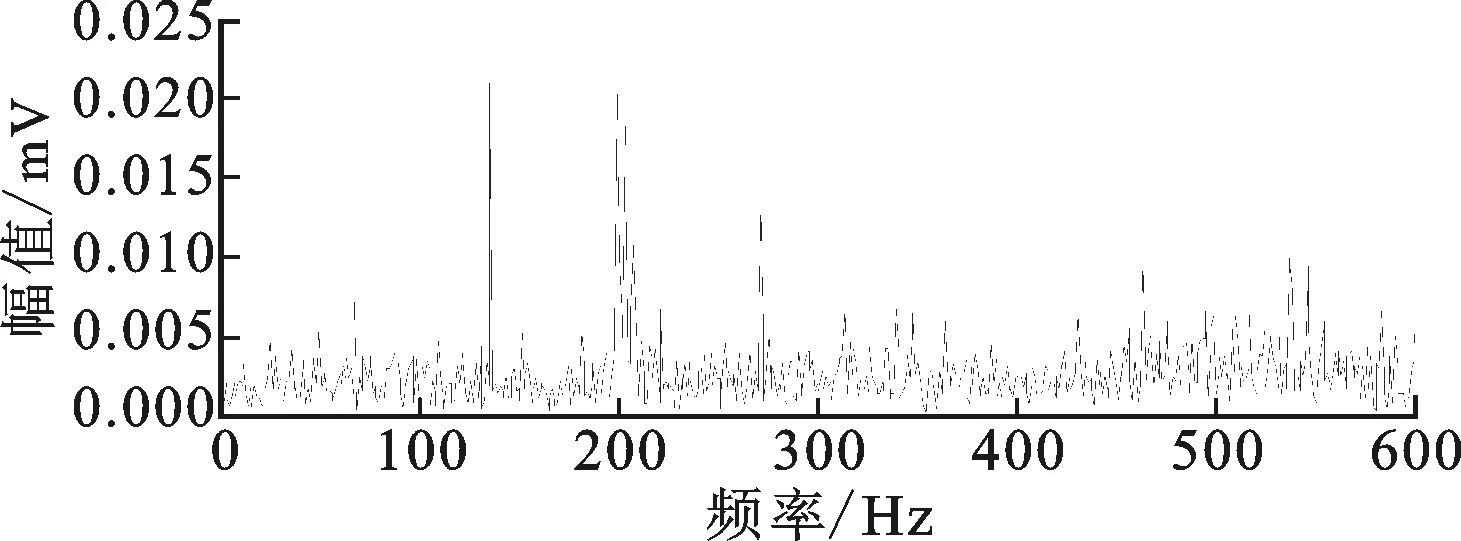
图18 内圈故障信号自适应形态滤波频谱
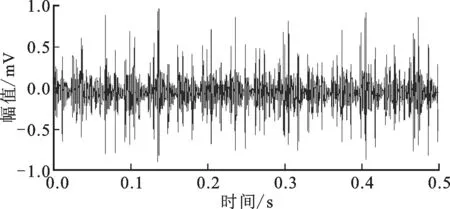
图19 内圈故障CMFH滤波信号(Mop=17)
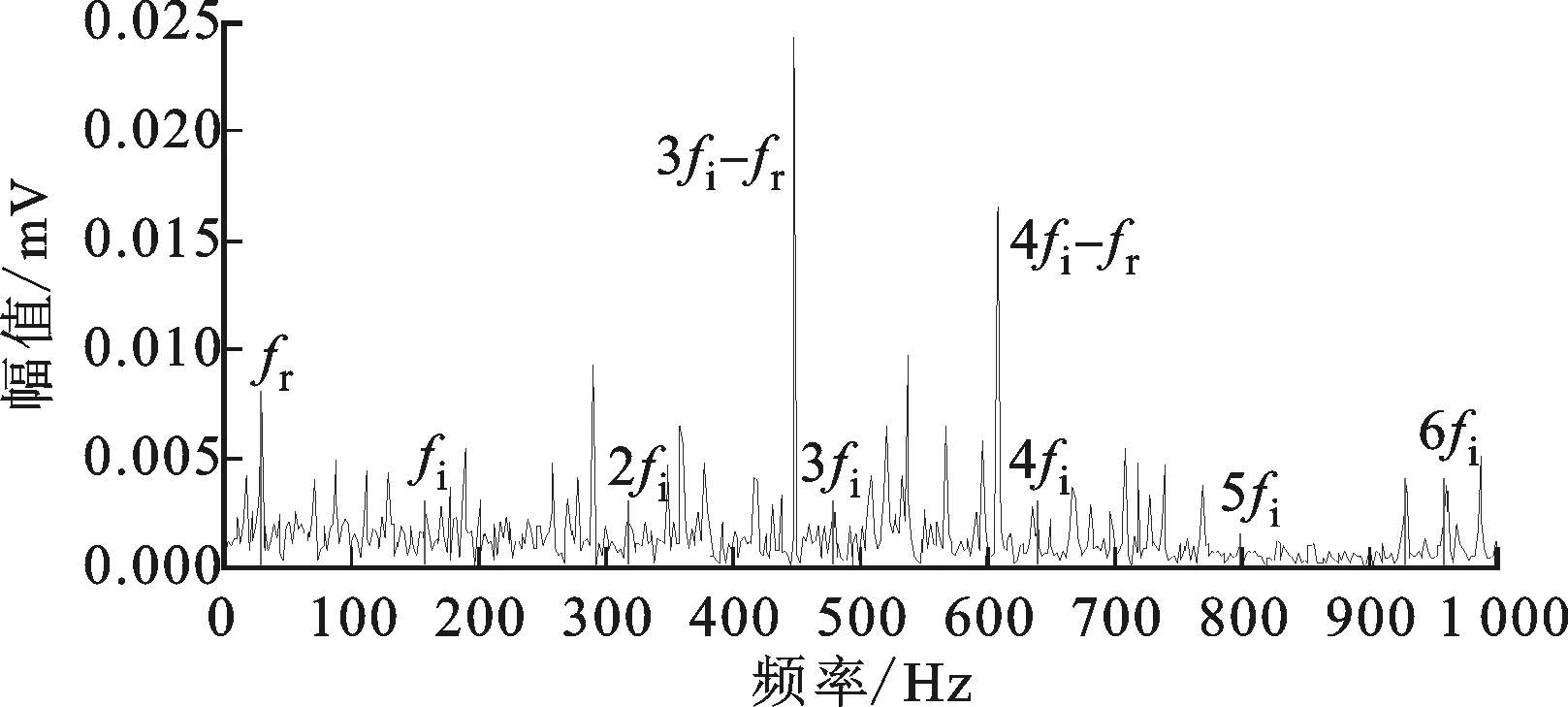
图20 内圈故障CMFH滤波信号频谱
图17和图18展示了本文所提方法在内圈故障信号处理中的应用效果,得到了清晰、明确的内圈故障信息,效果甚至优于图19~图21的滤波结果,其中fi为内圈故障特征频率。
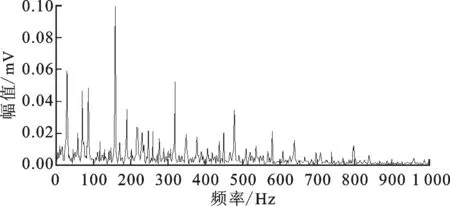
图21 内圈故障CMFH滤波信号Hilbert包络谱
在上述实验分析中,外圈信号经本文方法、优化CMFH两种方法得到的信号FAER指数分别为0.232 5、0.179 1,提高了29.8%;内圈信号处理后,两者分别为0.329 9、0.011,明显加强了故障特征。此外,本文方法处理内圈信号用时2.6 ms,CMFH配合Hilbert解调算法用时5.2 ms(还需多次运行),算法效率至少提高了50%。经过多次实验分析,本文方法均可提高滚动轴承故障诊断的效果及算法效率,说明在机械故障诊断中极具实用性。
4.2 滚动轴承故障诊断实验
为进一步证明本文方法的可靠性,开展了滚动轴承故障诊断实验。局部故障通过激光在外圈和内圈的滚道表面中间以及滚动体表面分别加工了面积约为7、3.8、7 mm2的凹坑,深约为0.1 mm。
实验台见图22,所用传感器为IMI 601A11加速度计,信号采样频率为10 kHz,采样持续1 s。轴承内圈实验转速约为1 305 r/min,外圈、内圈、滚动体故障特征频率分别为67.1、107.6、90.2 Hz。外圈故障较容易检测,下面仅给出内圈和滚动体信号处理的结果。

图22 滚动轴承实验台
图23中的周期性脉冲并非源于内圈故障,是与内圈配合的轴产生了一定弯曲造成的。
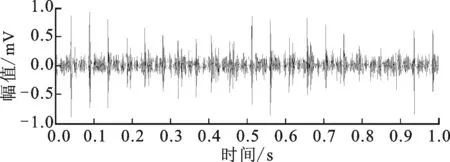
(a)原始信号
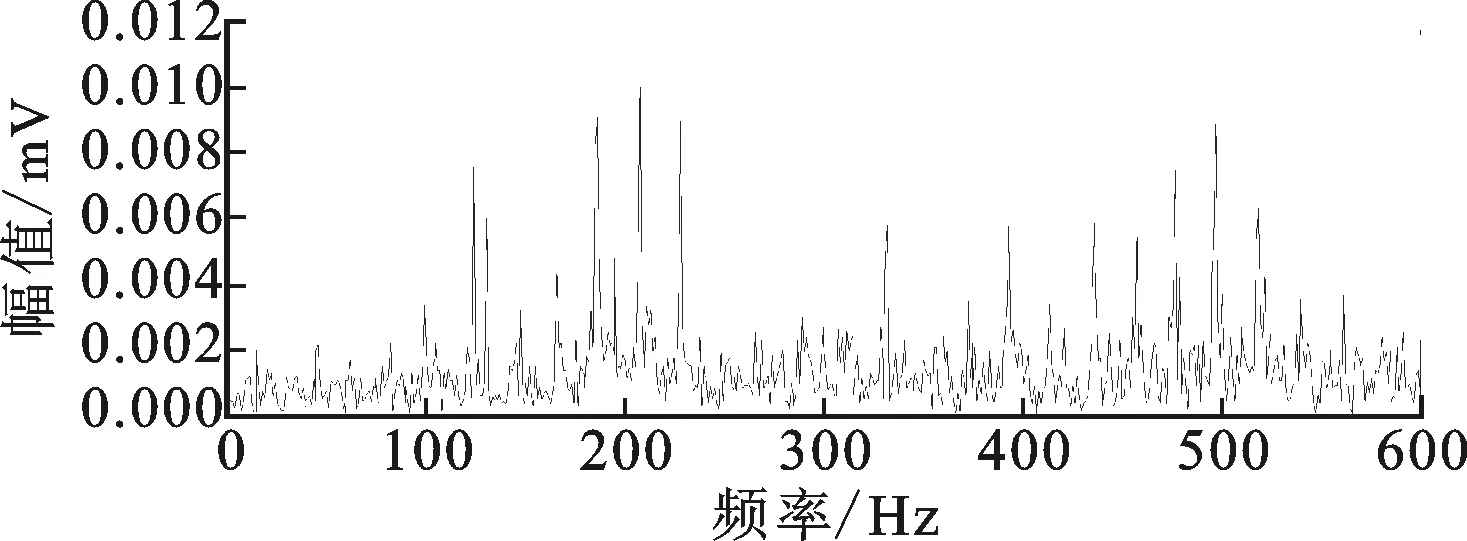
(b)原始信号频谱
图24表明本文方法能够抑制非轴承因素干扰,突出内圈故障特征,这得益于形态学滤波十分优良的非线性特征提取能力。
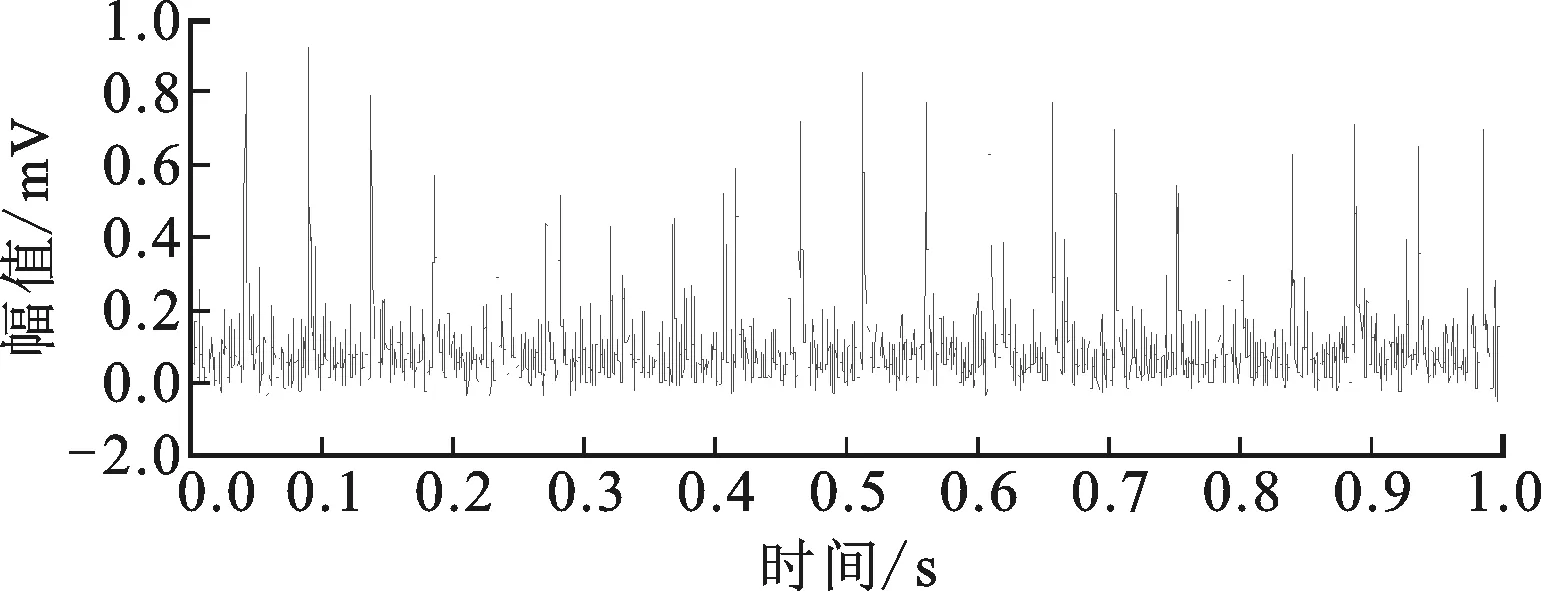
(a)时域信号
(b)频谱图
(a)原始信号
(b)原始信号频谱
(a)原始信号
(b)频谱图
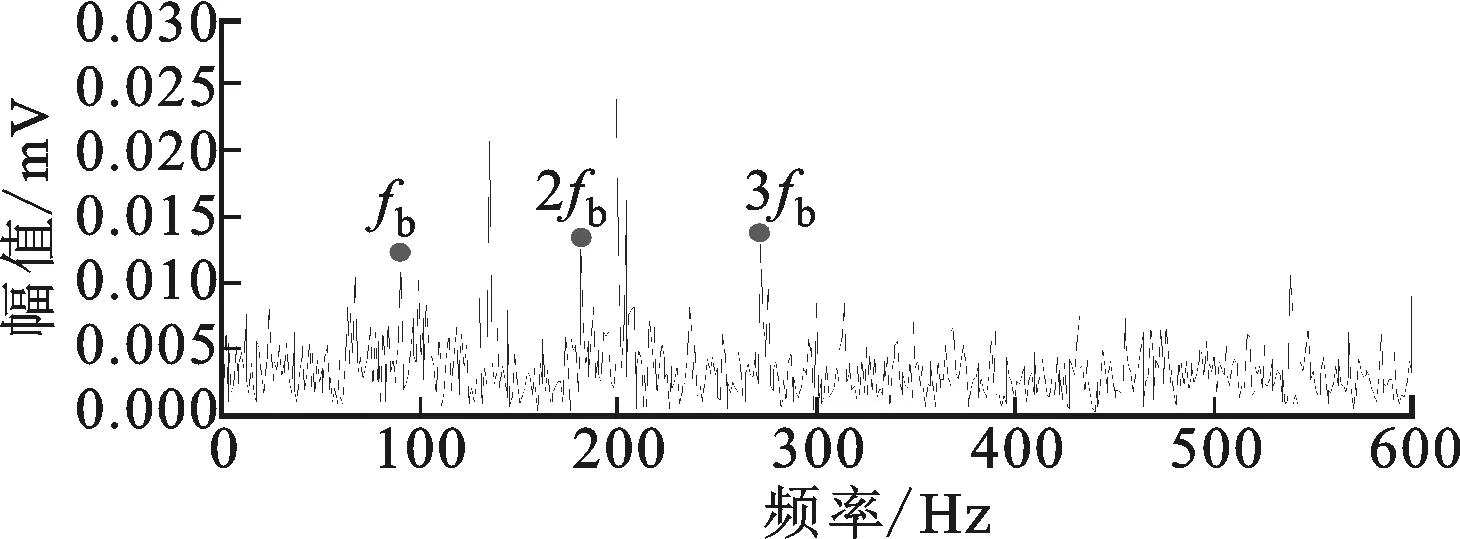
滚动轴承运动复杂,故障不易发现,原始信号见图25。但本文方法从繁杂的原始信号中,找到了滚动体存在一定程度故障的相关信息,如图26所示,其中fb为滚动体故障特征频率。
以上实验分析结果进一步证明了本文方法的有效性和稳定性,表明在机械故障诊断信号处理中的良好应用前景。
5 结 论
本文利用非线性滤波器幅频响应分析法,总结了各形态算子的滤波特性,分析了结构元素长度尺度及幅值尺度在滤波过程中发挥的作用,进而提出一种新的自适应形态滤波算法。利用信号局部细节特征选取最佳直线结构元素长度尺度,与形态闭算子组成一种适用于振动信号处理的形态滤波器。在滚动轴承故障诊断实验中,本文方法与其他基于形态滤波的方法相比,诊断准确性和运算效率均有较大提升。
(1)形态滤波在机械故障诊断中的应用取决于形态算子的类别和结构元素参数,选取时应综合考虑滤波性能和运算效率;
(2)滚动轴承典型故障信号常伴随大量噪声和调制现象,但周期性冲击激励起的结构固有振动的细节信息总能保留下来一部分;
(3)基于形态滤波的信号处理算法类似于匹配滤波过程,自适应实现取决于结构元素尺度的选取:直线结构元素能起到平滑消噪的作用,且算法效率最高;三角结构元素能较多地保留原信号中的高频振动、拓宽形态滤波器的通带范围。
(4)本文方法的关键在于直接利用测试信号的局部细节特征,为了能更有效地解决实际工程问题,考虑滚动轴承润滑、各元件动力学性能等因素是未来工作的重要研究方向。

