智能旋翼振动高阶谐波控制方法

邓旭东,胡和平,孟 微

(中国直升机设计研究所 旋翼动力学重点实验室，江西 景德镇 333001)

0 引言

直升机旋翼工作在复杂的非定常气流环境中，前行侧激波、后行侧失速以及桨涡干扰等因素导致旋翼振动问题突出。振动载荷经旋翼轴传递引起机体振动，因此针对旋翼的控制是解决直升机振动问题的治本方法。智能旋翼采用智能材料作动器对桨叶整体或局部气动面进行驱动，由此产生能够抵消桨叶自身振动的附加气动载荷。智能旋翼有主动扭转桨叶(ATR)、主动格尼襟翼(AGF)以及主动后缘襟翼(ACF)等多种构型，其中ACF构型最具工程应用潜力，研究表明，采用恰当的控制方法，能有效抑制旋翼振动载荷。

针对智能旋翼振动控制方法，欧美国家开展了广泛而深入的研究，大致可分为时域控制与频率控制两类。具有代表性的时域控制方法有基于线性系统的H∞方法[7-8]、基于状态空间或传递函数模型的连续时间高阶谐波控制方法(CTHHC)[4-6]以及神经网络控制方法[3]。值得一提的是，欧直公司采用带自抗扰能力的H∞控制器，分别在2006年与2009年对换装ACF智能旋翼的EC145直升机进行了飞行验证，结果表明施加主动控制后驾驶员座椅处的垂向振动降低到0.05g以下；MIT联合波音公司采用基于传递函数模型的CTHHC方法，对带后缘襟翼的SMART旋翼进行了闭环控制风洞试验，桨毂垂向振动载荷最大降幅可达80%。以上两项研究基本代表了欧洲与美国在该领域的标志性成果。频域控制方面，以美国高校为主的研究人员针对基于准静态传递矩阵的高阶谐波控制开展了一系列理论与模型试验研究[14-17]，结果表明在稳态飞行条件下，频域方法对旋翼振动载荷有出色的控制效果。相比时域控制，频率方法对计算资源要求更低，更易于实现。

在国内，智能旋翼振动控制研究起步较晚，主要进行了一系列理论跟踪与半物理试验工作。李春明[12]，夏品奇[13]分别采用神经网络控制器与最优控制方法对ACF智能旋翼振动控制进行了理论分析。

本文以ACF智能旋翼为对象，结合广义卡曼滤波识别算法与目标函数最优控制理论，构建了一种具有传递矩阵在线识别能力的频域高阶谐波控制方法。在此基础上进行了闭环控制仿真，对参数影响与控制算法的鲁棒性进行了分析，验证了文中方法的有效性，同时得出了若干定性结论，可用于指导智能旋翼振动控制试验。

1 高阶谐波控制算法

对于N片桨叶的旋翼而言，桨毂振动载荷以频率为NΩ的谐波量为主，由频率为(N-1)Ω，NΩ以及(N+1)Ω的桨叶载荷集成得到(Ω为旋翼转速)。因此ACF智能旋翼高阶谐波控制的基本思路是通过对襟翼(N-1)Ω，NΩ以及(N+1)Ω谐波偏转角的控制来抑制桨毂NΩ的振动载荷，控制流程如图1。

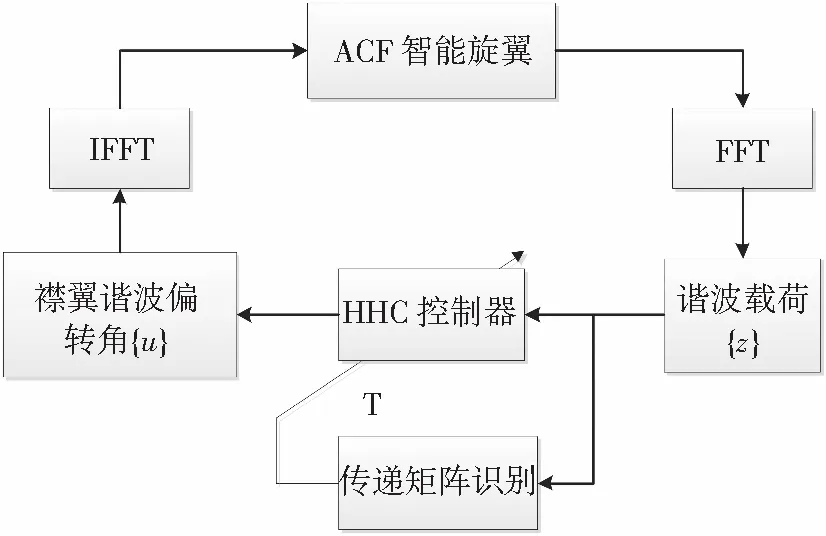
图1 ACF智能旋翼高阶谐波控制流程

其中传递矩阵识别与HHC控制算法是关键环节，其设计好坏直接影响振动载荷控制效果。u，z分别代表襟翼谐波偏转角与旋翼谐波载荷的列向量，可表示为：

(1)

下标c，s分别代表余弦项和正弦项，N，N-1，N+1为频率阶次。考虑到桨毂载荷时域量FFT运算需要，通常令旋翼每旋转整数倍圈更新一次u，传递矩阵T同步更新。

1.1 传递矩阵识别算法

ACF智能旋翼的传递矩阵模型建立在襟翼谐波偏转角与桨毂谐波载荷之间的线性假设上，即：

(2)

其中下标k代表第k组样本，一组样本包含一个输入列向量u和与之对应的输出列向量z，可通过实测或计算得到。定义输入、输出样本的增量矩阵为：

(3)

对于本文而言，Θ，Z，T分别为6×ns，12×ns，12×6矩阵，ns为识别所需的样本数量。

传递矩阵T的识别采用广义卡曼滤波方法，通过寻找T的最优解，使形如下式的性能指标函数JID达到极小值。

(4)

式中T*表示T的预估值；R，M分别为Z-TΘ，T-T*的协方差矩阵；下标i代表矩阵的第i行。当JID达到极小值时，有：

(5)

由式(4)、(5)可得：

TiΘRi-1ΘT-ZiRi-1ΘT-Ti*Mi-1+TiMi-1=0

由此可得到Ti的计算式：

(6)

将式(6)拓展到所有行：

(7)

T*可用上一步的T值代替，因此式(7)可视为传递矩阵的递归计算公式。

初始传递矩阵T0可通过预采集一定数量的样本，利用数值微分法计算。矩阵R、M关系到识别精度，须预先设定，简单起见可令R、M分别为对角阵，且各自的对角元素相等。通常广义卡曼滤波识别效果同M与R对角元素之比直接相关，只需调整M/R即可对算法进行调谐。

1.2 振动控制算法

智能旋翼振动载荷高阶谐波控制采用线性最优控制器，通过最小化目标函数Obj来给出相应的襟翼偏角输入。

Obj=zkTWzzk+ukTWuuk+ΔukTWΔuΔuk

(8)

Wz，Wu，WΔu分别为输出载荷、输入偏角以及偏角增量所对应的权重矩阵，均为对角阵。当目标函数达到极小值时，∂Obj/∂uk=0，可得最优控制输入为：

uk+1=(DkWΔu+DkTkTWzTk)uk-DkTkTWzzk

Dk=(TkTWzTk+WΔu+Wu)-1

(9)

下标k代表第k个控制步，每一步的控制输入u与传递矩阵、权重矩阵以及上一步的输入有关。

为调节控制量更新幅度，避免目标函数在控制过程中出现过大振荡，引入修正系数α，即：

(10)

该控制算法性能依赖对权重矩阵与修正系数的调节，权重矩阵可采用如下设定方法：

(11)

式中系数βz，βu，βΔu用来设定向量z，u，Δu在目标函数中的占比，对角阵wz，wu，wΔu可调整向量中各元素之间的相对重要程度。对于ACF智能旋翼振动控制来讲，主要目的是降低载荷向量z，但受限于襟翼运动能力，必须令u保持小角度，为保证相邻两步控制信号的连续性，还应使Δu尽量小。

2 算例与分析

以某4桨叶铰接式ACF智能旋翼为例，分别从传递矩阵识别与振动载荷闭环控制仿真两方面对本文所提出的高阶谐波控制方法进行验证。算例旋翼桨叶如图2。

图2 ACF智能旋翼桨叶

基本参数如表1。

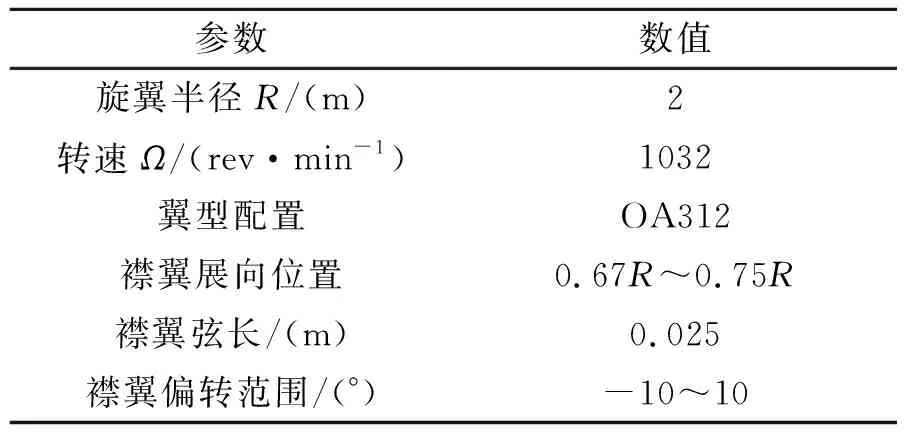
表1 算例旋翼基本参数

给定偏角输入u，对应的旋翼振动载荷输出z采用CAMRAD II计算得到，该软件是一款成熟的直升机综合分析软件，已得到行业内的广泛认可。所有计算均在旋翼前飞配平状态下完成。

2.1 传递矩阵识别精度

令襟翼偏角输入向量u的每个元素为-2.4°～2.4°之间的随机量，在这种条件下计算70组输入向量u对应的输出z，并在每个输入点处利用向前差分法计算z相对于u的雅克比矩阵TJ。

由于输入、输出数值上存在明显的量级差异，为保证矩阵运算数值的稳定性，利用0偏角输入下的载荷向量的绝对值abs(z0)作为输出向量z的比例因子，输入向量u的比例因子为2.4°，得到的70组输入-输出样本用于传递矩阵识别，对应的雅克比矩阵可视为传递矩阵的确切值，定义识别误差为：

(12)

令ns=6，M/R=0.001、0.01、0.05，样本识别误差分布如图3。

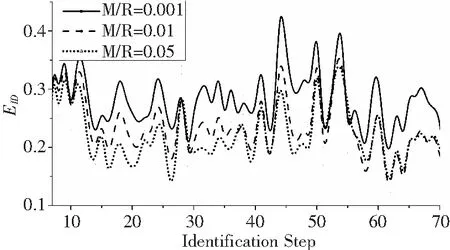
图3 识别误差分布(不同M/R)

由于识别运算需要ns个样本，识别从第ns+1个样本开始。图中可见，识别误差处于0.1～0.5之间，随着M/R增大，误差逐步减小。

令M/R=0.05，ns=2、6、10，样本识别误差分布如图4。

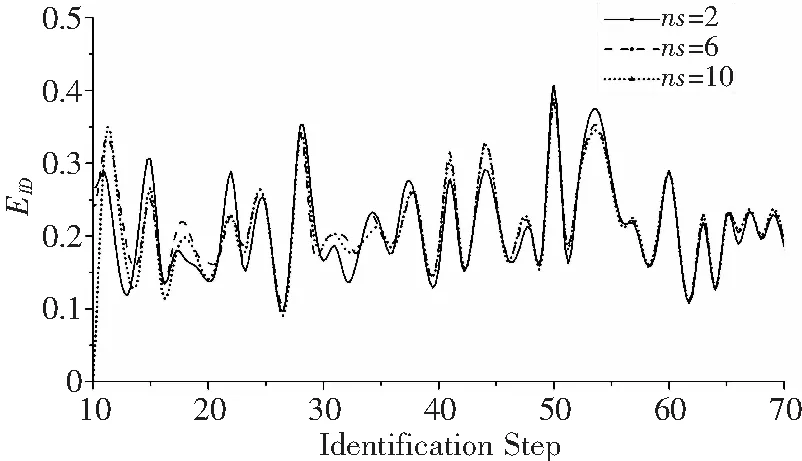
图4 识别误差分布(不同ns)

图4表明样本个数对识别精度影响不明显，随着识别步数增加，三条误差曲线基本重合，因此仅增加样本数量并不能提高识别精度。

2.2 振动载荷闭环控制仿真

2.2.1 特定状态控制效果

采用带传递矩阵在线识别的高阶谐波方法对ACF智能旋翼进行振动载荷闭环控制仿真，旋翼工作状态及算法参数如表2、表3所示。

表2 算例旋翼工作状态

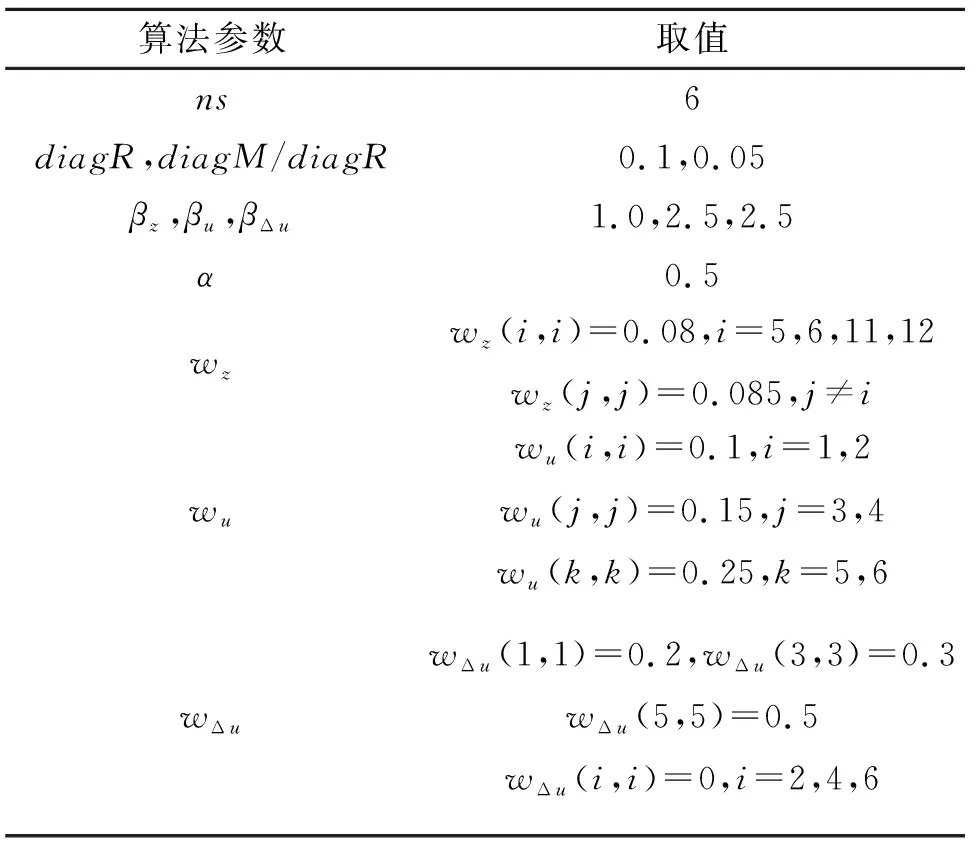
表3 控制算法参数

将基准状态(0偏角输入)下的振动载荷向量z0作为因子，定义目标函数的相对量：

Objr=Obj/(z0T·Wz·z0)

控制流程从0偏角输入开始，目标函数的迭代过程如图5。

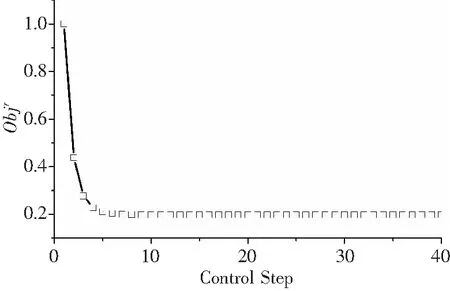
图5 目标函数控制过程

由图5可见，经过8次控制更新，目标函数约降低80%，随后趋于平稳，实现最优控制。

图6给出了算例旋翼基准状态与最优控制状态下，固定坐标系中4Ω无量纲桨毂载荷的对比。可见，三个方向上的旋翼振动载荷控制效果明显，航向力F4x与侧向力F4y的降幅超过40%；滚转力矩M4x，俯仰力矩M4y以及垂向力F4z降幅在90%以上，扭转力矩M4z的降幅也接近80%。

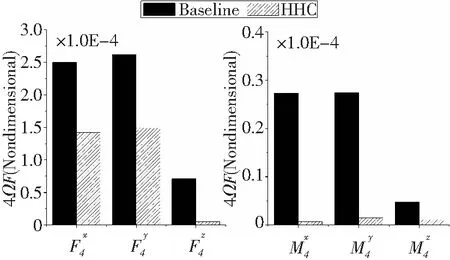
图6 4Ω桨毂载荷控制效果

襟翼偏角向量u的更新过程如图7所示， 6个分量在整个控制过程中均保持较小角度，连续性较好。

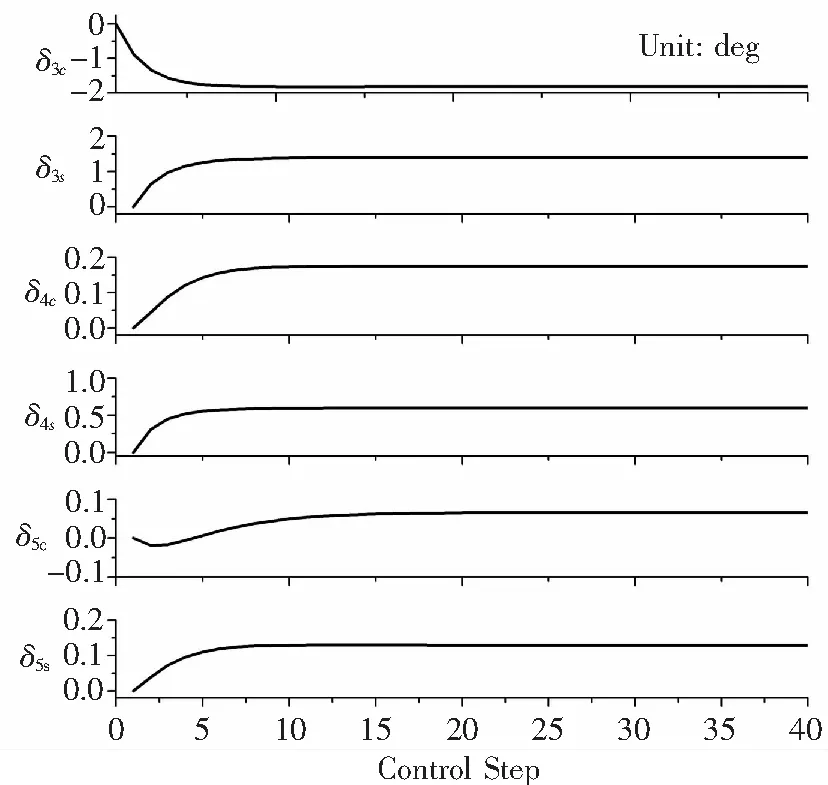
图7 襟翼偏角输入更新过程

2.2.2 权重矩阵影响

令前进比为μ=0.25，按照式(12)给出的权重矩阵设置方法，βz=1，分别令βu=βΔu=1、2、3 ，其他状态与算法参数与表2、表3一致。目标函数迭代过程见图8。

达到最优控制状态后，无量纲4Ω桨毂载荷与襟翼偏转角的时域量如图9、图10。

可见βu，βΔu越大，目标函数的降幅越小，控制器对旋翼振动载荷的控制能力越弱，这是由于襟翼偏角u及其增量Δu在目标函数中的比重升高，导致振动载荷z的比重降低，从而使其控制幅度减小。另一方面，βu，βΔu增大也降低了最优控制所需的襟翼偏角。

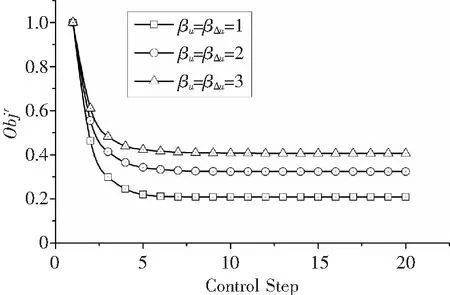
图8 权重系数对目标函数的影响

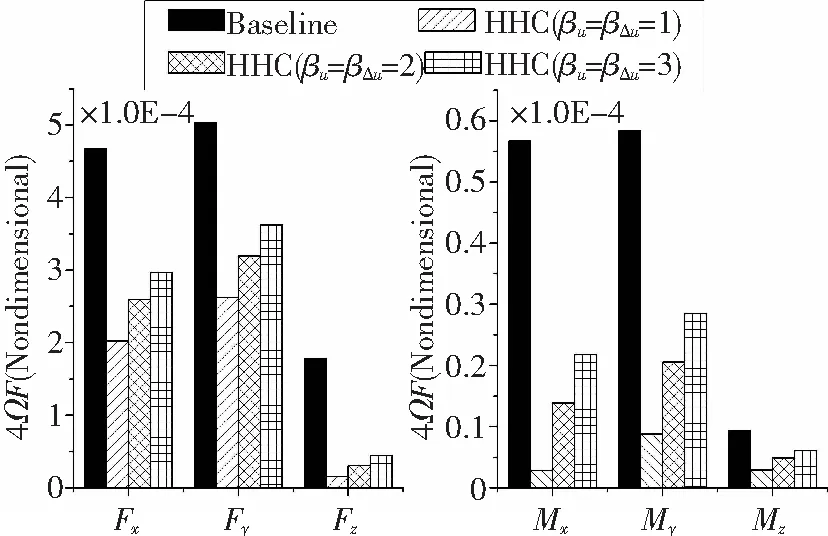
图9 4Ω桨毂载荷控制效果对比

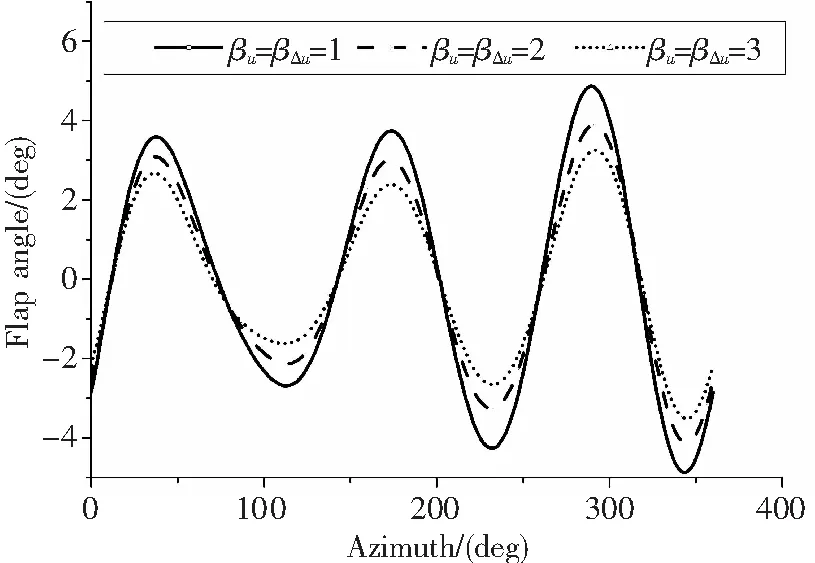
图10 襟翼偏角对比

2.2.3 鲁棒性验证

为验证控制器对旋翼工况变化的应对能力，采用表3给出的控制参数进行80步闭环仿真。控制以表2状态为起始，并在进程中对旋翼工况依次进行如下改变：

1)第15步将μ提高到0.25；

2)第30步将CL/σ提高到0.08；

3)第45步恢复到初始状态。

目标函数的变化历程如图11。

图中可见，在第15、30、45控制步，目标函数有较大的波动，这是由于旋翼飞行状态改变，导致输入u到输出z的传递关系发生较大变化，在线识别样本中还包含上一状态的u和z，无法准确识别T。随着控制步增加，当前状态的输入、输出数据逐渐填补进来，T的识别精度提高，目标函数得到了有效控制。第45步时旋翼恢复初始状态，目标函数的控制水平随即恢复。

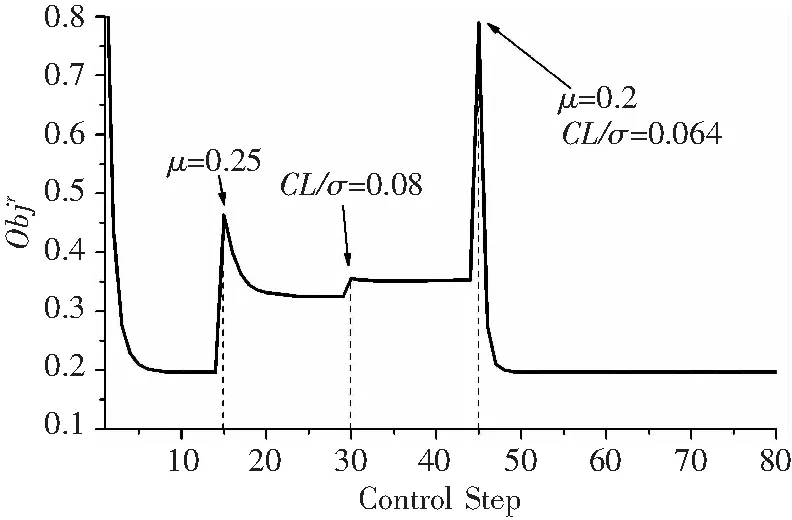
图11 目标函数控制过程(变状态)

为研究控制过程中4Ω旋翼振动载荷的变化规律，定义振动载荷相对量如下：

z0为对应状态的基准载荷(0偏角输入)，F4xr、F4yr、F4zr、M4xr、M4yr、M4zr的变化情况如图12。

在各工况下重新达到最优控制状态后，控制器对旋翼振动载荷的控制能力产生了不同程度的变化，其中桨毂力的控制能力变化不大，F4x与F4y的控制幅度均为40%左右，F4z的控制幅度保持在85%左右；桨毂力矩的控制能力变化明显，初始状态下M4x，M4y的控制幅度在90%以上，当前进比提高到0.25后，其控制幅度不到80%。M4z的控制幅度由初始状态的80%变为60%。在工况改变的第15、30、45控制步，振动载荷各分量虽有波动，但总体上保持较低水平，只有垂向载荷F4z略微超过基准量。

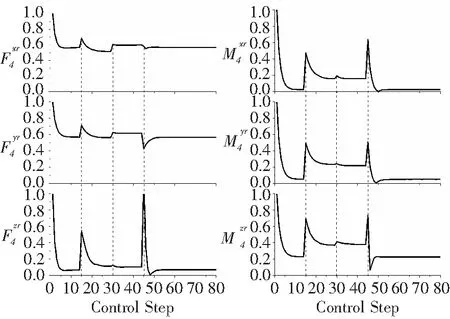
图12 4Ω旋翼桨毂载荷相对量

3 结论

本文针对ACF智能旋翼，构建了一种带传递矩阵在线识别的振动载荷高阶谐波控制方法，通过闭环控制仿真对该方法的识别精度、控制效果、参数影响以及鲁棒性等关键指标进行了分析凝练，形成结论如下：

1)对于周期性明显的稳态飞行，采用频域高阶谐波控制能有效降低旋翼桨毂主通过频率(NΩ)的振动载荷；

2)传递矩阵识别与控制量更新过程中涉及到大量矩阵求逆运算，为保持精度与数值稳定性，采用恰当的归一化或无量纲处理是必要的；

3)ACF智能旋翼振动载荷控制的关键是在襟翼驱动能力范围内实现载荷最小化，需要通过合理配置控制目标的权重矩阵来实现；

4)当闭环控制进程中旋翼工况发生变化，有可能导致某些方向的振动载荷产生较大的波动，而频域控制需要一定的时间才能产生控制效果，因此在试验过程中须对相关载荷进行实时监测，避免振动超限产生结构破坏。