高架覆盖采风口型街谷内PM2.5分布模拟

翟静 赵敬德 冯寒立

东华大学环境科学与工程学院

0 引言

随着城市化进程的加快，霾现象的发生频率，持续时间及影响区域都明显增加，城区中可吸入颗粒物的主要来源为汽车尾气[1-2]。而越来越多高架覆盖的街道峡谷的出现，影响着城市居民区的空气质量，危害沿街居民的健康。

街道峡谷这个概念从提出发展到现如今，已经有所扩展[3-4]，最典型的即为有高架路的街道峡谷。如今非典型街道峡谷为街道两侧建筑物中间存在开口、交叉口、采风口等，由此产生了并列式与错列式[5]。现有的研究中，实地测量[6-7]主要是对选定的特定街道空间区域的环境参数进行观测记录，分析比较数据，得到相关的规律。缩尺模型试验根据相似原理，采用风洞或者水槽进行相似实验[8]。近年来数值模拟方法逐渐成为主要研究手段[9-10]。

目前已有的研究主要集中于典型街谷，研究内容集中于污染气体[11-13]，存在采风口型非典型街谷以及街谷内可吸入颗粒物的研究较少，所用的衡量街谷内空气质量的评价标准只是针对整个街谷区域，而非人员活动区域。因此本文选取有30 m采风口的街谷进行了三维数值模拟研究，分析高架道路以及采风口的存在对街谷内颗粒污染物的分布影响，并以呼吸面高度的可吸入颗粒物平均浓度作为新的评价标准，对于改善街道峡谷微气候环境有实际参考意义。

1 模型与计算域

1.1 街道峡谷模型

如图1为高架覆盖下的街道峡谷计算域三维简化模型，假设所有的街道峡谷两侧建筑外形几何尺寸一致，根据实际街谷几何特征，模拟所取建筑长（L）=200 m，高（H）=18 m。经过模型简化，将建筑简化为面，计算域仅取街道峡谷所在空间，图中街道宽度W=40 m，高架路宽度B=14 m，高架路长度选取同建筑长度一致的200 m，高架路厚度（T）=0.5 m，高架路中心所在高度（H1）=12 m，此种情况下，街谷宽高比为2.2。本计算模型中（图1），A为采风口位置，采风口两侧建筑壁面为背风侧壁面，坐标原点取在背风侧壁面，B为双侧存在采风口时迎风侧壁面上采风口位置，两侧为迎风侧建筑壁面。街道峡谷背景来流风考虑街谷内颗粒污染物扩散最不利情况下的垂直于街谷轴线所在方向[14]，采用离散相模型（DPM模型）进行数值模拟。

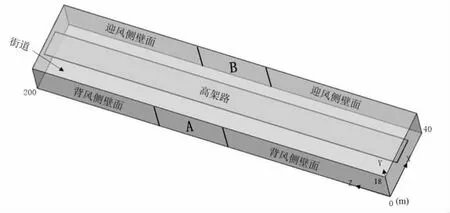
图1 街道峡谷物理模型

1.2 边界条件

街道中两条线源设置于模型坐标中的X=10 m和X=30 m处的位置，长度同街道长度为200 m。由于固态颗粒物源强难以估算，本文计算时依照市区早晚高峰时段进行选定，取 2 μg/s[15]，颗粒粒径取 2.5 μm。假定计算模型采风口所在计算域流速均匀，边界条件设为风速入口（velocity inlet），风速随高度拟合曲线[16]为Uy=y0.2375，单位为m/s，y为距地高度，单位为m。计算域上边界设为自由出流（outflow）[17]。壁面均为无滑移壁面，两侧边界设为对称边界（symmetry）。入口风速廓线设置于入口边界条件中，建筑顶端参考风速计算得V0=1.9 m/s，计算得其流动雷诺数为2×106，此计算结果大于雷诺数独立性所给出的参考标准，可以进行准确的数值模拟计算。

2 模拟结果

2.1 高架路覆盖下单侧存在采风口型街谷模拟结果

图2所示为高架路覆盖下单侧存在30 m采风口DPM模型下的颗粒物分布，在采风口通道内部的颗粒物浓度低。迎风侧区域颗粒物浓度低于背风侧，且背风侧越靠近采风口轴面的区域，颗粒物浓度越高，反之越低。这主要是受街谷内流场分布特征的影响。由图3的流场分布可以看出，采风口通道内部流场均匀。在采风口两侧分别形成两个大涡流，且次级涡流在近壁面和街口处。由此可以看出，颗粒物的分布情况与迎风侧流线分布密集、速度大、背风侧稀疏速度小，且次级涡流较靠近背风侧的流场分布特征相吻合。

图2 高架路覆盖下单侧存在30 m采风口DPM模型下的颗粒物分布

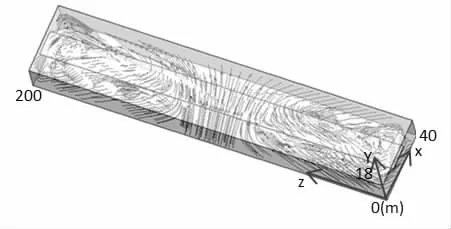
图3 单侧存在3 0m采风口的街道峡谷流场分布

对于有高架路覆盖单侧30 m采风口型街谷，在Y=1.5 m高度（呼吸面）的水平面上颗粒物分布表现出较明显的规律性，如图4。沿着X轴正向，主要表现出两种特征：一种是，当Z=20 m、60 m、80 m时，在X=0～20 m的区域内，颗粒物浓度先降后升，当X>20 m时，浓度表现为下降趋势。此现象的原因是流场分布表现为明显的涡流特征，由涡流的边缘至中心，产生第一次浓度下降的现象，上升的原因是高架路的存在会促进小涡流的生成，滞留污染物的运动。另一种是，当Z=0 m、40 m时，沿着X轴正向，污染物浓度逐渐下降，且整体浓度低于其他三个区域。这是由于此区域受次级涡流中心区域室外影响较小。同时，呼吸面高度颗粒物浓度分布还表现出一个比较明显的特征，迎风侧区域颗粒物浓度分布较背风侧相对均匀。

图4 单侧存在30 m采风口的街道峡谷Y=1.5 m高度的颗粒物分布曲线

2.2 高架路覆盖下双侧存在30 m采风口型街谷模拟结果

双侧存在3 0m采风口街谷颗粒物分布如图5所示。颗粒物分布出现明显的不均匀现象。街道峡谷两侧颗粒物分布呈现较明显的密集区与稀疏区：高架路区域分布较密集，靠近建筑物的两侧分布较稀疏。主要原因在于流场的影响。如图6所示，在采风口中心轴面（Z=100 m）两侧同样各自形成两个大涡流，且涡流的中心位于街道峡谷中心轴面（X=20 m）上。靠近端部的涡流较近采风口中心轴面的涡流表现出更明显的旋流特征。在旋流气流的带动下，颗粒物集中分布于涡流区域。

图5 双侧存在30 m采风口的街道峡谷DPM模型下的颗粒物分布

如图7所示，双侧模型内呼吸面高度上颗粒物浓度分布表现较明显波动性。总体趋势是：X<20 m时，颗粒物浓度有上升的趋势，X>20 m时，颗粒物浓度下降且下降幅度较快。在Z=20～180 m的中部范围内，颗粒物浓度变化相对较小，而端部区域，颗粒物浓度明显减小。

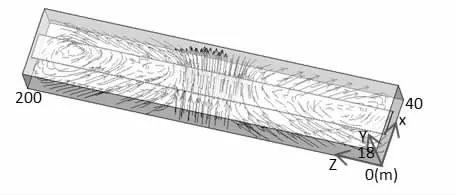
图6 双侧存在30 m采风口的街道峡谷流场分布

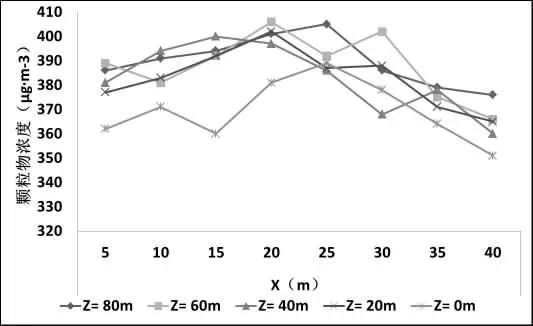
图7 双侧存在30 m采风口的街道峡谷Y=1.5 m高度的颗粒物分布曲线

2.3 有无高架覆盖模型的对比分析

现选取无高架路单双侧存在30 m宽采风口模型进行对比分析，以探究高架路对颗粒物分布扩散的影响。无高架路覆盖单双侧存在30 m宽采风口模型呼吸面高度颗粒物浓度分布曲线图如图8所示。

图8 无高架路覆盖30 m采风口型街谷模拟结果

由图8（a）可以看出无高架路模型呼吸面高度颗粒物沿X轴正向呈先降后升的趋势，主要因为无高架路覆盖时，高架路周围的小涡流影响消失，在较规则的大涡流影响下，中心区域速度低压力大，颗粒物在流场中受压力影响向涡流边缘区域运动。如图8（b）所示，呼吸面高度颗粒物浓度呈明显上升趋势，街谷端部区域浓度低于其余区域。

3 高架路的存在对颗粒物浓度分布的影响

为探究高架路的存在对颗粒物分布的影响，通过对高架路存在与否街谷内颗粒物浓度变化率的计算来进行量化。

表1为四种模型呼吸面高度可吸入颗粒物平均浓度值，由表中数据计算有无高架路模型可吸入颗粒物浓度值的变化量并计算其与无高架路时呼吸面颗粒物平均浓度值的比值。结果见表2，其中Cg表示颗粒物浓度变化率，颗粒物浓度的变化量用ΔC表示，无高架路时呼吸面颗粒物平均浓度表示为Cg0，μg/m3。

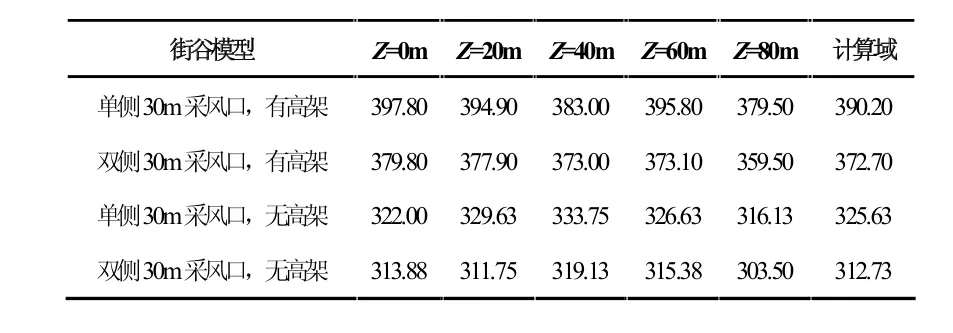
表1 不同采风口模型及高架路有无影响下的颗粒物浓度（μg/m3）

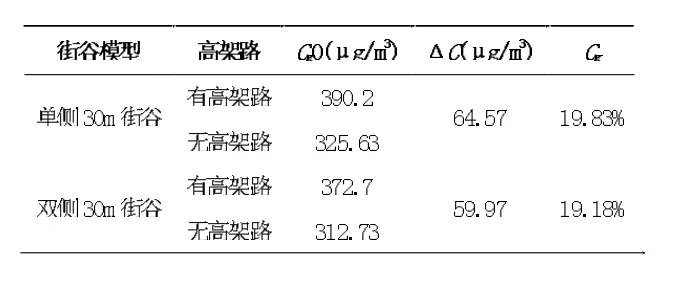
表2 不同采风口模型及高架路有无影响下的颗粒物浓度变化率

根据表2可得，单侧30 m采风口型街谷在有高架路影响下，计算域内颗粒物浓度的变化量ΔC=64.57 μg/m3，由于高架路存在的影响，颗粒物浓度变化率Cg=19.83%。双侧30 m采风口型街谷有高架路影响下，颗粒物浓度的变化量ΔC=59.97 μg/m3，由于高架路存在的影响，颗粒物浓度变化率Cg=19.18%。

模型内发散源强度持续不变，且线源布置位置按车流量不变情况设置。在现实街谷中，此模型及边界条件为上海市区早晚高峰时段，车流量较大且基本保持不变情况下，颗粒物的浓度分布。在建筑单/双侧存在30 m路口或采风口的街区情况下，高架路的存在会增大颗粒物的浓度，阻碍颗粒物向街谷外部扩散，增加率为20%左右。

4 结论

本文通过对有无高架路覆盖采风口型街谷进行三维CFD数值模拟，对两种模型进行了对比分析，并以呼吸面浓度作为评价标准，得到如下结论：

1）高架路覆盖单侧存在30 m采风口型街谷中，呼吸面高度迎风侧区域颗粒物浓度低于背风侧。背风侧越靠近采风口处的区域，浓度越高，反之浓度越低。

2）高架路覆盖双侧存在30 m采风口型街谷中，呼吸面高度可吸入颗粒物集中分布于高架路覆盖下的区域，两侧辅道及人行道区域颗粒物浓度较低。

3）在30 m宽采风口模型中，高架路的存在会增大颗粒物的浓度，阻碍颗粒物向街谷外部扩散，颗粒物浓度比无高架路模型增加20%左右。