基于ε–NTU理论的蒸气压缩式热泵循环模型研究

闵锐 喻李葵 刘韬 马卫武 刘刚

中南大学能源科学与工程学院

蒸气压缩式热泵系统作为一种高效节能的制冷、制热装置，在当今多元化的制冷、空气调节系统乃至热泵系统中仍备受青睐[1-2]。学者对蒸气压缩式热泵传热模型的研究，均以动态模型[3-4]与稳态模型[5]作为基本理论模型。而蒸气压缩式热泵系统在实际中常用于时间跨度较大的能源系统，例如分布式能源系统[6]、地源热泵系统[7-8]。由于稳态模型忽略了蒸汽压缩制冷系统及热泵系统中的所有不稳定的过程，当整个系统的瞬变时间常数远大于蒸汽压缩制冷机或热泵的时间常数时，稳态模型的模拟结果足够准确[9]。鉴于稳态模型具有简洁、便于计算等优点，本文将以此为系统建模的导向。

在蒸气压缩式热泵系统中，丁国良等[10]致力于建立简洁、普适性强、精确的传统模型，模型通过查阅工质在不同状态点的焓湿表或者焓湿图以获得对应焓值，从而通过数学计算求解。德国学者Alefeld[11]从热力学第二定律出发，建立一套仅涉及系统运行主要关键参数（蒸发温度、冷凝温度、蒸发潜热等）的系统性能系数解析模型。Klein等[12]建立了蒸汽压缩式制冷系统各主要部件的稳态集中参数模型，并就模型对设计出的制冷系统进行整体性能的分析和估算。梁彩华等[13]则应用“移动边界”方法对系统的换热器进行建模分析。为得到适用于工程应用的解析模型，本文作者基于熵分析方法，结合Alefeld提出的解析模型以及换热器的经典理论（ε-NTU理论）[14-15]对蒸气压缩式热泵系统进行建模仿真。

1 蒸气压缩式热泵模型建立

1.1 循环COP解析建模

为了简化蒸气压缩式热泵循环过程，提出以下假设：1）循环采用可逆绝热的压缩过程，即压缩机的等熵压缩系数为100%。2）制冷剂在循环过程中不存在过冷、过热现象，即进入压缩机的制冷剂为处于蒸发压力下的饱和干蒸气，进入膨胀阀的制冷剂液体为冷凝压力下的饱和液体。基于以上两个假设可得到该循环的压-焓图，如图1所示。

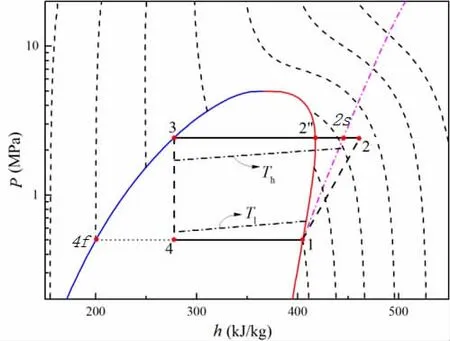
图1 简单理想循环p-h图

本文在德国学者Alefeld的简化研究基础上，通过进一步将模型中关键参数转化成循环状态点的温度值，从而达到系统的性能系数（COP）更加有利于计算机编程计算的目的。所得的COP解析式如下：

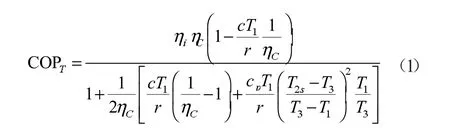
式中：T1，T3，T2s分别为蒸发温度，冷凝温度，压缩机等熵压缩出口温度；ηc为卡诺循环效率；ηi为压缩机效率；r为工质的汽化潜热；cp为工质的定压比热。

在COP解析式变量中，T2s为运行工质在过热状态下的温度参数，它获取不仅要借助实际气体状态方程，更要查阅精确的工质温熵图，对于模型的计算求解带来诸多不便。因此，将T2s用工质的热物性参数取代即可完成循环效率模型的构建。经查阅文献[16]，温度T2s与热膨胀系数可以通过克拉贝隆方程完成相互转换。在蒸气压缩式热泵循环中，对于压力小于10 MPa的过热蒸气，可视其为理想气体从而使用克拉贝隆方程。根据理想气体的状态方程，将热膨胀系数β用蒸发温度进行替代，最终温度T2s的替代结果是：

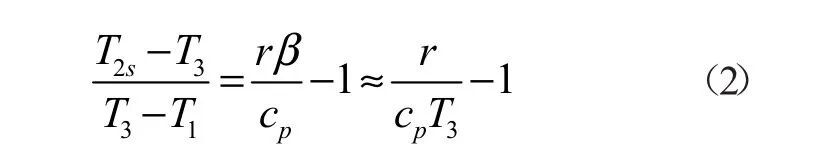
联立式（1）与（2），完成了蒸气压缩式热泵循环的制冷性能系数模型的建立，解析表达式如下：

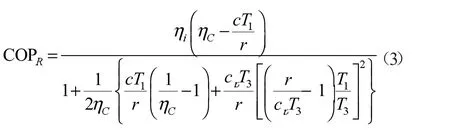
对于蒸气压缩式热泵循环，其热力学循环效率均是通过工质的温熵图或状态方程，结合焓平衡方程计算而得。该计算方法需要大量的计算资源和密集的编程工作。而本文推导出的解析模型极大地简化了计算，为工程实际中快速计算模拟蒸气压缩式热泵循环的热效率提供了有力的工具。

1.2 基于ε-NTU理论的耦合建模

1.2.1 制冷机组与用户侧的耦合模型

蒸气压缩式热泵系统中，通过蒸发器，冷凝器与冷却塔的能量传递，建立用户单元，制冷机组单元以及冷却塔单元之间的联系。依据换热器理论，将ε-NTU理论分别应用于上述热交换设备中，可联立构成一套算法简便的解析传热计算模型。实现制冷机组及冷却塔系统耦合建模的关键参数如图2所示：

图2 制冷机组及冷却塔系统能量传递图

对于系统中发生相变的蒸发器及冷凝器，基于ε-NTU理论的换热方程组如下：

式中：Q表示换热量；（cpm）表示换热介质的热容量流率；NTU表示换热器的传热单元数；ΔT表示换热介质的进、出口温度；ε表示换热器有效度。

在对蒸发器及冷凝器运用有效度时，做出以下两点近似：1）蒸发过程中发生相变，工质的定压比热可视为无限大。2）对于等熵工质与过热回降不明显的工质，近似等效冷凝过程温度不变（恒为T3）。因此，蒸发器有效度εe与冷凝器有效度εc可分别表达为：

根据制冷系数与热泵系数之间的关系，结合本文建立蒸气压缩式热泵循环的制冷性能系数模型与换热理论，制冷机组与用户侧的耦合模型即为：

式中：Th,in为冷却水的进口温度。

至此，通过制冷量Qe以及用户侧水流量参数的确定，即可求解出模型中其余全部变量。因此，制冷机组与用户侧的耦合模型建立完毕。

1.2.2 制冷机组与冷却塔的耦合模型

大量研究中冷却塔均被视为换热器进行模型计算，因此将ε-NTU理论应用于冷却塔中，且将逆流式冷却塔等效为湿空气与水的逆流换热器进行建模。通过假定塔内空气流的加湿过程等效为处于均匀温度下湿表面的空气流加湿过程，结合根据热质交换原理，得到冷却塔模型参数：

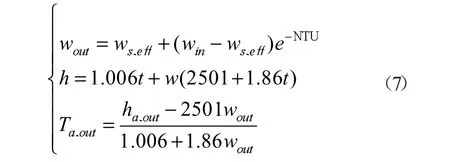
式中：ws,eff为 hs,eff所对应的饱和含湿量；win、wout分别为进出口空气的含湿量；w为湿空气含湿量；t为空气温度；Ta,out为冷却塔出口处空气温度；ha,out为冷却塔出口空气的焓值；wout为进出口空气的含湿量。

对于广泛使用的水-水相变式制冷空调系统，鉴于系统中所有换热器的传热单元数NTU以及系统运行制冷剂的热物理参数均可通过软件或手册确定，通过系统在可研性分析时对系统运行温度以及制冷量的评估，当系统在可研时加以确定运行工况，所建立的耦合模型均能对其余未知参数逐一求解。因而，完成了蒸气压缩式制冷机组与冷却塔系统的耦合模型。

2 模型运行分析与讨论

2.1 解析模型的验证

采用不同制冷剂在设定工况下进行仿真实验，通过传统算法与COPT的误差比对分析，从而确定解析模型的准确性。参考常规空调运行工况，蒸发温度均不超过10℃，冷凝温度一般低于40℃[17]。现取4种常见制冷剂，针对日常运行中由于用户侧需求的多样性而导致选取的蒸发温度不同，设定恒定冷凝温度变蒸发温度工况（即工况a）。具体工况参数在表1中列出：

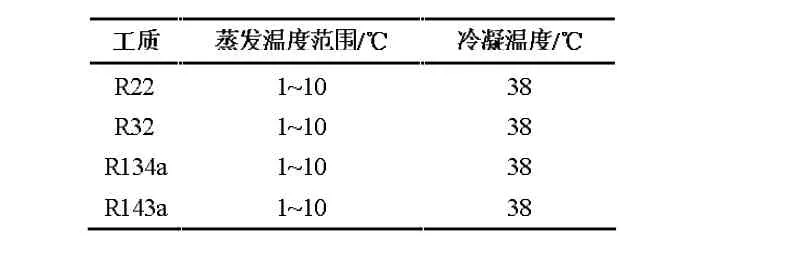
表1 四种常见制冷剂的变蒸发温度设计工况

两种模型在设计工况下的计算结果如图3所示：

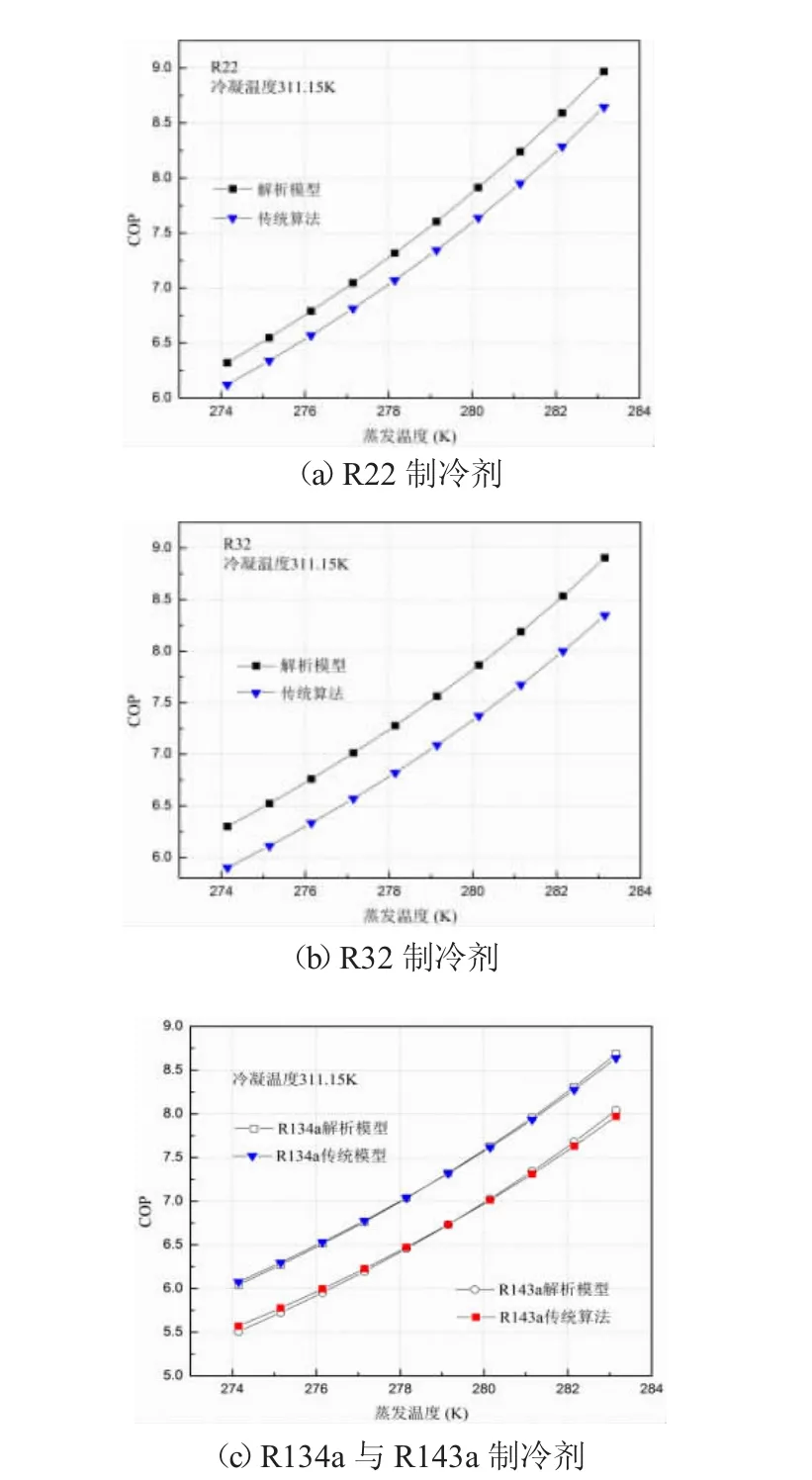
图3 变蒸发温度传统算法与解析模型计算结果对比图

图3以传统算法计算值为参照对象，在工况a下，4种制冷剂在两种模型中的最大相对误差由大到小依次为：R32对应的最大相对误差为6.76%，R22对应的最大相对误差为3.75%，R143a对应的最大相对误差为1.13%，R134a对应的最大相对误差为0.52%。除R32以外，其余三种工质的模型误差均小于4%，精度上足以证明解析模型正确与可靠。另外，两种模型对于该工况下R134a制冷剂而言，可视为等效模型。

压缩式冷热水机组运行过程中，冷凝温度同样会发生一定范围内的波动。因而对恒定蒸发温度变冷凝温度工况（即工况b）的实验也尤为重要。工况b参数详见表2：

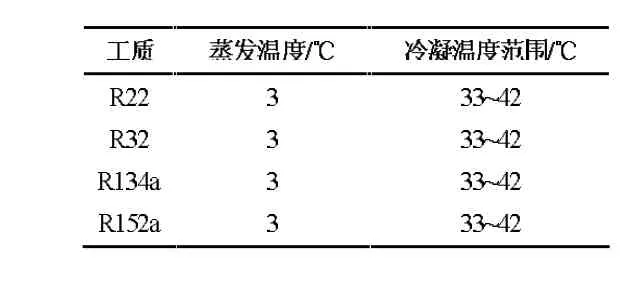
表2 四种常见制冷剂的变冷凝温度设计工况

图4 变冷凝温度传统算法与解析模型计算结果对比图

从图4中，可以看出：R32对应的最大相对误差为6.46%，制冷剂R22对应的最大相对误差为3.39%，R134a对应的最大相对误差为3.32%，R152a对应的最大相对误差为1.40%。解析模型的误差与工况a情况大致相同。但在工况b下，R134a在309～310 K之间，误差出现了陡增现象，这点在工况a中完全不存在。通过研究发现，制冷剂工质R134a处于循环的过热回降阶段（2s-2”）时，其平均定压比热cp的值在310 K时，由 10 J/(kg·K)的增速突变为 363 J/(kg·K)。因此，此现象通过公式（3）得以诠释。

经过两个工况的模型对比，并结合对比卡诺效率后，模型计算结果均小于对应温度下的卡诺效率，完成了对COP解析模型的验证。为了更准确的应用解析模型，对模型中冷凝温度取值范围以及制冷剂物性参数选取方面的考量不可或缺。

2.2 工况变化对制冷机组性能的影响

2.2.1 工况变化对制冷机组性能的影响

图5～7所示分别为制冷量，冷冻水流量和冷却水流量的变化对于压缩式制冷机组性能的影响结果。结合图5～7可为提高制冷机组性能提供方向。

制冷量作为压缩式制冷机组的重要输出变量，因会气候变化、人员多少等因素而波动不断。通过采用R22为运行工质，实验模拟压缩式制冷机组的性能随制冷量的变化趋势，数据结果归纳于图5。结果表明：当制冷量逐渐增加时，系统的制冷性能系数显著降低。当系统其他参数不变时，蒸发温度的降低或冷凝温度的提高是两个增大制冷量的因素，且蒸发温度的下降以及冷凝温度的升高，共同增加了系统的不可逆温差，从而导致了制冷性能系数的下降，冷凝温度与蒸发温度则升高、降低的范围均小于5℃。

图5 制冷量变化对压缩式制冷机组性能的影响

图6为恒定机组制冷量为240 kW时，冷冻水热容量流率对制冷机组性能的影响。从图中可知：冷冻水热容量流率的增加，致使系统的制冷系数升高，蒸发温度升高而冷凝温度下降趋势并不明显。当系统的制冷量确定且维持其余参数恒定时，随着冷冻水热容量流率的增加，蒸发温度势必升高。根据制冷效率的定义式，T3-T1的减小保证了COPR的增大。

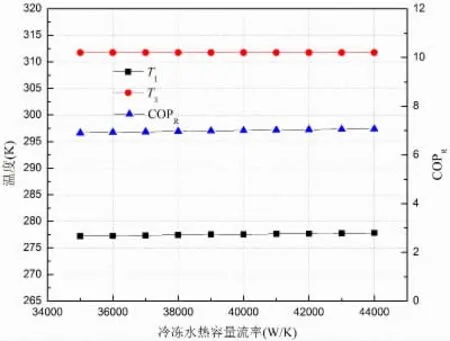
图6 冷冻水流量变化对压缩式制冷机组性能的影响

冷却水系统与压缩式制冷机组仅在冷凝器中产生热量交换，因此，蒸发温度的变化对于冷却水热容量流率无直接关系，即蒸发温度不随冷却水流量变化而改变。冷却水热容量流率的增加势必会改变冷凝器侧的换热量Qc，冷凝温度，COPR与冷却水热容量流率的变化关系如图7所示。

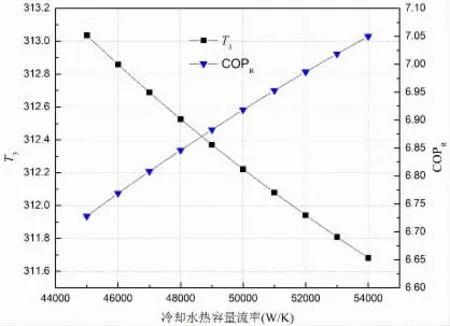
图7 冷却水流量变化对压缩式制冷机组性能的影响

2.2.2 工况变化对冷却塔性能的影响

图8～10是以冷却塔出口的温水是定值（即冷却水进水温度）为前提，通过制冷量、冷冻水流量和冷却水流量的变化，对空气冷却形逆流式冷却塔进行性能分析。

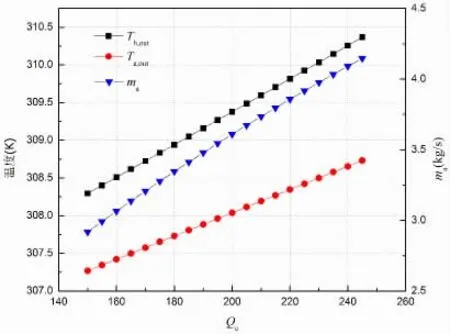
图8 制冷量变化对冷却塔性能的影响

从图8中看出：随着制冷量的增加，冷却塔进水温度，出口空气干球温度以及空气质量流量均呈现上升趋势。因为冷却塔换热量Qc增加，而冷却塔进口空气温度依旧为环境温度，则塔体出口空气的温度势必升高，而进出口处空气焓差的降低是导致空气质量流量增加的直接因素。

图9与图10分别为冷冻水热容量流率和冷却水热容量流率的变化对冷却塔侧性能的影响。实验结果显示：当冷冻水热容量流率增加时，冷却塔进水温度Th,out下降趋势缓慢，塔体出口空气干球温度降低、空气质量流量的减小同样不够显著。冷却水热容量流率的增加，会使冷却塔进水温度Th,out以及塔体出口空气干球温度Ta,out明显下降，空气质量流量显著上升。综上，对于实际工程运行中，先应当根据需求严格把控冷却水流量。采用加大冷冻水流量的方法，可使系统维持在额定工况运行条件下，有效地提高系统的效率。

图9 冷冻水流量变化对冷却塔性能的影响

图10 冷却水流量变化对冷却塔性能的影响

3 结论

本文基于ε-NTU理论建立仅以蒸发温度和冷凝温度为主要参数的蒸气压缩式热泵循环模型，不仅经过验证完全满足精度要求，而且非常适合对实际工程的应用。并通过 R22，R32，R134a，R143a 与 R152a 等五种工质进行的模型仿真试验，结果显示：

1）制冷剂R22的COP值较高且性能表现稳定，与传统算法相比，模型相对误差在3.04%～3.75%之间。

2）系统采用R22作为运行制冷剂时，仿真结果表明：冷冻水流量变化对压缩式制冷机组的性能影响和冷却塔性能影响不明显，而冷却水流量变化对压缩式制冷机组的性能影响和冷却塔性能影响较大。