一种基于KMP算法思想的字符串匹配算法的研究与实现

◆邵 岚 唐永群 孔令顺



一种基于KMP算法思想的字符串匹配算法的研究与实现

◆邵 岚 唐永群 孔令顺

（（CLO 北京 100054）

KMP算法是一种高效的字符匹配算法，它的思想在于其在匹配失败以后，不需要再对内容字符序列从头匹配，这样就减少了匹配的次数，提高效率。本方通过举例比较说明这个算法的优点。

KMP；模式匹配；KMP算法

0 引言

我们身处一个信息爆炸时代，每天产生的信息几乎都是海量。无论是金融、文学、生物还是计算机领域，文本都是必不可少的信息载体。而大到大型网站论坛，小到公司内部项目都不可避免的要涉及信息的查找、过滤等相关功能，比如在一个文件中查找出所有给的字符串，然后过滤，不好的设计思想导致迟迟得不到结果，无法满足实时性高的要求，这个过程中如何高效的处理就显得尤为重要，各种字符串查找匹配算应运而生。

基于目前公司项目开发中正好要用到字符串查找功能，借此机会对字符串匹配算法做一次分析与比较，希望能对项目的运行效率有所裨益。

本文先简单了解BF算法，随后介绍KMP算法及其思想、move数组的求解，最后介绍KMP算法在项目中的实现和简单应用。

1 BF算法

BF算法的基本思想比较简单，就说从内容串C的第一个字符开始和关键字串K的第一个字符开始逐个进行比较，如果相等则进一步比较二者的第二个字符，依次往后移动两者的指向，如果在某个字符比较时失配了，则分别将关键字串K的第一个字符与内容串的第二个字符作为最初指向再重新进行比较，匹配时指向各自向后移动一个位置，以此类推。

下面通过一个简单的例子，我们可以来了解一下BF算法的原理。假设有一个内容串C和关键字串K，C=”xyxyy”，K=“xyy”,也就是在C中去匹配K。由于例子比较简单，我们可以绘制出整个的匹配过程。如图1所示。

BF算法的基本思想从图中的七个过程就能得到完整的体现，简单的描述一下上面的流程是这样的：首先以关键字串K的第一个字符和内容串C的第一个字符作为各自的起始位置进行比较，经过前两次的匹配都成功后，这时的比较位置都移动到第3个字符，也就是将关键字串的第三个字符’y’与内容串的第三个字符’x’比较，由于不能匹配，就要进行下一轮的重新匹配，也就是要重新确定比较的初始位置。对于模式来说，重新定位就是第一个字符作为初始比较位置，而对于内容串来说就是移动一个位置而不是上一次匹配成功的最后位置。BF算法的实现比较简单，思维方式也很直接，但是存在不足之处：就上面的例子来说，内容串的定位”走了回头路”；而且比较操作也重复执行了：第一次失配后，在接下来的第二次匹配时，我们会首先用关键字串的第一个字符与内容串的第二个字符比较，但是这个过程是可以省略的，因为我们通过观察关键字串可以发现关键字串的前两个字符是不相等的，而上一轮比较过程中，关键字串的第二个字符与内容串的第二个字符是想等的，因此可以判断关键字串的第一个字符与内容串的第二个字符是不相等的。如果能在比较过程中避免这些重复比较，匹配效率也将得到很大的提高，KMP算法则正好避免了上面BF算法的不足。

图1 匹配过程

2 KMP模式匹配算法

2.1 算法前瞻

KMP算法之所以高效，在于其在匹配失败以后，不需要再对目标字符序列从头匹配，这样就减少了匹配的次数，提高效率。算法实现的核心就是基于一个move数组，move数组存储了关键字串的特征信息。

下面图2我们举一个例子，从中体会一下KMP算法的思想并且与BF算法做一下比较，就能找出KMP算法的高效所在，假设有一个内容串C和关键字串K ，C=” ababcabcacb”，K =”abcac”，当比较到到第二个字符时出现失配，即C[2]！=K[2]。

图2 例子

这时如果按照传统的BF算法，则第二轮的比较应该从内容串的第一个字符与关键字串的第零个字符开始，这种思想前面我们已经知悉。KMP算法则会首先发现K串本身的一些特性，即最开始的两个字符是不相等，同时根据第一轮的比较发现：C[0] = K[0]，C[1] = K[1]。因此可以立即得出结论C[1] != K[0]，所以可以省略它们的比较，直接从C第二个字符与K第零个字符进行比较开始，如图3：

图3 第二轮比较

从图中可以看到，当比较到C[6]和K[4]时，再次出现失配情况。根据KMP思想只要从C[6]和K[1]开始进行比较即可。如图4：

图4 从C[6]和K[1]开始进行比较

可以看到整个过程中只发生了3次重新匹配，就得到了匹配成功的结论，加快了匹配的执行速度。上面的例子只是大概描述了方法的思路，但是这种方法的本质到底是什么，又如何才能精确的描述，最后到代码的实现，我们下面就来解决这些问题。

2.2 KMP模式匹配算法思想

通过上面的例子分析，我们可以看到整个匹配过程中，失败时只对关键字串K的初始比较位置回溯，而内容串的比较位置一直是向后，没有重复。

我们得到的结论是：KMP算法思想关键在于匹配失败时，我们能够知道从关键字串的哪一个位置与内容串在失配时的位置重新开始比较，定位关键字串的重新比较位置就是整个算法思想的关键，而这些都与内容串没有干系。

KMP算法的关键是它的move数组，利用move数组能够高效地确定在当前失配的情况下，应当将关键字串移动多少位才能够避免不必要的匹配。KMP如何借助move数组移位，道理其实很简单，如果内容串和关键字串的字符匹配，那么就同时移动两者的下标；如果不能匹配，关键字串就使用move数组来获得移动的数目。

2.3 求解move数组

move数组的含义：如果关键字串K与内容串C匹配到了n个字符，这n个字符也就是关键字串K的前n个字符，我们对这个子串记为tmp做如下分析：

这个串tmp的前后是否有重复的内容，哪怕是重复一个字符，当然越多越好，我们也只记录最多的重复情况，这个最多的长度就是下次重新匹配时不需要再次匹配测试的长度，同时也要记录这两个重复的部分之间的间隔距离，这个距离就是失配时关键字串K的回溯长度。为提高效率，匹配长度n就是move数组的下标。我举一个例子同时附一个表格来体会一下思想：

解析一下：

比如对于匹配到了2个字符，也就是K与C的前两个字符都是ab，也即是K[0]=C[0], K[1]=C[1],但是K[2]!=C[2]失配，继续比较时，将K的指针回溯到K的头部再偏移move[2]=0个长度，这也应该是K的最前部，而C不用回溯。

假设关键字串K = “abxabyz”,计算结果如表1：

表1 计算结果

比如对于匹配到了5个字符，也就是K与C的前两个字符都是abxab，也即是K[0]=C[0], K[1]=C[1]…K[4]=C[4]但是K[5]!=C[5]失配，继续比较时，将K的指针回溯到K的头部再偏移move[5]=2个长度，而C不用回溯，也就是用K中的K[2]=’x’字符与C[5]比较而不是K[0]与C[1]做比较。

2.4 求解move数组的算法实现

代码其实并不复杂，整体思路是对于每一个关键字串与内容串匹配到的长度j，得到匹配的内容tmp，然后将 tmp分拆为前后两个部分，称为前缀和后缀，在前缀长度不大于后缀长度下，判断前缀是否在后缀中重复出现。匹配长度作为move数组的下标，前缀在后缀中能够找到重复时的最大长度值存放在move[j]中。move数组的初始值都是0，意思是关键字串默认都回到头部并且没有偏移。

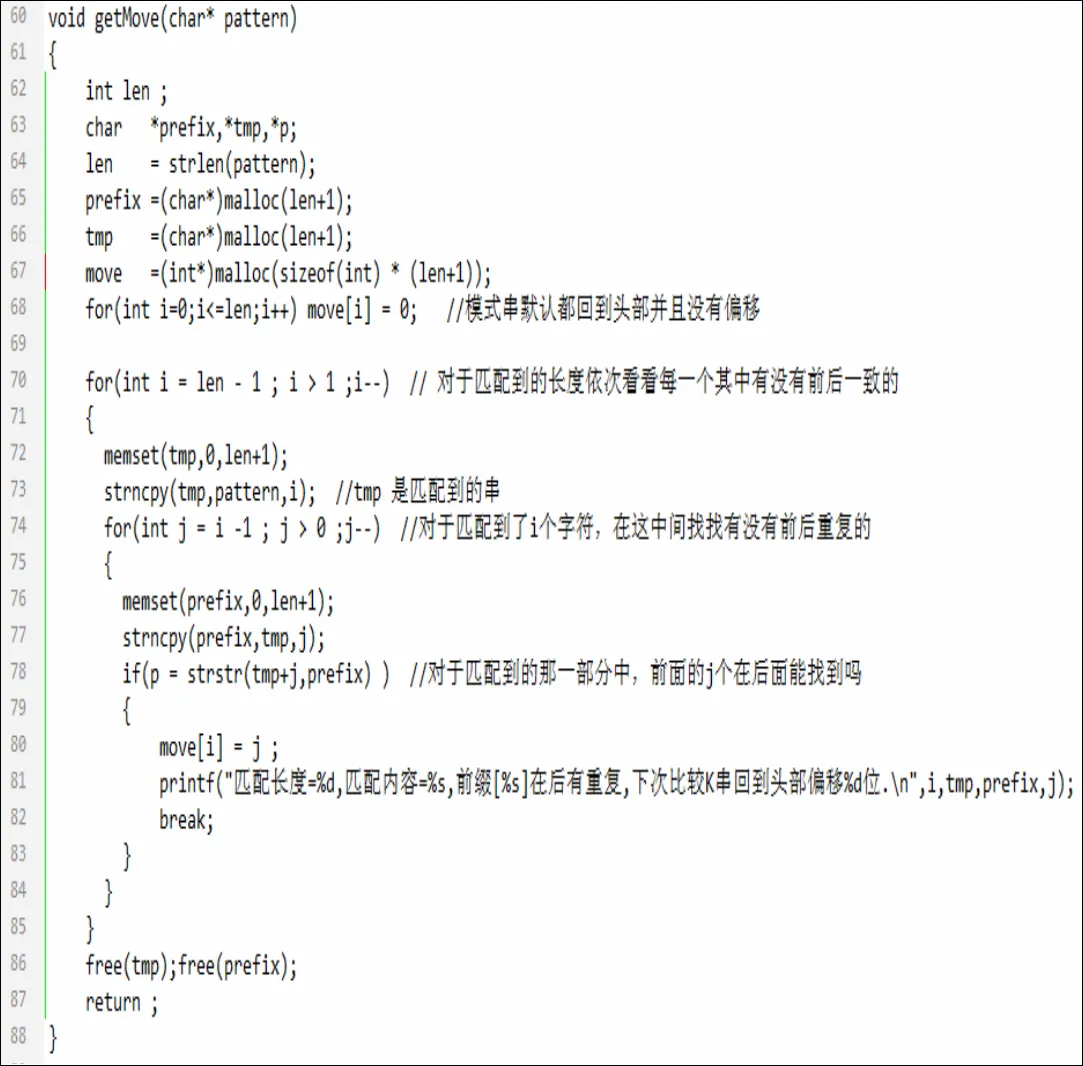
图5 求解move数组的算法实现

3 算法在项目中的实现与应用

3.1 KMP模式匹配算法实现

函数的功能是基于KMP思想，在内容串中找出所有的关键字串的位置。简单的解释一下：matchlen是匹配长度的计数器，每次字符比较成功就+1（37行），当完全匹配时（38行），matchlen置0（43行），重新开始计数。当出现失配情况时（50行），如果已经匹配的长度是0，也就是第一个字符就不匹配，就要后移内容串指针（52行）。move[matchlen] （53行）中的matchlen表示已经成功匹配了多少个字符，move[matchlen]则表示在成功匹配了matchlen个字符的情况下，前缀中有多少个字符在后缀中重复出现，所以下一次重新比较时，关键字串要定位到头部再偏移move[matchlen]个长度（54行）。跳过的长度move[matchlen]虽然是不用重复比较的长度，但是还是要算匹配长度的，所以有53行的赋值。

图6 KMP模式匹配算法实现

3.2 KMP算法应用

代码很简单（图7），看一下执行结果（图8）：

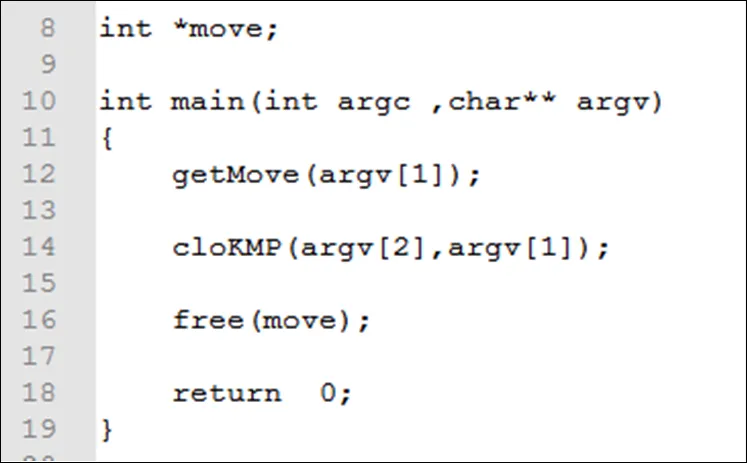
图7 代码

图8 执行结果

4 结束语

本文从BF算法讲起，随后阐述KMP的算法思想以及优势、move 数组的简单求解以及KMP算法在项目中的实现。通过分析BF算法和KMP算法并通过实验证明在字符集较大的情况下，KMP算法在运行比较次数和运行时间上都优于BF算法。综上所述，KMP算法提高了匹配效率，具有广阔的应用前景。

通过上述对算法的分析，以及对不同算法的实现的运行效率比较，为我们更清楚的分析算法的优劣，去选择对自己更实用的算法，提供了可遵循的方式方法，并广泛应用到自己的学习工作中。

[1] KMP算法详细讲解: https://blog.csdn.net/suguoliang/article/details/77460455

[2] KMP算法Move数组计算: https://blog.csdn.net/xiao xian8023/ article/details/8134292