ECC加密算法分析及应用研究

◆赵梦婷 李斌勇 李文皓 阎泽诚 高家奇 齐佳昕 廖怀凯



ECC加密算法分析及应用研究

◆赵梦婷 李斌勇 李文皓 阎泽诚 高家奇 齐佳昕 廖怀凯

（成都信息工程大学网络空间安全学院 四川 610225）

椭圆曲线加密算法是建立在基于椭圆曲线离散对数问题上的非对称密码体制，凭借其密钥短的优势得到了广泛应用。本文首先从数学角度分析了椭圆曲线加密算法的原理，然后对银行间通信数据加密原理展开了研究。在此基础上，结合ECC算法剖析了数据通信的步骤，并给出了相应的加密通信流程。最后结合USB key的制作及验证流程，研究了ECC算法在网银通信交互过程的加密应用。本文所开展的研究，为保障数据通信安全提供了一种可行的技术方案。

密钥；ECC；椭圆曲线；加密通信

0 引言

随着信息化以及数字化社会的发展，用户对信息安全和保密的重要性的认识不断地提高。由此，许多加密算法应运而生，如对称加密算法DES、非对称算法RSA、散列算法等。需要明确的是，数据安全是相对的，随着硬件、网络以及各方面的发展，目前常用的加密算法都可能在短时间内被破解，为此需要不断改进密钥或算法才能在接下来的一段时间中保证数据安全。

椭圆曲线加密算法（ECC）是基于椭圆曲线数学的一种非对称密码算法，是建立在基于椭圆曲线的离散对数问题上的密码体制。随着分解大整数方法的进步以及各方面的完善，RSA算法渐渐不能满足现状，ECC算法的需求性逐渐增大。ECC以其明显的“短密钥”优势得到了广泛应用，并逐渐被确定为许多编码方式的数字签名标准。诚然，ECC还有许多未解决的问题，不过这种引用了丰富数学理论的算法，也印证了将更多数学有较大可行性理论应用到密码学这一领域中。

1 加密算法分析

首先从数学角度阐释算法加密原理，其椭圆曲线方程如下：

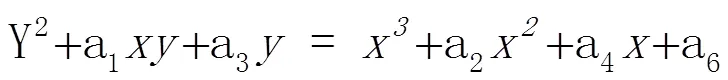
其中，系数ai定义在某个域上（密码算法中需要把之前连续曲线变为有限域上的点，故ai也定义在有限域中）。曲线上所有点和一个无穷远点构成一个集合连同定义上的加法（eg：a+b≡c (mod p)）构成阿贝尔群。由于曲线上每一点都是非奇异点，故可在椭圆曲线上找到两点P、Q，且存在如下关系式：

由此可见，已知m、P求Q较为容易，反之由Q逆向求m、P难度却较大，椭圆曲线密码正是基于该机制来展开设计及应用。

2 ECC加密通信应用

随着支付宝、微信等线上支付等方式的发展，越来越多的货币交易也向着网络化，信息化深度发展。因此保证网络上传递资金信息的安全性，用户信息数据的安全性也逐渐成为银行网络信息化建设的主要目标。

为此，尝试将ECC算法运用于其中，鉴于银行系统较为复杂，且不同的模块使用不同的加密方式。研究之后发现在银行间的信息通信加密可以通过ECC算法进行优化。

首先，研究银行间通信数据加密的原理

通过研究发现银行柜台间使用专线网络，被攻击的可能性较小。然而银行间的数据交互使用公共网络，此时可使用ECC算法进行数据加密。

如图1所示为银行加密示意图，通过采用ECC算法完成上述数据通信，具体步骤如下：

Step2：A端选择一条椭圆曲线Ep(a,b)，并取曲线上一点为基点G；

Step3：A端选择一个私有秘钥k，生成公钥K=kG（正如上述原理所说知道K求k较为困难）；

Step4：A端将曲线方程Ep(a,b)，K，G等信息传给B；

Step5：B端接收数据并计算 C1=M+rK（r为随机数），C2=rG；

Step6：B端返回C1、C2给A；

Step7：A端计算C1-kC2=M，计算表达式为：

其加密通信流程如图2所示。

图2 加密通信流程

通过上述论述不难发现影响到加密算法安全性的条件有：

(1)p需要其值越大越好，然而当p过大时会影响计算速率，一般200位左右就可以满足一般的安全需求；

(2)p≠n*h；

(3)pt≠（1modn），1≤t＜20；

(5)n为素数，因为分解成非素数相对容易，大整数做素数分解是比较难的，安全性更高；

(6)h≤4；

通过上述过程发现，若有攻击者H，此时攻击者只能得到Ep(a,b)，K，G，C1，C2，得到k、M是非常困难的。银行间通信由此完成加密，而相较于RSA算法加密，ECC具有抗攻击性强、CPU占用少，网络消耗低、加密速度快的优点。

3 网上银行加密应用

用户除了直接前往银行处理业务外，还可通过网上银行来进行业务处理，保证用户数据信息就是重中之重。目前大部分网银采用USB key作为证书，USB key是包含用户个人身份信息、公钥和数字签名的一个特殊的电子文件的一种数字证书。USB Key之所有是较为安全的系统，是因为产生公私密钥对的程序是研制者直接烧制在芯片中的，公钥密码算法程序也是烧制在芯片中。公私密钥产生后，公钥可以导出到USB Key外，而私钥则存储于密钥区，不允许外部访问。

现将ECC算法加入到USB key的制作中，应用ECC算法，通过其签名和认证模块的相对独立性和安全性往往可使数据得到更好的加密。相应的序列号制作及验证流程如图3所示。

图3 序列号制作及验证流程

针对用户加密，其算法步骤如下：

Step1:用户A选择一条椭圆曲线Ep1(a,b)，和基点G1；银行B选择一条椭圆曲线Ep2(a,b)，和基点G2；

Step2:A选择私有密钥k1（k1

Step3:A对数据M首先进行哈希加密，M=HASH(M)；

Step4:A、B随机产生r1，r2；

Step5:先用用户A私钥k1 对消息进行加密，消息M=r 1- M* k1 (mod n1)；

Step6:为防止数据不会传递到错误地方，再用银行B公钥K2对消息进行加密；M=r 2- M* K2 (mod n2)，随后将加密消息连同之前的哈希值传递给银行B；

银行解密算法步骤如下：

Step1:银行B收到消息后先用自己的私钥k2解密，M=M*G2+Hash*k2 (mod p2)；

Step2:银行B再利用用户A的公钥解密，M=M*G1+Hash*K1 (mod p1)；

Step3:将最后得到的哈希值与之前的哈希值信息比较，若相等则表明数据没有被中途篡改，可以继续通信。

4 结束语

本文主要研究了ECC算法的原理以及在银行系统中的简单应用。文中提出了将ECC加密算法应用于银行间数据通信，以及网上银行的加密过程中，为保证数据通信的安全提供了一种可行的技术方案。未来研究中，力求将进一步完善这一算法在应用中的具体实现。

[1]田文章. 网络系统安全中混合加密技术研究[D].南京邮电大学,2017.

[2]王全福. 基于ECC的同态加密算法研究与改进[D].中北大学,2017.

[3]黄荣梅.基于椭圆曲线加密算法的信息安全系统[J].内江师范学院学报,2017.

[4]王惠,朱骥.国密算法在网银系统中的应用实践[J].金融电子化,2015.

[5]张永建. RSA算法和SM2算法的研究[D].江西理工大学,2015.

[6]陈飞. ECC公钥加密算法的研究与实现[D].华中科技大学,2015.

国家自然科学青年基金项目(71701026)、四川省科技计划项目(2018GZ0307)、四川省教育厅重点项目(17ZA0069)、成都市科技局软科学项目(2016-RK00-00089-ZF)、成都信息工程大学科研基金资助项目(KYTZ201618)。