基于NSGA-II算法的混合动力汽车多目标优化

吕竞伦 凌和平 孟繁亮 田果 李桂忠 朱嘉鹏

（比亚迪汽车工业有限公司）

混合动力汽车的性能优化目标是在满足各个部件性能约束的前提下，降低系统成本，提高动力性、经济性及平顺性等。现阶段对混合动力汽车进行性能优化时，在计算方法上，通常采用枚举法，将决策变量排列组合计算。当决策变量数目较多时，组合计算的效率会大打折扣。在对优化问题的处理上，通常是将多目标问题设定权重简化为单目标问题，但未考虑各目标间的相互影响，难以反映优化目标的真实情况[1]。针对上述问题，文章以某并联式混合动力四驱车型为研究对象，将多目标遗传算法应用于动力性及经济性的多目标优化中，得出一组Pareto解集，在不受主观因素影响的情况下，进一步优化了整车性能。

1 研究对象及优化模型

1.1 研究对象

以某款插电并联式混合动力四驱车型为研究对象，将发动机各挡速比及前后电机速比作为决策变量，对100 km加速时间、油耗、电耗进行多目标优化。整车动力结构，如图1所示。动力系统主要包含1个发动机和1个驱动电机，用于前轴驱动；1个驱动电机，用于后轮驱动；动力电池经逆变器分别与2个驱动电机相连。前轴变速器采用DCT变速器，然后经前主减速器、差速器、半轴，将动力传输至前轮。

图1 插电式混合动力四驱汽车系统结构图

1.2 优化目标

典型的多目标问题由1组目标向量、1组等式约束向量、1组不等式约束向量以及n维决策向量组成，其数学模型表述为：

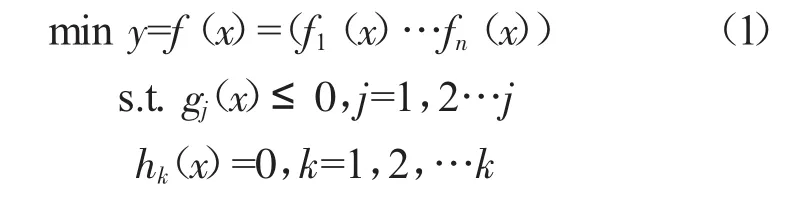
式中：x——决策变量；

f——n维目标向量；

gj——j维不等式约束向量；

hk——k维约束向量；

y——目标函数。

文章建立的优化目标是在提升动力性的同时，使某循环工况的油耗和电耗尽可能更低。由上述数学模型建立混合动力汽车多目标优化的数学模型，如式（2）所示。

式中：f1——油耗，L/100 km；

f2——电耗，kW·h/100 km；

f3——100 km加速时间，s。

其中，决策变量（x）在该优化问题中为发动机及前后电机的速比，可表示为：

式中：in——发动机n挡速比，n=1，2…6；

img1，img2——前、后电机速比。

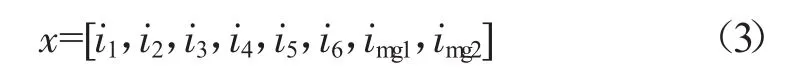
1.3 约束条件

混合动力汽车优化问题的约束条件主要是满足整车动力性能指标及变速箱的设计条件。结合当前车型动力结构，由此制定如下所示约束指标。

1.3.1 最高车速约束

最小传动比应满足最高车速时的发动机及前后电机的转速约束条件，并且输出扭矩应大于整车阻力矩。则约束条件可表达为：

式中：nmax_eng——发动机最高转速，r/min；

nmax_mg1，nmax_mg2——前、后电机最高转速，r/min；

r——轮胎半径，m；

vmax——最高车速，km/h；

Fvmax——最高车速下的整车阻力矩，N·m；

Tmax_eng——发动机峰值扭矩，N·m；

Tmax_mg1，Tmax_mg2——前、后电机峰值扭矩，N·m。

1.3.2 最大爬坡度约束

最大传动比应满足最大爬坡度要求，并且输出的驱动力应不大于地面最大附着力。则约束条件可表达为：

式中：m——整车质量，kg；

g——重力加速度，g=9.8 N/kg；

CD——风阻系数；

A——迎风面积，m2；

α——最大爬坡度，（°）；

vp——爬坡车速，km/h；

φ——路面附着系数；

f——滚动阻力系数。

1.3.3 换挡条件约束

相邻挡位之间传动比的比值不宜过大，否则会造成换挡困难，一般认为比值不宜大于1.8。而各挡位传动比应单调递减，因此比值应大于1。则约束条件可表达为：

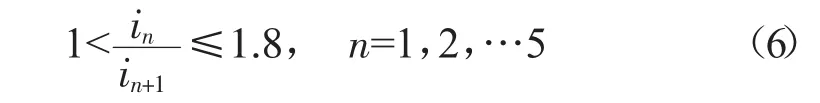
1.4 仿真模型

根据车辆动力学搭建整车Simulink仿真模型，便于后期算法的调用。模型包括：1）驾驶员模型；2）动力源模型：发动机模型、前后电机模型及电池模型等；3）传动系统模型：变速器模型、车身模型、差速器模型及轮胎模型等；4）控制模型：整车控制模型、ECM控制模型、TCU控制模型及BMS控制模型等。在此文章仅简述以下2个典型的仿真模型。

1.4.1 驾驶员模型

驾驶员模型中采用PID控制算法，以实现减小实际车速与目标跟随车速之间的偏差。将工况目标车速（vo/（km/h））和仿真模型输出的实际车速（v/（km/h））输入驾驶员模型，二者差值作为基于PID控制的速度反馈控制器的输入，输出为踏板行程。踏板行程限制范围为[-100,100]。踏板行程如果为正值，相应输出油门深度信号，而制动深度信号为0，反之则输出制动深度信号，油门深度信号为0。

控制算法，如式（7）所示。

式中：Kp，Ti，Td——比例、积分、微分系数；

t——采样时间，s；

e（t）——仿真工况中目标车速与实际车速的差值，km/h；

u——踏板行程，%。

1.4.2 发动机模型

发动机模型包括扭矩计算模块和油耗计算模块2个子模块。

扭矩计算模块通过ECM控制模型输出的发动机指示扭矩和发动机转速，计算发动机实际扭矩。

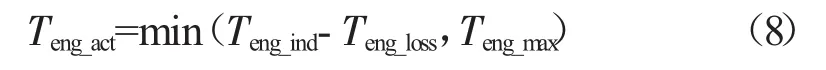
式中：Teng_act，Teng_loss，Teng_max——发动机实际、损失、峰值扭矩，N·m；

Teng_ind——ECM发送的发动机指示扭矩信号，N·m。

油耗计算模块根据稳态工况下的发动机万有特性标定数据，由发动机当前转速和实际扭矩实时计算瞬时燃油消耗率，再由式（9）即可得出整个工况的油耗。

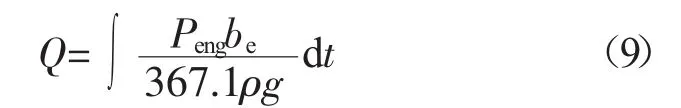
式中：Q——总油耗，L；

Peng——发动机功率，kW；

ρ——燃油体积质量，ρg一般取6.96～7.15 N/L[2]；

be——发动机燃油消耗率，g/（kW·h）。

2 NSGA-II优化方法

2.1 NSGA-II算法简介

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，通过模拟自然进化过程搜索最优解。在计算时只需要影响搜索方向的目标函数和相应的适应度函数，通过在决策变量可行域内进行多次迭代计算，大范围搜索寻找最优解。该算法不依赖于问题的具体领域，对问题的种类有很强的鲁棒性。

而第2代非劣解排序遗传算法（NSGA-II）是目前广泛应用的多目标遗传算法之一。该种算法采用快速非支配排序法和拥挤度算子选择个体，然后通过遗传算法交叉和变异，最终生成Pareto最优解集，算法运算流程，如图2所示。NSGA-II在解决复杂的多目标优化问题时，具有运算速度快、解集收敛性好的优点，其使计算复杂度降低，并保持了种群多样性。

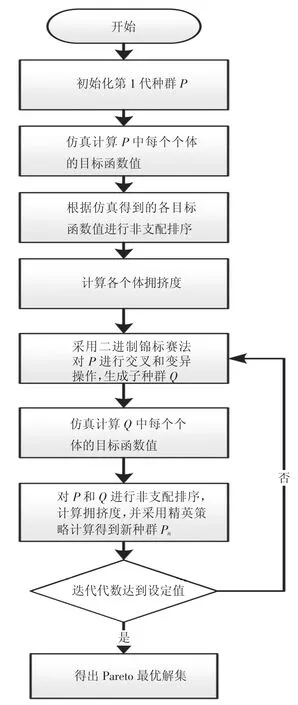
图2 非劣解排序遗传算法（NSGA-II）流程

2.2 Pareto最优解

在只有1个目标函数的情况下，优化函数的全局最优解与其他解的优劣，比较容易直观理解。解与解之间可通过直接进行数值比较得出大小来确定其为全局最优解。

而对于多目标问题，很难找到一个解使得所有的目标函数同时最优，特别是对于需优化的目标数量较多的情况。更多的结果是，某些解使得某个目标函数的值最优时，对于其他的目标函数而言，其值却不是最好的，甚至可能是最差的，这些解之间就全体目标函数而言是无法比较优劣的，特点是：无法改进任何目标函数的同时不削弱至少1个其他目标函数，这组解集就是Pareto最优解集。

2.3 算法运算流程

文章所建立的优化模型用MATLAB实现。其中NSGA-II遗传算法用MATLAB/M-File文件编写，计算目标函数时调用MATLAB/Simulink/Stateflow搭建的整车仿真模型。结合文章中以100 km加速时间、100 km油耗和电耗为优化目标，NSGA-II具体优化流程如下：

1）随机产生第1代种群P；

2）将P依次代入Simulink仿真模型中求解，得出100 km加速时间、100 km油耗和100 km电耗作为目标函数值（f）。考虑到约束条件，对目标函数加入惩罚因子。当决策变量x满足约束条件，∀j∈{1，2，…j}，均满足gj（x）≤0，则最终目标函数值F=f，否则，F为无穷大的值。

3）根据F值，进行快速非支配排序，确定每个个体的支配等级。这里的支配定义是：对于目标函数f（x），在决策变量x的可行域区间的2个个体p和q，∀i∈{1，2，…n}，均满足f（pi）≤f（qi），且∈i∈{1，2，…n}有f（pi）＜f（qi），则称p支配q[3]。快速非支配排序中，将P中不被其他任何个体所支配的个体划分为第1等级，只被第1等级支配的个体划分为第2等级，以此类推，直到种群中所有个体的等级都被确定。

4）计算个体拥挤度。拥挤度表示在种群中某个体的周围个体的密度，直观上用个体N周围包含N但不包含其余个体的最大长方形的长来表示，如图3所示。

图3 种群个体拥挤度

拥挤度的计算方法如下：在同一支配等级下，基于某单一目标函数对个体进行排序，最大和最小个体拥挤度为无穷大，其他个体N的拥挤度为：

式中：I（N），I（N+1），I（N-1）——第N个、第N+1个、第N-1个个体对应的单一目标函数值；

fmax，fmin——当前个体中最大的、最小的单一目标函数值。

5）采用二进制锦标赛法从种群P中选择一部分个体进行交叉和变异操作，产生新个体。交叉的原则是重复将个体两两对比，支配等级高、拥挤度大的个体参与交叉操作，直到交叉后的种群达到指定个数。变异的原则是在P中随机选择一部分个体，进行变异操作生成新个体。

6）将种群P和交叉、变异的个体合并，计算该种群的支配等级和拥挤度，按照支配等级越高、拥挤度越大，被选择的概率越大的原则，选择个体使子代种群与父代种群个数一致。

7）重复第5）和第6）步的操作，直到迭代次数达到设定值，最终种群的个体就是Pareto最优解集。

3 优化结果分析

文章在优化过程中，100 km加速计算以运动模式下全油门加速作为测试工况，经济性中的100 km油耗和100 km电耗计算以经济模式下，初始SOC=80%、目标SOC=25%运行一个WLTC工况作为测试工况，如图4所示，该工况比较能反映实际驾驶路况。

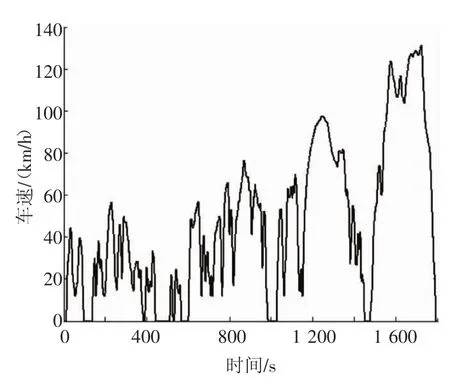
图4 某混合动力汽车WLTC工况时间-速度曲线

算法设定种群规模为100，最大迭代次数为50代，最终得到Pareto最优解集。图5示出某混合动力汽车Pareto最优解集分布图。图6示出最终的Pareto前沿。

图5 某混合动力汽车Pareto最优解集分布图

图6 某混合动力汽车最终的Pareto前沿

与优化前对比可以得出，各目标都得到一定程度的改善。得到的Pareto解集分布图为设计者提供了直观的多目标设计方法。在整车设计过程中，设计者只需结合设计需求，从图6中（Pareto前沿）选取相应的目标点作为设计目标，即可得到相应的优化参数。

从中挑选5组最优解集，列举如表1所示。第0组为车辆默认设置，第1～5组为优化后的最优Pareto解集。观察表1中数据可以发现，在保证整车基本性能的前提下，动力性和经济性能均得到提升。其中100 km加速时间最大缩短了10.79%，100 km油耗最大下降了14.82%，100 km电耗最大下降了8.39%。

表1 某混合动力汽车部分Pareto最优解集

4 结论

文章针对混合动力系统属于多目标优化的本质，以动力性与经济性为目标，建立了相应的多目标评价模型与多目标优化算法，在保证整车基本性能的前提下，动力性和经济性能均得到提升。该方法具有通用性，适用于其它混合动力系统、电动汽车系统和其它多目标优化控制领域。

文章仅以传动装置的传动比作为优化变量，后续可将优化模型细化：增加优化变量，例如控制策略的控制参数、动力源参数等；增加目标函数，例如系统成本、排放等，实现对混合动力车型更加全面、多维度的优化分析。