采用CCL/LCC复合谐振网络的电流型ICPT系统

夏晨阳， 路 强， 贾仁海， 张 杨， 张 望， 伍小杰

(1． 江苏省煤矿电气与自动化工程实验室(中国矿业大学)， 江苏省徐州市 221116；2． 国网嘉兴供电公司， 浙江省嘉兴市 314100)

0 引言

感应耦合电能传输(inductively coupled power transfer，ICPT)技术由于其安全、可靠、灵活等优点，自其诞生以来受到国内外学者的广泛关注，并在系统拓扑结构、谐振补偿网络、磁路耦合机构、系统输出特性、系统稳定性等各个方面得到了大量研究，取得了丰硕的成果，进一步推进了产业化进程。目前，ICPT技术已成功应用于手机、家用电器和电动汽车等各个领域，已经成为无线电能传输(wireless power transmission，WPT)的主流技术之一[1-6]。

通常，在感应耦合无线电能传输的实际应用中，用电设备要求在负载变化甚至气隙条件变化时具有恒压输出特性，并保有较好的频率稳定特性。为达到上述要求，目前主要从闭环反馈控制方法[7-10]、新型谐振补偿网络设计[11-19]等方面进行了研究。

通过闭环反馈控制方法实现ICPT系统变负载条件下的输出恒压稳频已有较多研究。其中，为实现ICPT系统输出恒压，文献[7]提出了一种新型的功率补给及自循环模式的输出控制方法，该ICPT系统输出电压恒定。文献[8]采用变频控制来实现恒流和恒压输出。但是变频控制会导致系统无法维持稳频特性。为解决ICPT系统频率稳定性差的问题，文献[9]提出了基于动态无功补偿和静态无功补偿的频率稳定控制方案。文献[10]中提出了采用分段控制输出稳频方法。

虽然这些方法能够较好地实现动态负载下ICPT系统输出电压恒定、系统谐振工作频率稳定，但是为实现多个目标，需要引入多个闭环控制，从而导致系统设计的难度增大，稳定性降低。

因此，为了同时实现多个控制目标又不使系统结构过于复杂，最好的方法是通过系统谐振补偿网络结构的设计来满足上述各控制目标。文献[11]分析S/S补偿网络得到系统在两个不同的频率点能够实现恒压输出。文献[12]分析了S/P补偿网络，该补偿网络可以精确调整输出电压，然而随着松耦合变压器气隙的变化，输出电压增益变化明显。文献[13]设计了T/S型补偿网络，可使得系统的电压增益与负载值无关，且具有单位功率因数输入特性，但电压增益与耦合系数成正比。文献[14]提出了S/CLC补偿拓扑，能够实现恒压输出和单位功率因数输入。双边LCC补偿拓扑能够实现单位功率因数输入，工作频率和输出电流与负载无关，也得到了广泛的研究[15-19]。

分析现有文献发现，许多学者对动态负载条件下的ICPT系统恒压供电和稳频输出做了研究，然而，对于ICPT系统来说，由于磁路耦合机构的灵活性导致气隙经常发生变化。针对气隙变化情况，也已有学者对如何实现系统恒压输出做了研究及探讨。文献[20]将脉宽调制(PWM)+锁相环(PLL)相结合的控制策略应用到S/S补偿系统，保证负载变化时输出电压增益恒定。文献[21]提出利用锁相环控制和恒频控制两种控制策略控制S/SP补偿拓扑以适应负载及变压参数变化。文献[12]针对S/S补偿提出一种自激控制策略，保证系统在负载和耦合条件变化时，输出电压增益固定，但此时系统输入阻抗呈感性，系统控制困难且效率较低。

本文针对现有技术研究的上述不足，提出了一种CCL/LCC复合谐振网络电流型ICPT系统。选择松耦合变压器漏感模型，在采用串联电容补偿原、副边漏感的基础上，选择在原、副边同时加入并联谐振电容来补偿励磁电感，实现松耦合变压器完全补偿。该补偿网络实现了系统输出电压增益与负载值无关，并且实现了系统稳频运行，提高了系统的稳定性。同时，基于分布式电容矩阵，模拟动态调谐技术[22-23]，实现了系统在气隙变化后完全补偿耦合电感，可使得输出电压和工作频率与负载无关。

1 CCL/LCC复合谐振网络ICPT系统

基于松耦合变压器互感等效模型的CCL/LCC复合谐振网络电流型ICPT系统如图1所示。

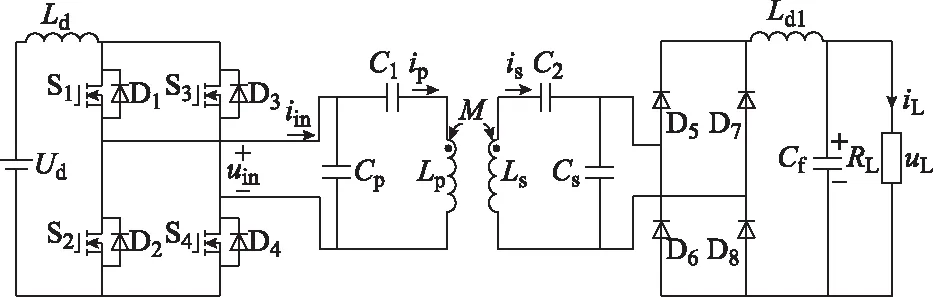
图1 采用CCL/LCC复合谐振网络的电流型ICPT系统结构Fig.1 Structure of current-type ICPT system with CCL/LCC composite resonant network

图1中：Ud为直流电源电压；Ld为输入直流电感；S1至S4为开关管MOSFET；D1至D4为反并联二极管；Lp和Ls分别为发射线圈与接收线圈的自感；M为两线圈的互感；Cp，C1，Lp组成原边CCL复合谐振网络；Ls，C2，Cs组成副边LCC复合谐振网络；整流二极管D5至D8与滤波电感Ld1、滤波电容Cf构成整流滤波电路；RL为负载电阻；ip和is分别为原边发射线圈电流和副边接收线圈电流；uin和iin分别为逆变桥输出电压和电流；iL和uL分别为整流后输出电压和输出电流。

CCL/LCC型ICPT系统能量发射端与能量接收端拓扑对称，通过电路控制与参数设计，系统原边线圈可工作于磁场激发与磁场接收两种模式，能够使能量双向传输。

2 CCL/LCC型ICPT系统参数设计

2.1 输出电压恒定参数设计

高频状态下，线圈的品质因数很高，故忽略线圈的等效内阻。同时，将整流滤波电路整体近似等效为纯阻性负载R=π2RL/8[24]。CCL/LCC复合谐振网络ICPT系统漏感等效模型如图2所示，其中：Lσ1和Lσ2分别为原、副边漏感；Lm为励磁电感；原、副边线圈匝数比为1∶n；io和uo分别为系统等效电阻的电压和电流。

图2 CCL/LCC型ICPT系统漏感等效模型Fig.2 Equivalent model for leakage inductance of CCL/LCC-type ICPT system

根据基尔霍夫电压定律和电流定律，由图2可得输出电压增益如式(1)所示[21]。

(1)

式中：ω为系统角频率；Z1=jωLσ1+1/(jωC1)；Z2=jωLσ2+1/(jωC2)。

定义Z3=jωn2Lm+1/(jωCs)，可将电压增益表达式(1)化简为式(2)。

(2)

式中：

Δ1=(jωCsZ1Z2+Z1-n2ω2LmCsZ1+

jωCsZ2+jωLm)R=jωCsZ1Z2+

jωCsZ1Z3+Z2(Z1+jωLm)R+jωLmR

Δ2=C1C2-n2LmLσ1-LmLσ2-Lσ1Lσ2ω4+

(Lσ1C1+LmC1+n2LmC2+Lσ2C2)ω2-1=

Aω4+Bω2-1

A=-n2LmLσ1-LmLσ2-Lσ1Lσ2C1C2

B=Lσ1C1+LmC1+n2LmC2+Lσ2C2

可以看出，当Δ2=0时，输出电压增益与负载电阻R无关，解方程Δ2=0，得出系统的工作角频率为：

(3)

(4)

在角频率ωH和ωL下工作时，系统输出电压增益分别如式(5)和式(6)所示。

Gv(ωH)=

(5)

Gv(ωL)=

(6)

由式(5)和式(6)可知，若要使输出电压增益值Gv(ωH)和Gv(ωL)与互感参数无关，则必须有下式成立：

Z1Z3+Z2(Z1+jωHLm)=0

(7)

Z1Z3+Z2(Z1+jωLLm)=0

(8)

若要使式(7)和式(8)成立，需使Z1=Z2=0。当满足该条件时，有

(9)

式(9)成立时，则有输出电压增益值为：

Gv(ωH)=n

(10)

Gv(ωL)=n

(11)

由式(9)可知，在负载电阻及磁路耦合机构气隙宽度变化时，只要保证原、副边漏感被完全补偿掉即可实现输出电压恒定。代入完全补偿条件到式(3)和式(4)中，可将工作角频率点ωH与ωL简化为：

(12)

(13)

从上面的分析可以看出：对于一个实际系统，为实现系统输出与气隙无关特性，需要同时满足Z1=Z2=0的条件；且当气隙变化时，为满足Z1=Z2=0条件，需要根据漏感Lσ1和Lσ2的大小，加入电容矩阵，对C1和C2进行动态调谐[22-23]加以实现。

2.2 系统谐振工作频率稳定参数设计

负载动态变化时，系统工作在一定角频率点下系统输入阻抗Zin呈纯阻性，即具有稳频特性。系统输入阻抗Zin表达式如下：

(14)

(15)

由式(15)可知，当变压器原、副边漏感和励磁电感被完全补偿时，其输出电压增益值与负载电阻及磁路耦合机构气隙宽度无关，且同时系统具有稳频特性。角频率ωH与式(15)相对应，可使系统输入总阻抗Zin虚部始终为0，而角频率ωL与式(15)不相对应，所以不能使系统输入总阻抗Zin虚部始终为0。当fH为系统谐振频率f0时，系统输入阻抗Zin的表达式如下：

(16)

由此可知，系统输入阻抗Zin为纯阻性，可降低系统的伏安容量，减少电路损耗，提高系统的效率。在负载变化时，系统谐振频率fH恒定不变，系统可采用恒频控制策略，该控制方式简单，系统的稳定性较好。

2.3 气隙变化适应参数设计

当松耦合变压器被完全补偿时，系统输出电压增益仅与磁路耦合机构匝数比有关，且具有频率稳定特性。然而，在气隙条件变化时，磁路机构的参数相应改变，因此系统需要应用动态补偿技术改变补偿电容使系统重新被完全补偿，以实现气隙变化条件下系统恒压稳频运行，提高系统对气隙变化的适应能力。本系统动态调谐流程如图3所示。

图3 动态调谐流程图Fig.3 Flow chart of dynamic tuning

3 CCL/LCC型ICPT系统特性分析

ICPT系统在气隙距离为10 cm、线圈耦合系数kmin=0.187时，系统参数如附录A表A1所示。为简化分析，松耦合变压器原副边线圈匝数比取为1∶1。

3.1 输出电压恒定特性

为研究系统负载电阻R和输出电压的关系，结合附录A表A1中的参数，画出系统工作在谐振频率20 kHz下输出电压有效值Uo随负载电阻R变化的曲线，如图4所示。

图4 输出电压有效值Uo随负载电阻R变化的关系曲线Fig.4 Curve of valid values of output voltage Uo varying with load resistance R

由图4可知，在系统谐振频率20 kHz处，负载电阻R在0～100 Ω范围内，系统输出电压近似保持不变，输出电压具有较强的负载无关性。

切换不同负载电阻R，输出电压有效值随时间变化曲线如附录A图A1所示。当负载变化时系统输出电压可以维持稳定，与系统参数设计相符。

3.2 零输入相角特性

结合附录A表A1参数画出气隙不变、负载电阻变化时，系统输入阻抗相角θ随频率f变化的曲线，如附录A图A2所示。分析该图中曲线可知，系统工作在fH=20 kHz下，气隙保持不变，负载变化时，系统始终具有单位功率因数输入特性，系统输入阻抗始终呈纯阻性。

基于2014年推出的Finissimo Tourbillon陀飞轮机心，宝格丽全新研发出Calibre BVL 288机心。机心通过在背面安装精美的创新外缘式摆锤为腕表自动上链。圆形摆锤由白金和铝两种密度悬殊的金属材质打造而成，为机心自动上链。机心还采用飞行陀飞轮，配备滚珠轴承系统，有效削减厚度。

3.3 气隙变化适应特性

结合附录A表A1系统参数,在气隙变化为8 cm和5 cm时，重新对系统进行补偿。在气隙为8 cm 时，线圈互感M=28.67 μH，耦合系数kmid=0.254，通过计算得出谐振网络电容分别为Cp=1.105 μF，C1=0.75 μF，C2=0.75 μF，Cs=1.105 μF。在气隙变为5 cm时，互感变为M=42.29 μH，耦合系数kmax=0.375，计算得出谐振网络电容分别为Cp=0.75 μF，C1=0.9 μF，C2=0.9 μF，Cs=0.75 μF。

气隙变化后不重新进行补偿时输入阻抗相角θ随系统频率变化曲线如附录A图A3(a)所示。气隙变化后重新完全补偿时输入阻抗相角θ随系统频率变化的曲线如附录A图A3(b)所示。

分析附录A图A3中曲线可知，系统工作在fH=20 kHz下，气隙变化，负载保持不变时，不完全补偿时系统输入阻抗相角不为零。改变补偿电容，完全补偿时系统输入阻抗相角等于零，此时系统具有单位功率因数输入特性。

绘制气隙变化情况下输出电压有效值Uo随频率f变化的曲线如附录A图A4所示。由该图可知，当松耦合变压器气隙距离变化后，保持谐振网络补偿电容参数不变，系统输出电压发生较大改变。而利用动态调谐技术将耦合电感完全补偿，系统输出电压能够保持稳定。

3.4 系统效率特性

当系统恒定工作在谐振频率下时，系统输出功率Pout如下：

(17)

式中：Rp为原边线圈内阻；Z2=1/(1/R+jωCs)+1/(jωC2)+jωLs+Rs，其中Rs为副边线圈内阻；Zr=(ωM)2/Z2；Io为系统输出电流有效值。

系统传输网络总损耗Ploss为：

(18)

式中：Ip和Is分别为原边发射线圈电流和副边接收线圈电流有效值，Ip=Uin/Zr+jωLp+Rp+1/(jωC1)，Is=ωMUin/Zr+jωLp+Rp+1/(jωC1)Z2。

推导出系统传输网络效率ηp为：

(19)

根据式(19)和附录A表A1系统参数可作出如图A5所示的系统传输网络效率随负载电阻变化的曲线，如附录A图A5所示。由图A5可知，负载电阻R在0～100 Ω范围内，系统传输网络效率ηp首先随着负载电阻R增大而显著增大，当负载电阻R继续增大时，效率会缓慢下降。该系统在仅以负载电阻R为变量，其余参数确定的情况下，系统传输网络存在一个最优负载点，可实现最大效率传输。

4 实验验证

为验证理论分析的正确性，根据图1及附录A表A1所示参数搭建如附录A图A6所示CCL/LCC型复合谐振网络ICPT系统实验平台。为简化实验，实验中采用模拟动态调谐技术，根据理论计算，通过手动改变电容补偿参数进行动态补偿。

4.1 电压增益的负载特性

首先，选取气隙宽度为10 cm，即松耦合变压器耦合系数kmin=0.187的一组参数进行实验验证。实验测得驱动电压ugs与逆变器输出电压uin的波形如附录A图A7所示。由该图可知，驱动电压与逆变器输出电压保持同相位，驱动电压在逆变器输出电压过零点控制开关管的开通与关断。这表明系统可以实现零电压开关。

当松耦合变压器耦合系数kmin=0.187，负载电阻为25 Ω和50 Ω时系统输出电压uo的稳态波形分别如附录A图A8和图A9所示。负载电阻由25 Ω突变至50 Ω过程中系统输出电压uo和输出电流io波形如附录A图A10所示。由图可知，当负载变化时，系统输出电压具有恒定特性。

4.2 系统频率稳定特性

在松耦合变压器耦合系数kmin=0.187，负载电阻为25 Ω和50 Ω时系统逆变器输出电压uin与输出电流iin波形如附录A图A11和图A12所示。

由式(13)和式(14)可知，系统存在2个使输出电压恒定的工作频率点。根据式(15)可知，只有系统工作在ωH对应的频率下才能使系统输入阻抗呈纯阻性。附录A图A11和图A12在不同负载电阻下输出电压保持不变且逆变器输出电压uin与输出电流iin都保持同相位，系统输入阻抗为纯阻性。因此，系统负载切换前后均工作在谐振频率下，系统频率稳定。

4.3 气隙变化适应特性

根据附录A表A1的系统电路参数，画出气隙宽度变化下变压器漏感和励磁电感被完全补偿以及补偿电容不变、未完全补偿情况下，输出电压随负载电阻变化的曲线，如图5所示。

图5 不同负载下输出电压值Fig.5 Output voltage values under different loads

由图5可知，当气隙宽度确定时，即松耦合变压器耦合系数k值确定的情况下，观察系统输出电压与负载关系，证明了CCL/LCC型复合谐振网络ICPT系统输出电压恒定。同时，在耦合机构条件变化即耦合系数k值不同时，若系统被完全补偿，系统输出电压变化较小。若补偿电容保持不变，输出电压降出现较大跌落。因此，CCL/LCC型复合谐振网络ICPT系统在变气隙条件变化时，若利用调谐技术实现完全补偿，可以实现输出电压恒定。

4.4 系统效率分析

传输网络的损耗是ICPT系统损耗占比最大的一部分，逆变器等其他损耗虽然所占比重较小，但也不能忽略不计。因此，本文使用Ainuo公司的AN87500多通道功率分析仪测试气隙10 cm这一组参数下的整机效率。系统参数如附录A表A1所示，绘制如图6所示的效率曲线图。

图6 系统整体效率η随负载电阻R变化的曲线Fig.6 Curve of overall system efficiency η varying with load resistance R

由图6可以看出，此CCL/LCC复合谐振网络电流型ICPT系统效率首先随着负载电阻增加而提高，随着负载电阻继续增大，系统效率又会降低，因此系统存在最优负载点，可实现系统最优效率传输。但实际测试的系统整机效率低于计算效率，是因为实际电路参数误差和元器件寄生参数的影响。

5 结语

根据恒压型ICPT系统的设计需求，本文提出了采用CCL/LCC复合谐振网络的电流型ICPT系统。CCL/LCC复合谐振网络完全补偿时具有输出电压恒定、系统工作频率稳定的特性。同时，通过动态调谐技术，实现了系统在气隙变化条件下的恒压稳频输出。结合实际参数搭建了实验平台，实验结果证明了CCL/LCC型复合谐振网络ICPT系统的良好特性。

使用动态调谐技术会使系统体积庞大且控制复杂，下一步将继续深入研究改进。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。