静基座捷联罗经初始对准方法
张伟,付泳
(1 中国电子科技集团公司第二十研究所,西安 710068;2 火箭军驻燕山电子设备厂军代室,北京 100192)
0 引言
初始对准是捷联惯性导航系统进行导航的前提,捷联惯导系统的初始对准主要是提供捷联惯导的导航解算所需要的初始姿态矩阵[1]。初始对准的结果直接影响惯性导航系统的导航精度。所以,对捷联惯性导航系统进行初始对准是十分必要的。进行初始对准的方法很多,如多位置对准法和罗经对准法、卡尔曼滤波最优估计对准方法、传递对准法等[2]。
其中,罗经法初始对准是平台惯导系统(PINS)的经典对准方法[3],罗经对准法可分为水平调平和方位对准两个步骤,方位对准在水平调平的基础上进行。PINS中实体平台具有隔离外界干扰的作用,因而平台罗经能够实现晃动基座下的初始对准。捷联惯导系统(SINS)本质上与平台惯导系统相同,所以,在SINS初始对准中也可以根据平台罗经初始对准的特点,以数学平台代替物理平台,采用罗经对准方法,本文主要介绍静基座下的罗经对准方法。
1 捷联罗经初始对准原理及算法
在捷联惯性导航系统中以数学平台替代平台惯导中的物理平台,数学平台如图1所示,图中为起数学平台的作用的姿态矩阵,为陀螺测量值,为加速度计测量值,ωc=[ωcEωcNωcU]T为控制角速率;为地球自转角速率。经姿态矩阵变换到导航坐标系下的
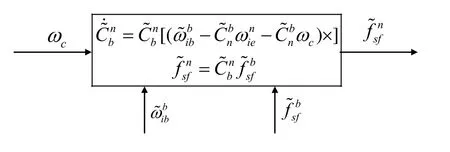
图1 捷联惯导数学平台
参照平台惯性导航系统罗经初始对准原理框图,以数学平台代替实体平台便构成的捷联罗经对准的通道。东向通道如图2所示,其中去掉数学平台的部分为平台罗经对准原理的控制规律。

图2 捷联罗经水平对准东向通道
从图2中可以得到东向通道控制规律:
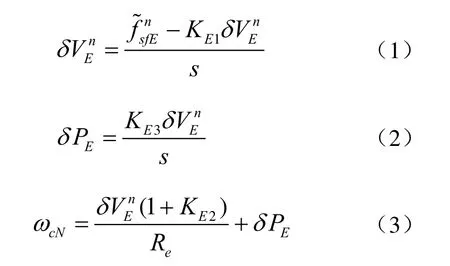
如果捷联数学平台的更新时间sT足够短,可以直接用一阶差分近似代替微分,将式(1)~式(3)分别离散化为式中,k=1,2,3...。
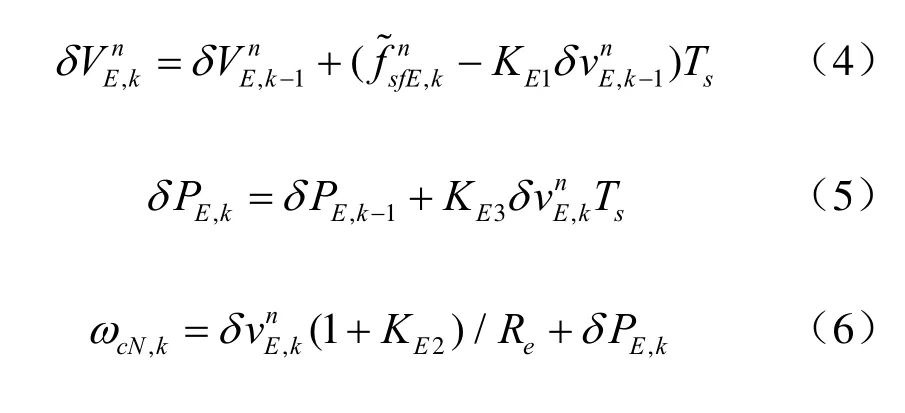
同理,构成捷联罗经水平对准的北向通道图3,构成捷联罗经方位对准图4。
图2、图3和图4中:Kij(i=E,N,U;j= 1 ,2,3,4)为控制回路的调节参数,由于三阶水平对准回路的对准精度不受Kij的影响,所以根据对准的收敛速度来选取调节参数,一般东向水平对准通道调节参数典型取值如下[4](北向水平对准通道调节参数选取同东向水平对准通道):

式中:σ为衰减系数,ξ为阻尼比,为舒拉频率,阻尼比一般选取(下同),然后根据对准精度、时间和环境干扰等因素调整衰减系数σ。其中当时,为阻尼振荡周期。
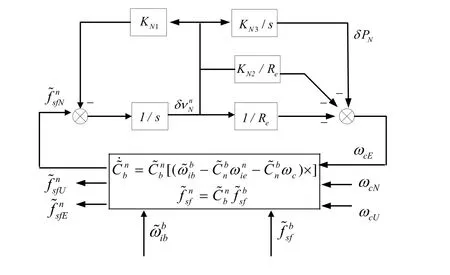
图3 捷联罗经水平对准北向通道
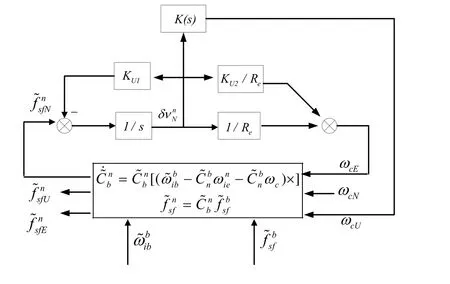
图4 捷联罗经方位对准
方位对准通道调节参数典型取值如下:

并将图3中的控制规律离散化为式(7)~式(9):

图4中的控制规律分别离散化为式(10)~式(12):

将捷联数学平台也按更新周期sT离散化成式(13)、式(14)。由式(4)~式(14)便构成了完整的捷联罗经初始对准算法。

2 捷联罗经初始对准步骤
捷联罗经初始对准它可分为以下三个步骤:
(1)方位角未知情况下水平对准
在方位角未知情况,可以将它的初始值假设为零,在静基座初始对准过程中两个水平姿态角一般不大,初始值也设为零。再利用图2和图3两个通道一起构成水平对准方案。静基座条件下可将地球自转角速率作为陀螺常值漂移,通过罗经水平通道原理可知,陀螺常值漂移不影响水平对准的精度,对准精度由加速度计零偏误差决定[5]。
(2)粗略方位对准

然后对大方位误差角条件下的SINS非线性误差方程进行化简,静基座下忽略水平姿态误差角、陀螺漂移和加速度计零偏等次要因素的影响后,近似如下:
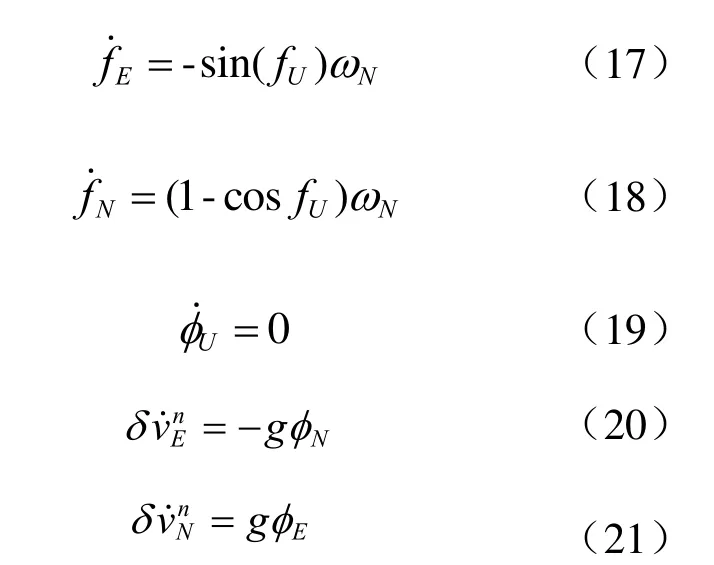
将式(20)和式(21)再次微分,并将式(17)和式(18)带入,建立速度误差与大方位误差角φU之间的关系:
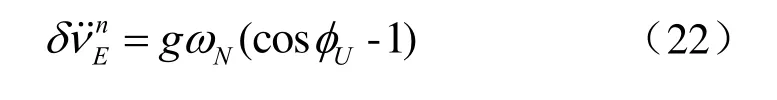
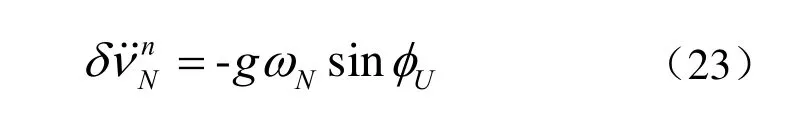
在φUt时刻由式(22)、式(23)二次积分后,可以粗略求得方位误差的三角函数表达式如下:
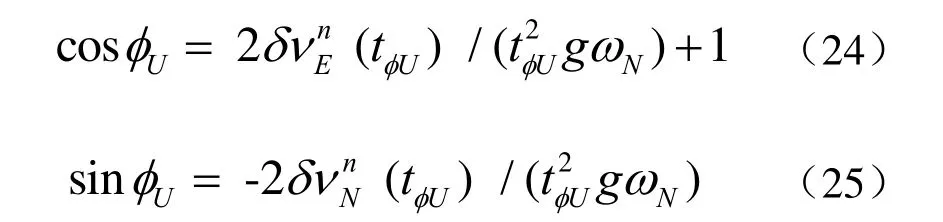
据此,很容易构造修正矩阵:
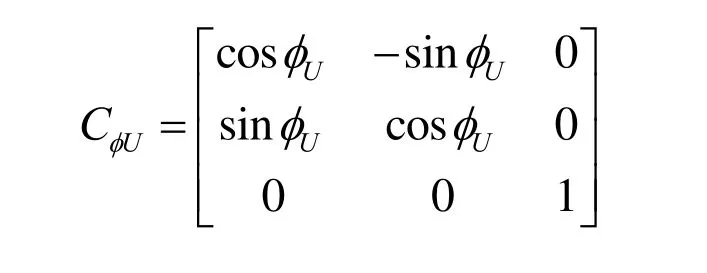
利用式(26)对φUt时刻姿态矩阵作修正,便实现了捷联罗经的粗略方位自对准,获得粗略姿态矩阵
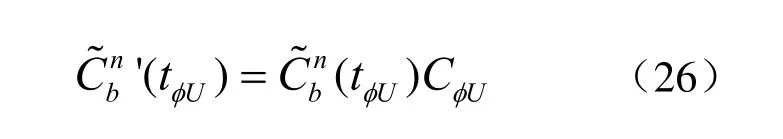
(3)罗经方位对准
在进行罗经方位对准前,可以再进行一次水平对准,因为在方位粗对准过程中水平误差角有可能变大。具备粗略方位和精确水平对准后,利用水平东向通道算法和罗经方位对准算法就可以完成整个捷联罗经初始对准过程。
3 仿真分析
采集激光惯组置于转台,采样周期 8ms;共 6列数据前3列为角增量(当量0.932角秒/脉冲),后3列为速度增量(当量500*gsμ/脉冲);陀螺常值漂移0.01/h°,随机游走系数加速度计常值漂移 100μg,加速度计随机游走系数初始姿态[1° 2° 3 0°],依次为俯仰、横滚和航向。采用上面介绍的捷联罗经对准方法对准结果如图5、图6所示。从图5、图6中可以知道,水平对准的收敛速度要快于方位对准,对准误差也较方位对准小,对准后的方位误差大概在 3'(0.05°)。其他方位角对准结果如表1所示。

图5 捷联罗经初始对准结果曲线

图6 捷联罗经初始对准误差曲线
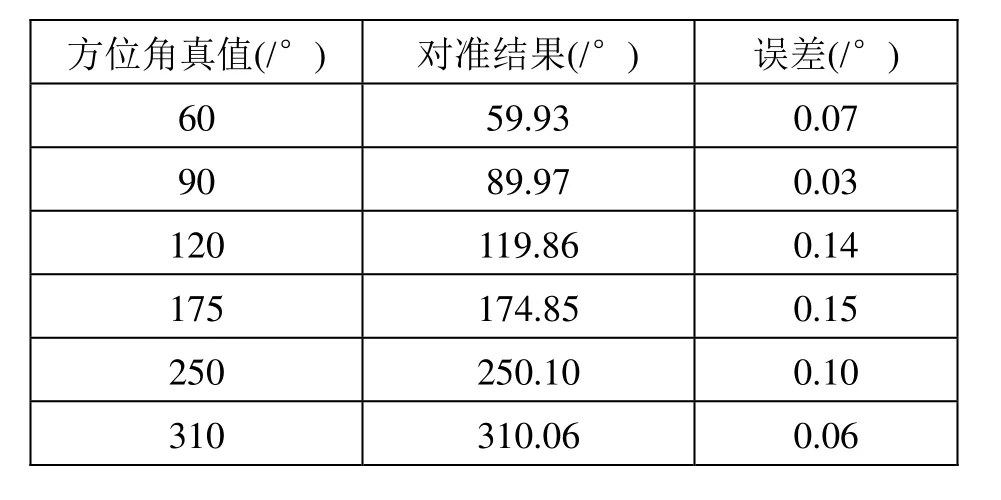
表1 不同方位角初始对准仿真结果
4 结论
本文从分析平台罗经初始对准的原理出发,提出了捷联罗经初始对准的原理并给出了离散化公式,与平台罗经对准过程不同的是,借助于大方位误差条件下的非线性误差简化方程,建立静基座SINS速度误差和方位误差角的关系,最后得到方位误差角。最后,通过仿真分析验证了捷联罗经初始对准算法有效。

