基于最小二乘拟合的雷达航迹匹配算法

王丽华，任磊，李斌，王枭雄

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

雷达作为一种有效的目标探测设备而被广泛使用，受其技术发展水平的限制，在目标机动等情况雷达输出的目标航迹信息可能不够完整和精确。在雷达仿真模拟系统中，多平台多目标环境下，雷达输出的目标航迹点与目标真实航迹信息的正确匹配是有效评估雷达航迹信息处理算法性能的前提。

常用的雷达航迹匹配算法是基于单点信息对雷达目标航迹与目标真实航迹是否匹配进行判断[2-4]，若该点是野值点，或发生信息缺失、目标偏航、目标机动等情况，则会产生错误匹配结果。本文采用的基于最小二乘拟合的雷达航迹匹配算法，是基于雷达输出目标航迹和目标真实航迹两个点集的关联匹配，可以降低匹配结果对单点信息的依赖程度，提高雷达航迹与真实航迹的匹配正确率。

1 最小二乘曲线拟合

为降低雷达航迹匹配结果对单点信息的依赖程度，提高雷达航迹匹配正确率，本文采用的雷达航迹匹配方法是基于两个点集的关联匹配，一个点集为雷达融合点迹，另一个点集为仿真系统规划的目标真实点集。

最小二乘法作为一种重要的统计优化技术，是众多数理统计学分支的理论基础，其通过最小化误差的平方和来确定一组数据的最佳预设函数匹配。雷达输出的目标点迹，由于噪声等多种因素的影响，量测点随机分布在真实航迹的周围，在大样本条件下，通常分布是对称的。因此，将最小二乘法应用于航迹拟合处理中，可去掉由噪声等因素产生的随机波动，使航迹更加平滑，更直观地反映出目标的运动趋势。本文采用最小二乘多项式拟合方法拟合雷达航迹和系统仿真航迹[1]。

对于给定数据点集｛(xi,yi)｝(i= 1,2,…,m)，首先设定n(假定m>n)次多项式Pn(x)为：

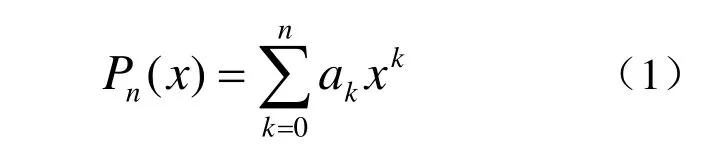
那么多项式Pn(x)需满足

方便计算，考虑显然上式成立的解ak(k=1,2,…,n)即为最小二乘拟合的解。根据求极值的方法，对a0,a1,a2,…an分别求偏导，再使偏导为零，得到如下方程组[5]：

整理后得到：

解此方程组就能得到所需要的参数a0,a1,a2,…an，代入Pn(x)即可得到最小二乘拟合多项式。

图1 最小二乘拟合空间曲线

仿真系统中雷达航迹数据点集包括时间ti和目标坐标｛ti,(xi,yi,zi)｝(i= 1,2,…,m)，将坐标点集在x,y,z三个方向上分别进行最小二乘曲线拟合，再对时间进行插值得到拟合后坐标点集 (xj,yj,zj)，再将坐标点转化为地理坐标系。最小二乘拟合空间曲线仿真图如图1所示，为体现运动轨迹随时间变化规律，图中三维坐标分别为经度、纬度和时间。

2 欧几里得距离

仿真系统中有多个目标平台，需将接收的雷达航迹与仿真中的目标真实运动轨迹相关联，本文采用计算欧几里得距离的方法判断两条航迹的关联度。欧几里得距离是在m维空间中两点之间的真实距离，三维坐标中两点 ),,(111zyx和 ),,(222zyx的欧几里得距离公式：

将上节中拟合的空间两条曲线按照时间间隔Δt进行插值得到雷达航迹点集｛tk,(xtk,ytk,ztk)｝(k= 1 ,2,…,l)和目标真实运动轨迹点集｛tk,(xsk,ysk,zsk)｝(k= 1 ,2,…,l)，两点集中相同时间坐标点计算欧几里得距离，得到距离点集｛tk,dk｝(k= 1,2,…,l)：

两条航迹相关联判定条件：欧几里得距离点集的平均值Avg与Std之和小于等于距离门限阀值T：

3 仿真验证分析

仿真系统为多平台多目标仿真场景，仿真系统模拟输出目标的真实运动轨迹，外部设备反馈给仿真系统目标的雷达融合航迹。轨迹匹配算法用于雷达融合航迹与仿真系统模拟目标的真实轨迹进行相关匹配，最终在地图上显示出相关联的雷达融合航迹和目标真实模拟轨迹。

航迹匹配算法主要包括以下5部分内容：

（1）仿真系统模拟目标运动真实轨迹曲线拟合；

（2）目标雷达融合航迹曲线拟合；

（3）相同时间段内对分别对拟合曲线进行插值，取得插值点迹的坐标（X，Y，Z）；

图2 算法流程图

（4）计算两组插值点迹的欧几里得距离集合；

（5）计算距离集合的均值和标准差，根据门限阀值判断航迹是否匹配。

算法工作流程图如图2所示。

图3 仿真系统航迹匹配正确率统计界面

如图3所示，为仿真系统的航迹匹配正确率统计界面，仿真系统剧情模拟4个平台200批目标，统计时间为100s，航迹匹配正确率为99.6%。

4 结论

本文针对仿真系统多目标平台时，雷达输出目标航迹与目标模拟真实航迹相关联匹配算法，采用最小二乘多项式拟合方法，拟合目标航迹曲线后再对拟合曲线插值计算欧几里得距离，根据一定的判定条件计算关联匹配结果，克服了单点信息在存在野值点或信息缺失和目标机动等情况时出现错误的关联匹配结果，提高了雷达输出目标航迹与模拟真实航迹关联匹配正确率。本算法已应用在实际工程中，并在工程应用中设置不同的仿真场景，验证航迹关联匹配正确率，实际测试结果显示本算法具有良好的使用效果。