基于FPGA的高速并行滤波器设计与实现

文明

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

随着近年来通信技术的快速发展，在个人通信、军事通信领域对宽带大容量信息传输的需求持续增加。比如，移动通信领域中高清多媒体业务的高速传输需求以及军事侦察领域中 SAR图像、高清视频等信息的实时传输需求等。因此，未来无线通信将需要数百 Msps到数 Gsps的传输带宽以及数Gbps到数十Gbps的信息传输速率。

目前高速通信系统的实现主要是通过可编程技术，在FPGA上实现信息的编译码、基带信号的调制解调、成形滤波等。从FPGA实现的方面考虑，为提高FPGA内部复杂算法工作的稳定性，并减小FPGA布局布线的复杂度，最好将FPGA的主时钟设计在100MHz左右。因此，对于1Gsps左右的高速率数据传输的处理需要采用并行处理结构，以此来减小对FPGA工作频率的约束。但是，并行路数越多，硬件实现复杂度越高，所以需要在资源和速度方面进行折中考虑。

本文研究基于FPGA的1Gsps符号速率下的高速并行滤波器设计与实现问题。首先分析影响滤波器性能的主要参数，并进行仿真分析，然后研究并行滤波器的实现方法，包括时域并行滤波方法和频域并行滤波方法，提出了高速通信系统（≥1Gsps）发射端和接收端成形滤波器的设计结构，最后在FPGA上验证了该结构的有效性。

1 高速滤波器设计

升余弦滤波器广泛应用于基于PSK和QAM调制方式的通信系统中，它属于满足奈奎斯特准则的脉冲成形滤波器。对于采用升余弦滤波器的通信系统，在滤波器输出信噪比最大的时刻进行判决，可以得到最小的差错概率。升余弦滤波器的传递函数为[2]

其中，f为信号频率，α为滚降因子，Ts为符号周期。

在实际应用中，升余弦滤波器可以在发射端和接收端使用同样的滤波器来实现。在发射端滤波器可以限制发射信号的带宽，减小相邻信道间的干扰；在接收端可以滤除带外噪声。

在滤波器的设计中，需要分析滤波器的各个参数滤波器性能的影响，并进行权衡取舍，选择合适的滤波器参数。对于本文采用的根升余弦滤波器，其主要参数为滚降因子α、滤波器阶数，在具体实现中需要考虑滤波器系数的量化位数对滤波器性能的影响。

α的取值范围为0到1，对于0α=，升余弦滤波器对应于具有最小带宽的矩形滤波器，但它是物理不可实现的，随着滚降因子α的增加，在时域上，幅度在增大，相邻符号间隔内的时间旁瓣减小，如图1所示；在频域上，滤波器的主瓣带宽在增大，第一旁瓣的衰减也同时增加，如图2所示。

图1 不同α情况下的滤波器冲激响应图

滤波器阶数与通带及阻带的衰减有关，阶数越高，滤波器的通带越平、阻带衰减越大以及过渡带越窄，如图3所示，但同样地，滤波器阶数越高，滤波器的群时延也就越大，使得系统更容易受到定时抖动的影响。

图2 不同α情况下的滤波器幅频响应图

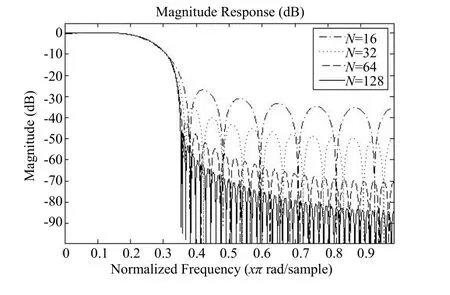
图3 不同阶数滤波器情况下的滤波器幅频响应图

图4 滤波器系数在不同量化情况下的幅频响应图

在滤波器的实现结构中，由于FPGA在处理定点数运算方面的优势，需要对滤波器系数进行量化，考虑到有限字长效应，量化的位数越多，滤波器的通带越窄，阻带的衰减越大，其幅频响越接近于浮点数时的情况，如图4所示；但同样地，量化位数越多，需要的运算逻辑资源也就越多。

2 高速滤波器的FPGA实现

2.1 高速调制解调系统架构

由于受器件最高工作频率限制，基于FPGA的串行处理速度无法实现1Gsps符号速率的信号实时处理，因此需采用并行处理的方式来降低每条路径上的时钟频率要求。并行路数越多，所需的计算量也就越大。

表1 ≥1Gsps符号速率下不同并行路数比较（fs = 4/Ts ）

根据表1中的分析，可采用32路并行处理的方式实现1Gsps符号速率的数据传输。因此，对于实现1Gsps符号速率的通信调制解调系统示意图如图5所示。

图5 高速通信调制解调系统框图

系统中采用α=0.4，阶数为32的根升余弦滤波器作为发射端和接收端的成形滤波器。

2.2 并行滤波器实现结构

对于并行成形滤波器结构的设计可采用时域与频域两种方式实现。

多相滤波结构是多速率信号处理中抽取滤波器和插值滤波器最常用的时域实现结构。通过该结构可以大大降低对处理速度的要求以及运算的复杂度[1]。因此，可采用多相滤波结构进行发射端和接收端升余弦滤波器的设计，其中：

FIR滤波器一般都是用线性卷积实现的，而线性卷积可以通过基于FFT的频域滤波实现，因此，可采用频域滤波结构来进行发射端和接收端升余弦滤波器的设计。首先，分别计算输入序列、滤波器系数的FFT，然后相乘，最后通过IFFT即可得到卷积结果。

2.3 发射成形滤波器实现

实际中，通信系统的发射端需要对调制信号进行升采样，经过正交调制后转换成模拟信号发射出去，而接收端则需要在符号定时同步后对接收信号进行降采样，以满足解调的要求。

结合上文的分析，1Gsps系统的发射端可采用8路并行的方式进行滤波。首先将滤波器系数进行4倍抽取得到4路的多相滤波器系数，然后每一路输入的调制符号分别经过 4个分解后的多相滤波，最后得到 32路的滤波后数据。具体的实现结构框图如图6所示。该滤波器实现结构一共需要(9+8×3)×8×2次实数乘法，(8+7×3)×8×2次实数加法。

同样地，发射成形滤波器也可采用频域滤波方式实现。由于滤波器的输入信号序列是连续的，而滤波器系数是有限长的，因此，可采用重叠保留法对信号进行分段处理，即将N点的输入序列按长度分成每一段与前(M- 1 )个样本重叠，保留最后(N-M+ 1 )个输出样本，最后将这些输出串接成一个序列即可得到滤波输出结果。

图6 发射端时域并行滤波结构示意图

具体地，一个调制符号经过4倍上采样后的32路数据，经重叠保留后变为64路，再经过64点并行FFT运算、乘以频率滤波器系数，最后经过并行IFFT，选择其中的 32路输出数据即可得到滤波结果，如图7所示。其中，64点并行FFT可采用基-4的蝶形实现，以减少FFT实现级数及运算量，具体的实现结构框图如图8所示；其中基-4的蝶形的实现结构如图9所示。因为=1，所以每个蝶形运算包含3次复数乘法和12次复数加法。该滤波器实现结构一共需要48×4+64次复数乘法，12×16×5次复数加法。其中一次复数加法可以通过两次实数加法实现，一次复数乘法可以通过三次实数乘法和三次实数加法实现。

图7 发射端频域并行滤波结构示意图

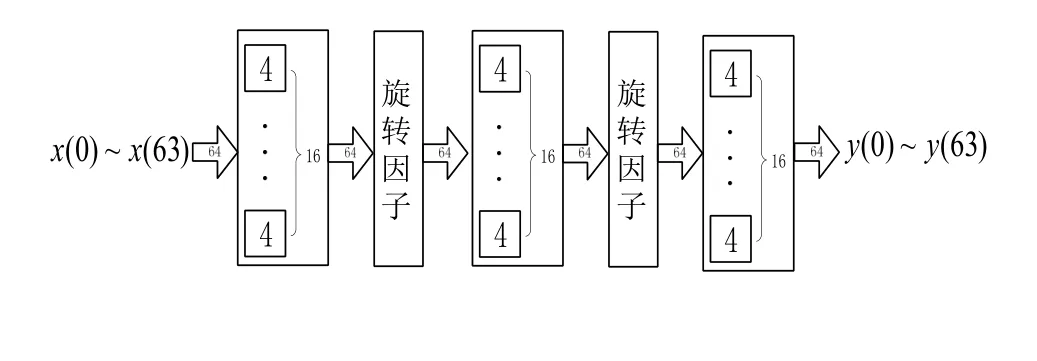
图8 基-4的64点并行FFT实现结构示意图

因此，通过在实现复杂度方面对比，在发射端更适合采用时域并行多相滤波结构实现根升余弦滤波器。

图9 基-4的FFT蝶形实现结构

2.4 接收成形滤波器实现

在接收端，考虑到系统需要在滤波后进行符号定时同步，找到接收符号的最佳采样点，所以需要将 32路输出数据全部保留，在定时同步后再进行数据降采样。因此，接收端时域滤波方法应采用原始滤波器系数进行滤波，并行路数为 32路，而不采用多相的方式实现。具体的实现结构框图如图10所示。该滤波器实现结构一共需要(33+32×3)×32×2次实数乘法，(32+31×3)×32×2次实数加法。

图10 接收端时域并行滤波结构示意图

与发射端的频域滤波器类似，在接收端对于每次输入的32点信号序列，与前一时刻输入的32点信号序列拼接成一个64点信号序列，然后进行64点的并行FFT计算，并与频域滤波器系数相乘，最后经过64点的并行IFFT并舍弃其中的32点，即可得到输入信号的滤波结果。具体的实现结构框图如图11所示。考虑到输入数据为0、旋转因子为1的情况，简化后需要48×4+64次复数乘法，3×64×6次复数加法。

因此，考虑到实现复杂度，在接收端采用并行频域滤波结构实现根升余弦成形滤波器。

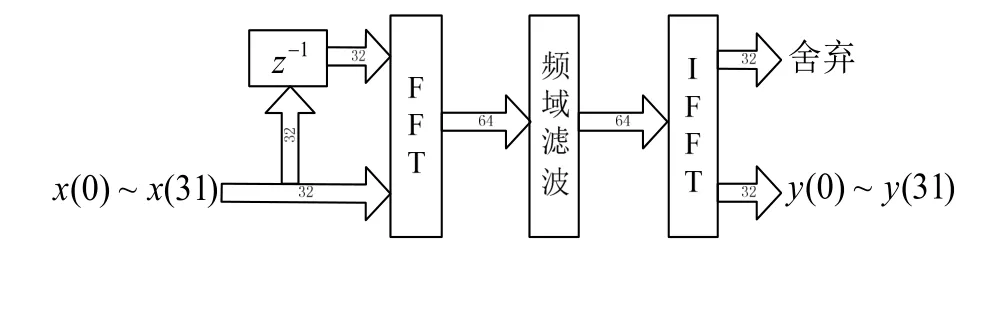
图11 接收端频域并行滤波结构示意图

2.5 滤波器实现结果分析

对基于FPGA实现的滤波器的系统误码率性能进行分析。调制方式采用QPSK，信道为加性高斯白噪声信道。发射端采用时域并行多相滤波方式实现，接收端采用频率并行滤波的方式实现。

在实现中对滤波器系数在时域和频域分别进行 18bit量化。在滤波器的实现运算过程中对输入输出数据和中间结果数据进行截位，发射端滤波器的输出以及接收滤波器的输入数据保留 10bit有效位，便于与10位以上的A/D、D/A进行数据交互；在发射端对中间数据保留13bit有效位，在接收端，对中间结果保留11bit有效位。

具体实现系统在理想无噪声情况下的接收端滤波器输出信号的星座图如图12所示。

图12 基于FPGA实现的滤波器输出信号星座图

分别对发射端的输出信号叠加不同程度的噪声，统计对比理论仿真的误码率和FPGA实现的误码率，具体结果如图13所示，图中横坐标为信噪比SNR(dB)，纵坐标为误比特率BER。

图13 基于理论仿真与FPGA实现的滤波器的调制解调系统误码率结果

从图13中可以看出，采用基于FPGA实现的成形滤波器的调制解调系统在不同信噪比情况下的解调输出误码率结果与理论仿真结果基本一致，证明了该滤波器实现结构的有效性。

3 结论

本文分析了高速调制解调通信系统的成形滤波器的设计和实现问题，通过针对发射端和接收端的特点，设计并实现了基于多相分解的高速并行滤波器和基于频域滤波方法的高速并行滤波器，仿真和实现结果证明了该方法的有效性。该滤波器结构可广泛应用于≥1Gsps的调制解调系统中，同时接收端采用的并行频域滤波结构便于与采样定时同步、频域均衡算法相结合，具有非常好实际应用价值。