钢框架双钢板内填混凝土剪力墙结构滞回性能试验研究

赵宝成，孙筱玮，胡团结，顾 强

(苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011)

钢框架结构抗侧刚度小，为了提高钢框架的抗侧刚度，可在钢框架内填双钢板混凝土剪力墙，形成钢框架双钢板内填混凝土剪力墙结构(steel frame with steel-concrete-steel composite shear walls，简称“SFSCSW”).其中双钢板剪力墙是在剪力墙的两侧设置钢板，采用栓钉或加劲板将双钢板连接起来，内部添加混凝土，外部钢板与内部混凝土共同受力，抵抗水平荷载.施工阶段，外侧钢板可作为混凝土的模板，施工方便.使用阶段，外侧钢板约束内侧混凝土，提高混凝土的变形能力.混凝土内填于钢板之中，可有效防止外侧钢板过早屈曲，提高组合剪力墙的整体刚度及变形能力，使得结构的抗震性能大幅度提高.

近年来国内外对内填混凝土双钢板组合剪力墙滞回性能、力学性能、变形能力进行了试验研究和有限元模拟，验证了内填混凝土双层钢板组合剪力墙承载能力高、延性好、抗震性能优越等优点.Emori[1]进行了l/4缩尺模型的双层钢板内填混凝土剪力墙抗压和抗剪性能试验；Khandaker M.A.Hossain[2]试验研究了采用对穿螺栓双钢板内填混凝土剪力墙在轴向力作用下的力学性能；聂建国等[3-4]进行了钢板内侧焊接栓钉的双钢板内填混凝土组合剪力墙拟静力抗震性能试验，研究了该类剪力墙结构的受力机理；朱立猛等[5-7]试验研究了采用对穿拉杆连接的双钢板内填混凝土组合剪力墙试件的滞回性能，分析了不同设计参数对试件抗震性能的影响；Siamak Epackachi[8]试验研究了双钢板同时采用对穿拉杆和钢板内侧焊接栓钉构造的内填混凝土组合剪力墙的滞回性能.

李盛勇等[9]对外包多腔钢板内填高强混凝土组合剪力墙进行试验研究；李健等[10]试验研究了钢板内侧焊接栓钉及连接板等不同构造形式的双层钢板内填混凝土组合剪力墙的滞回性能和极限承载能力； Link、韦芳芳等[11-12]应用有限元软件分析了双钢板内填混凝土剪力墙的的抗震性能；马晓伟等[13]分析了剪力墙构件的弯矩-曲率曲线以及压弯相关关系，进行了压弯承载力计算；胡红松等[14]提出了双钢板内填混凝土剪力墙基于位移的设计方法，给出了双钢板混凝土组合剪力墙的轴压比限制.

由现有研究成果可知，目前试验研究和有限元模拟主要针对的是单层单跨双钢板内填混凝土剪力墙结构，未考虑周边钢框架与双钢板内填混凝土剪力墙共同作用.为了揭示钢框架双钢板内填混凝土剪力墙结构在循环荷载作用下的破坏模式，设计了1榀单跨2层半1/3缩尺SFSCSW试件，研究了试件在循环荷载作用下的破坏模式、变形能力、耗能能力，得到了试件的滞回曲线、骨架曲线、刚度退化曲线、承载力降低系数曲线、延性系数以及剪力墙的剪切变形等，结果可供相关研究参考.

1 试验概况

1.1 试验设计

钢框架双钢板内填混凝土剪力墙结构为单跨2层半，试件总高3 m.试件跨度为1.2 m，层高为1.2 m.框架柱为HW150×150×7×10，框架梁为HM148×100×6×9，均采用热轧H型钢.双钢板与梁柱焊接，钢板的厚度为3 mm，墙厚60 mm，双钢板之间采用4道加劲板连接，与钢板同厚.试件几何尺寸见图1.

钢材实测的力学性能见表1.留有混凝土标准试块3个试样，立方体抗压强度平均为21.08 MPa.

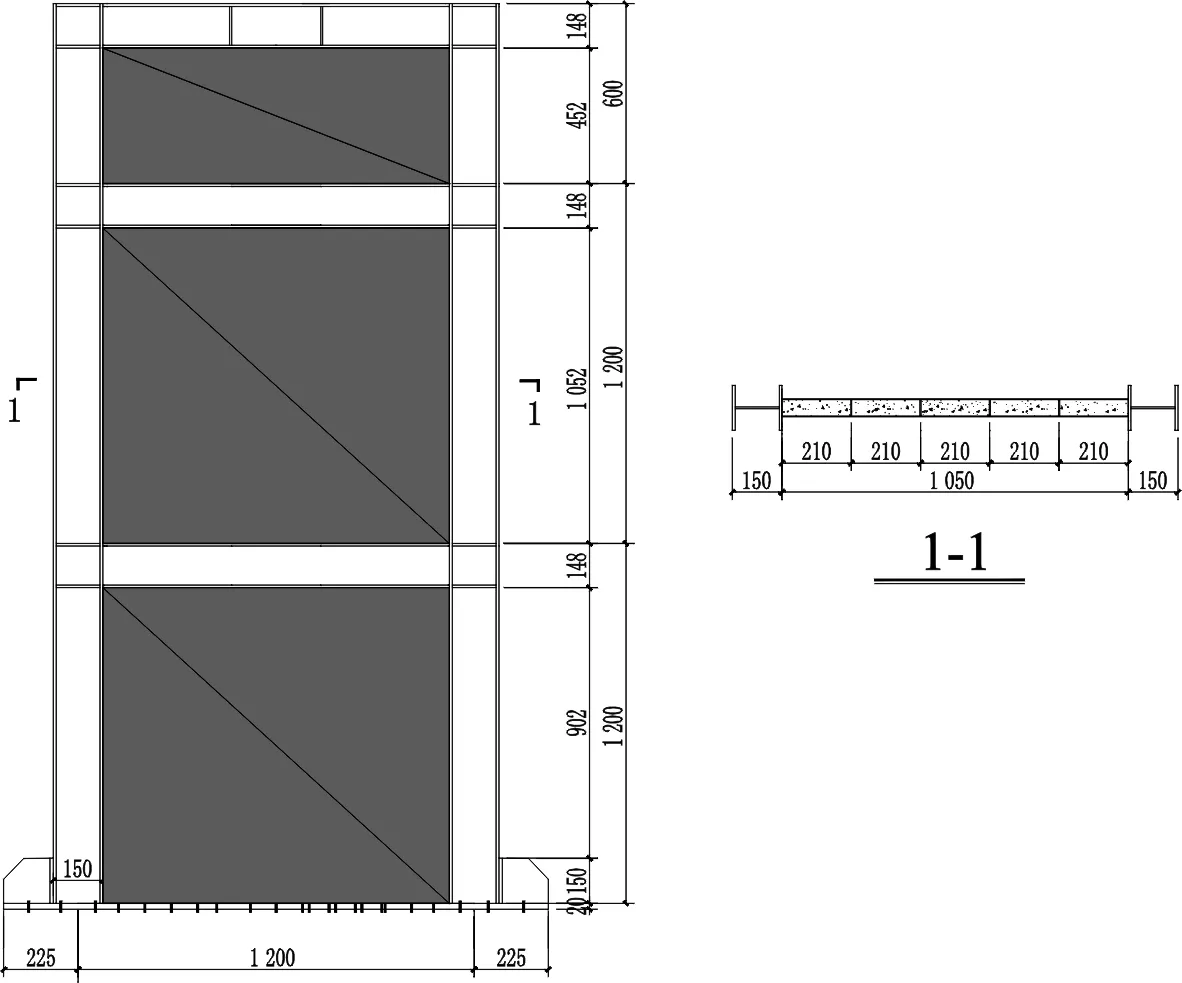
图1 试件几何尺寸Fig.1 Geometry dimension of test specimen

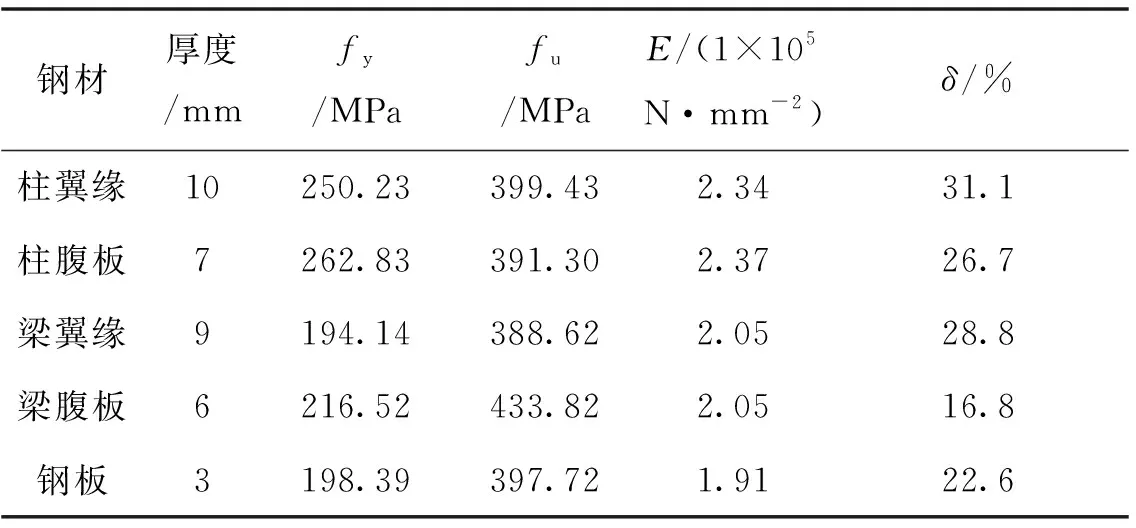
表1 钢材的材料性能Tab.1 Material properties of steel

1.2 加载方案

试验采用力和位移混合控制对试件顶部施加往复水平荷载，钢框架双钢板内填混凝土剪力墙试件屈服前采用力控制加载，每级荷载循环1次，试件屈服后采用位移控制加载，每级荷载循环3次.试件照片见图2(a)，试验加载装置如图2(b)所示.试件通过下部焊接的20 mm厚钢板与地梁连接，地梁固定在实验室的地面上.在剪力墙的平面外设置侧向支撑，阻止试件平面外变形.

图2 试验加载装置Fig.2 Test setup of specimen

1.3 测点布置

沿着试件的竖向布置D1-D4共4个位移计，分别布置在地梁处和1层、2层及顶部梁柱节点处.D-5和D-6为沿2层剪力墙对角线布置的位移计，用来测定剪力墙的剪切变形.A和B柱从下到上6个截面上分别布置应变片和应变花，观测钢柱在加载过程中的正应变和剪应变.在钢框架梁端部及中间3个截面的上下翼缘上布置应变片，腹板上布置应变花，观测钢梁的正应变和剪应变.为了观测钢板的剪应变，在剪力墙钢板表面沿对角线方向布置了应变花.位移计及应变片的布置位置如图3所示.

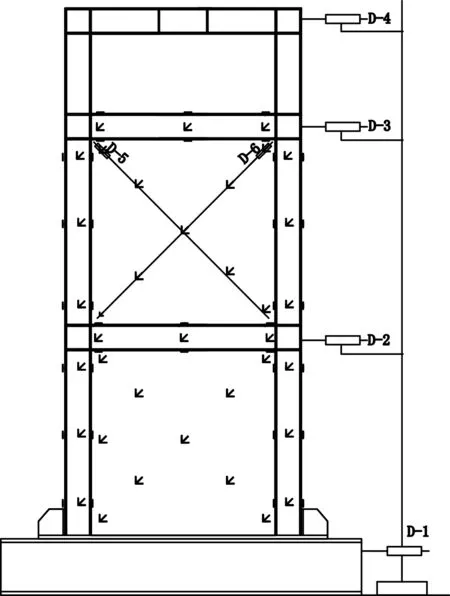
图3 测点布置图Fig.3 The sketch of measurement points

2 试验过程及现象

力加载阶段步长为30 kN，加载至±480 kN荷载级后，加载改为位移控制，位移加载步长取结构高度的0.2%，第一级位移加载为±27 mm。

加载至±30 mm荷载级，第1圈正向推到最大位移时，B柱柱脚处墙角钢板出现面外波状变形，变形呈45°方向，卸载后变形基本消失，反向拉时，墙板没有变化如图4(a)；加载至±42 mm荷载级，正向加载第1圈，B柱柱脚墙角出现第2道鼓曲，随着卸载，第2道变形恢复.反向加载第2圈，A柱柱脚墙角出现1道鼓曲，柱翼缘起皮；加载至±48 mm荷载级，剪力墙钢板出现面外波状变形，A、B柱翼缘都开始屈曲，卸载后变形恢复见图4(b)；加载至±54 mm荷载级，正向加载时，B柱翼缘屈曲，柱腹板面外波状变形，反向加载时，A柱翼缘屈曲，正向最大荷载为670.4 kN，负向最大荷载为-677.3 kN见图4(c).

图4 试验现象Fig.4 The experiment phenomena

加载至±60 mm，正向加载第1圈现象与54 mm相同，但屈曲程度加大，正向加载第2圈，加劲肋与柱脚焊缝被拉断[图4(d)]；加载至±66 mm荷载级，听到沙沙声，柱翼缘变形严重，柱腹板发生面外变形，墙角处钢板与柱之间的焊缝开裂，正向最大荷载为610.3 kN，负向最大荷载为-608.9 kN [图4(e)]；加载至±72 mm荷载级，正向加载第1圈，剪力墙钢板拉坏，正向加载第2圈，柱脚变形加剧，荷载下降到了峰值荷载的75%以下，试验结束[图4(f)].

试验过程中，剪力墙钢板未发生屈曲，说明内填混凝土可有效抑制钢板发生屈曲.钢板与梁柱之间采用角焊缝连接，试验过程中未发生破坏.钢框架双钢板内填混凝土剪力墙在水平荷载作用下，柱脚与地梁连接处的剪力墙墙角首先外鼓进入塑性，然后是柱脚底部翼缘屈曲进入塑性.本次试验的试件为两层半，试件高度较高，在水平荷载作用下，整个试件相当于悬臂构件，试件底部弯矩最大，试件破坏时表现为底部的钢柱翼缘局部屈曲，剪力墙下部鼓曲.在水平荷载作用下，仅为一层的剪力墙试件呈现的是剪切破坏，而当剪力墙高度较高时，整个剪力墙呈现的是弯剪破坏.实际工程中，钢框架双钢板内填混凝土剪力墙结构为高层结构，在地震作用下，容易发生压弯破坏.

3 试验结果分析

3.1 滞回曲线

钢框架内填混凝土双钢板剪力墙试件在往复荷载作用下的荷载与顶点及2、1层的位移滞回曲线如图5(a)-图5(c)所示.图中纵坐标表示施加在试件顶点的水平荷载，用符号F表示.横坐标表示梁柱节点处水平位移用符合Δ表示.图5(d)表示加载点荷载与2层层间位移曲线，横坐标表示的是2层的层间位移.在力加载阶段，试件处于弹性状态，表现为同一荷载级别下，试件的滞回曲线重合，卸载后残余变形小.随着荷载的增加，试件开始进入塑性，试件刚度下降，卸载后残余变形不断增加，试件耗散的能量越来越多.总体看来，钢框架双钢板内填混凝土剪力墙的滞回曲线比较饱满，滞回曲线基本呈梭形，说明试件耗能能力较强.达到峰值荷载后，试件承载力下降比较缓慢，说明试件后期刚度较大.

图5 试件滞回曲线Fig.5 Hysteretic loops of specimen

3.2 耗能能力

试件耗散能量的能力可由滞回曲线所包含的面积大小表达，一个滞回环所包围的面积即为所耗散的能量，滞回环包围的面积越大，耗散的能量越多.图6为试件1层、2层、顶点及2层层间在每级循环荷载作用下耗能曲线，随着荷载的增加，试件进入塑性的程度逐渐加深，滞回环包围的面积增大，结构耗散的能量逐渐增加.

图6 能量耗散Fig.6 Energy dissipation

等效粘滞阻尼系数也是检验试件耗能能力的指标，等效粘滞阻尼系数ξeq根据荷载位移滞回曲线所包围面积的包络线计算[15].图7为试件随着荷载增加，等效粘滞阻尼系数的变化曲线.随着试件进入塑性程度的加深，等效粘滞阻尼系数逐渐增大，钢框架双钢板内填混凝土剪力墙的耗能能力逐渐增强.

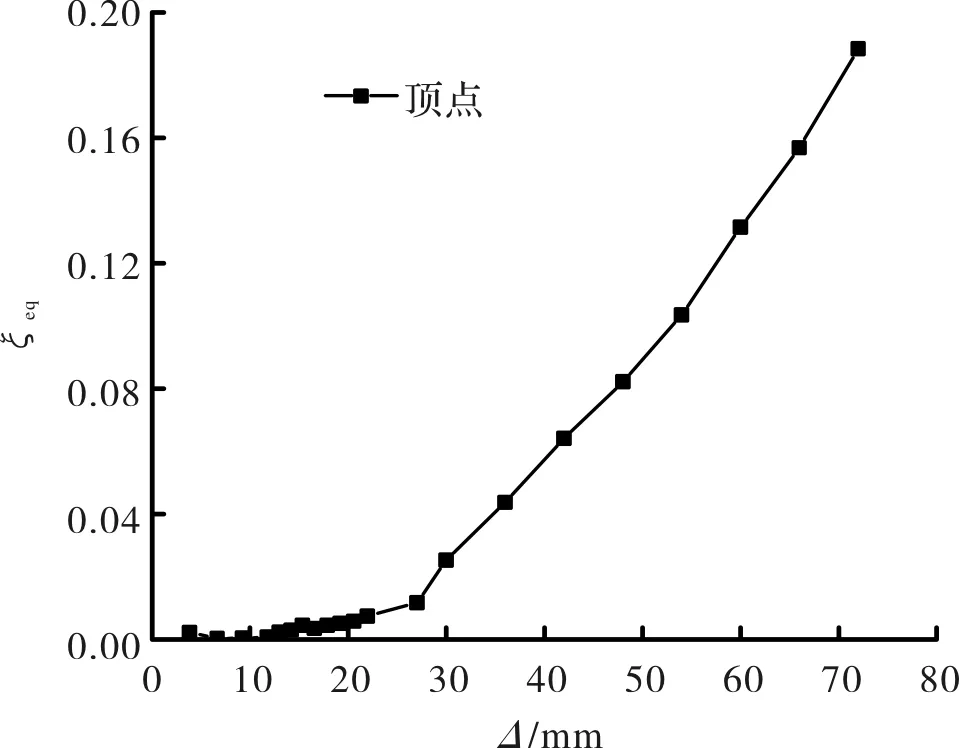
图7 等效粘滞阻尼系数Fig.7 Equivalent viscous damping ratio

3.3 试件的骨架曲线

试件的荷载位移骨架曲线如图8所示，由图中可见，试件顶部施加的水平荷载不大于±480 kN荷载级时，整个试件处于线弹性阶段，骨架曲线成一条直线，力和位移之间为线性变化.顶部施加的水平荷载超过±480 kN荷载级时，试件逐渐进入弹塑性状态，骨架曲线呈现弯曲趋势.试件达到了峰值荷载为-677.3 kN，此时顶点加载的水平位移为-54 mm。随后，试件的刚度下降，性能开始劣化.试件失效时，柱脚翼缘屈曲，底部剪力墙外鼓.由于钢框架双钢板内填混凝土剪力墙的1层与地梁之间为刚性连接，故而1层的抗侧刚度比2层略大.

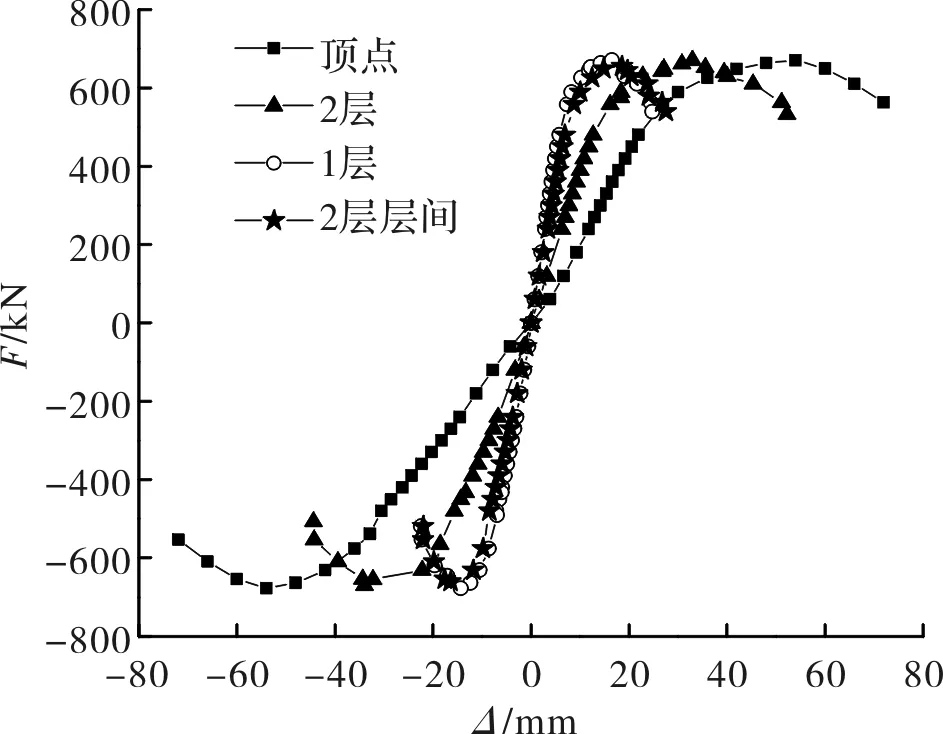
图8 骨架曲线Fig.8 Skeleton curves of specimen

3.4 主要阶段试验结果

钢框架双钢板内填混凝土剪力墙试件在试验主要阶段的荷载实测值、试件顶点位移及延性结果列于表2.表中H为试件总高度，Fy、Δy分别为屈服荷载、屈服位移，Fmax、Δm分别为峰值荷载、峰值位移，Fu、Δu分别为极限荷载、极限位移.μ为延性系数，是钢框架双钢板内填混凝土剪力墙试件极限位移与屈服位移的比值.

表2 主要阶段试验结果Tab.2 Experimental results at main stages

3.5 刚度退化曲线

图7为内填混凝土双钢板组合剪力墙试件刚度退化曲线，为了消除加载不对称的影响，侧向位移取同一滞回环正、负向顶点位移(Δ+、Δ—)绝对值之和的平均值，加载的荷载取同一滞回环正、负向顶点荷载(F+、F—)绝对值之和的平均值.计算时选取每级循环的第1周峰值荷载和对应的位移进行计算.采用割线刚度K来分析刚度退化，用式(1)计算[15].

(1)

图9 刚度退化曲线Fig.9 Curves of stiffness degradation

由图9可知，试件在试验过程中表现为平缓的刚度退化特征，试件整体和每一层刚度退化规律一致，随着荷载的增加，刚度逐渐平缓减小.整个试件的初始抗侧刚度为27.58 kN/mm，试件2层的初始抗侧刚度为38.58 kN/mm，试件1层的初始抗侧刚度为86.49 kN/mm，试件2层层间初始抗侧刚度为69.22 kN/mm。试件1层的层间初始抗侧刚度大.

3.6 承载力降低系数曲线

在同一级循环荷载作用下，随着循环荷载次数的增加，结构的承载能力会有所降低，结构承载力降低性能可用承载能力降低系数表示[15]，本文采用式(2)计算承载能力降低系数.

(2)

图10为试件承载能力降低系数曲线，由图中可见，加载初期，每一级循环荷载作用下，试件的承载力降低系数均接近于1.0，说明加载初期试件损伤较小.随着荷载的增加，试件损伤程度加深，同等位移幅值的条件下试件的承载能力有所降低，但降低程度很小，说明钢框架双钢板内填混凝土剪力墙的后期性能较好.

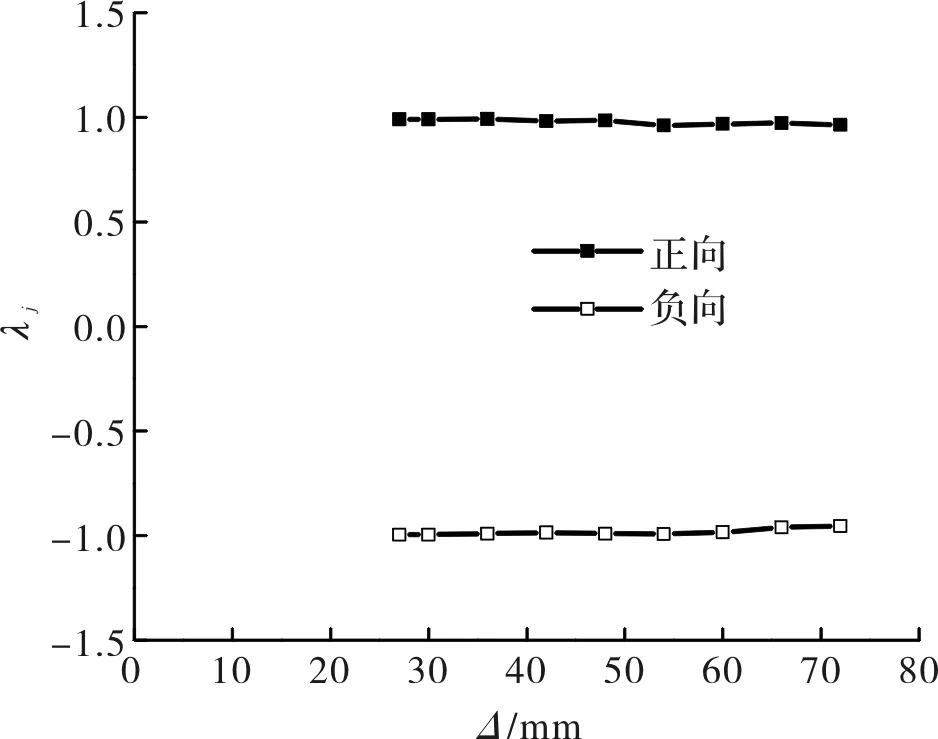
图10 承载力降低系数Fig.10 The load drop coefficient of specimen

3.7 剪力墙剪切变形

为了观测剪力墙的剪切变形，在试件的2层设置了沿对角线方向的位移计，用来测量对角线方向的伸长与缩短.图11—图12为剪力墙对角线伸长或缩短量与外加荷载之间的滞回曲线关系.图中F为施加的水平荷载，δ为位移计的伸长或缩短量.其中图12在施加正向荷载时，对角线缩短，图13在施加正向荷载时，对角线伸长.由图中可以看到，在弹性范围内，随着荷载的增加，对角线的伸长量和缩短量为线性变化.在达到极限荷载之前，剪力墙剪切变形比较小.加载后期，组合剪力墙的变形增加速度加快.在整个的加载过程中，二层剪力墙对角线的伸长量很小.图13为根据对角线变形计算得到的剪力墙剪切变形γ与施加荷载之间的滞回曲线，由图中可见，在整个加载的过程中，二层剪力墙的剪切变形很小.

图11 D-5位移计滞回曲线Fig.11 Hysteretic loops of D-5 displacement meter

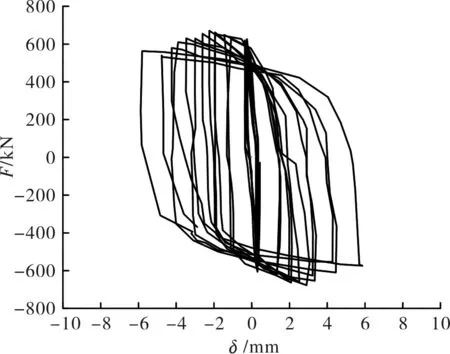
图12 D-6位移计滞回曲线Fig.12 Hysteretic loops of D-6 displacement meter

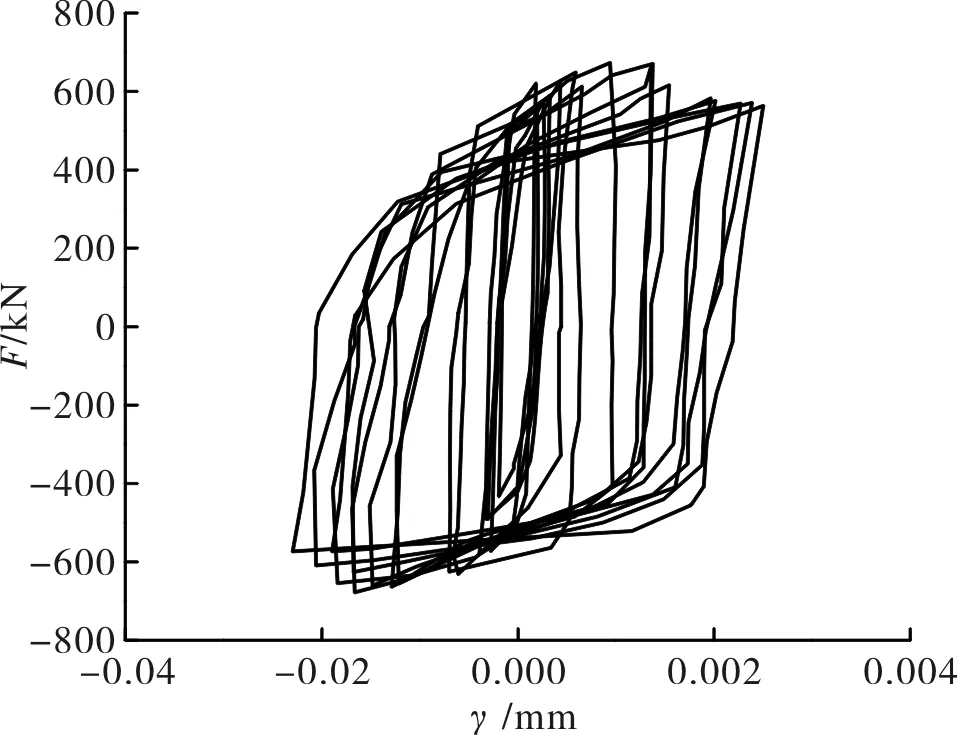
图13 剪切变形滞回曲线Fig.13 Shear deformation hysteretic loops

4 结论

(1)钢框架双钢板内填混凝土组合剪力墙水平承载能力高、抗侧刚度大、滞回曲线饱满，最终破坏模式为底部墙角外鼓，柱脚翼缘屈曲.

(2)与第2层相比，钢框架双钢板内填混凝土剪力墙试件1层层间刚度相对大，层间变形相对小，耗能相对少，剪力墙的剪切变形较小.

(3)钢框架双钢板内填混凝土剪力墙刚度退化平缓，试件整体和每一层刚度退化规律一致.

(4)钢框架双钢板内填混凝土剪力墙的承载能力降低系数接近1.0，同一加载级别下试件的承载力降低有限.