铅酸电池剩余放电时间预测方法研究

王 力

（甘肃中医药大学，甘肃 定西 743000）

0 引言

铅酸电池作为电源被广泛用于工业、军事和日常生活中。如何判定电池的剩余放电时间成为广大用户极为关注的问题。一般情况下，对铅酸蓄电池进行充放电，会对铅酸蓄电池的电荷量和寿命造成较大的影响，如果长时间的充电会导致正极板活性物质脱落现象的产生，降低使用的寿命。电池通过较长时间使用或放置，充满电后的荷电状态会发生衰减预测，需要解决以下的问题：

1）基于同一生产批次电池出厂时以不同电流强度放电测试的完整放电曲线的采样数据，进行综合分析，用初等函数表示各放电曲线，从而解决新电池使用中以不同电流强度放电时的剩余放电时间。

2）为了解决电池实际使用时的剩余放电时间，需建立20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型。

3）电池通过较长时间使用或放置，充满电后的荷电状态会发生衰减。分析得到从新电池到衰减状态1、衰减状态2、衰减状态3的放电时间依次递减，因此采用BP神经网络模型来预测衰减状态3的剩余放电时间。

1 模型假设及符号说明

1.1 模型的建立及求解过程中做出了以下假设

1）忽略电池自身结构因素（活性物质量及其组成、极板厚度以及孔率等）对模型的影响。

2）忽略放电电流密度差异对模型的影响。

3）忽略电解液密度对模型的影响。

4）终止电压相等，忽略了终止电压对模型的影响。

5）忽略外界环境因素（温度）对模型的影响。

6）假设在获取和处理数据时人为误差为零，对模型的影响可以忽略不计。

1.2 基本变量及符号说明

i：电流强度

U：电压

Um：额定最低电压

MRE：平均相对误差

T剩：剩余放电时间

2 铅酸电池放电曲线分析

2.1 放电曲线

通过分析同一生产批次电池出厂时以不同电流强度放电测试的完整放电曲线的采样数据，发现电流强度分别 在 20A、30A、40A、50A、60A、70A、80A、90A和100A时随着放电时间的增加电压均表现为下降趋势，可以说明电池在九种电流强度下的放电趋势一致。因此选择spss18.0软件对放电时间和九种电流强度下的电压分别进行了回归分析，分析表明二项式关系的回归系数最高，所以最终选择以二项式来模拟电压与放电时间的动态变化，即电池在九种电流强度下的放电曲线。通过回归分析之后对九种电流强度下的放电曲线进行二项式模拟，结果见图1和表1，可以看出R2均在0.960以上，说明通过模拟出来的二项式能够预测一定电流强度下的放电趋势。

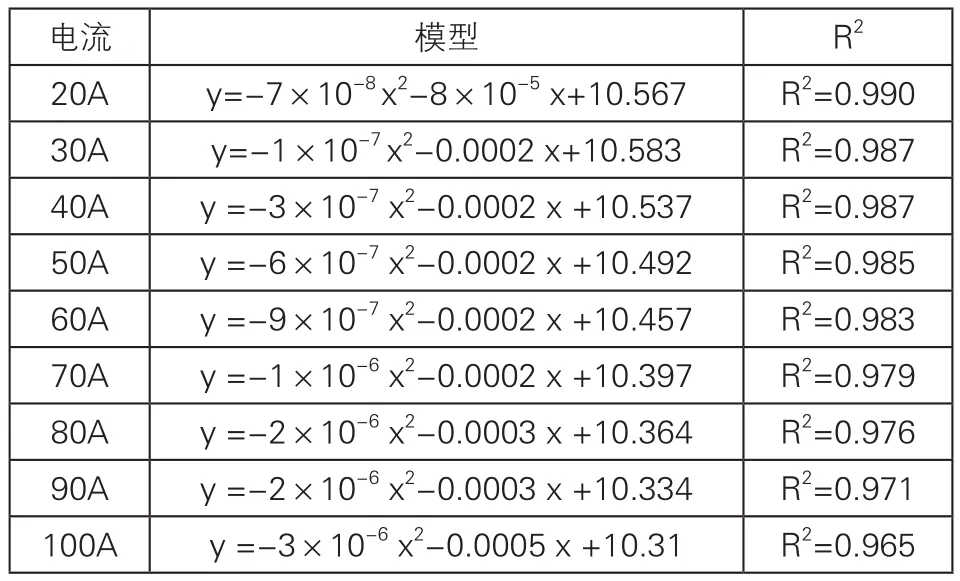
表1 电池在不同电流强度下的放电时间曲线模型

图1 电池在不同电流强度下的放电时间曲线模型

2.2 平均相对误差MRE

基于等时间间隔采样在低电压段的采样点相对稀疏的事实，提取231个U值差值不超过0.005V的U值，利用模拟出来的二项式模型算出模拟电压值，得出平均相对误差MRE值，从表2中可以看出平均相对误差值在8.05-14.61%之间，表明利用二项式模拟出来的模型精确度较好，更进一步说明该模型能够精确的预测一定电流强度下的放电剩余时间。

2.3 剩余放电时间的计算

在新电池使用中，当电压一定时根据模拟出来的放电曲线推断出放电时间，剩余放电时间为特定电压时的放电时间减去终止电压时的放电时间。测得电压均为9.8V，额定最低电压为9.0V，所以剩余放电时间T剩=T9.0-T9.8。利用模型分别算出U=9.8V的放电时间和Um=9.0V的放电时间，二者相减即为电池在该电流强度下的剩余放电时间，结果为表3所示。

表2 二项式模型所得预测值与实际值的平均相对误差

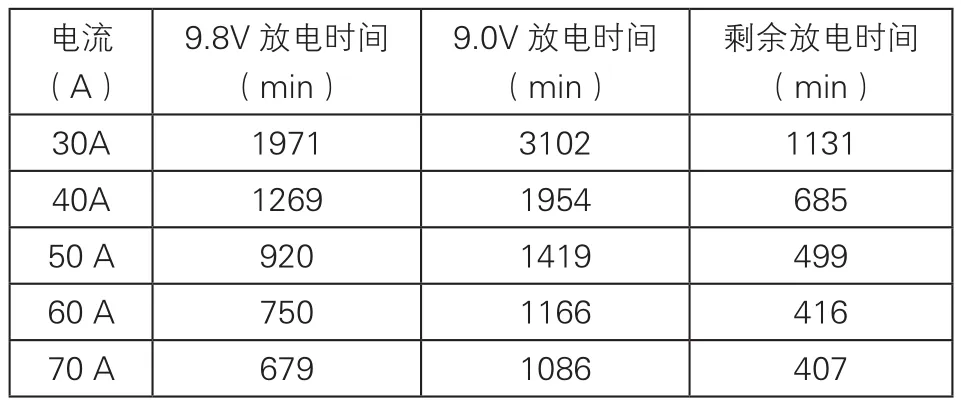
表3 电流强度在30A、40A、50A、60A和70A的剩余放电时间表

为了解决电池实际使用时的剩余放电时间，需建立20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型。从电池在20-100A九种电流强度下的放电曲线可以得出任一恒定电流强度放电时的曲线同样为二项式模型，所以根据已经模拟出来的二项式（表1）各系数与电流建立关系式，从而获得任一恒定电流强度的放电曲线。定义为y=ax2+bx+c。

具体先提取模拟出来的20-100A九种不同电流强度的二项式放电曲线的各项系数，通过分析各项系数得出关于电流的一条曲线和函数，获得对应的函数即为任一恒定电流强度下的放电曲线的各系数，由此可以确定以20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型。

二次项系数确定：经回归分析检验得出20-100A九种电流强度下的放电曲线二次项系数表现为二次关系最好，所以建立二次方程为:

a=-4×10-10i2+1×10-8i-2×10-7。

一次项系数确定：由于九种电流强度下的放电曲线的一次项相差不大，所以选用算术平均值来决定一次项系数，求得算术平均值为-0.00024即b=-0.00024

常数项确定：不同电流强度下的放电曲线常数项呈现线性相关关系，建立线性方程为c=-0.0037i+10.67。

以任一恒定电流强度放电时的放电曲线模型为：y=（-4×10-10i2+1×10-8×i-2×10-7）x2-0.00024x+（-0.0037×i+10.67）。

将20-100A九种电流强度带入模拟出来的放电曲线模型，得出特定电流强度下的放电曲线，用新获得的放电曲线计算出不同放电时间下的电压，随机选取同一时间下的231个Um差值不超过0.005V的Um值，算出实际值与预测值的平均相对误差RSE=10.58%，平均相对误差较小，且从图2中可以看出预测和实际电压值相差也不大，说明用这种方法模拟出来的模型能够作为任一恒定电流强度放电时的放电曲线。

图2 任一恒定电流模型所得预测值与实际值比较图

2.4 电流强度为55A的放电曲线

前面建立了任一恒定电流强度放电时的放电曲线模型为：y=（-4×10-10i2+1×10-8×i-2×10-7）x2-0.00024x+（-0.0037×i+10.67）。各项系数为电流强度的函数，当电流强度为55A时各项系数为常数，具体为

a=-4×10-10i2+1×10-8×i-2×10-7=-9×10-7

b=-0.00024

c=-0.0037×i+10.67=10.467

所以当电流强度为55A时的放电曲线为表4和图3所示。

表4 电流强度为55A时的放电曲线表

图3 电流强度为55A时的放电曲线图

3 预预测电池衰减状态及剩余放电时间

3.1 预测电池的衰减

电池通过较长时间使用或放置，充满电后的荷电状态会发生衰减。通过对同一电池在不同衰减状态下以同一电流强度从充满电开始放电的记录数据的分析，新电池的放电时间明显比较长，根据时间序列推断衰减状态1、衰减状态2、衰减状态3的使用或放置时间依次递减，因此采用BP神经网络模型来预测衰减状态3的剩余放电时间。

BP网络（Back-ProPagation Network）又称反向传播神经网络，通过样本数据的训练，不断修正网络权值和阈值使误差函数沿负梯度方向下降，逼近期望输出。它是一种应用较为广泛的神经网络模型，多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。 BP网络由输入层、隐层和输出层组成，隐层可以有一层或多层，BP网络模型，网络选用S型传递函数，通过反传误差函数（Ti为期望输出、Oi为网络的计算输出），不断调节网络权值和阈值使误差函数达到极小。

3.2 数据处理

我们采取数据前148组作为输入，即电压，新电池状态，衰减状态1，衰减状态2，将对应的衰减状态3作为输出。并用matlab自带的premnmx（ ）函数将这些数据归一化处理。

数据集：见表5（注意：每一列是一组输入训练集，行数代表输入层神经元个数，列数输入训练集组数）。

表5 不同衰减状态的电压

该模型由每组数据的电压、新电池状态、衰减状态1、衰减状态2指标作为输入，以衰减状态3作为输出。

BP神经网络通常采用Sigmoid可微函数和线性函数作为网络的激励函数。本题选择S型正切函数tansig作为隐层神经元的激励函数。而由于网络的输出归一到[-1，1]范围内，因此预测模型选取S 型对数函数tansig作为输出层神经元的激励函数。

此次预测可以选用matlab中的神经网络工具箱进行网络的训练。将训练样本数据归一化后输入网络，设定网络隐层和输出层激励函数分别为tansig和logsig函数，网络训练函数为traingdx，网络性能函数为mse。设定网络参数，网络迭代次数epochs为50000次，期望误差goal为0.00000001，学习速率lr为0.0001。设定完参数后，开始训练网络。网络训练完成后，只需要将各项素质指标输入网络即可得到预测数据。

通过上述分析和建立的电池衰减及剩余放电时间模型，说明放电时间与电压、电流以及电池的衰减有着密切的关系，在实际应用中必须考虑放电时间及其电池的使用状态和环境，同时也要考虑导致电池衰减状态与剩余放电时间的其他因素。