波动方程 给力高考

湖北 朱木清

物理《选修3 - 4》，例析弹簧振子和单摆模型，介绍了简谐运动规律表达式(也叫振动方程)。结合绳波和弹簧波模型，讲解了机械波的形成机理与过程：沿着波的传播方向，介质中相邻质点间相互作用，前面的质点依次带动后面的质点振动，后一质点总是重复前一质点的振动状态，“滞后”一定的时间和相位。

一、平面简谐波的波动方程

设Ox轴上有一平面简谐波传播，波速为v，已知其中某质点(可能是波源，也可能不是，称为始点)偏离平衡位置的位移y0与时间t关系为

y0=Acosωt

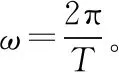
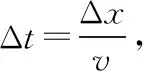
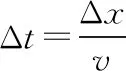
二、波动方程在高考中的应用

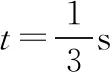
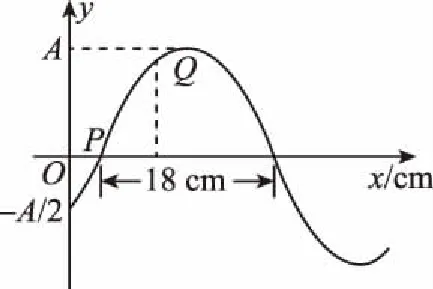
(ⅰ)波速及波的传播方向；

(ⅱ)质点Q的平衡位置的x坐标。

甲

乙

【解析】(ⅰ)由图1甲知波长λ=36 cm

由图1乙知周期T=2 s

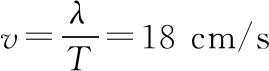
(ⅱ)P、Q平衡位置间距离不是特殊值，故适用波动方程求解。由图1乙，设质点Q的偏离平衡位置的位移与时间关系式为yQ=Asinωt

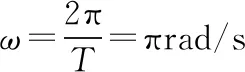
故yQ=Asinπt

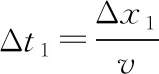
偏离平衡位置的位移与时间的关系式分别为

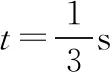
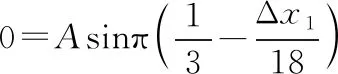
故质点Q的平衡位置的x坐标xQ=9 cm。

【拓展】如表1，仿照对质点Q的描述，完成质点O和P的对应分析。

表1

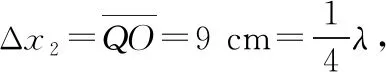
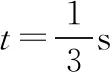
表2

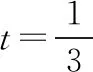
(ⅰ)简谐波的周期、波速和波长；

(ⅱ)质点O的位移随时间变化的关系式。

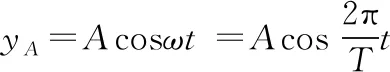
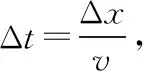
t=1 s时，质点A第一次回到平衡位置

得周期T=4 s

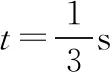
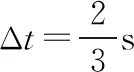
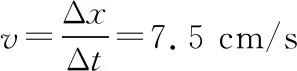
波长λ=vT=30 cm

t=0时刻波形图如图3所示。

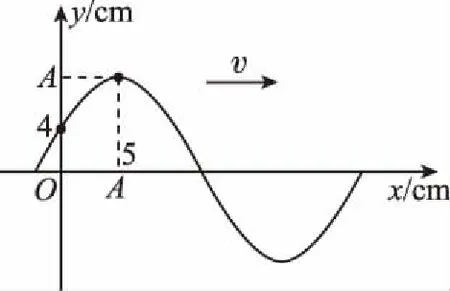
图3

(ⅱ)t=0时，质点O位于y=4 cm处

得振幅A=8 cm

故质点O的位移随时间变化关系式为

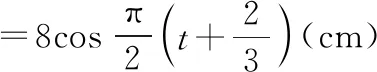
解法二：(ⅰ)t=0时，质点A位于波峰位置

t=1 s时，A处质点第一次回到平衡位置

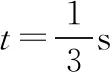
t=1 s时，A第一次到平衡位置

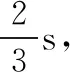
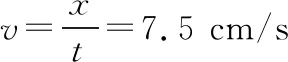
波长λ=vT=30 cm。

(ⅱ)设质点O的振动方程为

y=Asin(ωt+φ0)

又t=0时，质点O的位移为y=4 cm，4=Asin(0+φ0)

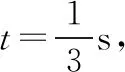
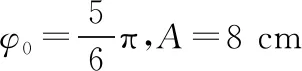
得质点O的位移随时间变化关系式