18月龄回交鲷生长性状的相关分析与通径分析
刘海林, 祝 斐,2, 张志勇,2, 许 津, 贾超峰,2, 孟 乾,2, 张志伟,2,陈淑吟,2, 张曹进, 吴国均, 任忠宏, 陈宏兵
(1.江苏省海洋水产研究所,江苏南通 226007; 2.江苏省海水鱼类遗传育种重点实验室,江苏南通 226007)
鲷科(Sparidae)隶属硬骨鱼纲(Osteichthyes)鲈形目(Perciformes)鲈亚目(Percoidei),据统计,世界鲷科鱼类共34属133种,而我国鲷科鱼类现有7属18种[1],鲷科资源主要以黑鲷与真鲷为主。真鲷(Pagrusmajor)适温范围为20~28 ℃,真鲷适盐范围为17‰~31‰,最适水温为26~28 ℃,最适盐度为25‰~30‰[2-3],是我国沿海网箱养殖量最大的鲷科鱼类,生长速度较黑鲷快,易起捕但肉质粗糙,经济价值较差。黑鲷(Acanthopagrusschlegeli)适盐范围为8‰~32‰,最适盐度为25‰~28‰,适温范围为8~30 ℃[4],抗逆性强。近些年来,随着海水鱼养殖业的迅速发展,海水养殖品种趋于单一,鲷科鱼类养殖近亲繁殖严重[5],导致鲷科鱼类病害发生率增高[6],种质退化明显。因此,迫切须要培育出具有较高经济性状的鲷科鱼类新品种。国内外科研工作者很早就开始了有关杂交鲷科鱼类的研究[7],其中江苏省海洋水产研究所通过潜心育种研究,不断优化杂交组合,首次培育出具有育种潜力的回交鲷F1代等杂交组合,但未见关于回交鲷形态性状与体质量指标的相关报道。众所周知,体质量等经济性状是选育优良品种的目标性状,多代的性状选择和淘汰在选育工作中十分重要。考虑到在实际生产中逐一测定体质量的操作难度较大,相比而言可视化的性状如全长、体高、头长等是比较直观的性状,如果能够依据表观形态性状测定,采用多元回归分析的方法分析体质量与全长、体高、头长等形态性状之间的关系,从而指导选择育种工作,则具有现实意义。
多元统计方法计算通径分析(path coefficient analysis)最早被遗传学家Sewall Wright于1921年提出,用以揭示自变量和因变量的直接相关性大小和研究自变量对因变量的直接和间接影响[8]。随着多代水产数量遗传学家不断完善改进,该方法已被广泛应用于水产育种研究中[1,9-14]。鲷科中仅有Kora等利用多元相关分析真鲷体长、体质量与脂肪含量的相关性,尚未见有关黑鲷和杂交鲷形态性状和体质量相关关系的报道[15]。本研究通过回归方程中的形态性状对体质量的回归分析,为鲷科鱼类的良种形态性状的选育提供基础资料。因此,对回交子代和黑鲷子代的主要外部形态框架研究对鲷科良种选育具有十分重要的意义。
1 材料与方法
1.1 样本来源
1.2 样品测量
各长度性状的指标参考如图1所示刘贤德等的方法[12]进行测定。框架数据利用相机拍照校准后,用Digimizer数字图像法[15-18]测量全长(AL)、体长(BL)、头长(HL)、躯干长(TL)、尾柄长(PL)、吻长(SL)、眼径(ED)、尾鳍长(FL)、体高(BD)、尾柄高(PH),用电子天平称体质量(精度达到1 g)。

1.3 数据处理
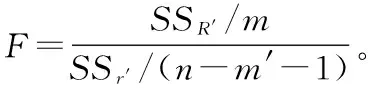
2 结果与分析
2.1 各形态性状统计结果和正态性检验
30尾回交鲷F1代的体质量、全长、体高等表型数据经整理后见表1。在这些性状中,回交鲷F1代均以体质量变异系数最大,全长、体长、体高和尾柄高的变异系数均较小。
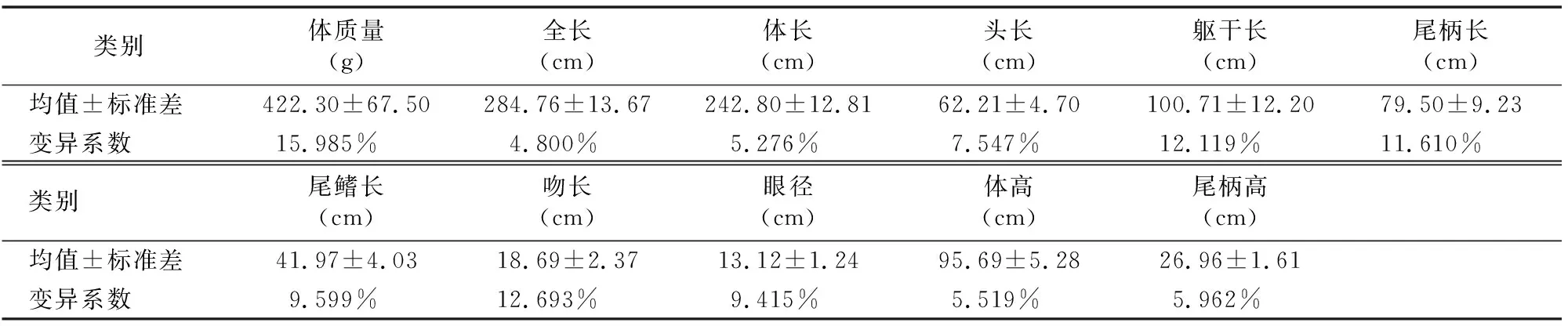
表1 回交鲷11个性状的统计结果
注:样本数为30尾。
2.2 性状间的相关系数
回交鲷F1代各性状及体质量相互间的表型相关系数见表2。回交鲷F1代所列各性状间的表型相关性部分为显著或极显著水平。回交鲷各形态性状与体质量相关关系大小顺序为体高>体长>全长>尾柄长>躯干长>尾柄高>头长>吻长>眼径>尾鳍长。相关系数分析测定的只是2个性状之间的密切程度,在多个性状间存在相关性时,这种相关性只能反映其复合关系,并不能表明各个性状与体质量作用的原因和效应的程度。为进一步确认各性状对提高体质量的重要性,须要运用通径分析的方法进行研究,采用逐步多元回归建立体质量与形态性状的回归方程。
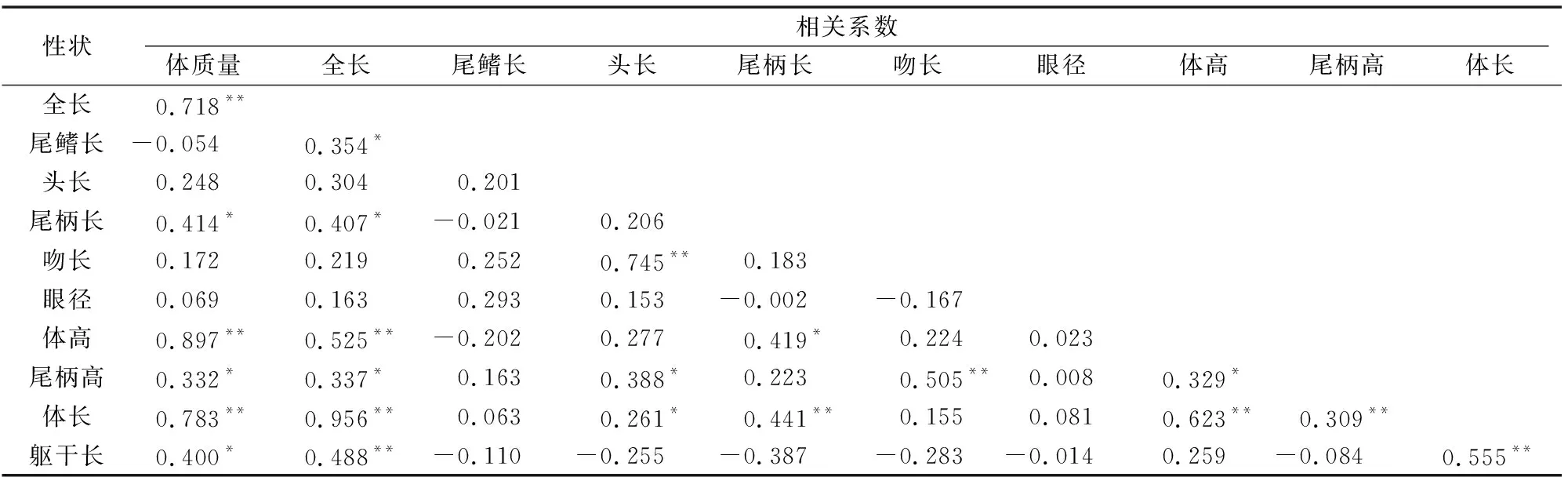
表2 黑鲷和回交鲷各形态性状间的相关系数
注:“**”“*”分别表示在0.01、0.05水平上差异显著。
2.3 各性状对体质量影响的通径系数和作用分析
对因变量Y(体质量)进行正态性检验,因本研究中各组样本量n=30,属于小样本,所以利用Shapiro-Wilk检验,回交鲷Shapiro-Wilk Test统计量=0.954,P=0.214>0.05,所以2组的体质量服从正态分布,即Y是正态变量,可以进行下一步回归分析。
本研究在相关分析的基础上,以回交鲷的体质量为因变量(Y)、外部形态性状为自变量(X1~X10),采用逐步法进行多元线性回归分析。经多元线性回归显著性检验,2组体长的共线性统计量(variance inflation factor,简称VIF)均大于10,存在较强的共线性,须排除[21]。显著性检验结果表明,2组鱼的自变量(体高和全长)和因变量(体质量)之间均存在显著性差异(P≤0.01),具有统计学意义,在方程中保留。各自变量的偏回归系数、方程截距、通径系数(标准回归系数)、标准误差以及相对应的显著性检验结果见表3和表4,根据表3选择偏回归系数显著的变量,与体质量建立多元回归方程如下:
Y=-935.502+9.173BD+1.686TL。
通径系数是标准化的偏回归系数,因此对偏回归系数进行显著性检验与通径系数检验的效果是等价的。
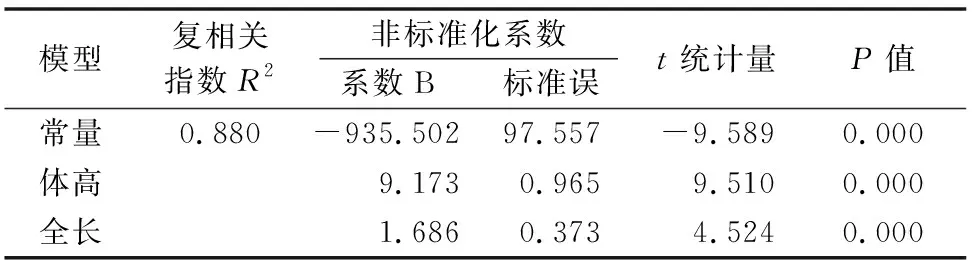
表3 回交鲷偏回归系数和回归常数
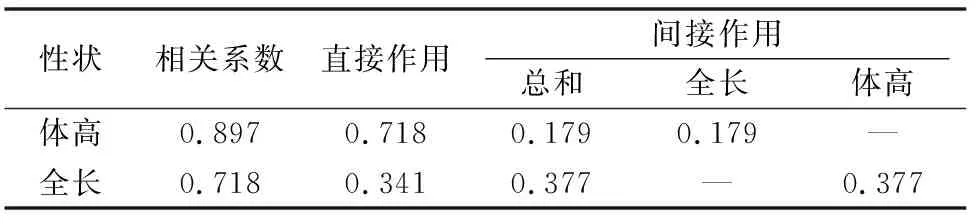
表4 回交鲷形态性状对体质量的通径系数
3 结论与讨论
3.1 自变量与因变量的相关关系
表型相关分析只是简单地估测了2个变量之间的相关系数,而相关系数分成2个变量间的直接作用和通过其他有关变量的间接作用两部分。直接作用部分即通径系数,它不受其他变量的影响而是自变量与因变量之间的真实关系。自变量与因变量的相关系数达到极显著水平,但通径系数检验并不显著[22]。这是因为两者的直接关系和通过其他变量的间接关系的正负作用相互抵消的结果[23]。例如在本研究中发现,回交鲷的尾柄高和躯干长对体质量的影响达到正向显著水平(P<0.05),但通径系数却不显著(P>0.05),说明尾柄高和躯干长对体质量的直接影响较小,其影响主要是通过其他性状如体高和全长作用。
3.2 影响回交鲷体质量的重点性状的确定
对回交鲷测量性状的通径系数进行显著性检验,剔除共线性强的体长性状,结果表明,回交鲷的体质量均与体高和全长有极显著关系(P<0.01),体高对体质量的决定系数最大,为0.718。在多元线性回归分析中,R2表示利用回归方程进行预测的可靠程度,只有当R2大于或等于0.85时,表明影响依变量的主要自变量已经找到[13,24]。在本研究中,通过保留通径系数显著的变量建立性状对体质量的回归方程,回交鲷复相关指数0.880大于0.850,表明保留的性状对体质量的影响为主要自变量,其他未测定或是被剔除的性状对体质量的影响相对较小。通过对回交鲷群体形态性状与体质量进行通径分析发现,影响体质量的主要性状为体高和全长,而影响回交鲷体质量的主要性状强弱程度依次为体高、全长,因此在进行回交鲷良种选育时,应以体高、全长为基础建立相应的选育测量指标。
3.3 回交鲷数量性状的选育
多元回归分析方法在其他水产动物中已被广泛应用[25-28],但在回交鲷性能选育中的研究尚未见报道。数量性状的生长指标一般可分为长度测量及体质量测量2种[29]。在本研究中,主要以回交鲷形态性状的相关关系以及对体质量的作用大小作为判别标准,初步确定了影响体质量的主要形态性状,发现影响体质量的形态性状集中在鱼体的长度和高度方面,建立了以形态性状为自变量、体质量为依变量的回归方程,并尝试用方程拟合手段拟合。因此,在回交鲷的良种选育中,以体质量作为主要选育性状,将全长、体高等性状作为辅助性状,采用多性状选择指数法,把形态性状纳入选择指数中,将有效地提高良种选育效果。
——与非适应性回归分析的比较

