施肥量和施肥比例对小麦生长的影响研究——基于多元方差分析算法和最小二乘法

张政谦

（河南大学软件学院，河南 开封 475004）

1 问题分析

施肥量和施肥比例的变化都会不同程度地影响小麦所含各种糖分的变化，因分析发现糖分种类之间关联性强，用因子分析降维减少复杂度，再对降维后的数据进行两因素（施肥量和施肥比例）、三水平（低氮，中氮，高氮；0∶4，1∶3，2∶2）的方差分析得到因素的显著性影响，得到小麦含糖量最高时对应的施肥量和施肥比例。

2 模型的建立与求解

糖的种类较多，希望用较少的新变量代替原来较多的变量，同时要求这些新变量尽可能反映原变量的信息，因子分析正是解决这类问题的有效方法，简化降维，从而使问题更加简单、直观。

因子分析是通过对变量之间关系的研究，找出能综合原始变量的少数几个因子，使得少数因子能够反映原始变量的绝大部分信息，然后根据相关性的大小将原始变量分组，使得组内的变量之间相关性较高，而不同组的变量之间相关性较低。因此，因子分析属于多元统计中处理降维的一种统计方法，其目的就是减少变量的个数，用少数因子代表多个原始变量。

2.1 建立模型

原始的p个变量表达为k个因子的线性组合变量，设p个原始变量为x1，x2，……，x6，寻找的k个因子（k＜p）为f1，f2，……，fk，成分和原始变量之间的关系表示为：

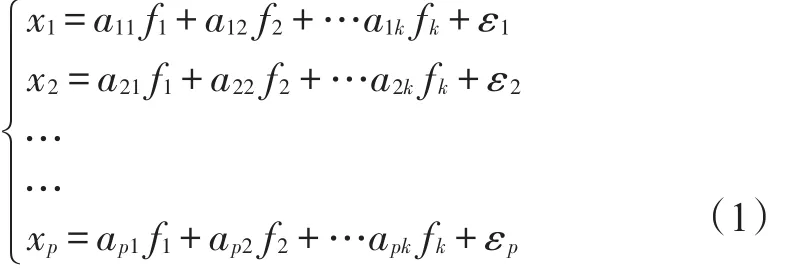
2.2 数据检验

计算各变量之间的相关矩阵，观察各相关系数，如表1所示。各变量之间相关系数的绝对值大都接近于1，故适合因子分析。

表1 各变量的相关系数

2.2.1 因子提取。从图1碎石图可以得到，纤维素在所有在所有糖成分中特征值占比最大，可作为主成分因子。然后利用主成分分析（抽取了一个成分）提取因子，如表2所示。

2.2.2 因子命名。定义因变量为含糖量，用以表示各种成分，利用SPSS得出系数矩阵见表3。

降维后得到的含糖量表达式：

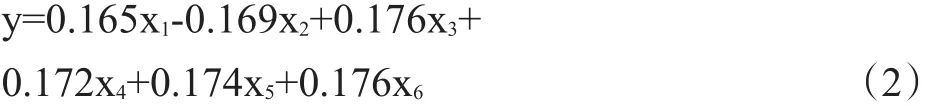
式（2）中，x1，x2，……，x6分别代表纤维素、淀粉、蔗糖、果糖、还原糖和总糖。

2.2.3 方差检验。方差分析的基本原理是认为不同处理组的均数间的差别基本来源有2个。一是实验条件，即不同的处理造成的差异，称为组间差异。用变量在各组的均值与总均值之偏差平方和的总和表示，记作SSB，组间自由度DFB。二是随机误差，如测量误差造成的差异或个体间的差异，称为组内差异，用变量在各组的均值与该组内变量值之偏差平方和的总和表示，记作SSW，组内自由度DFW。总偏差平方和SST=SSB+SSW。

之后构建F分布：

将F值与其临界值进行比较，在调用做方差分析之前，应先检验样本数据是否满足方差分析的基本假定，即检验正态性和方差齐次性。首先，正态性。调用jbtest函数检验含糖量是否服从正态分布，原假设是含糖量服从正态分布，备择假设是不服从正态分布，由结果h=0可知服从正态分布。其次，方差齐次性。由假设可知：经过正态性检验和方差齐次性检验之后，利用析因设计方差分析去检验每个因素的水平效应均值的统计差异，也能检验因素间的交互影响。基本原理仍为离差平方和的分解。

图1 因子碎石图

表2 各个糖的因子成分

表3 糖的系数矩阵

表4 方差分析结果

总变异=施肥量的各个水平间的差异+施肥比例因素各水平间的差异+施肥量与施肥比例的各种不同水平组合之间的差异+观察数据的随机误差及组内差异。

建立数学模型为：

式（4）中，μ为平均数；ai为Ai的效应；bj为Bj的效应；（ab）ij为Ai与Bj的互作效应，（ab）ij=（μij-μ）-（μi-μ）-（μj-μ）=μij-μi-μj+μ，μi、μj、μij分别为Ai、Bj、AiBj观测值总体平均数。

离差平方和与自由度分解：SST=SSA+SSB+SSAB+SSe；dfT=dfA+dfB+dfAB+dfe。其中，SSAB、dfAB为因素A与因素B交互作用平方和与自由度。

总平方和与自由度：

因素水平组合平方和自由度：

A因素平方和与自由度

B因素平方和与自由度

所以，相应均方为：MSA=SSA/dfA，因素A的方差；MSB=SSB/dfB，因素B的方差；MSAXB=SSAXB/dfAXB，A、B互作的方；MSe=SSe/dfe，误差方差。

通过上述表达式计算得到方差分析表，见表4。当P值小于0.05时，接受原假设，反之，拒绝原假设。

根据SPSS的数据分析可知：①施肥量对小麦含糖量影响显著；②施肥比例对小麦含糖量有一定影响，但影响不显著；③施肥量和施肥比例的相互作用对小麦含糖量无显著影响。

3 模型检验

画出估算边际均值图见图2。从图2含糖量的估算边际均值可以看出低氮情况下含糖量最大，影响最为显著，施肥比例虽有影响，但没有那么明显，与所得到的结果一致，要想得到更多的含糖量，应选用低氮0∶4的施肥方式。

图2 含糖量的估算边际均值

但对于各种不同的糖分来说，由于淀粉是负相关的，低氮情况下，淀粉含量反而越低。这与淀粉自身聚合物属性也保持一致，淀粉是植物体内的储能物质，淀粉水解会产生还原性二糖麦芽糖、单糖葡萄糖，进而增加植物的糖含量。