一种基于有限时间稳定的环绕控制器设计
张春燕 戚国庆 李银伢 盛安冬
在无人机对目标跟踪任务中,目标主要分为合作目标和非合作目标.对合作目标跟踪,无人机如何在速度受限条件下实现在传感器适用范围内环绕目标运动是目标跟踪的研究重点之一;对非合作目标,无人机必须保持在目标一定距离外跟踪以减少暴露风险.这些应用需求导致了近年来环航跟踪方法的快速发展.
环航跟踪指无人机保持一定距离环绕跟踪目标,即控制器需要实现无人机在以目标为圆心、指定距离为半径的期望航迹上航行.当前对无人机环航的研究主要包括观测器和控制器的设计.一些学者采取观测器与控制器相耦合的策略.针对单传感器跟踪单目标,Deghat等[1]提出纯方位量测下的目标环绕跟踪的观测器和控制器的设计方法,并针对观测器为非完整机器人时进行改进[2],随后扩展到单传感器对多目标的环航跟踪中[3];与纯方位量测对应,Shames等[4]提出在单传感器纯距离量测下的环航跟踪观测器和控制器;Cao[5]等基于距离和距离变化率提出一种环航跟踪控制器,在此基础上,张民等[6]提出结构更简洁的控制器,并扩展到运动目标的跟踪中;Matveev等[7]基于距离和距离变化率信息,针对单传感器对多目标环航跟踪提出一种控制器的设计方法;Zhang等[8]针对单传感器跟踪单目标提出一种基于视觉的观测器,并分析在存在目标丢失情况下的稳定性;Zhu等[9]提出一种改进的自适应算法估计目标速度,并利用Lyapunov向量场保证控制器的收敛性.
另一些学者主要研究控制器设计,前提是已由其他探测设备得到目标的运动状态.Lawrence[10]针对无人机环航跟踪问题,提出基于Lyapunov向量场引导法(Lyapunov vector field guidance,LVFG)的环航控制器;Frew等[11]和Summers等[12]针对无人机速度受限提出一种解耦控制结构;Yoon等[13]利用Backstepping使无人机在速度受限的情况下完成空间环航跟踪;Wang等[14]提出一种基于弹性引力和斥力的控制方法;Oh等[15]为进一步分析目标速度对环航跟踪的影响,利用微分几何的方法明确指出绕飞中无人机速度与目标运动状态的关系;Shames等[16]考虑了无人机环航跟踪时的避障问题;为使无人机更快速地收敛,Chen等[17]提出一种基于切向量场引导法(Tangent vector field guidance,TVFG)的控制方法,但当无人机在期望距离内时控制方案依然为Lyapunov向量场引导法.多种现代控制策略被应用到环航跟踪研究上,例如模型预测控制[18−19]、自适应滑模控制[20]、动态规划[21]、路径规划[22]、分布式控制[23]等.另外,Zhu等针对环航跟踪中无人机输入受限的问题提出Bang-Bang控制[24]和饱和控制策略[25].
上述成果提出多种可行的环航控制方案,给出在这些控制器下无人机对目标环航跟踪进一步的研究成果,但对上述控制器之间的优缺点对比给出的结论较少.另外,关于无人机收敛到期望航迹的问题,人们总是更希望无人机能在有限时间内到达期望航迹,有限时间稳定控制器可以保证闭环系统状态在有限时间内收敛到平衡点[26−31],但工程应用中,无人机速度普遍会受到限制,如何保证无人机在此情况下更快速地收敛是需要研究的课题.
本文针对工程应用中目标速度变化情况,根据无人机和目标的几何关系,提出一种考虑目标运动状态的控制方案,给出一类基于该控制策略可行的控制参数条件.通过比较这类控制器的优缺点,提出一种具有快速收敛性、更好抗扰动性的有限时间饱和控制参数条件.
本文结构安排如下:第1节描述研究的问题;第2节给出有限时间控制器的设计方案;第3节给出仿真比较结果;第4节是结论.
本文中,R表示实数集,R+表示正实数集,为欧氏范数,sgn(·)表示符号函数(sgn(0)=0),AB表示集合{x|x∈A,x/∈B}.
1 问题描述
如图1所示,本文主要考虑固定翼无人机对目标的环航跟踪问题.例如文献[8],假定无人机配有一个低空飞行控制系统,可接收到速率、角速度指令转化为相应的横滚、俯仰和偏航信息,同时具有速度保持和定高飞行功能.因此,无人机主要针对地面、水面或同一水平面的目标进行环航跟踪,即只考虑无人机与目标在X-Y平面下的相对运动状态.假设已经由其他探测设备得到目标的速度信息,本文主要研究无人机对目标环航跟踪的飞行控制器设计.基于工程应用与控制实现要求,假定无人机的速度受限,且满足无人机速率大于目标速率.

图1 系统模型Fig.1 Model of the system
1.1 飞行环绕问题描述和系统模型
由于将无人机视为质点,以无人机速度为输入设计控制器,因此在笛卡尔二维坐标系下,设无人机的运动模型为[5]


其中,vmin,vmax分别表示无人机的最大和最小航行速率.
目标的位置和速度由其他探测设备实时探测得到,因此考虑到目标在笛卡尔二维坐标系下的运动模型为

根据环航跟踪的控制要求,对无人机和目标的相对运动和位置建模.在同一笛卡尔坐标系下,定义无人机与目标的相对速度为νr,则

即相对运动模型为

其中,变量[xryr]T∈R2表示无人机相对于目标的位置.如图1所示在极坐标下系统模型(5)的输出表示为

其中,d∈R+表示无人机与目标之间的相对距离,θ∈[0,2π)表示无人机与目标之间的方向角.控制器设计要求距离收敛到期望值,可以表示为

其中,d0∈R+表示无人机和目标的期望距离.
由要求目标速率小于无人机的最大速率得出:
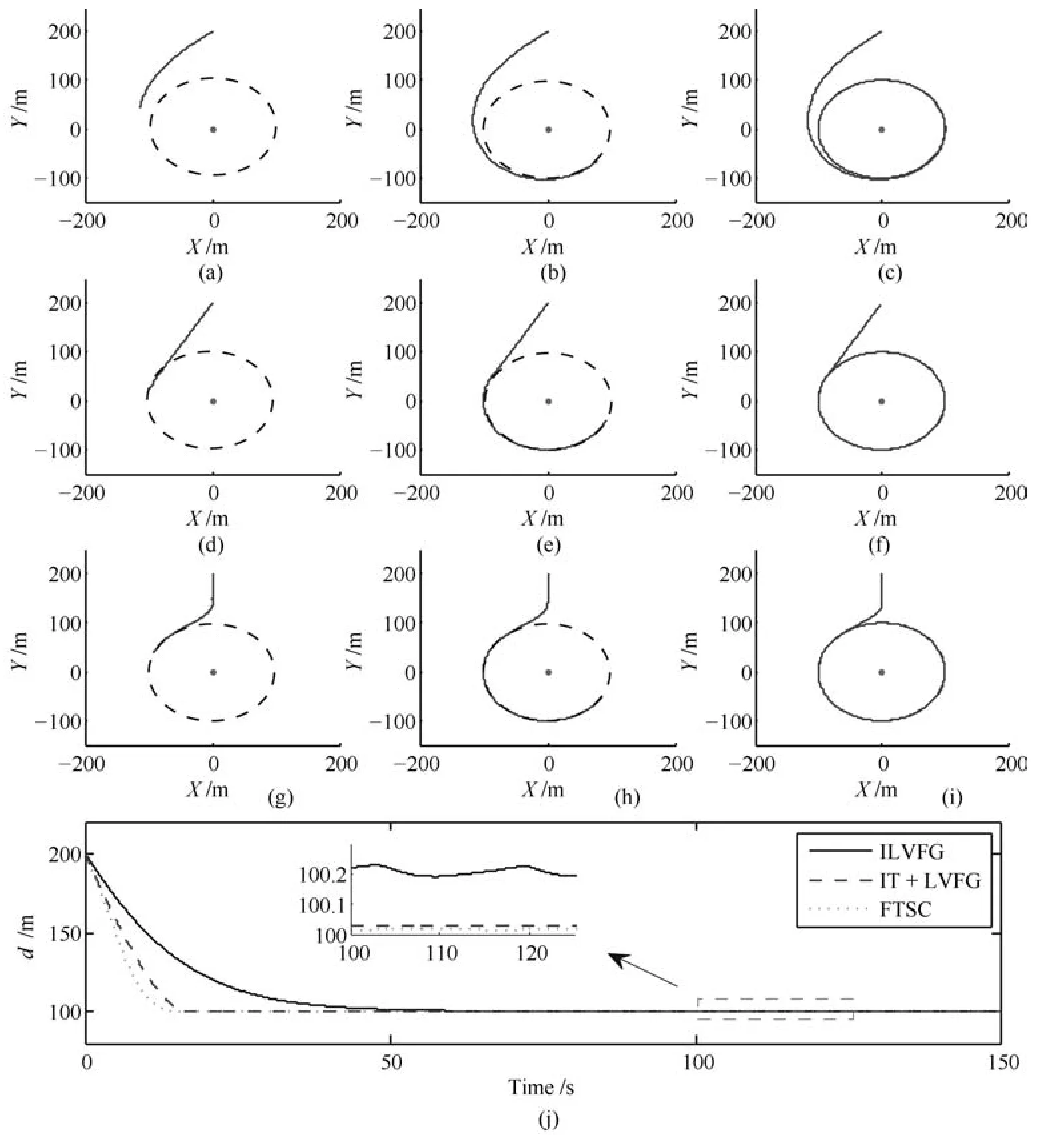
假设1.相对运动模型(5)中,0≤vt 定义1[26].考虑如下连续系统如下假设: 其中,x∈Rn,f(0)=0,f:D→Rn为一个连续函数,D⊂Rn为原点x=0的邻域,由初始状态x0=x(t0)出发的运动轨迹简记为x(t)=x(t,t0,x0). 若系统(7)满足:1)在平衡点x=0稳定;2)有限时间收敛,引入原点的开邻域D0和收敛时间函数T(x0).D0{0}→(0,∞),对任意初始状态x0∈D0{0}⊂D,若存在T(x0)>0使得t∈[0,T(x0)]时,x(t)∈D0{0}且limt→T(x0)x(t)=0;当t>T(x0)时x(t)=0,则系统(7)在平衡点有限时间稳定. 若D0=D=Rn,称系统(7)在平衡点全局有限时间稳定. 引理1[31].若存在一个连续可微的Lyapunov方程V(x):D→R满足:1)对任意x∈D0{0}⊂D,V(x)为正定函数;2)存在k∈R+和α∈(0,1),使得对任意x∈D0{0}⊂D,(x)+kVα(x)≤0.则系统在平衡点有限时间稳定.且收敛时间T(x)≤V1−α(x)/(k(1−α)). 本文旨在设计一个稳定且有限时间内收敛的无人机飞行控制器,实现在速度受限条件下对运动目标的环绕跟踪要求. 首先利用无人机和目标的几何关系设计出合理的控制器,再利用Lyapunov稳定性定理给出可行的控制器参数,然后利用饱和控制和有限时间稳定性使无人机在满足约束条件的情况下快速实现跟踪要求. 定义无人机与目标间的相对运动模型为 其中,vr∈R+表示无人机与目标之间的相对速率,ψr∈[0,2π)表示相对航向,ωr∈R表示相对角速度. 如图2所示,定义φ∈[0,2π)表示相对速度与视线之间的角度,即ψr=θ−φ−π;β(t)∈R2表示无人机到目标的单位向量,的一个单位法向量,即 定理1.对给定的无人机速度要求,只需通过调节角度变量φ,即由相应的无人机的控制速度输入 其中,相对速率为 达到控制无人机机动完成特定追踪要求的目的. 注1.由无人机运动模型(1)可知,无人机速度νo与无人机飞行控制器的控制输入量速率vo和角速度ωo存在一一对应关系,因此以无人机速度作为输入变量u是合理的. 图2 环航跟踪相对几何模型Fig.2 Guidance geometry for stando fftracking 证明.由模型(5)和模型(8)可得 n维空间中任意向量可以由n个互不相关向量表示,如图2所示,相对速度可以表示为 由式(12)和式(4)可知,无人机速度表示为式(9)是合理的.在此情况下,求解式(11)可以得出相对速率为 根据假设1,基于相对速率vr∈R+考虑,对于给定的φ,vr可由式(10)得出.即由给定的角度变量φ,可得到符合无人机速度约束条件的相对速率vr的范围.同时若无人机速率恒定为vo,可以得到唯一的相对速率vr. 根据上述控制器设计,进一步考虑如何调节角度变量φ,保证控制器的稳定性. 在无人机的速度为式(9)情况下,相对速度可以转化为 此时,在极坐标下系统输出(6)的导数为 定义距离输出误差为实际距离与期望距离的差ed=d−d0,显然,ed∈(−d0,∞),且 其中,φ∈[0,π],即取无人机逆时针环航. 定理2.在假设1下,若无人机的速度输入为 其中,Φ(0)=0,且满足 对于给定的Φ(ed),vr可由式(10)得出,则系统输出(6)在平衡点ed=0是渐近稳定的,即无人机渐近收敛到以目标为圆心,d0为半径的期望航迹上. 证明.引入一个新的Lyapunov函数 是正定的,其导数为 根据LaSalle不变集原理[32],距离误差ed收敛到不变集ed=0,=0,即d=d0. 定理1给出了考虑目标速度的控制器结构,定理2给出了保证控制器稳定的参数条件.因此由定理1和定理2可以设计出考虑目标运动状态且保证无人机收敛到期望航迹的稳定控制器. 例1.传统的Lyapunov向量场引导法(LVFG)控制方案[10],无人机期望速度为 利用本文所提方法,考虑目标运动状态,得到改进的LVFG控制方法(ILVFG).控制器为式(18),其中,控制参数 且对于给定的无人机期望速率vo和控制参数Φ(ed),vr可由式(10)唯一确定. 由ed∈(−d0,∞),可得,因此 同时又因为 所以Φ(ed)符合条件(19),由定理2,无人机可渐近收敛到期望航迹,满足跟踪要求. 例2.文献[17]提出切向量场结合Lyapunov向量场引导法(T+LVFG)的控制方案.无人机与目标相对距离小于期望距离d 利用本文方法,对文献[17]的方法进行改进(IT+LVFG).控制器为式(18),其中,控制参数 当ed<0时,显然0<Φ(ed)sgn(ed)<1;当ed>0时,Φ(ed)sgn(ed)>0,且 因此Φ(ed)满足条件(19),无人机可收敛到期望航迹. 渐近稳定的系统状态随着时间趋向于平衡点,但不能保证在有限时间内达到期望值.本节考虑如何针对控制器(18)设计适合的控制参数Φ(ed),使相对距离d在有限时间内收敛到期望距离d0,即limt→T(d)d(t)=d0,其中0 由定理2可知,无人机速度输入u中参数Φ(ed)受约束.在设计有限时间控制器时用到了不等式缩放[27],导致控制器中参量幅值偏大.若直接运用非饱和有限时间控制器则无法满足参数限制|Φ(ed)|≤1,因此结合饱和控制设计了参数受限下有限时间饱和控制器(Finite-time saturated controller,FTSC). 首先考虑非饱和下的有限时间稳定控制器. 定理3.对系统 其中,ed∈R,vr∈[vo−vt,vo+vt],Φ(0)=0.若存在k∈R+和α=p/q,0 则系统(24)有限时间内收敛到平衡点ed=0. 证明.选取Lyapunov方程(20).根据ed∈R{0}的取值分两种情况讨论. 1)ed∈(0,∞) 2)ed∈(−∞,0) 综上所述,若Φ(ed)满足条件(25),则必然存在k'∈R+和α'∈(0,1),使得对任意ed∈R{0},k'Vα0+0.根据引理1,系统(24)在平衡点ed=0有限时间稳定. 显然,定理3中必然存在ed∈(−d0,∞){0},使得|Φ(ed)|>1. 利用有限时间稳定性与饱和控制原理相结合,考虑控制参数受限情况下的有限时间稳定控制器.设计控制器参数,如图3所示. 其中,κ为(0,1]的任意常数,Φ'(ed)满足条件(25),sat(·)是饱和函数,定义为 定理4.若无人机输入控制器(18)中参数Φ(ed)为式(26),则系统输出(6)在有限时间内收敛到平衡点ed=0,即无人机在一定时间内收敛到距离目标d0的航迹上,实现环航跟踪要求. 图3 饱和约束下的有限时间稳定控制参数Fig.3 Control parameters of finite-time stability subject to saturation 证明.由饱和函数特性,显然式(26)中Φ(ed)符合对任意ed∈(−d0,∞),|Φ(ed)|≤1. 首先,证明控制器参数Φ(ed)在式(26)情况下的系统输出稳定性. 由式(18)可知,对任意输出误差ed>0,Φ'(ed)>0,由式(26),此时Φ(ed)>0;对任意ed<0,Φ(ed)<0;且ed=0时Φ(ed)=0.以Lyapunov函数(20)检验其稳定性,对任意ed∈(−d0,∞),≤0.因此,无人机输入控制器(18)中参数Φ(ed)满足条件(26),系统输出(6)在平衡点ed=0稳定. 然后,证明该系统有限时间收敛,分为两部分.系统控制器(18)中参数为式(26)时,对任意初始输出误差ed(t0)必然存在时刻t1,使得t>t1时,ed(t)∈[ε1,ε2],即相对距离收敛到一个范围内;在该范围内系统状态有限时间内收敛到平衡点,即必然存在时刻t1 1)证明对任意初始相对距离ed(t0),必然存在时刻t1>t0,使得ed(t1)∈[ε1,ε2].假设上述不成立,则存在两种情况:对任意时刻t>t0,都满足ed(t)>ε2;对任意时刻t>t0,ed(t)<ε1. a)假设对任意时刻t>t0,ed(t)>ε2. 对任意距离误差ed(t)>ε2,由不等式(19)和式(26),可以得出此时控制参数Φ(ed)=κ,输出误差导数满足,则 因此,对任意距离ed(t0)>ε2,必然存在某一时刻t1>t0,使得ed(t1)<ε2.假设不成立. b)假设对任意时刻t>t0,ed(t)≤ε1. 若ε1≥−d0,对任意距离ed(t)<ε1,由不等式(19)和式(26),可以得出控制参数Φ(ed)=−κ,输出误差导数满足,则 因此,对任意距离ed(t0)<ε1,必然存在某一时刻t1>t0,使得ed(t1)≥ε1,假设不成立.若ε1<−d0,显然对任意时刻t>t0,都有ed(t)>ε1,假设不成立. 因此,对任意初始输出误差ed(t0),必然存在时刻t1,使得ed(t1)∈[ε1,ε2].由系统稳定性可知t>t1时,ed(t)∈[ε1,ε2]. 2)证明当无人机与目标相对距离在指定区域时,必然会在有限时间内收敛到平衡点.即,若ed(t1)∈[ε1,ε2],必然存在某一时刻t2,其中,t1 已知t>t1时,ed(t)∈[ε1,ε2],根据式 (26),此时 Φ(ed)= Φ'(ed). 因此,sgn(ed)Φ(ed)≥k|ed|α,即满足非饱和约束下的有限时间控制器条件,由定理3,系统必然在有限时间内收敛到平衡点. 上述部分证明了控制器(18)中参数Φ(ed)为式(26)时,系统输出(6)在平衡点ed=0稳定且有限时间收敛,由定义1,对任意输出误差ed∈(−d0,∞),系统输出在平衡点有限时间稳定. 定理4给出了系统输出(6)有限时间稳定的参数条件.无人机在指定区域外(|Φ'(ed)|=1,|Φ(ed)|=κ≤1)时,由饱和控制器控制其收敛到指定区域内(|Φ'(ed)|<1,|Φ(ed)|<κ),而后化为非饱和有限时间控制器在有限时间内收敛到平衡点. 注2.令T1表示饱和控制器控制无人机的收敛时间(可能为0),T2表示非饱和有限时间稳定控制器的收敛时间.则T1,T2大小与初始距离d(等同于ed)和κ,k,α相关.当其他参数相同时,随着κ增大,时间T1和T2均减小,即收敛更快速;随着k增大,ε1增大,ε2减小,即非饱和有限时间稳定控制器控制范围增大,因此,收敛时间T1增大,T2减小. 例3.利用定理4给出的控制器参数条件(26),提出符合要求的有限时间饱和控制器.控制器为式(18),其中控制参数 取k1,k2∈R+,κ∈(0,1],α=p/q,0 通过与文献[10]中Lyapunov向量场引导法(LVFG)控制方案(例1)和文献[17]的切向量场结合Lyapunov向量场引导法(T+LVFG)控制方案(例2)进行比较,说明本文控制方法的优越性.为确保仿真实验的公平性,实验中目标的初始位置为原点,运动目标的速度均为νt=(2,2cos(0.01πt)+1)m/s,即目标轨迹相同;无人机航行速率保持恒定vo=10m/s,期望距离为d0=100m. 1)验证提出的控制方案的有效性.将LVFG、T+LVFG控制器方法与本文ILVFG、IT+LVFG(例1和例2中已给出具体的控制器)进行比较,仿真结果如图4. 图4(a)为传统的LVFG和本文的ILVFG控制方法下的目标和无人机运动轨迹,图4(b)则为T+LVFG和IT+LVFG控制器,图4(c)为四种控制器下的无人机与目标相对距离.由图4(c)可以看出,已知目标速度νt,使用不考虑目标速度的LVFG和T+LVFG方法,相对距离会收敛到一定范围内,即|limt→∞d(t)−d0|≤†,其中,†与γ=vt/vo∈(0,1)相关,且T+LVFG控制器收敛速度快于LVFG控制器.而本文的ILVFG和IT+LVFG控制方法,相对距离会收敛期望距离,即limt→∞d(t)=d0.显然,对于运动目标,ILVFG和IT+LVFG控制方法比传统的LVFG和T+LVFG控制方法具有明显优越性. 2)验证提出的有限时间饱和控制器(FTSC)的快速响应能力.FTSC(例3)、ILVFG 和IT+LVFG控制方法相比较.其中FTSC中参数为κ=1,k=0.1,k2=0.01,α=7/11. 注3.由于d 对静止目标,仿真结果如图5和图6所示.图5和图6分别针对d(0)>d0和d(0) 图4 目标速度对环航跟踪误差的影响Fig.4 The in fluences of the target velocity on the stando fftracking errors 图5 d(0)>d0时静止目标环航跟踪Fig.5 Stando fftracking a static target whend(0)>d0 图7和图8分别为d(0)>d0和d(0) 3)验证提出的FTSC控制方案不同参数取值对收敛时间的影响.将FTSC(例3)中不同参数κ相对比,仿真结果如图9.其中,k1=0.1,k2=0.01,α=7/11. 图9(a)~(d)分别为κ=1/4,κ=1/2,κ=3/4,κ=1时的目标轨迹和无人机轨迹,图9(e)为对应的无人机与目标相对距离.图9表明,收敛速度随κ增大而增大. 本文主要研究单无人机对单目标进行环航跟踪的问题.1)根据无人机运动特性给出一种控制器,保证无人机能根据目标运动状态调整自身运动状态,更稳定地跟踪目标.2)根据Lyapunov稳定性定理给出渐近稳定的控制器参数条件.3)考虑其参数特性,利用饱和控制结合有限时间控制,给出显式的条件选择控制器中的参数,使无人机飞行轨迹快速收敛到期望航迹.基于环航跟踪系统的广阔应用背景,下一步考虑与协同控制结合,运用到多无人机协同跟踪目标中. 图6 d(0) 图7 d(0)>d0时机动目标环航跟踪Fig.7 Stando fftracking a maneuvering target whend(0)>d0 图8 d(0) 图9 κ对无人机环航轨迹和收敛速度的影响Fig.9 The in fluences ofκon the trajectory of UAV and rate of convergence1.2 有限时间稳定预备知识

2 飞行控制器设计
2.1 几何模型


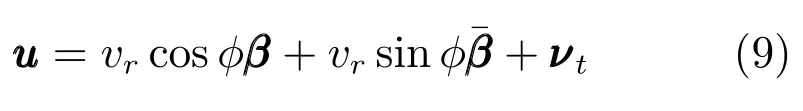





2.2 Lyapunov渐近稳定控制器



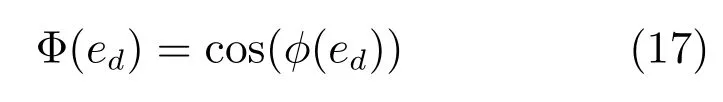
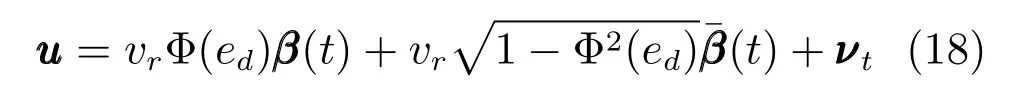










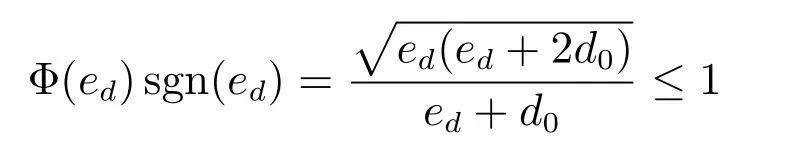
2.3 有限时间饱和控制器

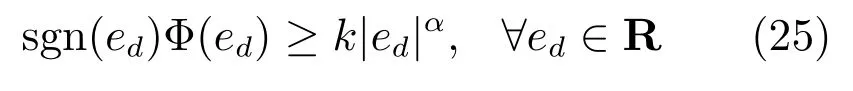





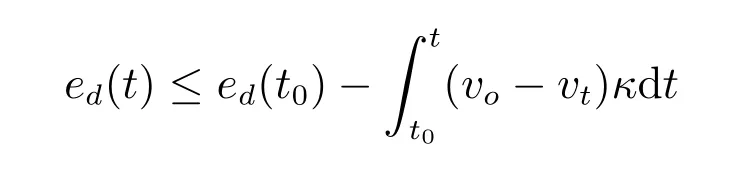


3 仿真结果及分析

4 结论






