碱式碳酸镁晶须晶胞的形成过程及其属性*

吴健松，伍思韵，林志仙，杨轶凤，赵思娜

(1.岭南师范学院化学化工学院，广东 湛江 524048；2. 岭南师范学院生物科学与技术学院，广东 湛江 524048；3. 广东省廉江中学，广东 廉江 524400)

碱式碳酸镁晶须(Mg2(OH)2CO3·3H2O)是一种新型的吸波隐形材料中的增强材料[1-2]，是制备高纯氧化镁晶须、层状双金属氢氧化物的重要中间体[3-4]。还可用作橡胶、绝缘材料、高级玻璃、及多种化工产品的添加剂和改良剂，它具有长方板状及空心管状结构[5-6]。

按衍射标准(JCPDF(73-2088)，碱式碳酸镁晶(Mg2(OH)2CO3·3H2O)是单斜晶系，空间群是C2/m，晶胞参数α=γ=90°，β=99.105；a=1.656 nm,b=0.315 nm,c=0.622 nm. 根据这些数据，碱式碳酸镁晶胞应具有如图1所示的结构。对碱式碳酸镁整个晶体而言，作者前期工作[12]证实碱式碳酸镁具有如图2所示的层状结构(由[Mg-(OH)-CO3]所组成的层称为“层板”，层板之间的水称为“层间水”)。并证明碱式碳酸镁晶须生长过程是生长基元[Mg-(OH)4]2-与H2CO3往一维方向联结的过程。

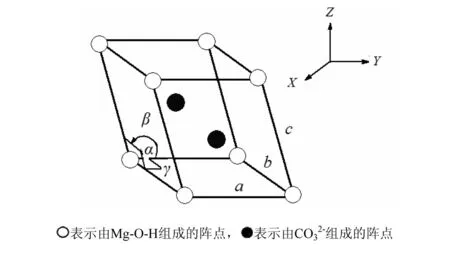
图1 碱式碳酸镁晶胞结构Fig.1 Crystal cell structure of basic magnesium carbonate

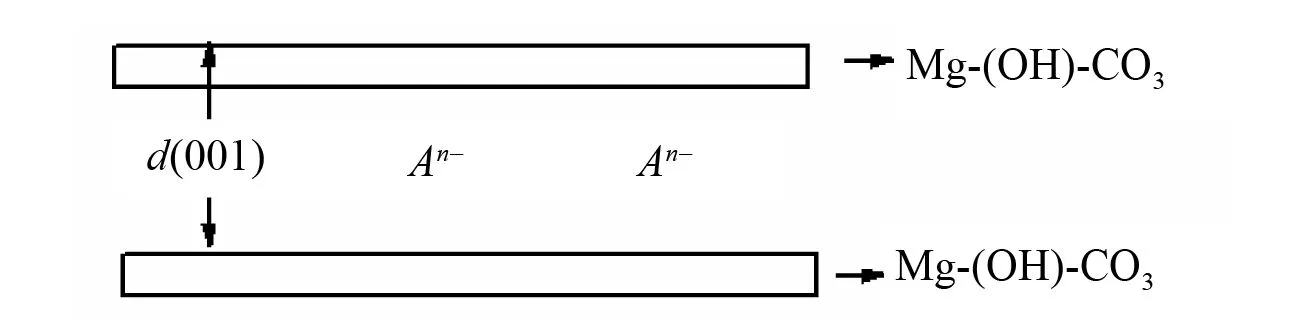
图2 碱式碳酸镁晶须的层状结构Fig.2 Layered structure of basic magnesium carbonate whisker

现本文对依据碱式碳酸镁晶须生长体系生长液拉曼数据，进一步讨论碱式碳酸镁生长基元稳定的计算、晶胞的形成过程、上述晶胞参数及对称性的由来及其属性。剖析晶胞微观形成过程及其特性，对指导人工可控晶体生长，特别是晶须的生长至关重要[7-11]。

1 实验部分

1.1 试剂与仪器

MgCl2·6H2O，NH4HCO3，均为分析纯；D/Max-3C型X射线衍射仪(日本理学Riguka,铜靶，λ=0.154 18 nm，石墨弯晶单色器)，扫描速率0.02°/s，扫描范围：10°～70°；PHILIPS-SL-30型扫描电镜；RM2000型显微共焦拉曼光谱仪。

1.2 实验过程

碱式碳酸镁晶须样品制备过程：配制2.00 mol/L的MgCl2·6H2O溶液，1.00 mol/L的NH4HCO3溶液。取2.00 mol/L的MgCl2·6H2O溶液100 mL，置于250 mL的锥形瓶内，然后在搅拌状态下滴加1.00 mol/L的NH4HCO3溶液100 mL(用3 min滴加完)，加毕，即适当取出少量(约10 mL)混合液作Raman分析。然后将混合液置于水温为38 ℃的水浴锅中水浴72 h。反应完毕，经过滤洗涤并烘干，即得到碱式碳酸镁晶须样品。

2 结果与讨论

2.1 拉曼光谱与生长基元的空间结构

拉曼光谱见图3，得到拉曼位移谱在642、1 013、1 352及1 407 cm-1处4个显著的拉曼峰，根据分子简正振动的Raman活性、偏振度并结合文献[13-15]可推知：在图3中，1 012 cm-1对应于H2CO3的C-OH伸缩振动峰，1 355 cm-1对应于H2CO3的C-O伸缩振动峰，642 cm-1对应于四面体生长基元[Mg-Cl4]2-对称伸缩振动峰, 1 407 cm-1对应于四面体生长基元[Mg-(OH)4]2-(四面体中部分羟基可部分或全部被O2-取代，下同)伸缩振动峰。这3种生长基元的空间结构绘于图4。

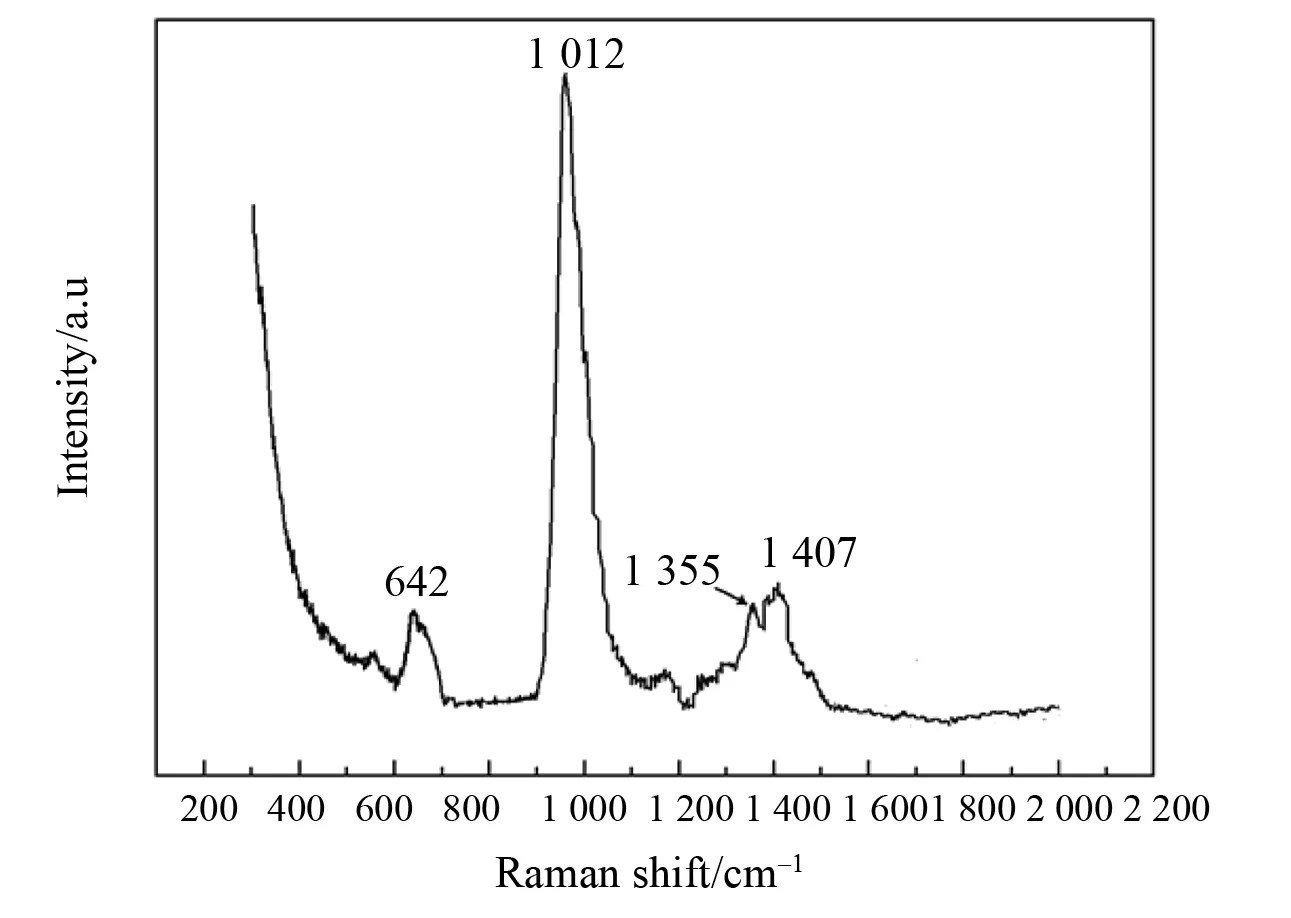
图3 碱式碳酸镁晶须生长液的拉曼光谱图Fig.3 Raman shifts of basic magnesium carbonate whisker growth solution

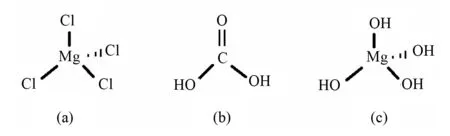
图4 3种生长基元的结构Fig.4 The structure of three kinds of growth unit (a): [Mg-Cl4]2- ; (b): [Mg-(OH)4]2-; (c): H2CO3

2.2 生长基元稳定能的计算

结合仲维卓等[16-17]提出的模型，生长基元稳定能总能量U应是以下几项之和：①静电作用能Uc；② 氢键能UBH(仅当基元可形成氢键时方有此项)；③离子色散能UD；④ 等效偶极子诱导作用能UD(仅当基元是极性时方有此项)；⑤ 等效偶极子相互作用能UK(仅当基元是极性时方有此项)。其中，第①和第②项其数值是较大的，也是起决定性作用的，其他项的数值都远小于第①和第②项，可忽略不计。

在此，以生长基元[Mg-Cl4]2-为例说明基元稳定能计算过程，由于[Mg-Cl4]2-不能形成氢键，因此，故 [Mg-Cl4]2-稳定能总能量U=Uc，依(1)式计算:

U/(J·mol-1)=Uc=

(1)

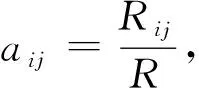
(2)

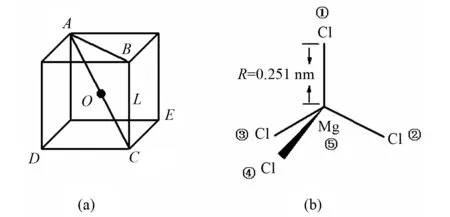
图5 [Mg-Cl4]2-四面体结构Fig.5 Tetrahedral structure of [Mg-Cl4]2-

a12=a13=a14=a23=a24=a34

即：

Z1=Z2=Z3=Z4=1

Z5=2

V51=V52=V53=V54

而

即：

V52=V53=V54=2

V12=V13=V14=V23=V24=V34

而

即：V13=V14=V23=V24=V34=0.612

6V12+ 4V51=6×0.612 + 4×2=11.672

再将此值代入(3)式，即得：

U= 54.007 7 J/mol

上述是生长基元[Mg-Cl4]2-稳定能的计算过程，其他基元稳定能计算过程与此基本是一致的，只是有些参数要改变。现将稳定能计算各参数来源列于表1，后文遇到稳定能计算时，只须将相应的参数依具体基元的实际作修改即可。

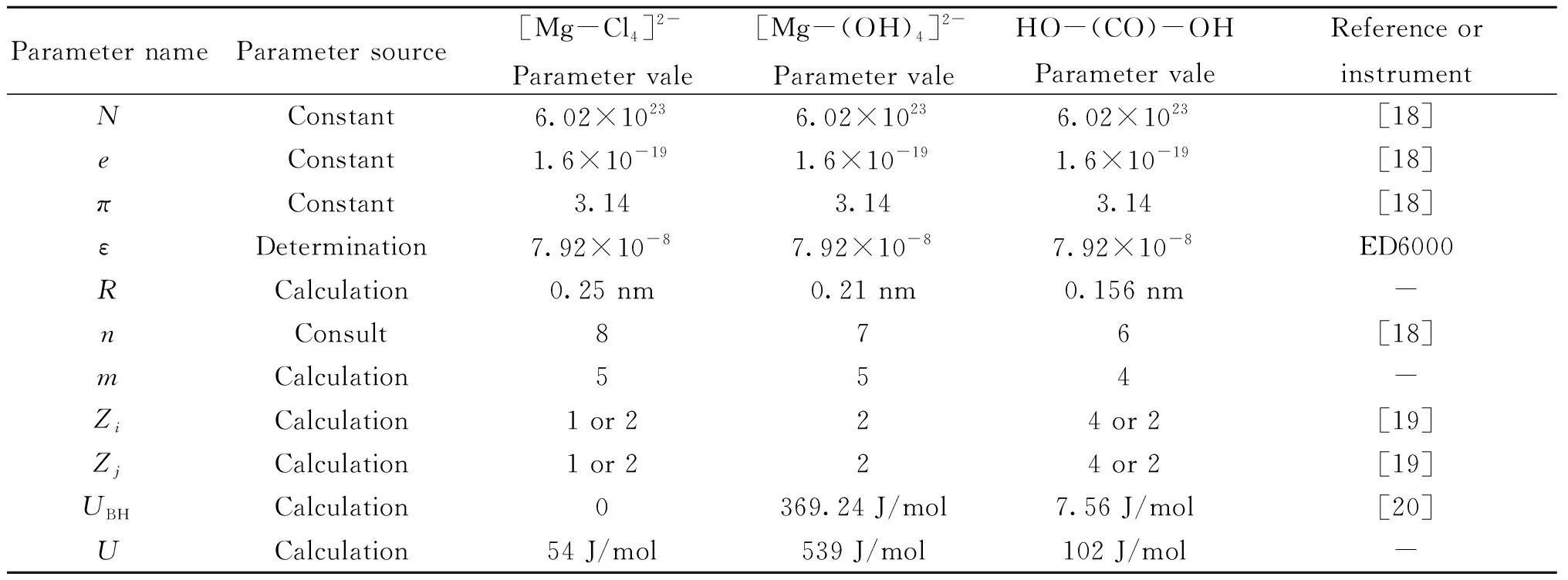
表1 计算稳定能各参数来源Table 1 Sources of calculated stability energy parameters

对于也是正四面体结构的生长基元[Mg-(OH)4]2-稳定能的计算，其R值、Z值和n值均与[Mg-Cl4]2-不同。[Mg-(OH)4]2-基元中镁氧距离R=0.21 nm，氧的电荷数Z=2，玻因常数n=7，将此2个参数代入(2-2)式和(2-3)式，同理可算得Uc=169.737 1 J/mol。又因[Mg-(OH)4]2-基元相互之间有氢键，所以[Mg-(OH)4]2-总的稳定能还必须加上氢键键能此项(对于氢键键能的计算(可依文献[20]计算，在此不作述及)，最后计算得[Mg-(OH)4]2-总的稳定能为539 J/mol。生长基元H2CO3是平面三角结构，比四面体结构要简单，其碳氧键长R=0.13 nm，同样是按上述方法，可算得总的稳定能U= 102 J/mol。计算结果表明，[Mg-(OH)4]2-和H2CO3的稳定能较大，[Mg-Cl4]2-稳定能较小，因此，[Mg-(OH)4]2-和H2CO3是有利生长基元，在生长过程中是主要的联结对象，故碱式碳酸镁晶须的化学组成只有这2种基元所含有元素的化学组成。

2.3 碱式碳酸镁晶胞的形成过程

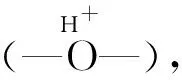
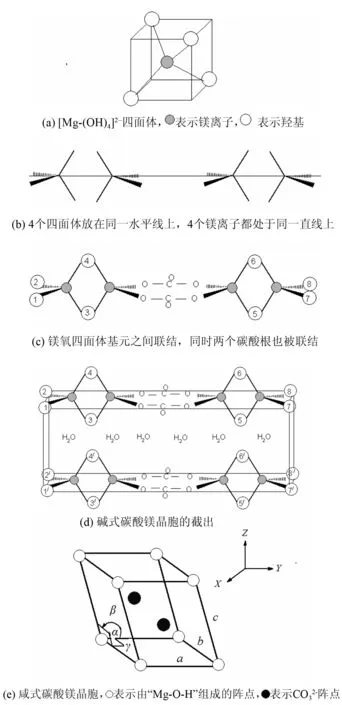
图6 碱式碳酸镁晶胞的形成过程Fig.6 Formation process of basic magnesium carbonate cell

根据晶体是阵点在三维空间延伸的特性，将图6(c)所示的基元联结后的结构复制一次，并置于其下面，且在它们两者之间排上6个H2O分子。又为了作区别及方便讨论，将复制出的那部分的羟基数字加上一撇，见图6(d)。如果用一个平行六面体将图6(d)截分，截分的方式如图所示，如：平面1 782(就用羟基的数字表示六面体的顶点)平分羟基1、7、8、2，且平分2个碳酸根及4个镁离子(其他平面的对基团的截分见图示，不再一一罗列)。则六面体17 828′7′1′2′便可抽象为碱式碳酸镁晶胞，如图6(e)所示，此晶胞与JCPDF(73-2088)记录的碱式碳酸镁晶胞是高度吻合的。这可从晶胞参数的数值、晶胞对称元素、化学组成3个方面得到证明。

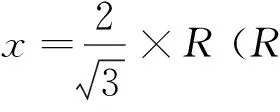
即a=4x+0.59=4×0.243+0.59=1.562 nm

6个H2O的长度(每个H2O的长度约0.28 nm)之和为1.68 nm，也与a值接近)。现将各计算结果列于表2，并将JCPDF-73-2088的数据一并列于表中作比较。

从表2可知，本文推断的碱式碳酸镁晶胞在晶胞参数、化学组成及对称性与JCPDF-73-2088是高度吻合的，下面对表2中晶胞数据来源继续作分析讨论。

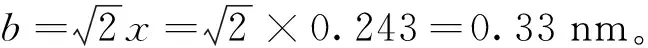
图7 碱式碳酸镁晶须的SEM图Fig.7 SEM images of basic magnesium carbonate whisker(圆圈内为易滑动迹象)

Cell parameters, chemical composition and symmetry elementsThe basic magnesium carbonate cell deduced by this paperJCPDF-73-2088RDCell parameters a1.562 nm 1.65 nm5.33%b 0.33 nm0.32 nm3.12%c 0.61 nm0.62 nm1.64%α90°90°0β>90°99.15°-γ90°90°0Chemical composition Mg2(OH)2CO3·3H2OMg2(OH)2CO3·3H2O0Symmetry elementsSymmetry axisL2L20Symmetry planeMM0

图8 碱式碳酸镁晶须的XRD图Fig.8 XRD of basic magnesium carbonate whisker

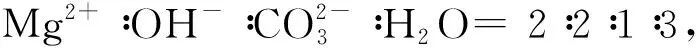
图9 碳酸根抽象为一个阵点的过程Fig.9 The process of abstract carbonic acid into a position

3 结 论

对于碱式碳酸镁晶须，从其生长液拉曼数据确定生长基元空间结构后，根据基元几何结构，再结合稳定能的算式可准确地计算出生长基元稳定能；根据基元的结构特点及联结方式，再结合空间点阵抽象，可准确地推导出晶胞的形成过程及其结构特点。这些计算方法可为其他从液相体系生长的晶体晶胞计算提供借鉴。