“电路”课程教学与审美

董维杰， 白凤仙

(大连理工大学 电气工程学院， 辽宁 大连 116023)

0 引言

在对工科学生教育的过程中，很多教师会特别注重学生的逻辑思维能力、发散思维能力和理论联系实际等能力的培养，但是，很少有人会注意到学生审美能力的培养。

美是能够使人们感到愉悦的一切事物，它包括客观存在和主观存在。美是要去体验、去感受、去欣赏，这就是审美。法国著名雕塑家罗丹说过：“世界上不是缺少美，而是缺少发现美的眼睛”，此话道出了审美的真谛。

“电路”课程讲的是电路元件连接起来所组成的电路的基本规律、基本定理和电路分析方法，电路作为客观世界的物质存在，其电压、电流运行规律蕴含了自然界的简单美、和谐美和对称美，教学过程中教师可引导学生体会那些美。上海交通大学田社平老师从电路名称之美、电路理论之美、电路应用之美到电路研究之美，全面讨论了电路之美，令人耳目一新[1]；南京邮电大学周井泉教授则重点论述了电路的对偶之美[2]。

1 电路教学中审美训练的意义

审美能力，就是人们认识美、评价美的能力，包括审美感受力、判断力、想像力和创造力等。在学习中，如果能够有发现美的能力，必将促进学生的学习兴趣，促进学生想象力和创造力的发挥。学生认识了电路中的美，可形成对电路更为深刻的认识，提高分析和设计电路的能力。

马克思说：“人类是按美的规律去改造世界的”，在工作中，较高的审美能力，可以让我们更容易以富于想象力和创造力的方式解决实际问题。在科学发现和技术创新的道路上，处处存在着美的足迹。法国著名数学家阿达玛说：“科学美感，这种特殊的美感，是我们必须信任的向导”，因为“唯有美感预示着将来的研究结果能否会富有成果。”这其实给了科研工作者一个重要的判据，如果模型或计算效果是复杂、不和谐、无秩序的，基本可以断定是错的。

2 电路中的美与审美

2.1 简洁美

画家郑板桥的艺术创作心得“删繁就简三秋树，领异标新二月花”，向人们展示了简约美的意境：以最简练的笔墨表现最丰富的内容，以少胜多。简洁美，有朴素、简单的外在形式，通过极度浓缩精炼，包罗万象寓意深远。

电路中基尔霍夫定律、欧姆定律的数学表达式都极简洁的。基尔霍夫电流、电压定律的内容是：在集总参数电路中，在任一时刻，流出或流入任一节点或封闭面的各支路电流的代数和为零；沿任一回路巡行一周各元件上电压降的代数和为零，如式(1)、(2)所示。欧姆定律内容：线性电阻元件两端的电压与流过的电流成正比，如式(3)所示。

Σi(t)=0

(1)

Σu(t)=0

(2)

u=Ri

(3)

在德国发行的基尔霍夫纪念邮票上，清晰印着式(1)和(2)，彰显了基尔霍夫的科学贡献及定律的重要地位，如图1所示。

图1 基尔霍夫纪念邮票

基尔霍夫电流定律反映了电荷守恒定律，基尔霍夫电压定律反映了能量守恒定律。欧姆定律表述形式不仅适用于线性电阻，还可推广到正弦稳态电路中电容、电感、阻抗的复频域电压电流关系，在电学史上具有里程碑意义。式(1)～(3)的美在于电路规律的数学表达形式是何等简洁，但是反映的电路运动规律却内涵深刻，并且适用于千变万化的集总参数电路，是贯穿整个“电路”课程的理论基础。

基尔霍夫定律去除电路元件和结构千变万化的表面现象，揭示了电路的本质和内在规律，是等效变换、支路法、节点法、回路法、割集法等各种电路分析方法列方程的依据。但是当分析具体电路时，又要针对复杂多变的电路把简洁的表达式变成规模、系数、变量不同的方程组，直流电路对应实数代数方程，正弦稳态电路列出的是复数代数方程，电动态电路对应微分方程。在分析各种具体电路时，要掌握基尔霍夫定律的本质，如果死记具体电路的特殊方程形式，则不能举一反三，可能会导致错误不断。

以下图为例说明不管电路如何千变万化，把握KCL定律简洁本质的重要性。

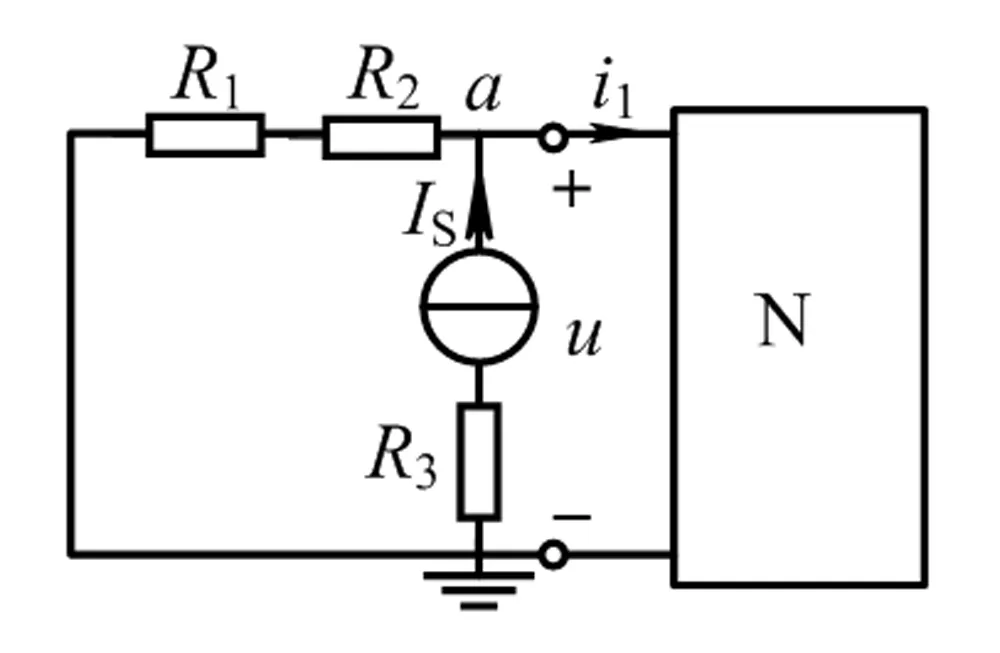
图2 列写节点电压方程易错电路示例

图中节点a只有三条支路，而三条支路组成完全不同。节点电压方程归根到底是列KCL方程，本质是三个支路电流代数和为零。节点a的电压方程是

刚开始学习节点电压法时，学生容易错写为

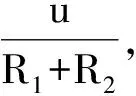
科学就是去粗取精、去伪存真，提炼复杂问题的本质，而对事物本质的描述大多是极其简洁的；再用抽象出来具有简洁形式的原理来指导解决复杂问题。在基尔霍夫定律、欧姆定律的教学中，我们让学生体会这一科学方法论，潜移默化中培养其科学发现的意识、学习科学研究方法。

2.2 和谐美

和谐美是指事物发展中均匀流畅、协调有序、多样统一的美。

正弦稳态电路分析中，旋转相量在复平面内做周期性匀速圆周运动，向实轴投影出余弦函数表示形式的正弦波，向虚轴投影出正弦函数表示形式的正弦波，如图3所示。正弦波用旋转相量的初始位置相量表示，正是相量分析法的基础。正弦波形是正弦稳态电流强度或电压大小随时间变化的波形，正弦电路中自由电荷在热运动基础上做微米级振幅的单摆运动，振动位移也是正弦波形，简谐运动是最基本也是最简单的机械振动。无论旋转相量转动投影映射成正弦波、自由电荷的单摆运动本身、还是示波器测量到的正弦电压电流波形，无不呈现出均匀流畅、规律有序的美感。

图3 旋转相量在实轴上的投影对应于正弦波

用相量法分析正弦稳态电路，求网络函数、阻抗、分压分流都涉及相量的乘法和除法运算，此时相量宜用极坐标或指数形式表示。相量指数形式即为欧拉公式ejθ=cosθ+jsinθ，它的神奇之处在于沟通了三角函数与指数函数之间的内在联系。当θ=0时，有ej0=cos0+jsin0=1，其数学意义完全不同于e0=e1/e1=1。当θ=π时，有

ejπ+1=0

(4)

数学家们爱把式(4)视为最优美的公式，美在哪里呢？它将代数中的虚数“j”、几何中的圆周率“π”( 3.14159，无限不循环小数)、高等数学中的自然常数“e”(2.71828，无限不循环小数)、数学和哲学中最重要的“1”和“0”两个数字神奇地统一在了一起，惊人地体现了统一美。有了这些铺垫，相信在复数阻抗串并联、电压电流相量算术运算中涉及到直角坐标与指数形式相互转换时就不易犯错。

2.3 对称美

对称是自然界的一种普遍现象，植物、动物和人都有自己的对称形式。对称美来源于自然界物质形态及其运动图景所具有的广泛对称。对称之所以让人产生美感，是因为对称中存在着某种“重复”、“均衡”和“有序”。

很多科学家也是因为坚信宇宙美具有对称性这一特点，作出了许多划时代意义的科学发现。例如，物理学家保罗.狄拉克正是由对称美出发,通过狄拉克方程(电子运动的相对论性量子力学方程)预测了反电子的存在，提出了反物质概念。可见审美意识也是发现和创造的基础。“大学物理”中介绍的麦克斯韦方程组被公认是很美的，因为它揭示了自然的对称性，完成了物理学的第一次统一。

1971年，加州大学伯克利分校的蔡少棠教授考察电荷、电流、电压、磁链这四个电路基本变量之间的关系时，总结四个变量定义了电阻、电容和电感三大标准元件，发现连接电荷和磁通量的元件缺失了，因此预测了第四种基本电路元件，叫做“忆阻器”，其英文名称Memristor是memory 和resistor的组合，暗示其具有记忆和电阻的双重作用，如图4所示。直到2008年惠普的工程师团队才制作出器件，器件模型表明忆阻器先天是纳米尺度器件，因此有望在高密度存储器和人工智能方面大放异彩。这是对称美、完整美在科学发现方面的又一次亮相，如果没有忆阻器补全那个位置，那么图4看起来就有不能释怀的缺憾。

图4 忆阻器存在的预测依据

电路中的对称美比比皆是，例如：“共轭”概念蕴含着“对称”性，“对偶”关系也可视为“对称”的一种形式。

表1 常见对偶元素

电路的这种对称美是宇宙美具有对称性的一个典型例证，也为电路知识点的学习提供了捷径。利用对偶原理可以将已知电路或元件的数学关系式直接推广到其对偶元素，这样既简化了分析过程，又提高了学习效率。例如，由电导并联时的分流公式可以直接得出电阻串联时的分压公式；将戴维南定理表述中的“电压”、“电阻”、“开路”等替换成对应的对偶元素“电流”、“电导”、“短路”就得到诺顿等效定理；将节点电压方程中的“电导”、电压变量和电流源换成“电阻”、电流变量和电压源就得到回路电流方程；讲了电容元件的时域、频域电压电流关系后，利用对偶原理可直接推出电感元件的电压电流关系。

2.4 思辩之美

发散思维是从一个目标出发，沿着各种不同的途径去思考，多方位、多角度、多层次去思考。“横看成岭侧成峰，远近高低各不同”，横看侧看变换角度，乐此不疲，因为能够欣赏到不同的美景。当人们观察事物的立足点、立场不同时，就会得到不同的结论，综合这些结论，便形成对事物更完整的认识。这种全面的、辩证的、多角度的思维具有思辨之美。一场引人入胜的辩论赛，一篇通透深刻的说理文章，往往胜在具有思辨之美。

“电路”课程的重要内容是电路分析方法，一个电路可用多种方法求解，希望学生能够在学习过程中体会到思辨之美。

对于结构上存在元件串并联的电路，某一支路电压、电流或功率的求解，几乎可以用遍所有的电路分析方法。这些方法视角不同，有的从整体，有的从局部；有的具有普适性，有的是具体问题具体分析。

如图5所示电路，求3 Ω电阻两端的电压U。此题可用下述六种方法求解。

图5 多种方法求解电路例题

方法一，支路电压法，以U为变量列写KCL和KVL方程。方法二，对12 V电压源、1 Ω电阻和2 A电流源做串并联等效变换。方法三，节点电压法，若以下面节点为参考节点，则可选一个独立节点①，也可选①和②作为两个独立节点。方法四，回路电流法。方法五，应用叠加定理，令12 V电压源和2 A电流源分别单独作用。方法六，应用戴维南定理，求移除3 Ω电阻后的单口网络的开路电压和等效电阻。

叠加定理、戴维南定理、替代定理、互易定理等的综合应用充满了思辨之美，文献[3]中一道例题给出了三种解题方法，该书第一版更是给出了五种方法，其中有的方法是学生的贡献。

这一道例题把几乎所有的电路分析方法都一一用到，在对比中体会不同方法的精妙，领会基尔霍夫定律和欧姆定律的应用，感受条条大路通罗马的妙处，惊诧于曲径通幽的过程，这就是思辨之美带来的精神愉悦。笔者经常建议学生以这样的方式来复习，很有成效。

3 结语

在“电路”课程的教学中介绍电路之审美，引领学生体会自然界的简洁美、和谐美和对称美在电路中的表现，在讲述电路分析方法的同时让学生感受思辨之美，希望学生通过本课程锻炼自己的审美能力，在美的感受中愉快学习，并在今后的学习和工作中，用美的感觉去发现世界、创造世界。