垂直型固定式测斜仪在安徽省阳台滑坡监测中的应用

蔡志川，向 钒

（安徽省地质调查院，安徽·合肥 230001）

滑坡是岩土体沿着贯通的剪切破坏面所发生的滑移地质现象。在美国，每年滑坡带来约10～20亿美元的经济损失和25～50人死亡。意大利在1279～1999年期间840次滑坡中的死亡人数超过1万人。我国是滑坡灾害多发国家，据统计，1949～2011年期间，由滑坡造成的经济损失平均每年约为5000万美元[1]。2012～2017年我国共发生滑坡地质灾害约35000起，占总体灾害的68.62%。

为发现隐患，消除灾害，须对各种山体滑坡进行有效而经济的监测。滑坡变形是滑坡地质结构及内外影响因素的综合反映，滑坡变形监测是分析滑坡地质结构、变形动态的依据，是滑坡整治工程信息化设计及灾害预测预报的可靠技术保障。其中滑坡深部位移监测是滑坡变形监测的重要内容，对准确确定滑面位置，研究滑坡目前性状与发展趋势，以及整治工程设计可提供重要信息[2]。测斜仪监测的原理是根据铅垂受重力影响的结果，测试测管轴线与铅垂线之间的夹角，从而计算出钻孔内各个测点的水平位移与倾斜曲线[3]。本文以基康公司BGK-6150MEMS垂直型固定式测斜仪系统为例，介绍该仪器的传感原理及测量原理，并结合安徽省休宁县阳台滑坡实时安全监测预警的应用，说明其在变形监测中的实际效果。

1 测斜仪工作原理及布置

1.1 BGK-6150垂直型固定式测斜仪系统简介

基康仪器（北京）有限公司BGK-6150MEMS垂直型固定式测斜仪系统，可用于长期监测大坝、基础墙、边坡、挡墙等类似建筑的分层水平位移变形，或者单独安装时用于测量建筑物或结构的倾斜变化。

监测采用钻孔方式并安装测斜管，并在测斜管内不同高程安装倾斜传感器，可获取滑坡内部不同高程的水平位移状态，并通过无线数据传输至客户端接收。这种应用可方便地实现远程遥测，并可准确而连续地监测滑坡内部及剖面的变形情况。

1.2 BGK-6150垂直型固定式测斜仪系统工作原理

（1）监测仪器数据处理转换倾角变化测量按照下式计算：Δθ=arcsin(G×(R1-R0))

式中：G-仪器系数，由率定表给出；R1-当前读数；R0-初始读数

设一测斜仪的安装长度为L（图1），当相对于O点产生角度为θ的倾斜（转动）后，A点位移到A′，则有D=L×sinθ。

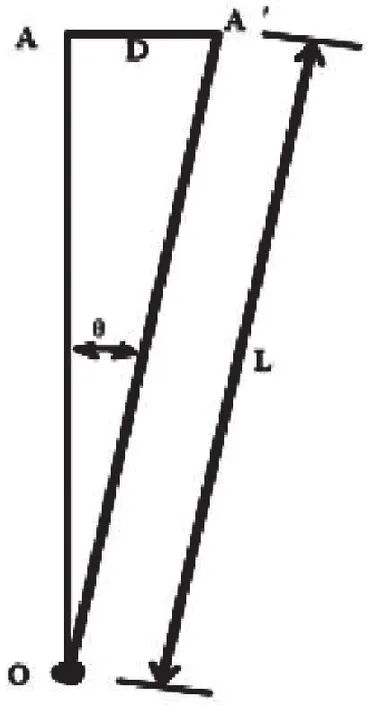
图1 水平位移换算原理Fig.1 Conversion principle of horizontal displacement

多支测斜仪串联后，将这些仪器产生的位移变化量进行累加即可获取整个剖面的垂直位移变形曲线。以铅直向安装的5测点固定式测斜仪为例（见图2），假定以L1端为基准，则L5端在垂直方向产生的总位移量：

D=D1+D2+D3+D4+D5

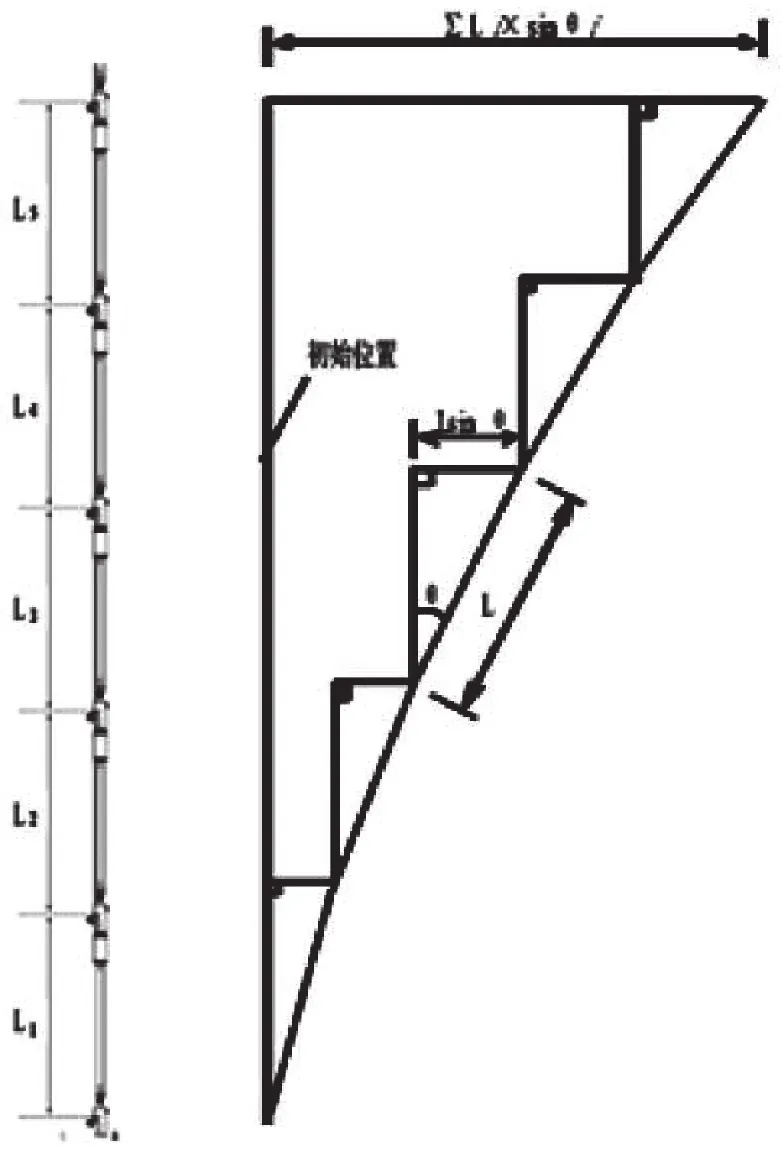
图2 倾斜到沉降转换示意图Fig.2 Schematic diagram of inclination to settlement transformation

（2）监测数据接收

数据自动监测的基础上人工自定义监测，自动监测设定时间灵活，可设置为每小时一次、两小时一次等，通过GPRS网络实现异地接收数据（图3）。

图3 数据实时监测系统Fig.3 Actual time data monitoring system

1.3 测斜仪系统仪器布置

监测仪器平面上布置安置选取的位置应兼顾变形最大区域及高威胁区域（图4）。

钻孔施工可知滑坡基岩埋深35～46m，仪器垂向安置定位原则为：钻孔中取芯率低区域及钻孔内碎石与黏土交界区域（表1）。

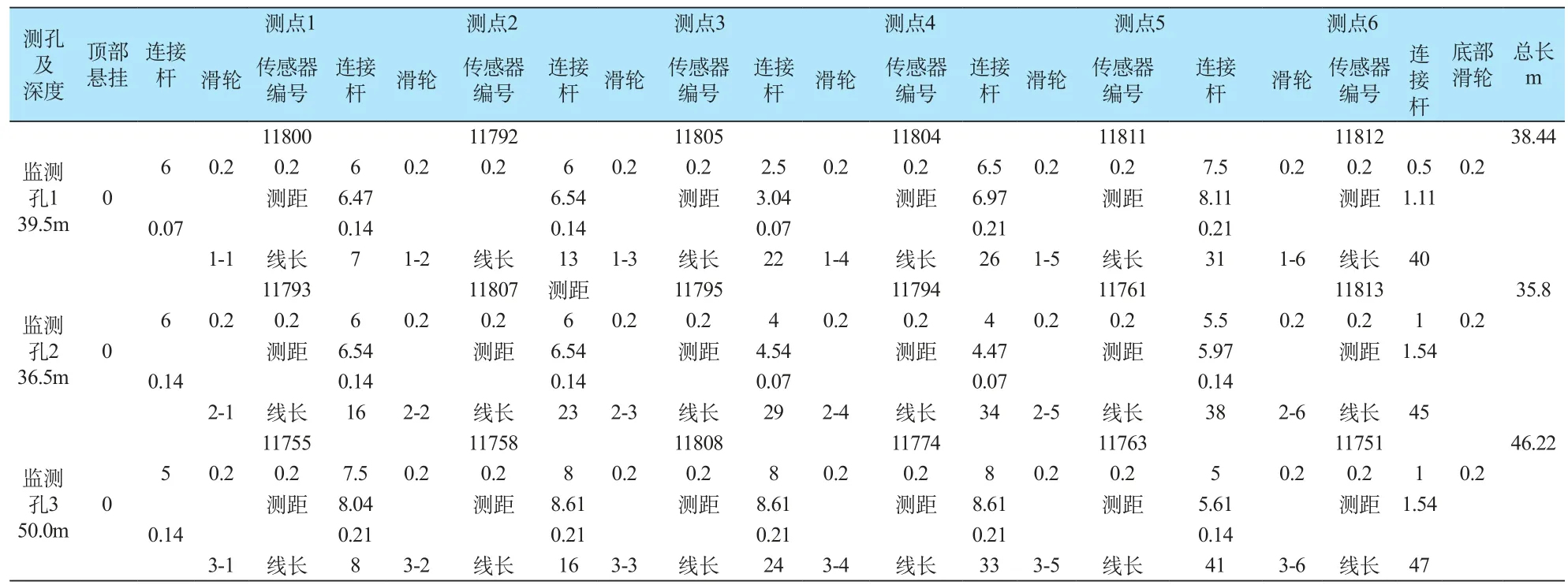
表1 监测孔仪器安置情况Table 1 Instrument placement for monitoring hole

2 测斜仪数据采集及分析

2.1 监测数据分析

结合工程实践研究发现，对研究滑坡变形有意义的曲线主要有以下几种：累积位移-深度曲线，即累积位移随深度的变化；相对位移-深度曲线，即相对位移随深度的变化；位移矢量-时间曲线，即同一测点在不同时刻的位移矢量变化；位移-时间曲线，即位移过程曲线，又可分为累计位移或相对位移过程曲线；位移矢量-深度曲线，即同一时刻不同深度的位移矢量变化。

本次工作对于滑坡数据分析采用累积位移-深度曲线、位移矢量-时间曲线、相对位移-时间曲线三种进行分析。

（1）累积位移-深度曲线

滑坡深部累积位移-深度曲线位移变形有“V”形、“D”形、“B”形、“r”形、“钟摆”形及复合型等几种曲线形态，每种曲线形态可反映滑动面 (或潜在滑动面 )的位置和滑坡变形发展过程，同时可反映滑坡的滑动性质。当形态呈“钟摆”形时,滑坡处于相对稳定阶段；呈“V”形、“B”形时，滑坡处于潜在滑动阶段；呈“D”形、“r”形，且位移速率较大时 ,滑坡处于失稳破坏阶段[4]。

图4 监测仪器布置图Fig.4 Arrangement diagram of monitoring instruments

根据图形分析（图5）可知：监测孔1、监测孔3属于“V”型，曲线特点表现为，底部位移很小，而上部位移较大，中间没有较明显的波峰和波谷 (滑动面)， 表明滑坡该部位还没有形成明显的滑动面，处于剪切蠕变阶段，但随着时间的推移，有可在最薄弱的地方形成滑动面。

监测孔2属于“钟摆”型，即不同时刻的位移-深度曲线在初测值两侧作小幅度摆动，摆动幅度一般＜0.4mm，在量测综合误差影响范围之内，表明监测孔2附近滑体处于相对稳定状态。

（2）位移矢量—时间曲线

选取监测孔3，数据时间为2012年3月至2014年3月，根据位移矢量-时间曲线可知，在2012年10月31日位移矢量时间曲线曲率明显变小，意味着在这个时间之后，仪器不再发生明显的位移，仪器附近滑体处于相对稳定状态（图6）。

（3）相对位移—时间曲线

选取监测孔3，数据时间为2012年3月至2014年3月，由相对位移-时间曲线图可知，2012年3月至2012年10月，位移值从0.34mm降至0.0004mm，逐渐趋于稳定。仪器在2012年 10月31日左右位移趋于稳定。而后一直在正负0.001之间振动，未发生明显位移（图7）。

2.2 监测数据分析结论

通过对第一种曲线的分析判定各监测孔附近坡体堆积物的稳定性，初步可知监测孔1、监测孔3两孔累计位移和深度呈反比，两孔附近坡体堆积物处于相对不稳定状态，有发生蠕滑变形的可能性，监测孔2监测孔附近坡体堆积物处于相对稳定状态。通过对第三种及第四种曲线的分析可判定监测孔附近坡体堆积物的稳定性现状，分析可知仪器安装至自2012年10月，监测孔3最大累计位移位置位于地表，发生的累积位移量为0.46mm，其中2012年7月—2012年9月仪器附近的位移量变化最为明显，表现为累计位移—时间曲线斜率增大。2012年9月—2012年10月底，仪器附近位移增加速度变缓，表现为累计位移—时间曲线斜率变小直至近水平以及相对位移—时间曲线纵坐标区域0附近振动。

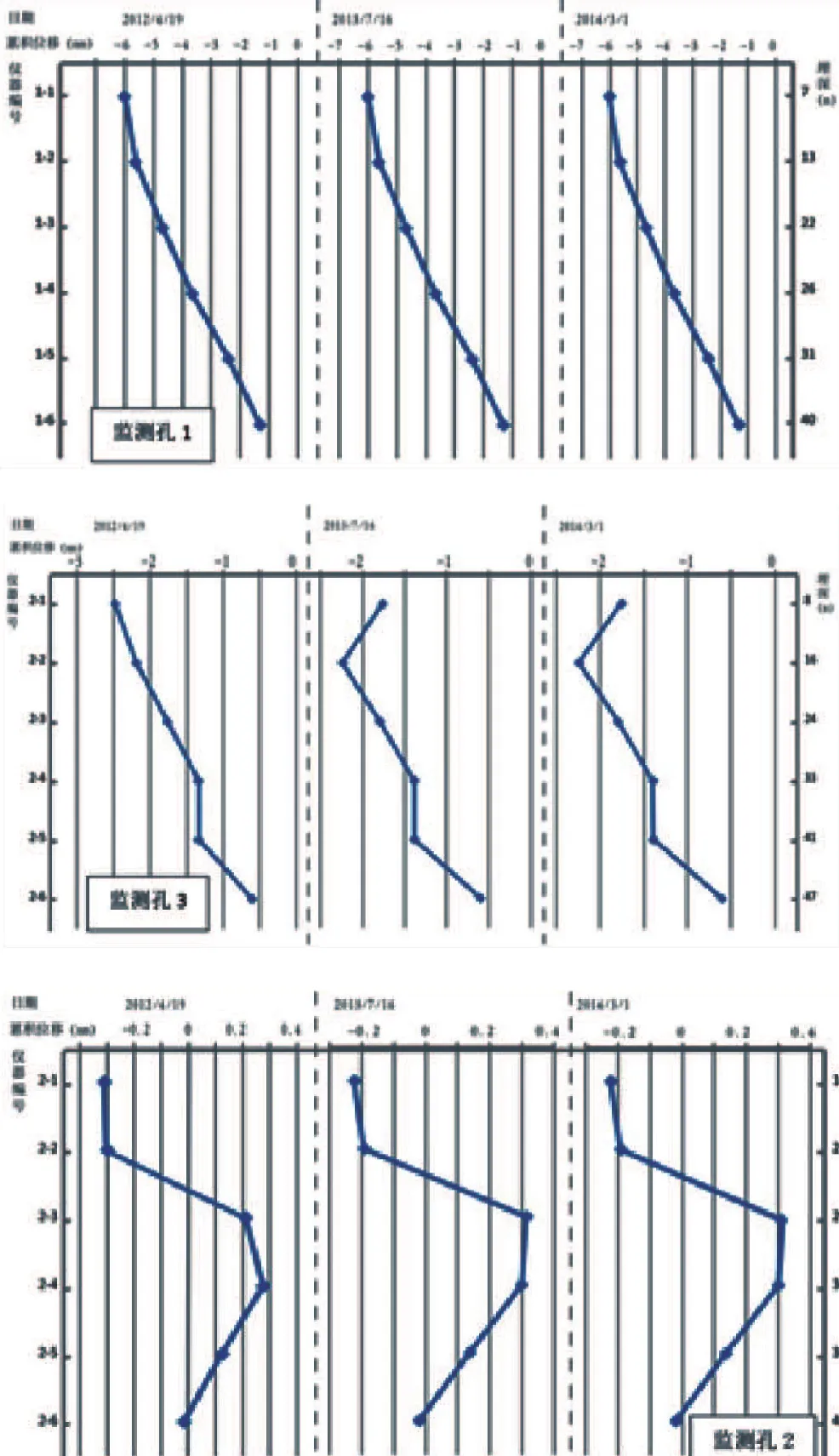
图5 累积位移—深度曲线Fig.5 Accumulate displacement-depth curve

图6 位移矢量—时间曲线Fig.6 Displacement vector-time curve

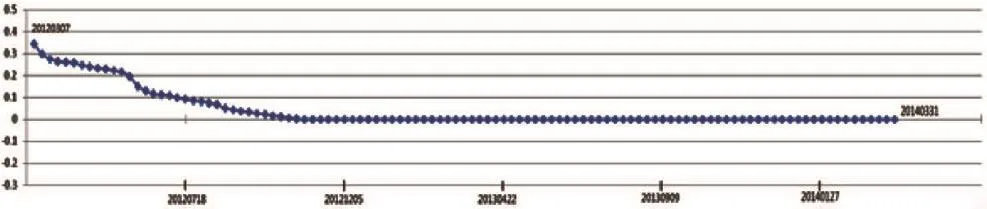
图7 相对位移—时间曲线Fig.7 Relative displacement-time curve

通过分析认为仪器安装初期，由于钻机成孔及仪器套管安放，对坡体地应力产生了影响，仪器成孔直径为89-127mm，套管为直径75mm的ABS管，安放结束对仪器套管周围进行回填，回填材料为碎石土。初期由于钻孔内地应力变化以及回填土内碎石的重力压实作用，仪器位移变化较明显，尤其在雨季2012年7月—2012年9月，由于地表降水入渗，导致坡体堆积物及回填土内应力发生变化，直接表现为该时间段累计位移-时间曲线斜率变大。直至2012年10月底，仪器已安装约7个月，填层已密实，内部地应力趋于稳定，因此10月31日后监测孔地表累计位移趋于平缓，直接表现为相对位移在0附近振动。说明仪器附近滑体一直处于相对稳定状态。

3 结论

本文通过对滑坡的内部变形监测成果进行分析，结合滑坡的地质勘查情况，得出如下认识：

（1）通过对垂直型固定式测斜仪数据成果的分析，可以有效判定地表下最危险滑动面的范围，有利于分析边坡的变形机制，能够为治理设计提供可靠依据。

（2）通过数据的长期监测，能够预测边坡滑动变形的趋势，结合边坡稳定性分析成果，可为防灾预报和应急治理提供信息。

（3）监测数据可在自动监测的基础上人工自定义监测，并通过GPRS网络实现异地接收数据，实现了灾害点的动态监测。实践证明，垂直型固定式测斜仪的使用是滑坡深部位移监测研究行之有效的手段。