基于GPS伪距观测值的三种随机模型比较

何维卿，刘 昶

（1. 安徽省地质矿产勘查局327地质队，安徽·合肥 230011；2. 合肥市测绘设计研究院，安徽·合肥 230000）

基于伪距和载波相位观测值所确定的函数模型确定后，通过不同方法确定随机模型可以提高待定点的定位精度。其中具有代表性的模型有等权模型、基于高度角的随机模型和基于信噪比的随机模型[1-3]。但是基于伪距观测值的随机模型研究还没有涉及[4]。本文基于卫星高度角、信噪比与GPS观测值质量之间的关系，具体探讨关于利用卫星高度角和信噪比信息所建立随机模型，并以伪距观测条件下的单点绝对定位与相对定位模式来探讨基于卫星高度角的随机模型与基于信噪比的随机模型。针对在GPS不同定位模式下所确定的随机模型对点位精度的影响，采用了从理论研究和具体案例数据处理的试验过程。

1 基于伪距观测值的三种随机模型

1.1 等权随机模型

等权随机模型将所有观测量的精度视为相同，即其先验中误差均相同[1]。由于假设了每个测站对于每颗卫星的观测值是独立的、等精度的观测量。设伪距观测量为ρ′，其单位权方差为σ2，E为单位矩阵，则非差单点绝对定位观测值的方差协方差阵为Dρ′=σ2·E，为了计算简便，我们假设单位权方差为1，则可知：

在伪距观测条件下相对定位一般采用的是双差观测值模型，基于伪距的观测方程为：

则单差观测方程为：

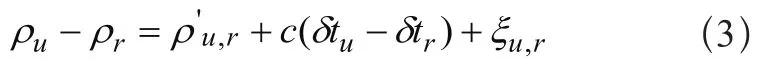
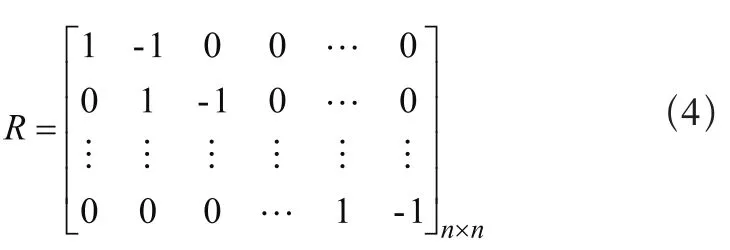
简化计算方程右式后两项在伪距观测条件下可忽略不计，所以令单差观测方程系数为R：

则其单差观测值的方差—协方差阵为：

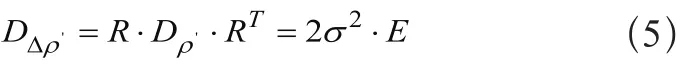
同理由双差观测方程：

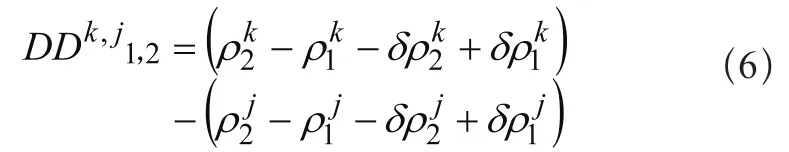
令：

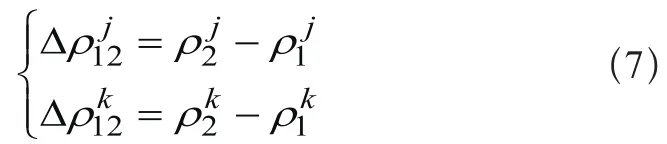
设J为双差观测值系数：

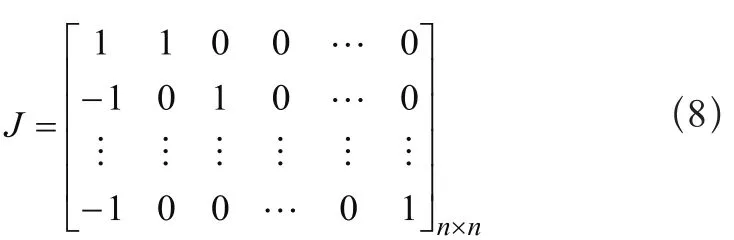
如果一个历元内，两个测站同时观测了n颗卫星时，双差观测量的方差—协方差阵记为：

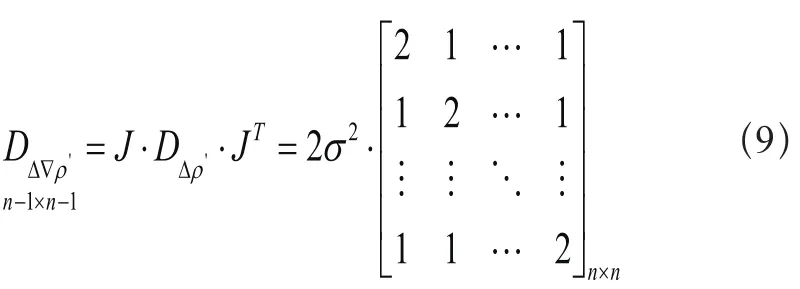
双差观测权阵表示为：

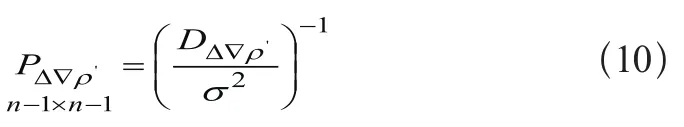
1.2 基于高度角随机模型

即该模型假设观测值精度与卫星高度角之间的相关关系可用某种函数表示。现在比较成熟的基于高度角随机模型有：指数函数模型和三角函数模型等[4]。其中的正弦函数模型和指数函数模型是最近似观测值精度的两种随机模型。本文采用正弦函数与指数函数联合确定随机模型：

（1）在单点非差定位的条件下：设在测站A观测卫星K的高度角记为 ，根据该观测值方差可表示为：

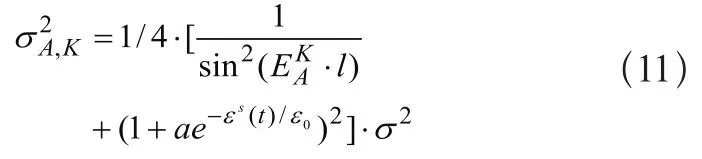
σ为观测值在历元某t时的观测值的中误差，σ0为观测值在接收机天顶方向的中误差，两者的单位均记为米。a为放大因子，εs(t)表示卫星s在历元t时刻的高度角大小，ε0为参考的高度角，两者的单位记为度。

单个测站的卫星观测值的方差阵表示为：

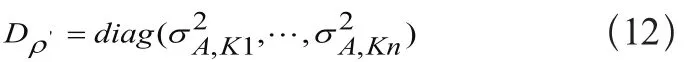
此式即为单点绝对定位中不同卫星的观测值方差阵，所以权阵表示为：

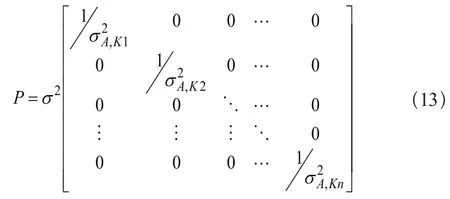
（2）双差相对定位的模式下：两个测站A、B卫星观测量的协方差阵为Dρ'，由前面可知单差虚拟观测值的协方差阵： ，则单差观测量的方差阵表示为：

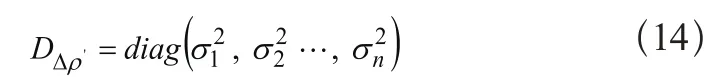
同理双差虚拟观测值方差阵： ，则双差观测量协方差阵可表示为：

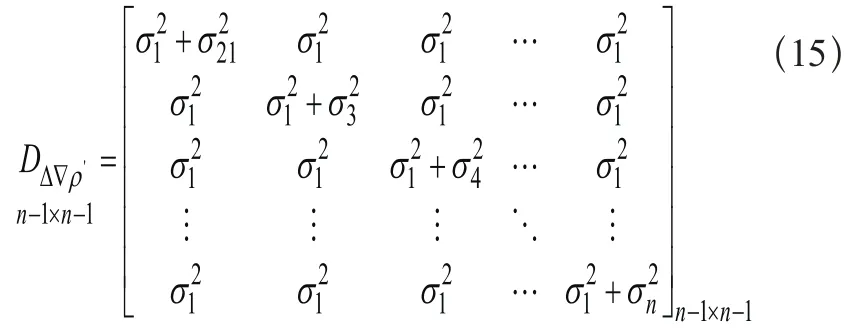
则虚拟观测值权矩阵P为：

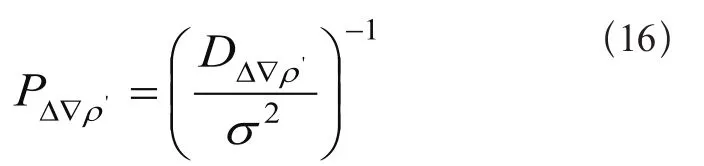
1.3 基于信噪比的随机模型

信噪比(SNR)指的是接收机接收到卫星的载波信号强度与信号噪声强度的比值，常用载噪功率密度比值(C/N0)表示，Ward利用这一性质[1]，建立了利用信噪比计算得到观测值方差的函数模型：

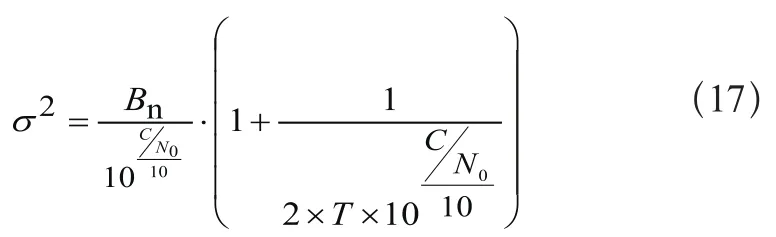
式中：Bn表示载波相位跟踪环的宽度值，T表示一体化检波的时间，其大小约为导航数据的位长，因为观测值噪声的能量量级非常小，可以对其进一步简化得到：

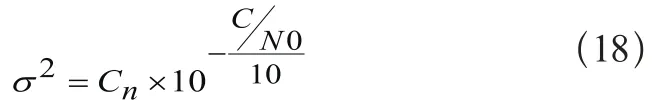
此即为SIGMA-ε模型[2,4]，Cn值的大小主要取决于接收机的跟踪通道得到的相位跟踪环宽度值大小，这里主要采用F.K.Brunner等通过大量试验求得的相对于L1载波的C1值大小为1.61×104mm2来进行下面的试验分析。由误差传播定律得到某一历元双差伪距观测值的方差—协方差关系式，其观测值权阵由 模型确定。

在单点非差绝对定位的条件下单个测站的卫星观测值的方差阵表示为：

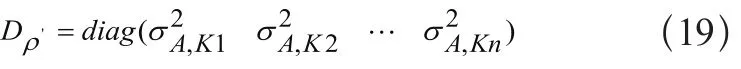
2 算例与分析

2.1 实验数据采集

选取两个测站点A和B架设仪器进行观测，其中测站A和B的近似坐标如表1所示，测站点A使用的是LEICA GRX1200GGPRO 6.00接收机，其天线型号为LEIAX1202G，数据采样间隔为1S。测站点B采用的是LEICA GRX1200GGPRO 6.00 接收机，其天线型号为LEIAX1202G，采样间隔为1S，测站间相距约为2km。

为比较三种随机模型对GPS基线向量解算精度的影响大小，在某地区内选取一条基线，所测得坐标在WGS-84坐标系下。其中，点1处架设的是TRIMBLE NETRS，接收机天线型号为TRM41249.00，采样间隔为1S，共观测了150分钟；点2与点1为同步观测，其观测时段相同，点2处的接收机为TRIMBLE NETRS，接收机天线型号为TRM41249.00，采样间隔同样为1S，具体数据如表1所示。

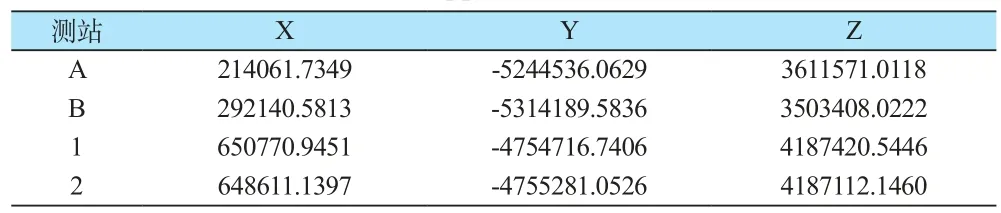
表1 测站近似坐标Table 1 The approximate coordinates

2.2 数据处理结果

（1）单点定位模式下

由单点定位模式下的三种模型比较分析（表2、图1～图3），可以得出：基于高度角的随机模型和基于信噪比的随机模型比等权随机模型定位精度高。所以，在非差单点模式下，可选择高度角随机模型和信噪比随机模型。

在非差单点定位条件下采用高度角随机模型和信噪比随机模型并不是对所有的坐标分量精度都能提高，这就需要根据具体情况选择适合的随机模型进行定位。

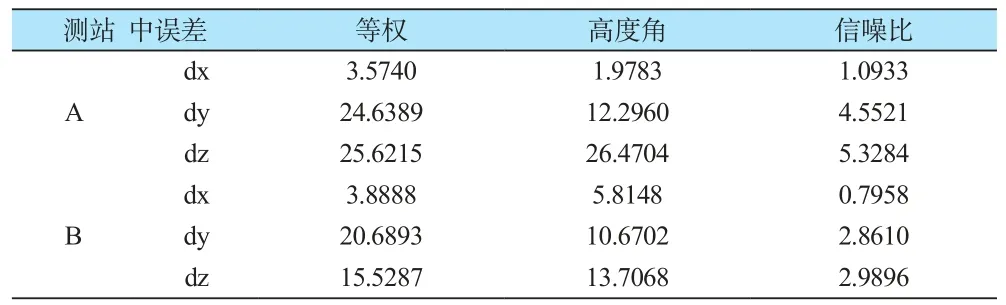
表2 测站中误差Table 2 The middle error

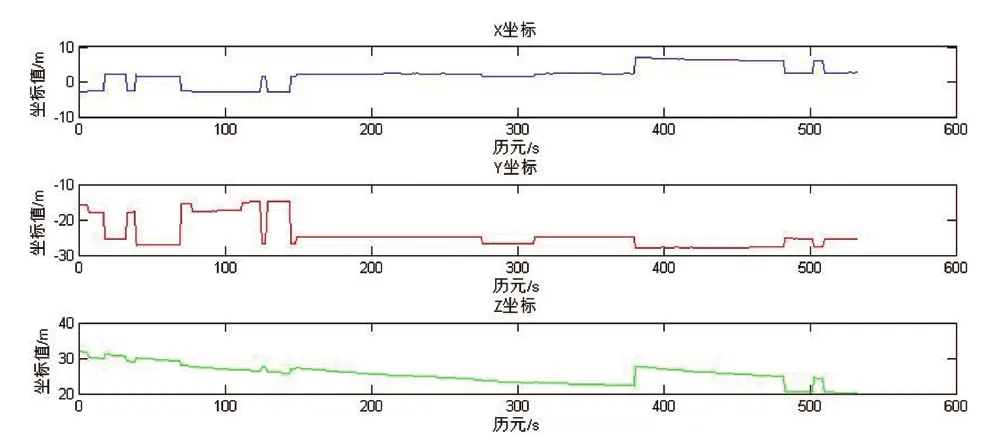
图1 测站A等权模型残差序列Fig.1 The residual error sequence of equal weight model of station A

图2 测站A高度角模型残差序列Fig.2 The residual error sequence of altitude angle model

图3 测站A信噪比模型残差序列Fig.3 The residual error sequence of signal-to-noise ratio model at station A

（2）相对定位模式下

由图表分析可得（表3、图4），在伪距相对定位条件下，高度角随机模型和信噪比随机模型对长基线有略微，这种影响可以忽略不计，而等权模型影响较大，对于短基线的解算，通过实验结果可看出基本上不存在影响。

表3 基线1-2中误差Table 3 The error of base line 1-2

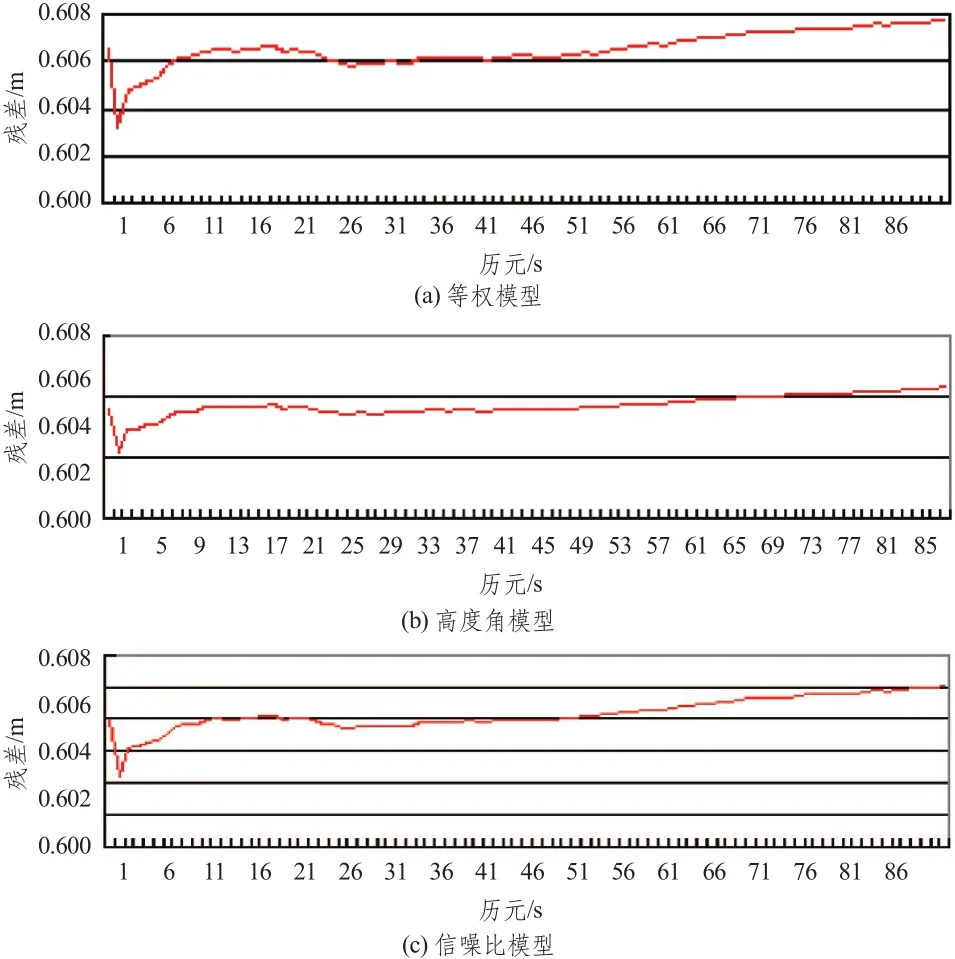
图4 不同模型基线Z方向残差Fig.4 The residual in baseline Z of different models

3 结语

本文以基于伪距观测值的观测方程研究比较了等权随机模型、基于高度角的随机模型和基于信噪比的随机模型。

基于伪距的非差单点定位数据处理中，基于高度角的随机模型和基于信噪比的随机模型比等权随机模型定位精度高；在非差单点定位条件下采用高度角随机模型和信噪比随机模型并不是对所有的坐标分量精度都能提高；在伪距相对定位条件下，高度角随机模型和信噪比随机模型对长基线有略微，这种影响可以忽略不计，对于短基线的解算，通过实验结果可看出基本上不存在影响，实验证明了采用双差相对定位等权模型可以完全满足定位精度的需要。

今后研究实验工作，将增加更多实验组进行实验论证和比较。