启发式路径下节约里程的订单分批算法
王 转,裴泽平
北京科技大学 机械工程学院,北京 100083
1 引言
随着电商B2C业务的兴起与发展,消费者的需求日益多样化、个性化,电商配送中心订单呈现出高频次、小批量的特征。按单拣选的作业模式将大大降低拣货效率,因此在电商配送中心内部多以批量拣选处理客户订单。人到货批量拣选系统是电商物流中心中最普遍的拣货系统,该系统下的拣货时间主要受限于拣货人员在拣货途中的行走距离。因此,如何划分拣货批次以合并订单,使拣货人员行走距离最短成为提升拣货效率的关键。
近年来,关于订单分批策略的研究普遍集中在以不同方法求解分批问题上,例如先到先服务方法、排队理论、种子算法及智能算法等。
先到先服务规则是最为常见的订单优先级别划分方法,依据订单到达系统的时间先后进行合并,在不违反拣选设备容量的前提下,先到达的一批订单首先成为一个批次被拣选出库,因为先到先服务规则较为简单,因此其优化结果也常被用来进行实验对比[1-3]。Lam,Choy,Ho[4]等人借助排队论思想,采用模糊逻辑方法对拣选系统中订单设置优先级并以此为依据进而合并订单,实验结果表明,文中提出的计算方法生成的拣选任务序列使得拣选人员行走距离减少。Ho与Tseng[5]引入巷道指数权重这一概念,提出将巷道编号的指数作为巷道权重,并将完成订单拣选所需经历的巷道权重相加,订单巷道权重最大的订单作为种子订单,利用种子算法对订单合并问题进行求解。在运用智能算法方面,Sören Koch,Gerhard Wäsche[6]提出了一种结合局部搜索过程的分组遗传算法求解订单分批模型。Osman Kulak[7]采用禁忌搜索算法,并通过实验证明该算法在求解订单分批模型时表现效果优于先到先服务分批方法。Borja Menéndez,Eduardo G.Pardo,Antonio Alonso-Ayuso[8]等人提出了一个二阶段的变邻域搜索方法用于求解订单分批模型,并且该方法可以找到一个较好的近优解及若干个保留下来的次优解。Soondo Hong,Youngjoo Kim[9]在考虑历遍式拣选路径的情况下提出了针对宽巷道物理模型的订单分批模型求解方法。实验选取了一个包含六个巷道的拣选系统和一批订单,结果表明采用该方法后的总行走距离比按单拣选缩减少9.9%。此外,Ricardo Pérez-Rodríguez,Arturo Hernández-Aguirre,S.Jöns[10]用分布统计算法求解订单信息未知的在线订单分批问题。
同时,国内学者也热衷于以新方法求解订单分批模型,王旭坪[11]等人采用双目标遗传算法优化人工并行分区的拣选系统,结果表明该方法对小批量订单的分区优化效果较为明显。吴天行,郭键[12]通过构造基于图论的订单合并模型,通过基于图论的合并算法求解模型,但图论方法在求解大规模订单数据时较为困难。马廷伟,雷全胜,李军[13]等人提出了一种利用改进二进制粒子群算法求解订单分批模型的方法以求解小规模订单分批问题。
综上所述,当下国内外学者对于人到货订单拣选系统下的订单分批问题的研究,主要集中于采用不同的方法求解订单分批模型,如优先规则、排队理论、智能算法(启发式算法)等,并由其体现在对求解算法的创新上。然而,智能算法在求解较大规模的订单分批问题时表现效果还有待探索,诸多研究中在算例验证中采用的订单规模数据较小[11-13],无法确定算法是否在较大规模订单数据下依旧表现优越。此外,电商环境下要求订单履行中心尽快处理订单,在较大规模下智能算法是否能够高效的订单分批操作也有待论证,小规模下的分批方法在面对大规模订单数据的条件下很有可能失去造成订单池淤塞瘫痪,进而降低拣选效率。
同时,对于人到货拣选系统来说,能够提供标准化的作业模式是重要的考虑因素,采用智能算法优化算法后生成的批量拣货单行走路径复杂多变,不易拣货人员记忆,可行性差[14]。如果能在传统的拣货策略上研究较为可行的启发式拣货策略,将会对人到货拣选过程的作业效率、服务水平以及降低物流成本具有重要价值。
因此,本文综合考虑拣货器具容积和商品包装体积多样化因素,以批次拣选单距离节约量最大化为目标,构建基于里程节约的订单分批模型。结合启发式路径策略,构造距离节约量函数以合并订单,提出基于订单间节约里程量的订单分批算法。最后将本文提出的D-eco算法(基于启发式路径下里程节约的订单分批算法)与目前广泛使用的FCFS方法(先到先服务方法)、SBBM方法(基于订单相似度分批方法)进行性能分析对比,以探讨D-eco算法在求解订单分批问题时的优势。
2 基于里程节约的订单分批模型
2.1 问题描述
采用订单合并的批量拣选策略可减少总的行走距离,提高拣选效率。通常情况下,订单合并是将一组订单集合分批为几个小的订单子集合,每个批次由一个拣选员工进行拣选。值得注意的是,每个合并批次都不能超过其拣选设备的容量,若超过容量,则应将超出部分的订单分配到其他合并批次中。总的来说,订单合并问题就是在拣选路径策略、拣选设备、商品位置等信息已知的情况下,如何将一组订单集合分为数组订单批次,以最小化所有订单批次的行走距离。
图1至图3证明了两订单合并拣选比分别进行拣选所行走的距离有所减少。图1和图2分别表示完成订单1和订单2在仓库中需行走的路径,假设订单中所包含的商品在拣选货架上的分布已知,且采用遍历型拣选路径策略。图3则为订单和合并后的行走路径,从图中可以看出合并后的路径长度明显要比单独进行拣选所行走的距离短。订单合并问题的特征与带容量约束的车辆路径问题相似,都是对客户或商品访问顺序的优化。但不同的是,订单合并问题需保持订单的完整性,每个订单的商品都必须在同一次拣选过程中完成,不得拆分。因此传统的车辆路径问题解决办法无法应用到订单合并问题上。

图1 订单1拣选路径

图2 订单2拣选路径

图3 订单1与订单2合并后拣选路径
2.2 模型假设
本文研究的对象是人到货的订单拣选系统,采用订单合并策略来提高拣选作业效率。拣选区域布局如图4所示,拣选区域中摆放若干组多层货架,货架中摆放不同的商品,假设货架大小宽度相同,且每种商品能存放在货架一处。拣选人员拿到拣选任务单后,依据订单中商品位置和数量等信息开始拣选工作。员工驾驶叉车从入口出进入货架间通道,依据事先规定好的拣选路径策略在通道中行走,拣取任务单中的商品,并放置在叉车托盘中,当拣选完任务单中的所有商品后,员工回到入口等待接收下一批次的拣选任务。

图4 拣选系统布置
本文研究对象为人到货的整箱拣选系统,该系统采用P-C储运模式,即以托盘(P)为单位存储,以箱(C)为单位拣选,系统模型假设条件如下:
(1)拣选货架为托盘货架,一层用于拣选,二层以上用于存储。
(2)货架一层每个货位为一个拣选点,每个拣选点唯一对应一个商品品规。
(3)采用托盘或笼车作为拣选器具,每次拣选可完成多个订单的拣选(批量拣选)。
(4)每个订单所订商品的总体积不超过拣选器具的装载体积。
(5)订单不允许分割,即一个订单只能分配给一个拣货任务。
2.3 模型建立
以往研究者求解的传统订单分批模型[15]以分批后拣选距离最短为目标,在模型求解阶段时还需考虑订单合并依据(例如按订单相似度合并),本文建立的订单分批模型以批次拣选单距离节约量最大化为目标,配合距离节约函数,相比以往订单分批模型更易求解。同时,以往订单合并模型将全部商品体积视为相同的,均为“1”单位体积,本文引入商品堆码数的概念,增加了对不同商品体积的考虑。
建立基于节约里程且考虑商品包装体积的订单分批模型,首先对模型中变量与常量做以下定义:
I:表示订单集合,i∈I;
K:表示批次任务单集合,k∈K;
J:表示商品品规集合,j∈J;
Vmax:表示拣选设备最大容量;
qij:表示订单i中品规 j的商品数量;
cj:表示订单i中品规 j的商品堆码数;

目标函数(1)表示订单分批后,批次里程节约量之和最大;约束(2)为拣选设备装载体积约束,表示每个批次商品总体积不超过拣选设备最大装载体积;约束(3)表示一张订单只能分配到一个批次任务中。该模型的解为向量Yk=(Y1k,Y2k,…,Ynk),即第k个批次任务单的订单组成。
3 基于里程节约的订单分批算法
研究表明,订单分批模型的求解属于NP-hard难题[15]。且求解上述基于里程节约的订单分批模型还需考虑路径策略、商品包装体积等因素,因此在面对大规模数据时求解难度较大,本章提出一种基于启发式路径策略下里程节约量的订单分批算法对模型进行求解。
3.1 距离节约函数


图5 “S&U”启发式拣选路径
3.2 “S&U”启发式路径里程算法
图5为“S&U”型启发式路径策略,相比图6中的历遍式拣选路径策略和返回式拣选路径策略,“S&U”型路径能够有效减少拣货行走距离。
在编写拣货路径里程算法前,需对拣选区域特征参数进行定义,首先对拣货任务单中各待拣巷道进行编号:例如某一拣货单中涉及到3条待拣巷道,则按从左到右的顺序3条待拣巷道的编号为A1、A2、A3,第i条待拣巷道编号为Ai,此外对算法流程中出现符号做如下介绍,符号示例如图7所示。
P0:拣货人员起点;

图6 历遍式拣选路径与返回式拣选路径

图7 拣货路径算法参数示例
Tup:拣选区域上方通道;
Tdown:拣选区域下发通道;
Aleft:拣货人员出发后距离其最近的待拣巷道;
Alast:拣货任务单中最后一条待拣巷道;
L:巷道长度。
“S&U”型启发式路径里程算法流程如图8所示,算法规则如下:

图8 “S&U”型拣选路径算法流程
(1)若巷道中所有待拣商品的位置距巷道入口的距离均小于巷道总长的1/2,则拣货人员完成拣货后折返至原通道并行走至下一条待拣巷道。
(2)若巷道中存在某待拣商品且其储位距巷道入口的距离大于巷道总长1/2,拣货人员并完成拣选并穿越巷道后到达仓库另一端通道,行走至下一条待拣巷道。
(3)若巷道中不存在待拣商品,拣货人员跳过该巷道行走至下一条待拣巷道。
(4)多次运用规则(1)~(3)至拣货结束,并输出拣货人员行走总距离。
3.3 基于节约里程的启发式订单分批算法
在构造距离节约函数和确定拣货路径后,本文基于节约里程的改进式种子算法对订单进行分批。该算法从全局角度入手,在不超过拣选设备容量的前提下,计算两两订单的最大距离节约量,每次合并时均选取节约量最大的两个订单合并,直至订单分批完成,算法流程如图9所示。该算法主要步骤如下:
步骤1计算距离节约量。若订单集合I中存在多个订单,则计算各订单间的距离节约;否则,执行步骤6。
步骤2订单选择。选择距离节约量最大的订单Im与In,订单商品总体积分别为Vm与Vn。
步骤3合并订单,判断订单容量是否满足拣选设备体积约束。
若Vm+Vn≤Vmax,合并 {Im,In}后将{Im,In}加入I,并删除Im与In,返回步骤1。
若Vm+Vn>Vmax,违反体积约束,执行下一步。
步骤4选择其余订单合并。选择Im与In中订货量更大的订单(如Im),计算Im与其余订单间的距离节约量。如果存在Il与订单Im的距离节约量较大,且满足Vm+Vl≤Vmax,则合并{Im,In}并删除Im与Il,返回步骤1;否则,执行下一步。
步骤5直接生成拣选任务单。如果没有订单在满足体积约束的情况下能合并Im,则Im直接生成拣选批次单,删除I中的Im,返回步骤1。
步骤6 I中仅剩1张订单,则其单独成为一个批次拣货任务单。
步骤7结束。
4 仿真分析与比较
基于MATLAB R2015a开发环境,设计不同订单池规模的实验方案,对前文提出的基于里程节约的订单分批优化模型及算法进行仿真验证。选取合适的评价指标,通过同FCFS、SBBM两种方法的实验对比,论证本文提出的D-eco分批算法在不同订单规模下的有效性。

图9 基于里程节约的订单分批算法流程
4.1 参数设置
(1)拣选区域参数
实验搭载的物理模型如图10所示,其中托盘货架一层用于拣货作业,上层用于存储,每个拣选点对应一种商品;拣选货位尺寸与实际托盘式货架相匹配;考虑到拣选设备作业空间面积,实验中巷道宽度与实际托盘货架拣选区中巷道尺寸相符;实际物流中心内部存储品规较多,其中部分品规出库次数频繁,故往往对该类商品加以管理,专门设置拣选区以方便商品出库,本仿真实验设计的拣选区货架共计10排8列,拣选点共计80个,拣货人员从起点开始,沿巷道中心线行走,同时向左右两边拣货。拣选区域详细参数如表1所示。
(2)订单池数据

图10 实验拣选系统布置

表1 拣选区域参数
实验选取数据为某电商物流中心的真实订单,鉴于一天中各时段下订单处理系统的订单池容量不同,因此本文设计选取5个容量不同的订单池以代表不同规模的订单数据进行实例验证。订单主要参数是通过EIQ数据分析后得到的订单特征值:EN表示每张订单的行数,EQ表示每张订单的订货量,EIQ表示每张订单每行订货量,实验订单池特征如表2所示。

表2 实验订单池参数
(3)评价指标
为衡量各订单分批方法表现效果优劣,本文选取两个指标对算法表现进行评价:
①拣货总距离S:完成所有拣货任务所行走的总距离,总行走距离是评价拣货效率高低的直接标准,有效的分批方法可以减少路线迂回,大大减少拣货距离。
②平均行走距离SK:完成每个拣货任务单所走的距离,包含拣货总距离和拣选任务单数量两个维度,能够更好地衡量拣选批次任务单的工作强度。
4.2 实验方案
为研究本文所提出的D-eco分批算法的有效性,本文分别对FCFS、SBBM以及D-eco分批算法进行仿真程序设计,并生成拣货路线图用以指导拣货人员按生成的批次拣选单及拣货路径进行作业。
FCFS算法由于其简单性、快速性而被广泛应用于现实生活中,FCFS方法的原理为按订单到达时间顺序排序后分批,直至不满足拣选设备装载体积约束时即形成一个批次。
SBBM算法包含两个阶段:第一阶段选择种子订单,第二阶段进行订单合并。在订单合并阶段,首先选出的种子订单作为订单合并批次的初始订单,再按照一定的标准将剩余的订单加入到种子订单中,SBBM算法以相同通道系数Simimn作为订单间相似度的度量方式,即两订单相同待拣巷道数与两订单全部待拣巷道数的比值:

4.3 结果分析
三种分批方法的仿真实验结果如表3与表4所示。其中表3为不同订单池容量下三种方法输出的拣货任务单数K,表4为不同订单池下三种方法输出的总行走距离S和平均行走距离SK。

表3 不同订单池下拣选批次数

表4 不同订单池下平均行走距离和总行走距离
由表3中输出的拣货任务单结果可以看出,同一订单池下,三种算法所得到的拣货任务单数量K相差很小。分析可得,拣货任务单数K受拣选设备装载体积影响最大,其他因素对其影响很小。因此选择其作为评价指标并不合适,本文仅用该输出结果计算平均行走距离SK。
表4中的实验结果表明,在各容量订单池下,D-eco算法下的总行走距离最短,且实验结果明显优于FCFS算法;尽管在订单规模较小(订单池容量≤100)时,D-eco与SBBM算法所得的总行走距离S相差不大,但随着订单池容量增大,D-eco算法有效性愈发凸显,当订单池容量为250单时,D-eco算法下的总行走距离仅为1 983 m,其优化后拣货总距离比FCFS多缩减了12.2%,比SBBM多缩减了2.1%。并且由图11中的曲线斜率可以推断:相比其他两种算法,随着订单池规模增大,采用D-eco算法所节约的距离将更多。

图11 三种算法下总行走距离S对比曲线
图12 为三种算法下各拣货任务单平均行走距离SK的对比图。实验结果表明,在各容量订单池下D-eco的表现效果均优于FCFS和SBBM。由于FCFS忽略订单间联系,因此该算法下的拣货任务单下的拣货路径将会有较多迂回,平均行走距离SK近乎于D-eco算法所得结果的2倍。SK同时包含拣货总距离与批次任务单数量两个维度,能够更好地评价算法的有效性,因此说明本文提出的D-eco在各种订单规模下的分批优化效果更好。
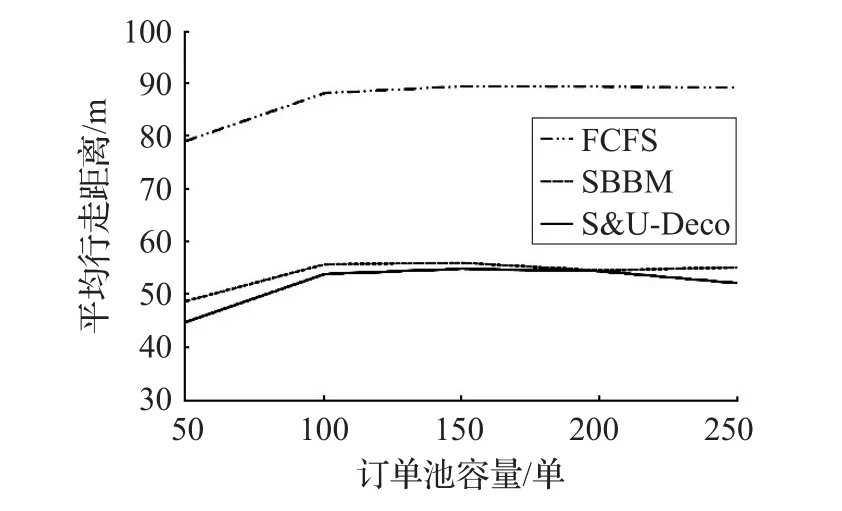
图12 三种算法下平均行走距离Sk对比曲线
综上所述,可得以下结论:
(1)D-eco所得的总行走距离S最短,且随订单数增加,其优化效果愈发明显。
(2)D-eco所得的平均行走距离SK最短,拣货人员完成D-eco生成的任务拣选单时将更迅速。
(3)三种算法中,随着订单规模的增大,D-eco能够比FCFS和SBBM节约更多的行走距离。

图13 某一拣货任务单拣货路径图
此外,为更好地指导拣货人员持拣货任务单进行拣货,应对拣货人员做出正确的路径引导。图13为仿真实验生成的动态拣货路线图(该图实际上为动态图,拣货顺序和路线是动态可视的),拣货人员需要拣选的货位被标记在图中,且拣货人员行走路线符合“S&U”启发式路径策略,拣货路径图的生成可以有效避免拣货人员发生路线错误的情况,与仅显示分批结果的单据相比,结合路径动态图的拣选任务单更适合于实际拣货作业。
5 结束语
本文首先构建基于节约里程的订单分批模型,模型中首次新增了商品堆码数这一参数,将商品包装体积多样化纳入考虑;采用“S&U”型启发式路径策略,并设计“S&U”型启发式路径算法以计算拣选订单里程;构造距离节约函数计算订单间里程节约量作为订单合并依据;设计基于节约里程的订单分批启发式算法进行订单合并;最后,在不同订单池容量下对FCFS、SBBM、D-eco三种订单分批方法进行仿真实验。结果表明,D-eco算法表现效果最好,能够有效减少拣货行走总距离和平均行走距离。在5种不同订单池容量下,采用D-eco算法进行分批优化后的拣货总距离平均比FCFS多缩减了12.2%,比SBBM多缩减了2.1%。
综上所述,本研究从物流中心存在的实际操作问题出发,综合考虑不同商品体积、拣选设备装载体积等条件和约束,提出了一套有效的订单分批方法。该方法丰富了订单分批算法,计算效率高,优化效果明显,对于电商配送中心人到货的拣选具有较高的应用价值。同时,该方法下的拣货路径更适合应用到实际拣选作业中,可为企业物流中心的运作管理提供决策支持。另外,本文的研究成果同样可以应用到人到货的零拣系统中。

