基于低秩稀疏分解的自适应运动目标检测算法

朱 林，郝元宏，蒋秀蓉

北方自动控制技术研究所，太原 030000

1 引言

运动目标检测是许多计算机视觉应用的第一步，例如交通监控、机器人导航、增强现实等[1]。运动目标检测的任务就是把被称为“前景”的运动目标区域从被称为“背景”的场景中分离出来，为目标识别、目标跟踪、目标行为分析提供可靠而准确的数据[2]。因此，运动目标检测是计算机应用中十分关键的一步。

常见的运动目标检测算法有差分法、光流法、背景减除法等。其中背景减除法是最主要的一类方法。在此类方法中，背景通常被假设是静止的，通过比较当前图像与背景模型的不同来得到前景。在过去的几十年内，国内外学者们建立了一系列的背景建模方法，包括单高斯模型[3]、混合高斯模型[4]、非参数核模型[5]、隐马尔科夫模型[6]、线性回归模型[7]、ViBe背景减除[8]方法等。然而，实际场景下的运动目标检测问题，往往受到背景杂波、噪声、光照变化、场景中存在的阴影等因素的影响，现有的运动目标检测算法难以处理各种复杂的场景[9]。

近几年，鲁棒主成分分析理论（Robust Principle Component Analysis，RPCA）[10-11]出现，其在运动目标检测领域受到了越来越多的关注。其核心思想在于在摄像头静止的条件下，将各视频帧作为列向量依次排列形成视频矩阵，由于视频矩阵中的背景一般变化不大，所以背景应具有低秩特性；前景目标一般占整个图像的一小部分，其具有稀疏性且不具有低秩性，具有离群值的特征。此种方法可以把视频图像分解为低秩背景和稀疏前景，与传统方法相比在算法的准确性和鲁棒性上具有十分明显的优势。与先前的背景建模方法相比，低秩模型能够对噪声、数据缺失、缓慢的光照变化等退化因素保持鲁棒，对于前景目标的运动方式无特殊要求，能够处理非刚体对象，并且需要调节的参数较少。经过一系列的实验验证，鲁棒PCA模型取得了较好的静态背景建模效果，这为RPCA模型在运动目标检测问题中的应用奠定了良好的基础。

然而，在实际应用中RPCA仍然有一些不足。首先，RPCA模型使用l1范数来约束矩阵元素的稀疏性，l1范数并未考虑矩阵元素之间内在的空间相关联系。在处理复杂的场景时，传统RPCA模型的性能会受到极大影响。实际上，前景目标的像素之间往往是空间连续的。如果能把此先验知识引入到RPCA模型中，其准确性和鲁棒性会大大提高。其次，由于RPCA模型对参数十分敏感，并且没有一个参数可以很好地处理所有场景，因此其正则化参数λ的选取是十分困难的。

为解决以上问题，本文提出了一种新的运动目标检测算法。通过把空间融合稀疏约束引入到RPCA模型中，约束了前景模型的稀疏性和空间连续性；同时，为了解决正则化参数的选取问题，本文设计了一种自适应参数估计方法。最后，在低秩稀疏分解的框架下，使用基于交替迭代思想的增广拉格朗日乘子法对新的目标函数进行求解，得到稀疏前景矩阵。在公共数据集上的大量实验证明，在处理动态背景等复杂环境时，本文算法的鲁棒性和准确性有很大提高。

2 相关知识

希望结合低秩系数分解与Fused lasso模型，找到一种鲁棒性和准确性更强的运动目标检测算法。因此，首先给出低秩稀疏分解和Fused lasso模型的介绍。

2.1 低秩稀疏分解

低秩稀疏方法在计算机视觉中有着很广泛的应用。其最经典的方法是RPCA方法，受低秩矩阵分析的相关研究启发，文献[10]提出通过主元追求（Principal Component Pursuit，PCP）求解RPCA问题，其核心思想在于将视频矩阵分解为一个低秩矩阵和一个稀疏矩阵。

矩阵D对应观测矩阵；矩阵E对应于分解后矩阵的稀疏部分，即视频数据中的目标部分；矩阵A对应于分解后矩阵的低秩部分，其表示原始观测数据中恢复出来的低秩数据部分，即背景部分。根据背景矩阵A与前景矩阵E分别具有低秩与稀疏的特性，可以将视频矩阵分解成为低秩矩阵和稀疏矩阵两部分，其具体原理如下：

式中，‖A‖*为矩阵A的核范数，即矩阵所有奇异值之和；‖E‖1为矩阵E的l1范数，即矩阵所有元素绝对值之和。通过求解此模型，可以分解出低秩背景矩阵A和稀疏前景矩阵E。

但在实际应用中，视频序列图像本身包含动态背景（如树叶晃动、水面波纹等），在时空域分布上呈现为类似噪声特性，l1范数往往不能对前景目标很好地建模。考虑到前景目标具有很强的空间相关性，即使视频图像受到噪声影响或动态背景的干扰，前景目标区域内的相近像素之间的灰度值也通常不会有很大变化，其整体呈现线性关系。因此希望利用前景目标的空间连续性先验信息对前景目标进行建模，结合矩阵低秩稀疏分解框架，提出一种鲁棒性和准确性更强的运动目标检测算法。

2.2 Fused lasso模型

Lasso[12]（Least absolute shrinkage and selection operator）将l1范数作为惩罚项加入最小二乘回归，l1范数惩罚项对向量中所有元素的绝对值和进行惩罚，其产生的结果一定是稀疏的。传统RPCA方法的稀疏矩阵就是通过求解LASSO问题得到的：

LASSO模型只能诱导元素的稀疏性，为了同时诱导元素的稀疏性和元素之间差异的稀疏性，R.Tibshirani等人提出了Fused LASSO 模型[13]：

式中，第一个约束项可以约束元素的稀疏性，第二个约束项可以约束元素之间的平滑性。因此，Fused LASSO模型可以使元素在稀疏化的基础上产生分段的平滑性，可以有效地去除数据中的噪声及数据缺失等情况。在实际运动目标检测应用中，Fused lasso能够比lasso取得更好的效果。

3 基于低秩稀疏分解的运动目标检测

传统的RPCA方法使用l1范数对前景进行建模，在实际应用中并不能有效地区分目标和动态背景。为了提升检测的准确性，本文结合空间先验知识和稀疏先验知识，对前景模型进行建模，定义了空间融合稀疏约束如下（Spatial fused sparse constraint）：

式中，D(⋅)表示在矩阵空间邻域上的差分操作，c是平衡空间平滑约束和稀疏约束强度的正则化系数。诱导矩阵X中元素的稀疏性，诱导矩阵X中元素的空间平滑度。

假设待检测视频序列为M∈ℝm×n×p，其中m、n分别是每帧图像的长和宽，p是视频序列的帧数。把每一帧拉伸成一个列向量，得到观测矩阵D∈ℝmn×p。通过把空间融合稀疏约束引入到低秩稀疏分解模型中，得到待解决的目标式：

式（7）可以通过增广拉格朗日乘子法[14]进行求解。其增广拉格朗日方程为：

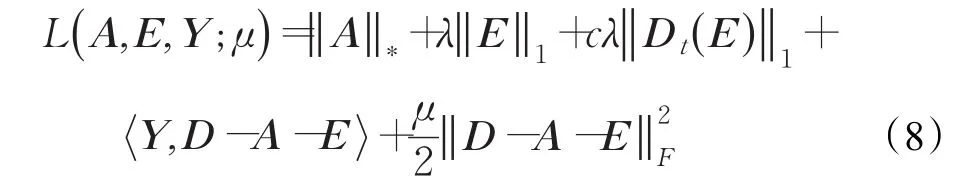
式中，Y是拉格朗日乘子，μ是惩罚参数。为保证求解过程的效率和准确性，采用交替方向法求解式（8）。

3.1 低秩背景矩阵估计

首先，固定前景矩阵E，低秩背景矩阵A可以通过优化下式求解：

式（9）可以表示为如下形式：

式（10）可以通过软阈值收缩算法[15]求解。下面介绍引理1。

引理1给定一个矩阵W∈Rmn×p，矩阵W 的奇异值分解为，则奇异值收缩算子定义为：

式中：

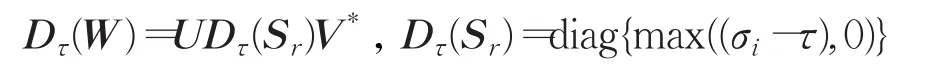
运用引理1，可以求得式（10）的最优解：

3.2 稀疏前景矩阵估计

对于稀疏前景矩阵估计问题，可以通过最优化下式解决：

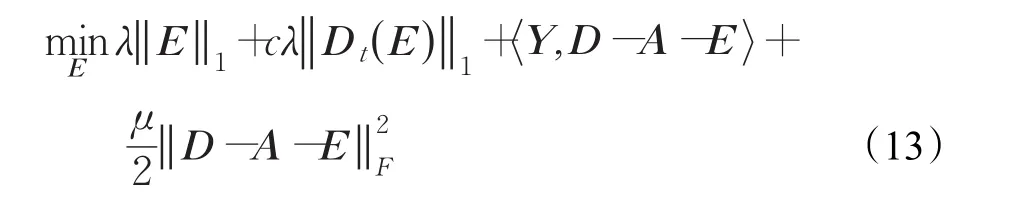
式（13）可以转化为如下形式：

设Q=D-Ak+1+μ-1Yk，则式（14）可以转化为：

式（15）的形式与式（5）中的Fused lasso问题相似，可以通过SLEP package[16]快速求解。

3.3 自适应参数更新策略

当算法框架搭建完成后，如何选择合适的参数是一个重要的问题。参数λ控制着空间融合稀疏约束的强度，即对前景矩阵空间连续性和稀疏性的约束；参数c用来平衡空间连续性约束和稀疏性约束的强度。文献[17]提出了一种在线性回归模型中的参数估计方法，受此启发，设计了一种自适应参数更新策略以提升算法的鲁棒性。

本文算法中参数λ的选择问题与基追踪去噪问题类似[18]。受此启发，首先根据实验经验把λ的值设置为，其中M对应于观测矩阵中元素的数量，σ是需要估计的尺度参数。同时考虑算法的计算复杂度和自适应性能，选用了一种基于绝对中位差的策略来估计σ：

式中，K是用来完善λ的一个常量。在本文的实验中，K的值被设置为2。

3.4 基于低秩稀疏分解的自适应运动目标检测算法

本文算法步骤如下：

输入：观测矩阵D

输出：前景位置矩阵E

步骤1初始化：A=E=0，Y=0

步骤2交替迭代求解矩阵A和E

步骤2.1通过式（10）～（13）估计背景矩阵A。

步骤2.2 通过式（16）～（17）计算正则化参数 λ。

步骤2.3通过式（13）～（15）估计前景位置矩阵E。

步骤2.4检查是否符合算法收敛条件：

若符合，停止迭代。

步骤3输出结果。

整个算法流程如上所示，在本文实验中迭代停止阈值ε被设为10-7，ALM参数被设为ρ=1.5。关于ALM算法求解的更多细节请参考文献[14]。

4 实验结果与分析

在本章，为了证明本文算法的有效性，将本文算法与7种常用的算法比较，分别是DECOLOR[19]，PCP[10]，VBRPCA[20]，PRMF[21]，MoG-RPCA[22]，ViBe[8]和 MoG[4]。其中，前五种算法是近几年提出的基于低秩稀疏分解的算法，后两种算法是工程实践中常用的有效算法。为了公平比较，所有的算法参数都以原作者给出的最佳参数设置。实验视频均来自于公共数据集I2R dataset[23]，CDnet dataset[24]和 UCSD dataset[25]。在实验中，选取每段视频中带有前景目标的48帧图片，并以最后一帧的检测结果作为比较。

图1使用了来自I2R数据集的7个视频序列进行测试。I2R数据集包含一系列具有动态背景和静止背景的视频序列，它常被用作前景背景分离问题的基准数据集。“Boostrap”“Hall”“Lobby”和“Shopping Mall”描述了具有地面反光的室内拥挤场景。从检测结果可以看出，本文算法可以消除大部分的阴影；由于引入了马尔科夫随机场，DECOLOR方法倾向于提取大的前景区域，其检测结果无法消除阴影；VBRPCA、PRMF和MoGRPCA是基于概率的RPCA方法，其仍然不能完整去除阴影；ViBe检测出的前景目标不够完整；PCP和MoG则产生了大量虚警。视频序列“Escalator”“Fountain”和“Water Surface”是具有动态背景的场景。只有本文算法和DECOLOR方法可以消除动态背景的影响，但DECOLOR方法会使多个相近的目标连成一起，从而产生大量虚警；本文算法能够在消除动态背景影响的基础上检测出准确的前景。另外，对于目标缓慢移动的情形（water surface），只有本文算法可以检测出准确的前景目标。

为了进一步证明算法的优越性，从CDnet和UCSD数据集中选择了5个具有较大动态背景的视频序列进行实验，这些视频序列比I2R数据集更具有挑战性。如图2所示，视频序列“Birds”描述了海鸟在海岸边走过，具有十分剧烈的动态背景。不难看出，只有本文算法检测出了准确前景，其他七种算法均不能处理此种情况。在视频序列“Bottle”的检测结果中，同样只有本文算法取得了较好的效果；ViBe算法虽然消除了动态背景的影响，但也丢失了大量前景像素；DECOLOR算法的检测结果则在前景目标周围检测出了大片的错误区域；其他几种算法均不能消除水波影响。对于视频序列“Boats”“Rain”和“Fall”，相比其他几种算法，本文算法能够在彻底消除动态背景的情况下检测出较为准确的前景区域，取得了较好的效果。

图1 I2R dataset检测结果

图2 CDnet dataset和UCSD dataset检测结果

表1 图1和图2中检测结果的F-measure值（最高值：加粗，次高值：下划线）

为了定量评估算法结果，使用召回率（recall）和准确率（precision）评估前景检测的准确性：

式中，TP，FP，FN分别表示真实正样本，错误正样本和错误负样本。TP可以通过计算被正确检测出的前景像素的数量得到，FP可以通过计算背景像素被错误检测为前景像素的数量得到，FN指前景像素被错误检测为背景像素的数量。

为了同时衡量召回率和准确率，使用F-measure对检测结果进行评估：

如表1所示，本文算法在大部分视频序列中取得了最高或者次高的F-measure值，并且得到了最高的平均F-measure值。相比其他算法，本文算法在每个视频序列中均取得了最高的准确率。对于一些室内拥挤场景（如Bootstrap、Shopping Hall），本文算法未取得最高的F-measure值，这是因为由于空间融合稀疏约束的引入，一些趋于静止的目标会被消除掉，从而降低了召回率。DECOLOR方法的平均F-measure值仅次于本文算法，其检测结果在大部分序列中取得了值最高的召回率，但是由于该方法会产生大量虚警，其准确率会相对较低。其他六种算法在个别视频序列中有较好的表现，但综合表现均不如本文算法。

本文算法代码使用Matlab编写，在台式计算机上运行，配置为3.6 GHz Inter i7 CPU及4 GB RAM。由于RPCA相关的方法是批处理的算法，为了对RPCA相关的方法进行运行效率对比，本文使用100帧图像来对算法进行测试：在分辨率为320×240的情况下，本文算法需要182 s，DEC需要176 s，PCP为197 s，VBRPCA为72 s，PRMF 为 69 s，MoG-RPCA 为 83 s；在分辨率为160×120的情况下，算法运算时间分别为42 s，19 s，32 s，18 s，15 s，22 s。

5 结论

RPCA方法被广泛应用于目标检测应用中，但是仍有一些问题需解决。为提高算法的鲁棒性和准确性，本文提出了一种基于低秩稀疏分解的运动目标检测算法。首先，使用空间融合范数对前景像素的空间连续性和稀疏性进行约束，使前景模型更符合实际情况。其次，提出了一种自适应参数更新策略，使算法的鲁棒性更强。大量实验证明，相比传统方法，本文算法的性能有很大提高。特别是在处理动态背景等复杂环境时，本文算法的鲁棒性和准确性均比传统方法优越。