基于图像对比的PS考试主观题评阅方法

李志磊，程永强，贾昊丽

太原理工大学 信息与计算机学院，太原 030024

Photoshop（以下简称PS）软件是目前著名的图像处理工具之一，功能强大，在诸多行业均有应用。传统的PS阅卷系统已实现客观题的自动评阅，但是主观题仍是由人工评阅。设计一套可以实现主观题自动评阅的PS技能考核系统非常有意义。在现有研究中，文献[1-2]通过分析PSD文档结构，提取文档的基本信息，并将其转换成XML格式文档，通过对考生操作步骤进行量化分析来评阅所得分数。但该方法并没有提取图层画面的细节信息，无法评判考生图像的实际处理效果。卷积神经网络在图像对比分类方面表现优秀，但是在考试前并不能得到足够的样本来进行网络的有效训练。

在PS考试中，考试原图与标准答案图及考生答案图三图可能非常相似，仅对比考生答案图和标准答案图难以对考生层次进行有效划分。且由于考题为主观题，每次考试考官出题时难易程度难以做到一致，仅比较两图的相似度并不能衡量考生在原图的基础上为增大与标准答案图的相似度而做出的相对工作量。例如在两次考试中考生图与标准答案图的相似度都为90%，但是第一次考试中原图与标准答案图的相似度为80%，而第二次考试中原图与标准答案图的相似度为10%，仅比较两图的相似度两次考试都给90分这显然有失考试的公平性。如何做到精准度量考生操作对增大原图到标准答案图相似度的贡献是PS主观题阅卷的关键。本文采用图像相似度对比的方法，通过提取三幅图像（原图，标准答案图，考生图）的颜色，边缘，纹理特征，进行两两相似度度量[3-9]，运用本文所提出的基于三角形的欧氏距离归一化算法得出图片之间的相似度，然后给出考生所得分数。

1 图像颜色，边缘，纹理特征的提取

直方图算法计算简单，具有旋转不变性[10]，且便于计算欧氏距离。本文经过特征提取后把图像的的颜色，边缘，纹理特征分别统计为颜色，边缘，纹理直方图。

1.1 图像的颜色特征提取

由于图像的非平滑区比平滑区所含的信息量更大，因此在进行量化编码时本文对非平滑区进行了更加精细的划分，颜色特征提取采用文献[11]所提出的方案。文献[11]在计算块梯度时仅仅考虑了垂直和水平方向，本文对其进行了改进，在计算时加入45°和135°方向的梯度计算。具体算法如下：

（1）将原始图像分割成相邻但不重叠的4×4大小的子块。

（2）计算每一子块的区域梯度值Grad(I)。

（3）根据区域梯度值的大小，将图像划分为均匀区域和非均于区域。

（4）若是均匀区域，则在RGB空间对图像进行均匀量化；若是非均匀区域，则在HSV空间对图像进行非均匀量化。

（5）直方图统计索引编码。

1.1.1 区域梯度的定义与划分

子块划分如图1。

图1 子块划分

令：

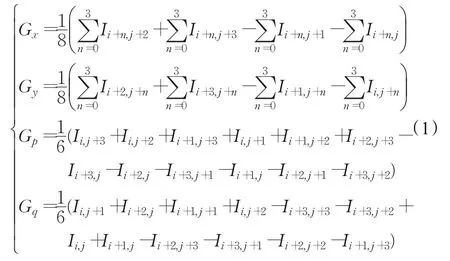
块梯度Grad定义如下：

Grad(I)的值越大，则说明该颜色块区域越活跃，反应在图像中是边缘部分。反之则说明该区域块颜色变化不明显，在图像中为背景部分。设定一个合适的阈值，本文设定为16，当Grad(I)的值大于16时，将该区域块划分为颜色非均匀区域，反之则将其划分为颜色均匀区域。

1.1.2 图像不同区域的颜色量化

由于颜色均匀区域对人眼的视觉冲击小，所含信息量较少，因此对其进行了步长较长的均匀量化。选取对应子块中原16个像素点的RGB值所对应灰度值的平均值为该子块的像素值，然后将其均匀量化到32阶。然后分别统计32种灰度级所对应的像素点的数目，得出图像均匀区域的均匀量化32维灰度直方图。其中RGB值转化为灰度值的心理学公示如下：

颜色非均匀区域对人眼的视觉冲击力大[12]，在此对其进行了更加精细的非均匀量化。在量化编码时采用了更符合人眼视觉观察系统的HSV颜色空间。选用了文献[13]的非均匀量化方案，量化公式如下：

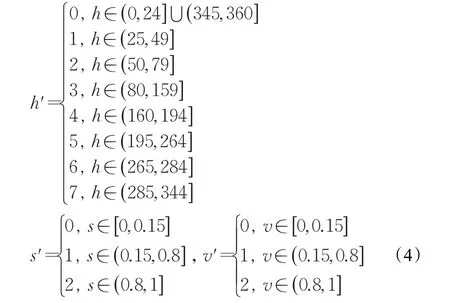
分别统计72种量化值所对应的像素点的数目，得出图像非均匀区域的72维灰度直方图。结合颜色均匀区域，得到图片颜色特征提取后的32+72=104维直方图COLOR_HIST。图2为彩色lena图的颜色梯度图和彩色直方图。

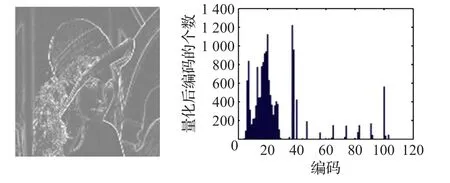
图2 颜色梯度图及直方图

1.2 图像的边缘特征提取

边缘特征的提取同样采取了分块提取的思想。在边缘获取方面，本文选用Canny边缘算子。具体算法如下：

（1）将彩色图形进行灰度化处理。

（2）用canny算子对灰度图进行边缘提取生成边缘二值图像。

（3）将边缘二值图像分割成相邻但不重叠的2×2大小的子块。

（4）结合目标子块周围三个子块对每一个子块进行编码。

（5）直方图统计索引编码。

用canny算子对灰度图进行边缘提取后所生成的图像为二值图像。对目标子块进行编码时，编码值为目标块中“1”值的个数，由于子块为2×2大小，因此共有编码值共有5种情况。为了使边缘直方图具有边缘像素的空间统计特性，结合目标子块周围的三个子块进行编码。边缘子块如图3所示。

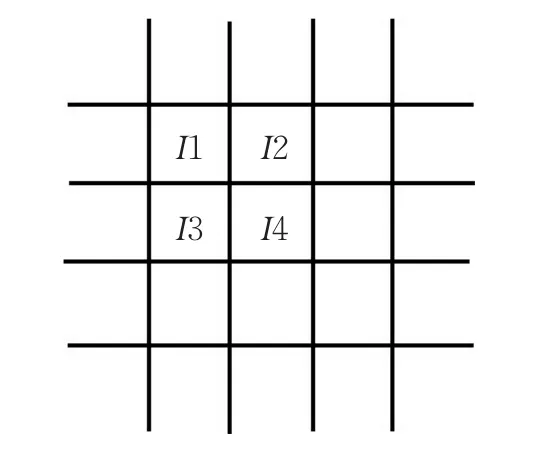
图3 边缘子块图

图3 中每个子块I的大小为2×2。例如目标子块I1中“1”值的个数为2，I2子块中“1”值的个数为3，I3子块中“1”值的个数为0，I4子块中“1”值的个数为1，则最终编码code=2×1+3×5+0×25+1×125=142。按照这种编码方案，生成625维边缘直方图。

由于子块2×2过于小，而图片中背景一般会占大部分，反应到此边缘直方图中表现为索引“0”过于突出。经过实验对比，剔除直方图索引“0”分量更有利于两幅边缘直方图的比较与计算，因此最终本文所生成的边缘直方图中剔除了“0”分量，生成624维边缘直方图FEAT_HIST。图4为彩色lena图的边缘二值图及边缘直方图。

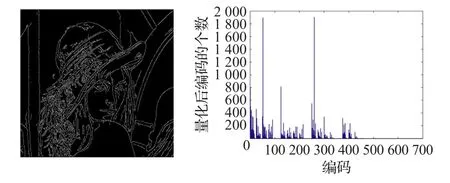
图4 边缘二值图及直方图

1.3 图像的纹理特征提取

LBP（Local Binary Pattern），局部二值模式，由于其定义简单、扩展方便、效率较高，且对光照具有不变性，因此本文选用传统LBP算子进行图片纹理特征的提取。采用3×3的邻域模板，得到8位二进制码，该二进制码为纹理直方图统计的索引码。具体过程如下：

（1）将彩色图进行灰度化处理。

（2）采用3×3邻域模板LBP算子对灰度图进行处理，得到纹理图谱。

（3）对纹理图谱进行纹理直方图统计。

生成2^8=256维纹理直方图，在本实验中剔除了编号“255”空白区域纹理索引分量。生成255维纹理直方图TEXT_HIST。图5为彩色lena的纹理图谱及纹理直方图。

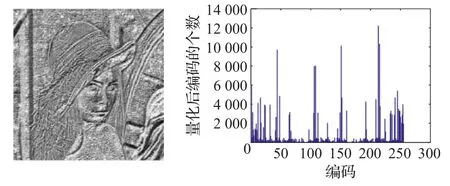
图5 纹理图谱及纹理直方图

2 图片相似度对比

传统的基于直方图的图片相似度对比算法一般采用直方图相交法[14]，余弦相似度，欧氏距离法。直方图相交法在对比两幅图片颜色特征时效果较好，但是在对比图片的边缘纹理特征时效果很差，差异很大的两幅图可能给出相似度很高的计算结果。PS考试时考生图像与标准答案图像很相似，余弦相似度法难以进行有效相似度区分。欧氏距离法的计算结果是一个距离，在PS考试阅卷中难以给出实际分数。考生答案图为在原图的基础上进行PS操作所得，对此本文通过对比原图，考生图，标准答案图三图的相似度，并提出基于三角形的欧氏距离归一化算法，计算考生图相对于原图与标准答案图的相似度来得出最后考生的实际得分。

2.1 图像特征直方图欧氏距离

本文采用欧氏距离来对比图片之间的相似度距离。运用前文所提取的特征直方图计算图片之间的颜色，边缘，纹理特征的欧氏距离。欧氏距离公式如下：

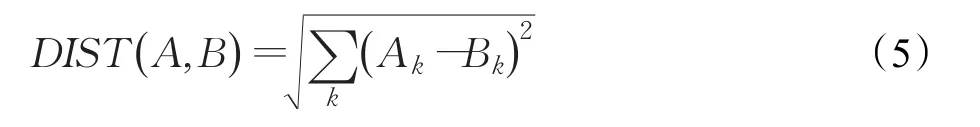
图A与图B的颜色距离记为DIS T_COLOR(A,B)，边缘距离记为 DIST_FEAT(A,B)，纹理距离记为DIST_TEXT(A,B)。

2.2 基于三角形的欧氏距离归一化算法

欧式距离归一化需找一个合适的底来进行归一化处理。在PS考试阅卷中直接以原图到标准答案图的欧氏距离以底来进行归一化处理效果不理想。本文选用原图（图A），标准答案图（图B），考生答案图（图C）的颜色，边缘，纹理特征进行两两欧氏距离计算。三幅图片相应特征直方图计算出的多维欧氏距离必满足三角不等式，即任意两边之和大于等于第三边，任意两边之差小于等于第三边。由此在平面中必能构成一个三角形（两边之和等于第三边的情况视高为0的特殊三角形）。以线段长度代表所计算出的欧氏距离，构成的相似度三角形如图6所示。

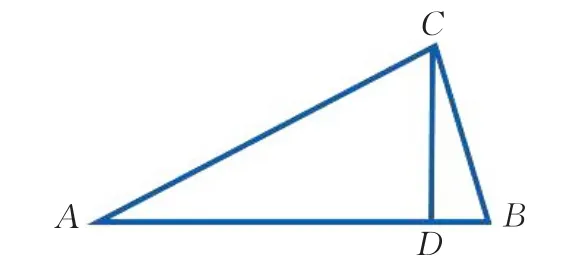
图6 相似度三角形图

其中线段AB，BC，CA的长度分别表示图A，图B，图C相应特征直方图的欧氏距离，D为C在直线AB上的投影。

定义C相对于A与B横向相似度：

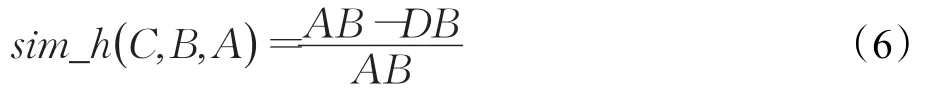
定义C相对于A与B纵向相似度：

则C相对于A与B的相似度为：

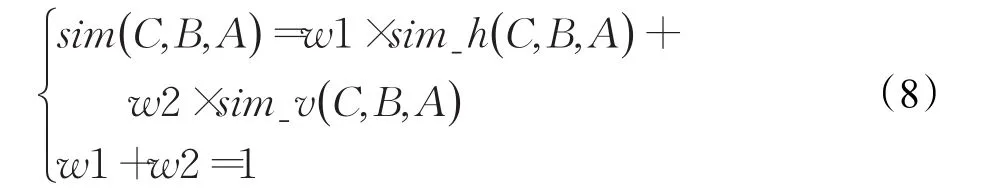
纵向相似度为横向相似度的修正，w1一般远大于w2。

2.2.1 特殊三角形的处理

有三种特殊情况需要做处理：（1）若BC距离大于2倍AB距离，则说明考生答案图与标准答案图相似度非常低，设定此种情况相似度为0。（2）若横向相似度的计算结果小于零，两图的相似度为负数，不合常理，在此本文做出截尾归一化处理，设定此种情况相似度为0。（3）若纵向相似度的计算结果小于零，设定纵向相似度为0。

C相对于A与B的相应特征相似度归一化算法具体如下：

（1）三图相应特征直方图两两进行欧氏距离计算，构成相似度三角形。

（2）若BC大于2倍AB，则相似度为0。计算结束。

（3）计算横向相似度与纵向相似度。

（4）若横向相似度小于0，则相似度为0。计算结束。

（5）若纵向相似度小于0，则纵向相似度为0。

（6）计算得到C相对于A与B的相应特征相似度。

2.2.2 计算C相对于A与B的总体相似度

赋予颜色，边缘，纹理相似度合适的权值，最后计算得到C相对于A与B的总体相似度。本文采用固定权值，颜色，边缘，纹理所给权值分别为0.3，0.35，0.35。该权值可根据考试对某技能的侧重考查而进行相应的改变。如该次考试主要考查考生对颜色敏感度，则相应增加颜色权重的值，减小其他两项的权重。总体相似度sim_total公式定义为：

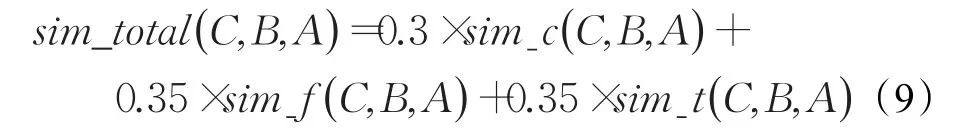
其中sim_c为颜色相似度，sim_f为边缘相似度，sim_t为纹理相似度。由此计算出考生图相对于原图与标准答案图的总体相似度。

3 实验结果及分析

本文实验所用计算机配置为：Intel®Core i7 7700k CPU（主频大小为4.2 GHz），内存大小为8 GB；实验中采用的软件环境为MATLAB 2014b，在64位Windows10平台下进行测试。经过实验训练，本文颜色和边缘的横向相似度与纵向相似度权值选取分别为：0.78，0.22。纹理的横向相似度与纵向相似度权值取值为：0.8，0.2。

3.1 实验一

实验图片除Lena外大小均为690×690。原图和标准答案图如图7所示。

图7 西瓜原图和标准答案图

考生所做答案图如图8所示。

图8 考生答案图

直方图相交法记为算法1，余弦相似度法记为算法2。该两种算法能直接得出相似度，为考生答案图与原图直接做相似度比对的方法。算法3使用欧氏距离进行考生图与标准答案图的相似度比对。计算结果为两幅图像特征直方图的欧氏距离，非相似度，在此用原图与标准答案图的欧氏距离进行归一化处理。计算公式如下：

其中DIST(A,B)为原图与标准答案图的欧氏距离，DIST(B,C)为考生答案图与标准答案图的欧氏距离。若计算结果为负数，做截尾处理相似度归一化为0。本文算法记为算法4。实验结果如表1所示。

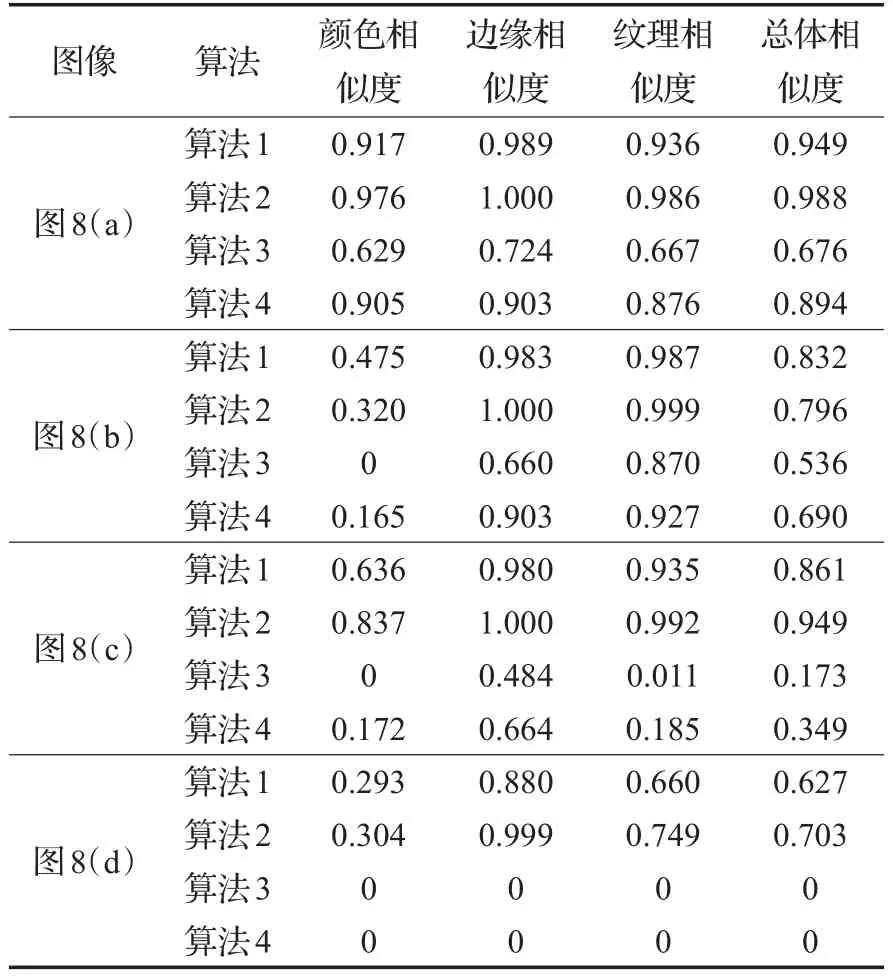
表1 三种相似度算法计算结果

通过实验结果发现，算法1在边缘和纹理相似度上表现不理想，在考生答案图和标准答案图很不相似的情况下也可能给出考生很高的分数。算法2则全都给出非常相似的结果，难以区分考生答案与标准答案的相似度。算法3未考虑考生答案图与原图的欧氏距离，计算出的相似度明显偏低。图8（a）考生在边界和纹理的处理上基本合理，相应的相似度却只有0.724和0.667。颜色处理上留白了一小块西瓜的区域，其余部分颜色处理正确，但是颜色相似度仅有0.629。本文算法通过考生答案图与原图和标准答案图的综合比较，所给出的相似度较合理，可以做到考生答案和标准答案相似度的有效度量。

3.2 实验二

本次考试要求考生去除图中的一个西瓜，并把车辆进行翻新操作。实验图片大小均为564×842。原图和标准答案图如图9所示。

考生答案图及运用本文方法所计算出的考生图相对于原图与标准答案图的相似度结果如图10所示。

图9 汽车原图和标准答案图

图10 考生答案图及相似度

其中图10（a）仅仅去除了原图车窗下的水印，该图较原图来说改动较小，与原图更加相似，其与标准答案图相似度计算结果为0.221。图10（c）颜色部分错误严重，纹理和边缘部分修改正确，所计算相似度为0.728。图10（d）为考生直接选用画笔涂抹修改所得，该种做法严重破坏了图像的纹理信息，且边缘部分处理较为毛糙，相似度所得为0.293。图10（f）与原图及标准答案图完全不相同，计算所得的相似度极低。

4 结束语

本文以答案为导向，通过提取图片的颜色，边界，纹理特征直方图来进行图片的相似度对比。并提出任意三幅图片之间的欧氏距离归一化算法，通过计算考生图相对于原图与标准答案图的相似度来给出考生实际所得分数，所给分数较为合理。对于颜色，边界，纹理相似度的权值，可根据考试侧重不同而进行修改，从而突出对考生某项技能的考核。并且该算法也可归一化D1距离[15]，曼哈顿距离等相似度度量算法。