非负局部约束低秩子空间聚类算法
解 昊,赵志刚,吕慧显,刘馨月,刘成士,董晓晨
1.青岛大学 计算机科学技术学院,山东 青岛 266000
2.青岛大学 自动化与电气工程学院,山东 青岛 266000
1 引言
在过去几十年中,子空间学习[1]和聚类问题在计算机视觉和机器学习领域成为重要的研究课题之一。通常高维的数据点是从多个低维子空间中抽取出来的,子空间聚类的基本任务是根据潜在的子空间对数据点进行聚类。根据聚类机制,目前已存在的子空间聚类方法可以分为代数方法[2-3],迭代法[4],统计方法[5-7]和谱聚类方法[8-11]。以上方法中,谱聚类是近年来最受欢迎的子空间聚类算法[12]。
谱聚类算法的关键步骤在于构建亲和度图。构建亲和度图的方案分为基于局部距离和基于全局线性表示两种。基于局部距离的方法利用成对点之间的欧氏距离建立亲和度图,如拉普拉斯特征图[13],k近邻[14],若两个数据点不相邻,则将两点之间的亲和度置为0,否则置为1。基于局部距离的方案计算简单,但是这种构建图的方式对噪声和异常值敏感。基于全局线性表示的方案假设每个数据点可以在一个过完备的字典(即X=DZ,其中D是过完备的字典)中被线性地表示。通过对表示矩阵Z应用不同范数正则化,可以得到不同亲和度来构建图,如线性平方回归[8],稀疏子空间聚类[9],低秩表示[10]等。
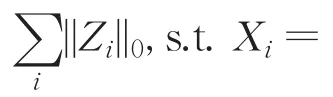
与基于稀疏方法相比,基于低秩的方法旨在找到所有数据的最低秩表示,即rank(Z),s.t.X=XZ。此方法更适合追求数据空间的全局和内在信息。然而,低秩表示算法不能利用数据之间局部线性结构,这将导致构造的亲和度矩阵通常是密集的,并且低秩表示中的负值在构建亲和度矩阵上没有任何意义。
为了兼顾数据的全局和局部结构,本文提出了非负局部约束低秩子空间算法,该算法在低秩表示的基础上,将数据的局部稀疏结构作为约束集成到统一公式中。此外,原始数据作为字典不具有代表性,基于学习的字典对噪声有良好的鲁棒性。考虑到最终结果的准确性,在预处理数据时,采用Wei[20]基于矩阵分解的分析,对字典进行更新。
2 相关工作
2.1 子空间聚类问题
令 X=[x1,x2,…,xn]是来自于 k个线性子空间的m维数据向量的集合,其中子空间S的维度i为ri。子空间聚类的任务是将存在于同一个子空间中的数据向量分离出来。为了标记符号简单,可以假设X=[X1,X2,…,Xk],其中Xi由存在于子空间Si中的数据向量组成。同时,假设子空间Si相互独立,di表示为Xi中的向量数。那么存在至少一个块对角矩阵Z=diag{Z1,Z2,…,Zk}满足等式:

其中第i个块Zi的维度为di×di。式(1)具有无穷多的解。任何一个解都可称为表示系数矩阵。值得注意的是,矩阵Z的块对角结构直观显示了数据的分割(每个块对应于一个簇。因此,聚类任务相当于找到块对角线表示矩阵Z)。
2.2 低秩表示算法
低秩表示算法旨在探索多个子空间结构,从而找到一组数据向量的最低秩表示。
对于无噪声的情况,低秩表示算法将数据本身作为字典,并寻找最低秩表示矩阵Z:

由于秩函数不是凸的难以求得最优值,式(2)最优化问题可以放宽到以下凸优化问题:

对于存在噪声的情况,低秩表示算法通过向目标函数(3)添加列和范数项处理噪声数据,使得噪声稀疏:

虽然实验结果表明[10]式(4)对于噪声有强鲁棒性,但是当噪声影响严重,或者异常值所占百分比较大时。使用原始数据X本身作为字典将导致聚类效果明显下降。Wei[20]对于字典提出了一种改进的低秩表示方法:

直观地,该模型消除了大部分噪声,并采用干净数据作为字典,当数据本身严重损坏时,最终的聚类效果比低秩表示算法有明显提升。
3 非负局部约束低秩子空间算法
3.1 非负局部约束低秩模型
在2.1节中,说明了对于块对角矩阵Z如果字典是过于完备的(比如用数据本身作为字典)可以有无穷多个可行解,为了解决这个问题,对所求的表示矩阵Z加入稀疏与低秩约束:

式(6)中β>0是正则项参数平衡稀疏性与低秩性,表示矩阵Z的每一列zi揭示了数据xi与字典A的线性关系。然而,求解式(6)是一个NP难问题,借由Liu[10]与Vidal[9]的处理将式(6)转化如下:

同时,也要考虑到噪声的影响,加入噪声项E的同时,对字典进行更新:

该模型具体来说,每个数据点由其他数据点的线性组合得到,表示矩阵Z是非负且稀疏的[21]。非负值确保每个数据点位于其邻点的凸包中,稀疏性确保所涉及的邻点尽可能少。除了非负稀疏约束之外,表示矩阵Z强制为低秩,使相同子空间上的数据点聚类成同一个簇。
3.2 线性交替方向乘子法求解非负局部约束低秩模型
引理1令[U,S,V]=SVD(D),则最优化问题,s.t.D=DZ的解是矩阵D的形状相互作用矩阵,即Z*=VVT,目标方程最优值为:||Z*||*=rank(D)。
根据引理1可以将式(8)近似地转化为如下两式:
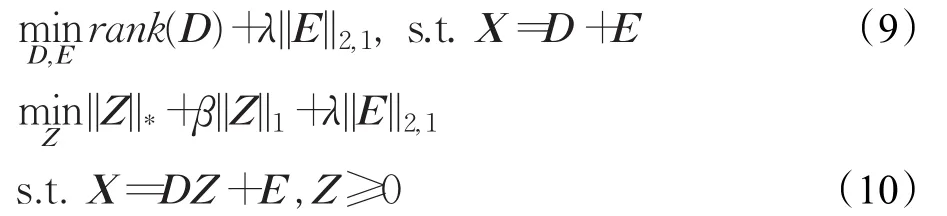
对于式(8),虽然在求解过程时固定其他变量求解单一变量可以确保函数为凸函数,但计算量仍非常巨大。因此在确定字典时,基于Wei[20]的分析结果,采用无噪声时的低秩表示最优解等于数据形状相互作用矩阵[20]方案。
式(9)用核范数近似替代秩函数(rank),利用增广拉格朗日方法去除约束条件后,借由Lin[22]提出的非精准拉格朗日乘子算法(ALM)迭代求解最优化问题:

算法1求解式(9)
输入:数据矩阵X,参数λ>0
初始化参数:E0,Y0,u0>0,umax>u0,ρ>1,ε>0
1.更新D:

2.更新E:

3.更新乘子Y:

4.更新 u :uk+1=min(ρuk,umax)
5.k←k+1
结束循环
输出:新字典D
对于式(10),交替方向乘子法(ADM)在求解时需要引入两个辅助变量,每个变量迭代都需要庞大的矩阵计算。因此,采用线性交替方向自适应法(LADMAP)[23]解决此最优化问题。
首先,引入辅助变量H使目标函数变量可分离:
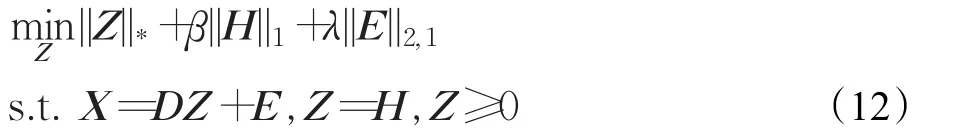
式(12)的增广拉格朗日方程为:

为后续计算简便,式(13)化简为:

线性交替方向自适应法(LADMAP)通过求解单一变量时,固定其他变量为最小值来交替更新变量Z、H和E,其中二次项在前一次迭代中被其一阶导数近似代替,然后添加近似项Z-Zk完成变量更新[22]。通过一些代数运算,变量Z、H和E更新方案如下:


其中∇为关于Z的偏微分操作,Θ、S、Ω分别是奇异值阈值操作、收缩阈值操作、l2-1最小值操作[10],特别的,式中的
完整迭代算法流程见算法2。
算法2求解式(10)
当||X-DZk-Ek||F/||X||F≥ε1或者ε2时:
1.按照式(16)更新 Z
2.按照式(17)更新 H
3.按照式(18)更新 E
4.更新乘子Y1:

5.更新乘子Y2:

6.更新ρ:
输入:数据矩阵X ,字典D,β>0,λ>0
初始化参数:


7.更新 u :uk+1=min(ρuk,umax)
结束循环
输出:系数矩阵Z*,噪声矩阵E*
3.3 构建亲和度矩阵
得到表示系数矩阵Z*之后,可以从中导出图形邻接结构和亲和度矩阵。实际上,由于存在数据噪声,数据点xi对应的表示系数向量密度较小,直观表现为数值较小。由于构建亲和度矩阵时只对数据的全局结构感兴趣,所以可以对每个样本的系数向量进行归一化处理(即),并设定阈值将较小值置为0。经过阈值操作后会得到真正的稀疏表示系数矩阵,并将亲和度矩阵W 定义为
3.4 非负局部约束低秩子空间算法
定义亲和度矩阵W后,剩下工作为构建亲和度图,图中的每个顶点对应着每个数据点xi,两顶点xi,xj之间连线的权重对应着亲和度矩阵W的元素wi,j,采用谱聚类算法如归一化切割[24]对亲和度图进行划分,划分得到的每一部分为一个簇,即完成聚类操作。完整流程见算法3。
算法3非负局部约束低秩子空间算法
输入:数据矩阵X,子空间数目k,阈值θ
步骤:
1.通过算法1得到干净字典D
2.通过算法2得到表示系数矩阵Z*
3.对表示系数矩阵Z*数据归一化:,并根据给定阈值θ筛选值:

4.对亲和度矩阵W应用归一化切割谱聚类算法,根据输入的k值,分成k个聚类。
4 实验
本章将评估非负局部约束低秩子空间算法(NLRSI)对合成数据和实际计算机视觉任务(运动分割和手写数字聚类)的性能。为了直观表达效果,将与基于谱聚类的最先进的子空间聚类算法,如稀疏子空间算法(SSC)[9],低秩表示子空间算法(LRR)[10],鲁棒形状相互作用矩阵算法(RSI)[20]和非负低秩稀疏表示算法(NNLRSR)[25]进行对比。选择这些方法作为基准,是因为这些算法在上述任务中的表现效果很好。为了进行公平比较,根据Tron[26]定义的子空间聚类误差作为性能的度量:子空间聚类误差=错误分类数据点/总数据点。
对于比较的算法,采用引用文献中的参数作为输入参数,其中对于Hopkins155运动分割数据库[27],稀疏子空间算法λ=20;低秩表示子空间算法λ=4;鲁棒形状相互作用矩阵算法λ=10;低秩稀疏表示算法λ1=100,λ2=10;非负局部约束低秩子空间算法β=5,λ=4.2。对于USPS手写数字数据库,稀疏子空间算法λ=0.05;低秩表示子空间算法λ=0.18;鲁棒形状相互作用矩阵算法 λ=0.01;低秩稀疏表示算法 λ1=0.01,λ2=10;非负局部约束低秩子空间算法的参数为β=0.17,λ=5。
4.1 合成数据

图1 各个算法对噪声污染鲁棒性
当 p=0与 p=0.3时,图2与图3显示了亲和度矩阵W 或者表示系数矩阵Z*(对于SSC,LRR,RSI算法)的块对角结构。

图2 p=0时得到的亲和度矩阵或者系数矩阵块对角结构
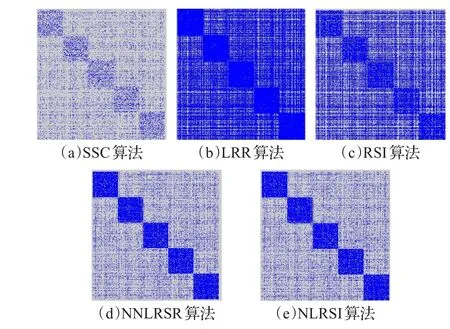
图3 p=0.3时得到的亲和度矩阵或者表示系数矩阵块对角结构
通过图2与图3的对比可以看出,非负低秩稀疏表示算法(NNLRSR)与非负局部约束低秩算法(NLRSI)对噪声的鲁棒性能较好,这表明通过局部约束强制更改矩阵结构可以消除大量无关噪声,使得聚类效果提升,这也在图1的准确率变化趋势图中有所体现。
4.2 运动分割
运动分割是指从视频序列中提取一组二维点轨迹,将轨迹对应于不同的刚体运动。这里,数据矩阵X的尺寸为2F×N,其中N是二维轨迹的数量,F是视频中的帧数。在仿射投影模型下,n个不同运动对象相关联的二维轨迹位于n个仿射子空间的组成的R2F空间中,至此运动分割问题转化为将所有的二维轨迹聚类到不同的子空间中,每个子空间对应于一个运动对象。
本部分采用Hopkins155数据库[27](图4为部分视频序列效果截图)测试算法效果,Hopkins155数据库由155个序列组成,包括104个室内场景序列,38个户外交通场景序列和13个非刚性序列。其中有120个序列具有2个运动物体,其余35个序列具有3个运动物体。为了测试简便,根据运动物体数量将数据分为两组,分别对这两组数据进行实验。

图4 Hopkins155数据库部分序列聚类效果截图
表1显示了Hopkins155数据库中155个序列聚类误差,图5与图6展示了155个序列应用非负局部约束低秩子空间算法(NLRSI)各自的聚类误差,明显的,二物体比三物体聚类误差更小。同时从表1中的数据可以看出NLRSI算法的聚类误差比其他算法误差小,虽然低秩表示算法(LRR)的中位值更低,但是从平均值结果来看,低秩表示算法对于某些序列的聚类效果不稳定,导致了误差过大,拉高了平均值。

表1 各类算法在Hopkins155数据库中的聚类误差 %
4.3 手写数字

图5 Hopkins155数据库NLRSI算法两物体序列聚类错误率

图6 Hopkins155数据库NLRSI算法三物体序列聚类错误率
手写数字聚类是指由不同人笔迹构成的一组数字图像,将数字相同的图像分离出。这里采用美国邮政手写数字数据库(USPS)测试算法的聚类效果。图7显示了部分数据样本。该数据库包含9 298张图像,每张图像为一个数字(0~9任意一个,如图7所示),图像的大小为16像素×16像素,因此数据矩阵X的维度为256。由于数据样本过于庞大,对每一个数字随机抽取100张图像,共1 000张图像作为数据样本。同时为了测试聚类效果的多样性,聚类的数目k设置为2~9,即分别抽取2个数字到9个数字评估聚类结果。

图7 USPS数据库部分数据样本
从表2可以看出非负局部约束低秩子空间算法(NLRSI)的聚类误差相比其他算法较小,当聚类数目k处于小值的时候,各个算法的聚类误差相差很小,随着k值的增大,聚类误差都在增大,图8所示的子空间数据结构图可以直观看出随着簇的数量增多,噪声点随之增多,这是由于聚类数目增多会导致一些数据点同时存在于多个子空间中,造成重复计算。从图9变化趋势图中观察到NLRSI算法聚类误差率增长较为缓和,说明NLRSI算法对于这些异常点的甄别较为精准。

表2 各类算法在USPS数据库中的聚类误差%

图9 各类算法随着聚类数目增多聚类误差变化走势图
5 总结
本文提出了非负局部约束低秩子空间算法(NLRSI),该算法利用数据的局部稀疏结构和子空间的全局低秩特征,构造体现数据向量之间特点的亲和度矩阵。理论分析保证了算法获得的最优亲和度矩阵具有良好的聚类效果。同时实验结果表明,非负局部约束低秩子空间算法在运动分割和手写数字聚类任务中,优于现存的几种最先进的聚类算法。但是该算法也存有不足之处:为了保证聚类准确性,优先对数据字典做去噪处理,增加了运算时间;其次对于聚类数目较多的数据,聚类结果误差较大。未来的工作将在保证准确性的同时,缩短运算时间,减少聚类误差。

