基于SPSO与ISKPCA的RdR散点图识别分类研究

岳大超，甘良志，刘海宽，余南南

江苏师范大学 电气工程及自动化学院，江苏 徐州 221116

1 引言

长久以来，心血管疾病一直是威胁人类健康的主要问题。目前，心血管病死亡占城乡居民总死亡原因的首位，预计到2030年大约要有2 330万人死于心血管病[1]。面对这种趋势，对心血管病的早期诊断与预防显得尤为重要。

传统的诊断方法是患者到医院，医师对其进行心电图检查，进而给出诊断结果[2]，任务繁重且需要医师有丰富的临床经验和专业知识。而稀缺的医疗资源，很难满足数量庞大患者群体的要求。为了提高就诊效率，方便性和快捷性，出现了自动化诊断技术，辅助医师进行诊断。

心率变异是指心动间期之间的时间变异数，其研究对象是心动间期。人的心率不是一成不变的，两次心搏之间存在着微小的时间差异，计算心动间期的差异，即可了解心率变异性（Heart Rate Variability，HRV）。心率变异性可以评估心脏交感神经与副交感神经对心血管活动的影响，蕴含着心血管方面的大量信息[3-4]。临床研究表明，心率变异性的降低是心肌梗死、高血压、心绞痛等心血管疾病发病的症状。因此，心率变异性的研究，在评价心血管系统功能、预测心血管疾病的发作，以及为心血管疾病的早期诊断具有重要的意义[5-6]。

Poincare散点图是心率变异性一种重要的研究方法。通过使用连续的心搏间期在直角坐标系中绘制图形，反映相邻心搏间期的变化，能显示心搏间期的特征。Poincare散点图有多种形态，包括彗星状、扇形等，不同的形状反映不同的心脏状态[7-8]。虽然Poincare散点图是一种有效的心率变异性分析方法，但是并不能体现其随时间变化的趋势，对于某些心血管疾病、身体健康状况等不能很好地体现其心率变异性性质。于是，一些学者提出了改进策略，即一阶差分散点图，通过相邻心搏间期的差值来绘制散点图。然而，这种方法又丢失了原有的心搏间期绝对值信息。因此，在文献[5]中，将二者结合起来，提出了一种RdR散点图，以此来同时反映心搏间期及其变化。

目前，对于心率变异性分析的研究很多[9-12]。但是，并没有根据散点图来有效识别、区分不同的心血管疾病，实现心电自动化诊断的研究。本文即是通过简化粒子群算法（Simplified Particle Swarm Optimization，SPSO）与集成稀疏核主分量分析（Integration Sparse Kernel Principal Component Analysis，ISKPCA）方法来对RdR散点图进行识别分类，为心电自动化诊断的实现提供一些基础。

2 简化粒子群算法

基本粒子群算法（Particle Swarm Optimization，PSO）是一种智能优化算法，算法首先在搜索范围内随机初始化一群粒子，之后不断迭代，迭代过程中更新两个参数：一是粒子自身的最优位置；一是种群的最优位置；直至达到终止条件[13]。

胡旺等人把基本粒子群算法进行了简化，称为简化粒子群算法（Simplified Particle Swarm Optimization，SPSO）。假设在D维搜索空间中，设置S个粒子，迭代T次，第i个粒子在d维的位置用Xid表示，用 pBestid记录该粒子最好的位置，用gBestd记录种群最好的位置。简化后公式为：

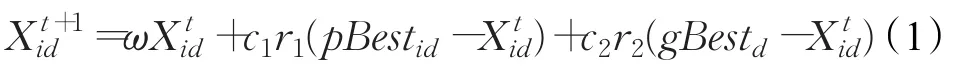
式（1）中，右边第一项是“粒子惯性”，为个体历史对现在的影响，利用惯性权重ω来调节影响；第二项是“自我认知”，是粒子对自身的思考，c1是学习因子；第三项是“社会引导”，表示粒子对历史上最优粒子的模仿，c2是学习因子，r1，r2是服从U(0,1)分布的随机数。该算法仅通过粒子的位置进行更新迭代，把方程从二阶降为了一阶，并通过理论和实验证明了该方法的有效性、优越性，这种改进使得整个过程变得更为简单。

3 集成稀疏核主分量分析

主分量分析是一种典型的无监督算法，常用于解决原始空间的线性问题[14-15]，而为了在特征空间中用线性方法解决原始空间的非线性问题，B.Scholkopf等人提出了核主分量分析（Kernel Principal Component Analysis，KPCA）[16]。

其中，矩阵K是N×N的矩阵，也称核矩阵。则式（3）问题转换为：

过程可以直接在K上运算：

本文选择一种常用的核函数，径向基核函数来进行计算。当选择径向基核函数时，会有明显的过学习问题，主要是由于径向基核函数对应的特征空间是无限维的，通过该方法得出的主分量的次数与给定样本的维数无关，而与样本数量有关。为解决这个问题，引入了稀疏化方法，即为稀疏核主分量分析（Sparse Kernel Principal Component Analysis，SKPCA）。

在核主分量分析中，特征向量能用样本{φ(x1),φ(x2),…,表示为 ，也就是说特征向量͂是全部样本的线性组合，这为特征向量的稀疏化提供了一种思路。通过近似基求解算法，来求{φ(x1),φ(x2),…,φ(xN)}的近似基，从而得到的稀疏化方法。

近似基求解的具体步骤是：

（1）建立集合Xl={φ(x1)}为近似最大无关组，XA=ϕ。

（3）如果得到极小值value≤ε，则把对应的元素加到XA当中，否则为Xl。ε是线性相关截尾误差，在有限的样本中求无限维空间的基几乎没有稀疏性，因此选择近似计算。

（4）返回步骤（2），直至完成所有的计算，计算结束。

其中，步骤（2）中的求解过程如下，令

可知式（11）是特征值与特征向量的问题，即

推导得：

其中，K(m,:)表示核矩阵K的第m行，K(:,n)表示第n列表示1行N 列的行向量。式（12）也就变成了：

为典型的特征值与特征向量问题。

虽然稀疏化可以控制学习机的学习能力，防止过学习，但是稀疏化方法仍然可能会丢失数据集的某些重要特性，即欠学习问题。因此，有必要引入集成方法，称为集成稀疏核主分量分析（Integration Sparse Kernel Principal Component Analysis，ISKPCA）。由于核主分量分析是一种无监督学习，不能从外部获得指导，即不能对某次学习结果进行奖赏或惩罚，所以，本文选择简单平均的方法。SKPCA的集成方法具体步骤流程如下：

（1）设置重复的次数Re。（2）计算核矩阵K=ΦTΦ。

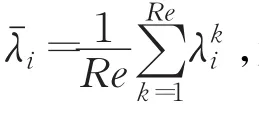
4 Rd R散点图

令△RRn=RRn-RRn-1，RRn为第n个心搏间期。RRn为横坐标，△RRn为纵坐标，逐次绘点，即得RdR散点图。为验证本文算法的有效性，使用的数据为MIT-BIH数据库中的心电数据作为测试样本，实验过程中用到的数据编号如表1所示。

实验当中，使用MATLAB绘制来绘制RdR散点图，取编号100中的部分数据来绘制RdR散点图，示例如图1所示。

表1 本文使用的MIT-BIH数据库的数据

图1 编号100的RdR散点图

5 实验

将ISKPCA用于RdR散点图的分类识别，需要先建立ISKPCA模型，然后选择控制指标。平方预测误差（Squared Prediction Error，SPE）是常用的控制指标。

对于第i个样本Xi，假设经过SKPCA求得其前n个主分量为t1,t2,…,tn，对应的特征值为 λ1,λ2,…,λn。用表示特征空间N个主成分的重构向量同理则样本 X 的SPE定义为：

接下来要获取样本，将表1中所示的23组数据使用MATLAB绘制成RdR散点图。在每个散点图中，选择1 000个RR间期来绘制散点图，即至少10分钟的数据，依据MIT-BIH的360 Hz采样频率计算，每幅散点图大约需要使用216 000个心电数据点。为了尽可能多地获得训练样本，采用每次移动10个RR间期来绘制散点图，共获得样本2 819例。算法具体步骤如下：

（1）读取图像数据，对图像进行缩放到同一规格，转成灰度图，将一幅图的多维矩阵数据转换成一维，并对样本进行分类标记，分别用1、2、3、4、5对应着正常窦性心律、非偶联早搏、二联律早搏、三联律早搏以及混合早搏。

（2）对数据进行Z-score标准化处理。公式如下：

其中，μ、σ分别是数据的均值与方差。

（3）分别对每类样本采样，随机抽取其中85%的数据作为训练样本，剩余的15%作为测试样本。

（4）使用简化粒子群算法搜寻参数，包括求解近似基的误差参数ε、高斯核函数参数gamma以及核主分量分析控制限t的值，以准确率为适应度函数，分别对每类样本求解近似基、特征值、特征向量。

（5）分别计算每个测试样本的SPE，其值与某类样本的SPE差值最小者为测试样本的预测类别，与实际类别比较，计算准确率，若满足要求则步骤（6），反之返回步骤（4）。

（6）使用所得分类模型，进行样本交叉实验，测试算法性能。

本文分类模型参数最终选择为：ε=250，高斯核函数参数gamma=600，主分量控制t=90%，集成个数Re=10。经过多次样本交叉验证，使用KPCA平均识别率为72%，SKPCA的平均识别率约为91%，集成SKPCA的平均识别率为98.6%。与文献[17]中使用BP神经网络来实现3种心律识别的97%的正确率相比，本文算法准确率有所提高。由此可以看出，RdR散点图可以反映上述几种心律的特征，另外，也体现了使用本文算法来进行RdR散点图分类识别的有效性。

本文使用简化粒子群算法的参数：种群规模是20，进化100代，搜索空间依据实验测试设置在[0，1 000]。从测试样本中随机选择某一类的心电数据样本，如图2选择到实际类别为“3”的一些测试样本集，将其分别与各个类别计算其SPE的差值，结果如图2，可以看到其与类别为“3”的SPE差值最小，分类正确；图3是随机抽取部分样本的预测结果与实际标记样本对比，可以看到全部分类正确。

图2 测试样本与各类的SPE差值

6 结束语

图3 部分预测结果与实际样本对比

核主分量分析存在着过学习的问题，根据统计学习理论可知，稀疏化方法可以控制学习机的学习能力，防止过学习，而且通过稀疏化可以削减样本数量，减少计算量，而为了应对由于稀疏化使某些特征被遗漏的问题，即欠学习，又引入了集成方法。本文用MIT-BIH中的心电数据来验证本文算法的有效性，算法使用心电数据绘制RdR散点图，通过简化粒子群算法对集成稀疏核主分量分析的参数进行寻优，以正确识别率为适应度函数，并用所学习到的分类模型来对五种心律的RdR散点图进行分类识别，实验结果显示，分类效果较好。但一方面，由于本文使用的数据样本及类别相对于庞大的心血管疾病种类而言都较少，使得不能非常全面、客观地反映所有问题；另一方面，本文所述方法，步骤较为繁琐，计算周期长。接下来的研究重点是：收集更多的心电样本数据；寻找更简单，更有效的方法、更高效的方法。为了实现心电自动化诊断还需要进一步的研究。