球壳屈曲特性试验与理论研究
张 猛,张 建,,唐文献*,王纬波,高 杰,3
(1.江苏科技大学 机械工程学院,镇江 212003) (2.中国船舶科学研究中心,无锡 214082) (3.江苏省道路载运工具应用新技术重点实验室,镇江 212003)
国家工信部装备工业司将深海探测装备列为未来十年海洋工程装备的发展方向与重点,要求大力发展载人深潜器、无人潜水器等水下探测装备.耐压壳作为载人潜水器的重要组成部分,起着保障下潜过程中内部设备正常工作和人员安全的作用,其重量占潜水器总重的1/4~1/2[1].现有深海耐压壳多为球形结构,球形耐压壳的屈曲特性直接影响结构的安全性和经济性,故对其屈曲特性的研究十分关键.
壳体屈曲特性通常可以用3种方法进行分析:解析法、试验法和数值法.解析法采用理论公式算出理想结构壳体的屈曲载荷,但很难分析包含几何非线性和材料非线性现象的缺陷壳体屈曲特性,致使计算结果与试验结果相差甚远,且解析法无法计算复杂形状、边界或载荷的壳体屈曲问题.因此,设计中用解析法求出的屈曲载荷通常必须乘以一系列衰减系数来给出壳体最终失稳载荷,例如,CCS2013[2]、GL2009[3]等潜水器规范中对耐压壳的屈曲计算,NASA SP-8007[4]等规范中对柱形壳体、球形壳体的屈曲计算.文献[5]中研究表明,现有规范中的壳体屈曲计算方法偏保守.试验法是研究壳体屈曲特性最为直接的方法,但试验法具有周期长、费用高,需要复杂试验设备等缺点,在前期设计阶段,进行大量的试验研究不可取.数值计算因其成本低、精度高而被广泛使用,当然复杂问题仍然需要数值法和试验法联合研究.
基于数值法的壳体屈曲特性研究途径主要包含:线性屈曲分析和非线性屈曲分析.其中,线性屈曲分析无法考虑缺陷影响及非线性特性,仅能分析理想线弹性壳体的屈曲特性,致使计算结果与试验结果相差甚远.非线性屈曲分析则考虑了初始缺陷、材料塑性、结构大变形等因素,已成为壳体屈曲特性研究的主流方法,通过缺陷壳体的几何和材料非线性分析,可直接算出壳体的实际屈曲载荷,无需考虑任何衰减系数[6-7].数值法已成为研究球形壳体屈曲特性的主流方法.文献[8-9]中采用非线性有限元法,分析了不同壁厚条件下球形钛合金耐压壳的极限强度,并对4个球形耐压壳的缩比模型进行静水压力试验,验证了计算方法的正确性;文献[10-12]中认为对于深海载人潜水器耐压球壳可以直接根据有限元数值法确定其极限强度.但是,由于非线性特性和缺陷对壳体屈曲特性影响非常大,数值法的合理性评估也很少见于公开文献,故合理的球形耐压壳屈曲特性分析方法有待进一步研究.文中对SUS304不锈钢小球进行静水压力试验,且在对试验球壳进行无损测厚试验、三维扫描试验的基础上建立球壳的真实模型,并对其展开数值分析与水压试验结果对比验证;对凹坑缺陷、轴对称缺陷及一阶模态缺陷的球壳模型展开有关规律性的系统有限元分析,得到最接近试验值的缺陷形式.文中研究结果为以后耐压球壳极限承载力的预测评估提供了参考.
1 材料与方法
以4个不锈钢球壳为试验对象,进行了静水压力试验等一系列的试验,以获得球壳的几何及屈曲特性.并且,通过材料拉伸试验获得了相关材料属性.
1.1 试样制作及材料试验
为了检测试验的可靠性,加工了4个名义半径为50 mm的球壳进行试验测试,分别命名为1#,2#,3#,4#.每个试验球壳都由2个半球焊接而成,焊接后的焊缝经过了打磨与抛光.每个半球都由304不锈钢板件冲压成型.304不锈钢的材料属性按照GB/T 228-2010的规定由单轴拉伸试验获得.
材料拉伸试样为圆柱形不锈钢哑铃试样,横截面直径为10 mm,原始标距为50 mm.使用微机控制电子万能试验机(10 t)进行材料的拉伸试验(图1),获取名义应力σ与名义应变ε关系曲线,并计算出真实应力与塑性应变,用于数值计算.
εtrue=ln(1+εnom)
(1)
σtrue=σnom(1+εnom)
(2)
(3)
式中:εtrue、εnom和εpl分别为真实应变、名义应变和真实塑性应变;σtrue、σnom分别为真实应力和名义应力.
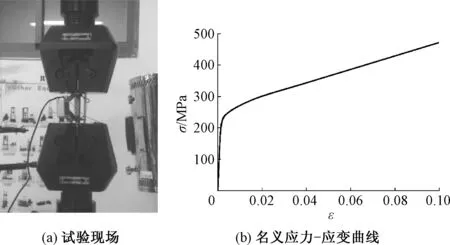
图1 304不锈钢拉伸试验Fig.1 Tensile test of 304 stainless steel
1.2 试验装置与方法
试验球壳需进行无损测厚试验和三维扫描试验,以获得球壳的几何参数.在两个试验之后进行静水压力试验,获得其屈曲特性.静水压力试验设备为本课题组自主研发,压力舱的内径为200 mm, 高为400 mm,使用水作为压力介质,其基本原理如图2.
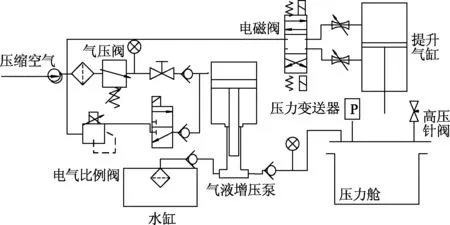
图2 设备原理Fig.2 Equipment principle
该试验设备压力源为气液增压泵,采用PLC控制,通过对驱动气源压力的调整,可得到相应的增压后的水压,并可实现对水压的无级调节.压力舱内的水压通过压力传感器(量程:0~10 MPa,精度:±0.1%)实时采集.
1.3 试验过程与结果
首先,使用超声波测厚仪(精度:±0.001 mm),对1#~4#球壳开展无损测厚试验,如图3.按照设备使用要求进行标定,标定对象为304不锈钢钢板,先使用数显千分尺(精度:±0.001mm)测出钢板厚度,再与无损超声波测厚仪结果对比,两者误差为0.001mm;接着,对4个球壳表面的42个点进行厚度测试,每个点测3次取其均值,这些点分布在球壳的4条经线和10条纬线上,赤道部位为焊缝.试验得出4个球壳的平均厚度分别为0.333、0.352、0.348、0.323 mm.
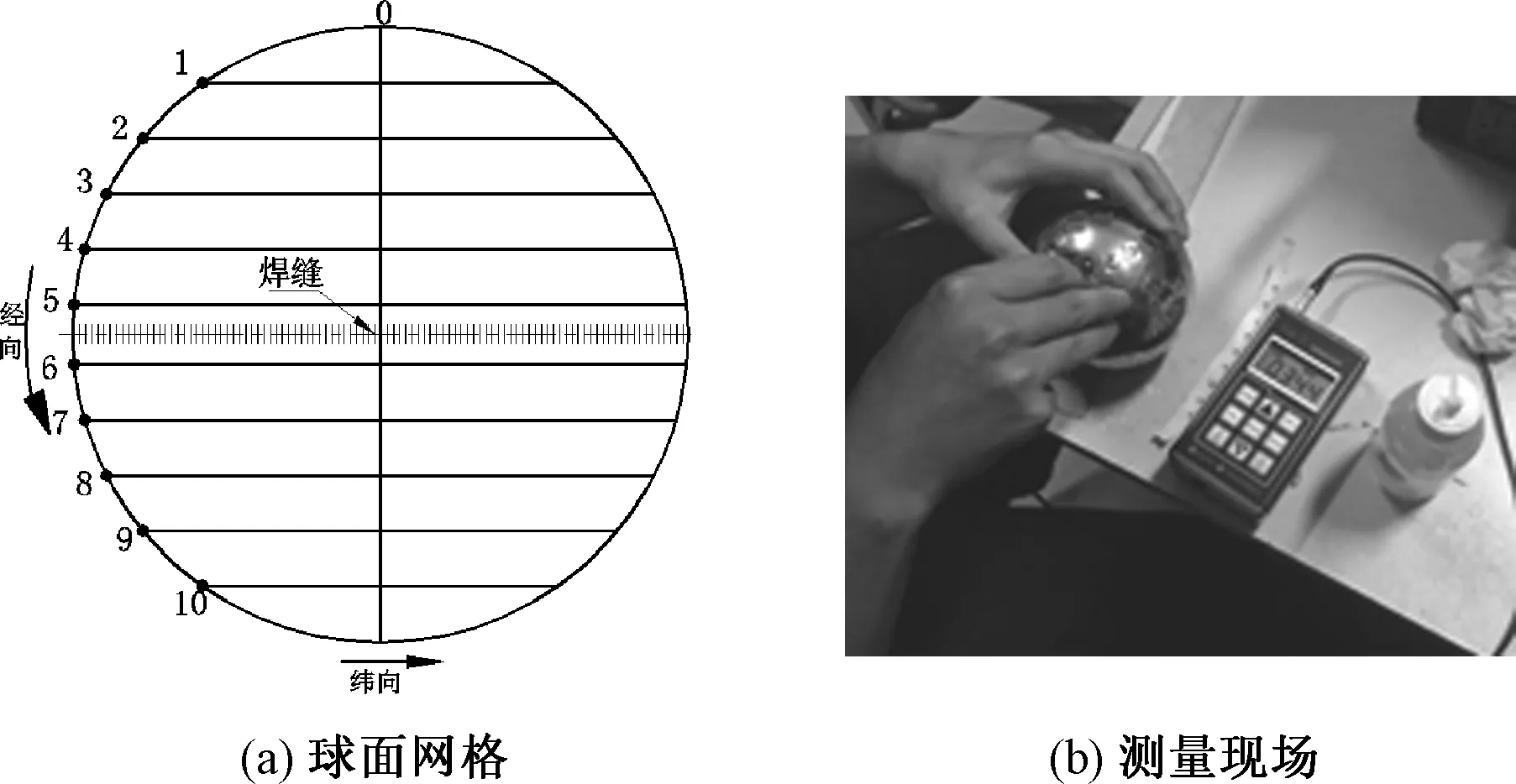
图3 壳厚的测量试验Fig.3 Measurement of shell thickness
其次,采用Open Technologies公司的3D扫描仪(精度:±0.01mm),测出1#~4#球壳的真实外轮廓,如图4.由于球壳为不锈钢材料,光洁度很高,首先需要在球壳表面喷洒一薄层显影剂,用以防止反光影响扫描精度.扫描仪对球壳外轮廓进行分片扫描并记录,并把分片扫描数据拼接组合,形成stl格式的三维几何模型,用于球壳的圆度和球度分析,并为理论计算提供相关模型、数据.

图4 球壳的三维扫描过程Fig.4 Three-dimensional scanning process of spherical shells
三维扫描试验得到的球壳模型,由Geomagic Studio软件进行逆向处理,获得iges格式文件,然后将逆向处理文件导入UG进行曲面缝合,形成三维几何模型.以球壳的球心为原点,焊缝所在平面为XY平面,沿X或Y方向导出近似圆形的截面图,使用AUTOCAD在圆周上等分80个测量点进行半径测量.
根据式(4)求得圆度Rcir:
Rcir=Rmax-Rmin
(4)
式中:Rmax为最大半径;Rmin为最小半径.
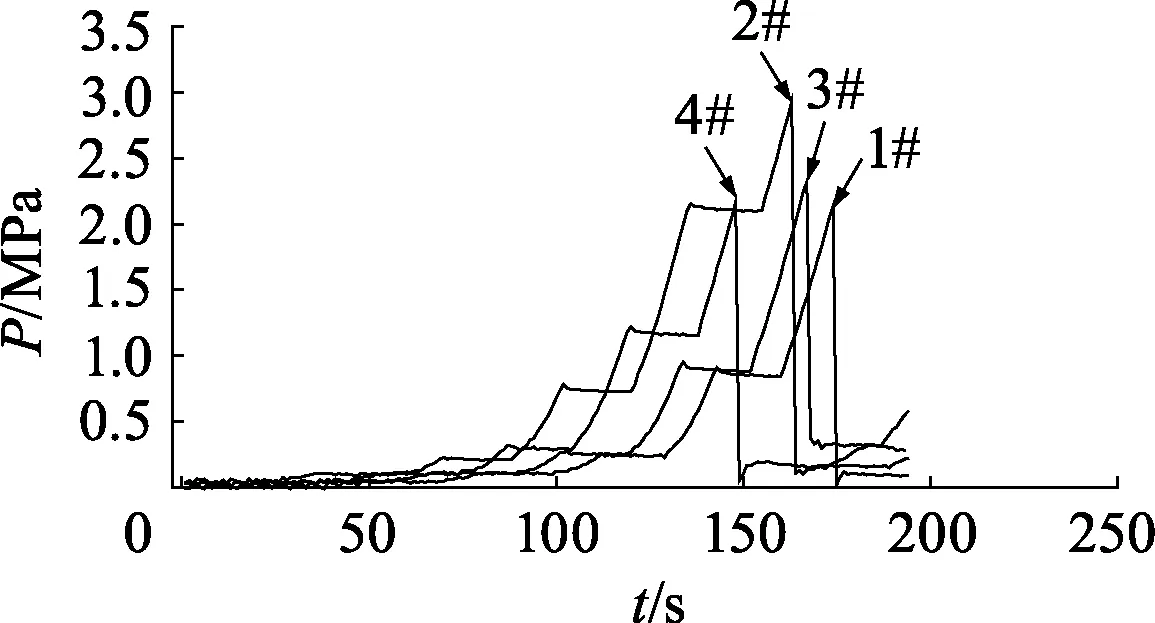
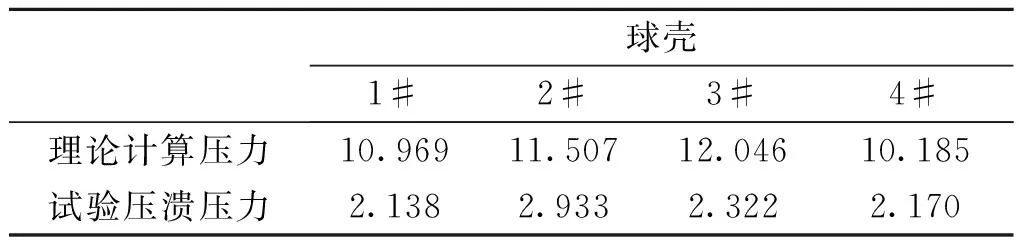
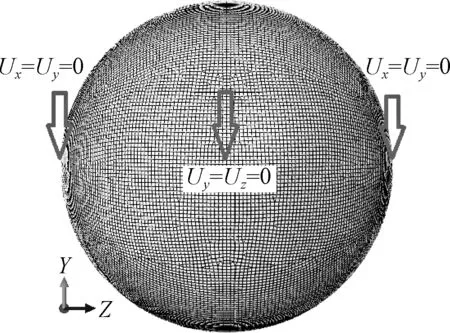
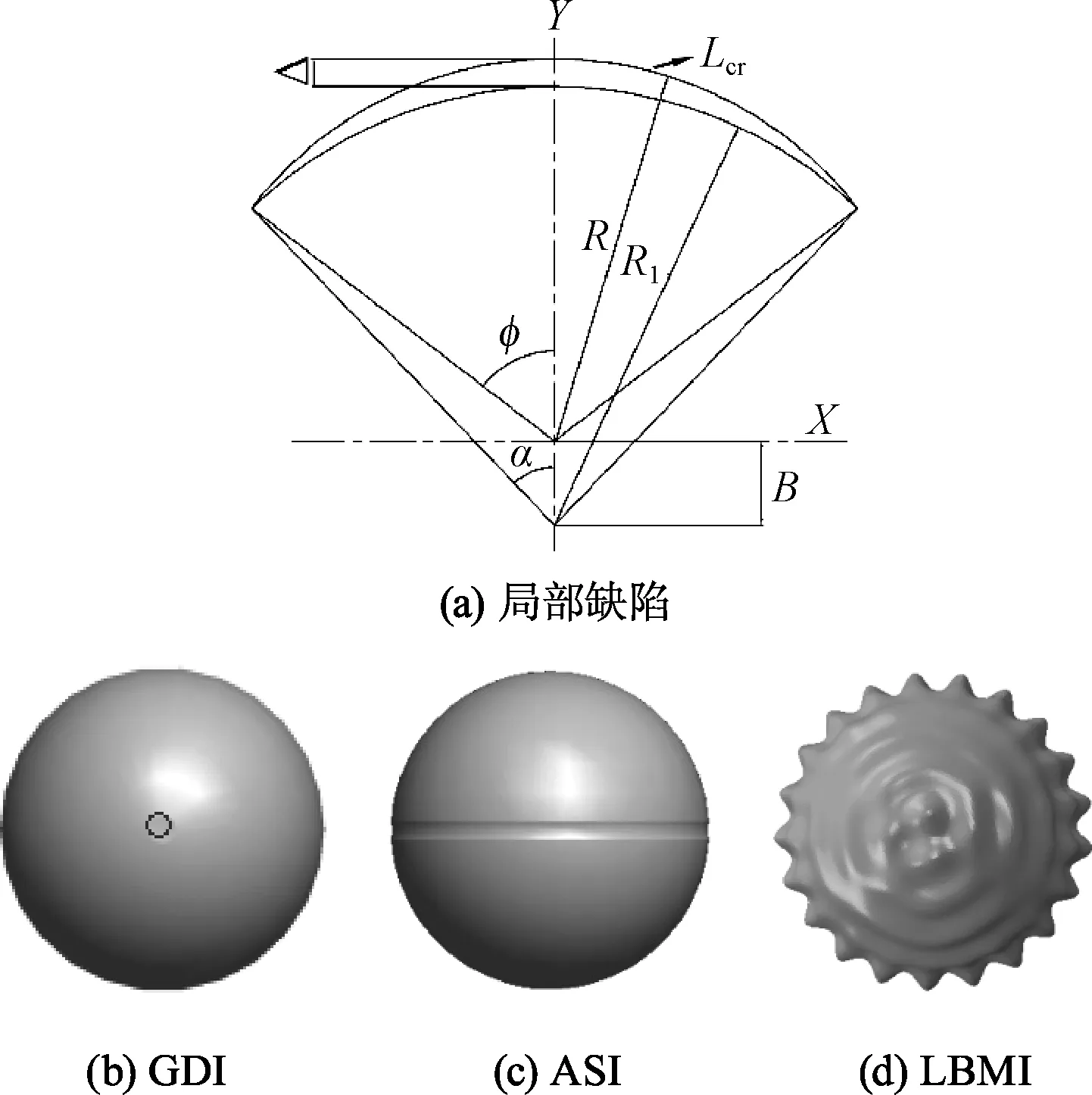
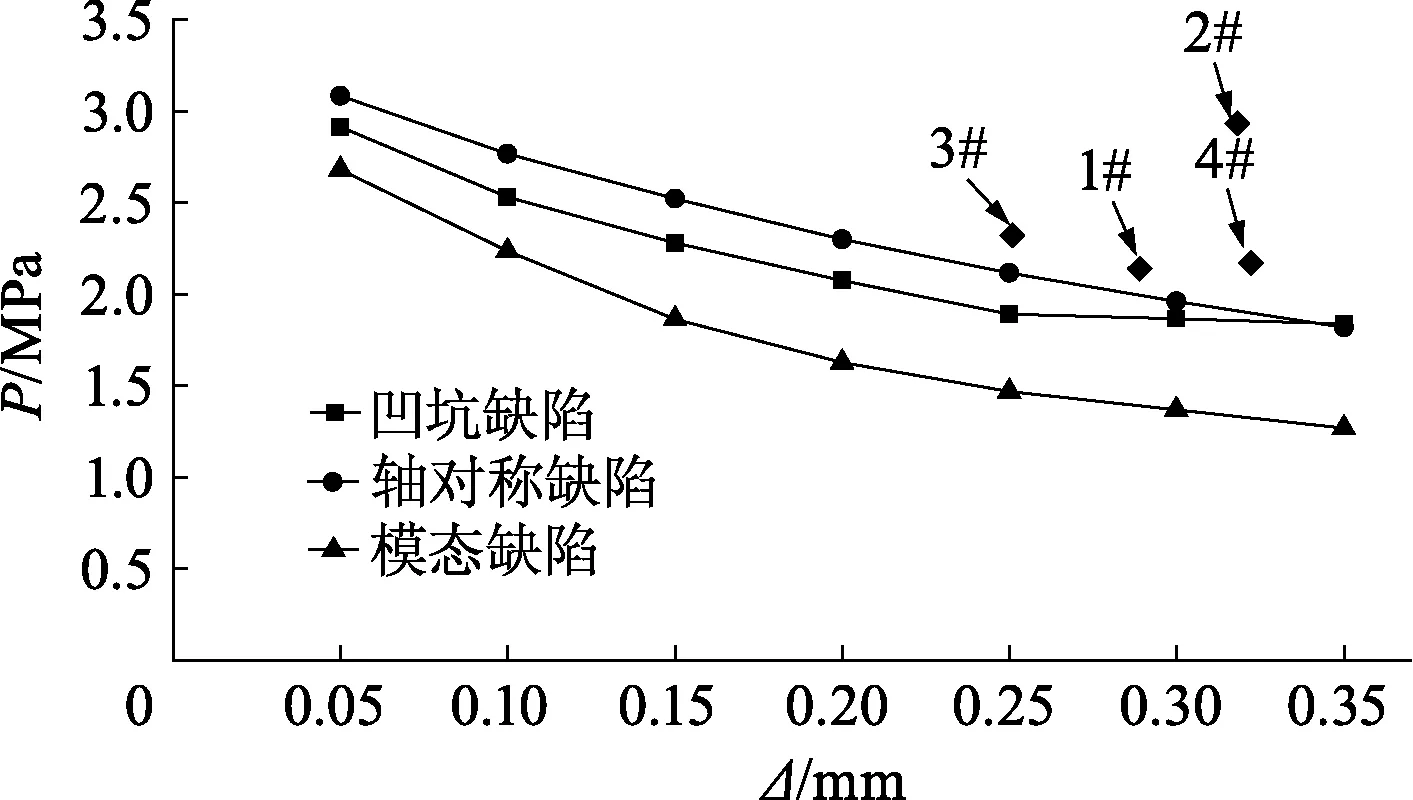
此外,把三维扫描得到的球壳模型导入三维软件UG,进行表面积与体积的测量.根据球度的计算公式求得球度S(0 S=d/a (5) 式中:d为同体积球体之表面积;a为球体之实际表面积. 球壳的圆度与球度如表1,4个试验球壳的平均半径Rave在48.65 mm左右,圆度在0.25~0.33 mm之间,圆度分别约为半径的0.59%、0.65%、0.52%、0.66%.圆度将用于对比缺陷球壳模型的缺陷幅值,以建立等效的缺陷球壳模型;球度是指壳体的形状与球体相似的程度,S值越接近1,其与球体更为接近,可见试验球壳都是十分理想的球体. 表1 球壳的圆度和球度Table 1 Out-of-roundness and sphericity of spherical shells 无损测厚试验和三维扫描试验之后,进行静水压力试验,以获得球壳的屈曲载荷和破坏模式.由于试验对象为不锈钢空心球,在压力舱中的浮力比自身重力高出约4 N,若直接进行压力试验,压力舱盖会对球壳顶部产生扰动力,影响其屈曲特性.为此,使用材质柔软的泡沫网兜包住球壳,并在下端挂上重物,保证球壳悬浮在水中,如图5. 图5 静水压力试验Fig.5 Hydrostatic test 水压试验结果分别列于表2.图6为试验过程中水压舱内水压变化曲线.由图6可见,水压P从0逐渐增至峰值后急剧下降.水压急剧下降是球壳在屈曲时发生大面积凹坑失稳所造成的.因此,水压曲线的峰值就是球壳的压溃压力,且4个试验球壳都符合这一现象.球壳的压溃压力值列于表2;4个球壳的水压值在2~3 MPa之间,可见水压试验的可重复性及可靠性.球壳破坏形式如图7,4个球壳都以凹坑形式破坏,凹坑变形幅度增大引起焊缝裂开,致使球壳破坏进水. 图6 水压曲线Fig.6 Curves of water pressure 图7 球壳破坏形式Fig.7 Collapse shapes of spherical shells 由Zoelly提出的经典屈曲理论用于预测球壳的弹性屈曲值Pcr,如公式6.此公式广泛用于海洋及航空领域,也是船级社球形耐压壳稳定性设计规范的理论基础. (6) 式中:E、μ分别为材料的弹性模量和泊松比;t、R分别为球壳的壁厚和半径. 表2列出了4个试验球壳的经典屈曲理论公式计算结果,根据Zoelly公式计算的屈曲临界压力在10~12 MPa,而试验得到的球壳压溃压力在2~3 MPa,约占理论计算的1/6~1/3.可见Zolley公式结果偏大,与球壳实际破坏压力有较大差距.这是由于Zolley公式无法考虑球壳的非线性和缺陷等因素,故与实际结果有明显不同. 表2 理论与试验结果Table 2 Theoretical and experimental results MPa 为了与水压试验结果进行比较,文中建立了真实的球壳模型,并采用ABAQUS软件的胡长法进行非线性数值分析.首先,将三维扫描得到的球壳表面结构作为球壳模型的壳面,由ANSA软件进行网格划分,4个球壳的网格单元类型为壳单元S4,单元数分别为30 378、32 493、32 079、31 553.为了消除模型的刚性位移,边界条件以3个点限制其六个方向自由度,即在x和z轴相隔90°的位置上取3个节点分别限制2个方向自由度,如图8.结果显示各点约束反力接近0,说明所施加的约束合理,仅限制了模型的刚体位移.并采用弧长法进行求解计算,初始弧长为0.1,最大弧长为0.5.最后,运用ABAQUS/Viewer进行后处理. 图8 网格划分和边界条件Fig.8 Mesh and boundary conditions 有限元计算结果如表3.从球壳的临界屈曲模式可见,球壳焊缝旁边出现最大位移变化点;并且球壳后屈曲模式,即球壳最终失稳模式,展现出凹坑状的凹陷形式.上述结果与球壳的水压试验结果基本一致,4个试验球壳的压溃形式为焊缝周边出现凹坑凹陷导致焊缝裂开,由此确认非线性有限元数值分析可以准确预测球壳屈曲失稳模式.由计算压力和试验压力比较可得,两者的误差百分比分别为3.1%、9.5%、7.5%、4.3%,可见通过有限元数值计算的临界屈曲载荷十分接近试验压力.因此,这一方面验证了非线性数值分析可准确预测球壳的极限承载能力;另一方面也表明考虑真实几何缺陷的数值分析可以预测球壳的失稳区域和失稳形式.故而在耐压舱的设计阶段采用非线性的数值分析方法是可靠的,可有效缩短设计周期及减少设计费用. 表3 球壳屈曲载荷和屈曲模式Table 3 Buckling loads and buckling modes of spherical shells 分别采用凹坑缺陷(GDI)、轴对称缺陷(ASI)与一阶模态缺陷(LBMI)对球壳屈曲特性进行仿真研究,缺陷形式如图9.首先,根据试验得到的平均数据,建立直径为97.3 mm、厚度为0.34 mm理想球壳数值模型,对该模型进行线性屈曲计算,求出一阶屈曲失稳模式,作为一阶模态缺陷;其次,将3类等效几何缺陷作为初始缺陷,引入到理想球壳数值模型中,考虑材料和几何非线性,采用弧长法开展屈曲特性分析.其中,凹坑缺陷和轴对称缺陷形式以图9(a)所示的缺陷截面,分别按Y与X轴旋转而成.单元类型、载荷、边界条件与求解方法前处理方法一致,3种缺陷球壳模型的网格单元数分别为29 876、30 015、29 698.由文献[12]可知:对于局部缺陷(即凹坑缺陷与轴对称缺陷),缺陷范围φ可由临界弧长Lcr确定,故确定缺陷范围φ,而变化缺陷幅值进行数值计算.3种缺陷球壳的缺陷幅值Δ分别取0.05、0.1、0.15、0.2、0.25、0.3、0.35 mm.局部缺陷球壳模型仿真时,需要解决球心距B变化的问题,球心距B由式(7~9)计算而得. 图9 缺陷形状Fig.9 Imperfect shapes α=2arctan((R(1-cosφ)±Δ)/Rsinφ) (7) R1=Rsinφ/sinα (8) (9) 式中:Δ为缺陷幅值;R为完美球壳半径;R1为局部缺陷处半径;φ为缺陷处对应于完美球壳半径的圆心角之半,即缺陷范围;α为缺陷处对应于局部半径的圆心角之半. 不同初始缺陷球壳的屈曲模式如表4,临界屈曲状态下,3种缺陷球壳都在初始缺陷处出现最大的位移变化;后屈曲模式时,球壳都呈现凹坑凹陷的形式.图10为球壳数值结果与试验结果的比较,在3种缺陷形式中,模态缺陷球壳的计算压力最小,故模态缺陷为最危险的缺陷形式.设计时若以该缺陷为依据将得到最厚的壳体壁厚,因此称为最保守的设计.轴对称缺陷球壳的计算压力最大,若采用该值作为设计依据,将对应最不保守的设计.同时,随着缺陷幅值的逐渐增大,3种缺陷球壳的计算压力值越来越小.此外,4个球壳的真实缺陷幅值在0.25~0.33 mm之间,此时,球壳的试验压力结果都位于3种缺陷球壳的计算压力上方,1#、3#与4#球壳的试验压力与轴对称缺陷球壳的计算压力值十分接近;而2#小球的试验压力与数值计算结果相差较大,主要是由于2#小球的壳厚大于其他小球,也与球壳加工过程存在的各种制造精度问题有关.因此,由上述结果可得,轴对称等效缺陷球壳的有限元分析结果可预测耐压球壳的极限承载力. 图10 缺陷球壳数值结果与试验结果的比较Fig.10 Comparison between numerical and experimental results of spherical shells (1) 解析法求出的球壳屈曲载荷与试验结果相差非常大,而基于弧长法的数值计算结果与试验结果具有良好一致性,考虑真实形状和厚度的非线性有限元分析可用于分析真实球壳的屈曲特性. (2) 通过3种等效初始几何缺陷的非线性有限元分析表明,模态缺陷条件下球壳屈曲计算结果最为保守,其次是凹坑缺陷,轴对称缺陷计算结果与试验结果最为接近,可有效预测球壳的极限承载力.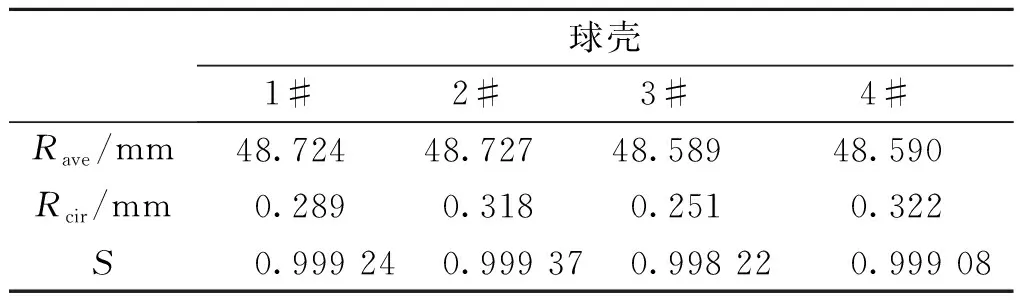


2 理论计算及数值分析
2.1 理论计算
2.2 数值模拟

3 等效缺陷球壳对比分析
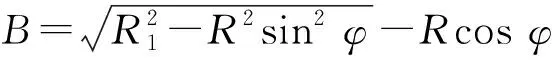
4 结论

