考虑摩擦的滚珠丝杠式惯容器惯质系数修正方法
郭俊华,温华兵,刘 悦,李 阳
(江苏科技大学 能源与动力工程学院,镇江 212003)
随着在船舶动力装置中广泛应用高速大功率柴油机,动力装置的振动与噪声已经成为突出问题[1],而现有的动力装置隔振还是通过传统的质量-弹簧-阻尼(MCK)隔振系统实现.文献[2]首先提出惯容器的概念,并给出两种最基本的形式,即滚珠丝杠惯容器和齿轮齿条式惯容器.目前,惯容器已经在车辆[3-4]、船用手术台[5]、建筑[6]、动力吸振器[7-8]、电缆[9]等领域得到了广泛应用.惯容器的出现打破了传统的MCK隔振系统,开创了惯容器-弹簧-阻尼(inerter-spring-damper,ISD)隔振系统.随后,国际上对惯容器及其应用开展了深入研究,分析非线性因素对惯容器的影响.文献[10]考虑到惯容器结构中存在的间隙、摩擦和弹性力,建立惯容器非线性力学模型,研究非线性因素对ISD悬架计算过程的影响.文献[11]对滚珠丝杠式惯容器和齿轮齿条式惯容器进行台架实验,发现机械式惯容器中存在的背隙和弹性力对它们的力学性能有着直接的影响.文献[12]分析含惯容器的多层隔振系统动态性能.文献[13-14]基于对滚珠丝杠式惯容器中摩擦、间隙以及丝杠弹性力的考虑,建立惯容器非线性模型并进行力学性能试验,得到便于参数识别的惯容器力学模型结构,并且提出一种新型的液压惯容器,分析非线性对其的影响.
上述文献表明,惯容器的非线性因素对惯容器的动力学性能和ISD悬架的减振性能都有较大的影响.随着惯容器的应用日益广泛,惯质系数作为惯容器的固有属性,对其计算的准确性显得尤为重要,尤其是在低频、精密的隔振场所.因此,在工程应用中需要进一步研究非线性因素的惯容器惯质系数的计算方法.文中分析滚珠与滚道之间的差动速度,从而得到摩擦效率,推得滚珠丝杠式惯容器的摩擦惯质系数计算方法,分析滚珠丝杠副的参数对惯质系数的影响.
1 接触点的滑动差动速度
1.1 坐标系的建立
滚珠丝杠式惯容器如图1,为了对惯容器中滚珠丝杠副进行动力学分析,建立了如图2坐标系(O-X,Y,Z),其中Z轴与丝杠的中心轴重合;此外,基于滚珠中心的运动轨迹,建立了Frenet标架(o′-t,n,b),用于研究滚珠与滚道接触区域的滑动现象.
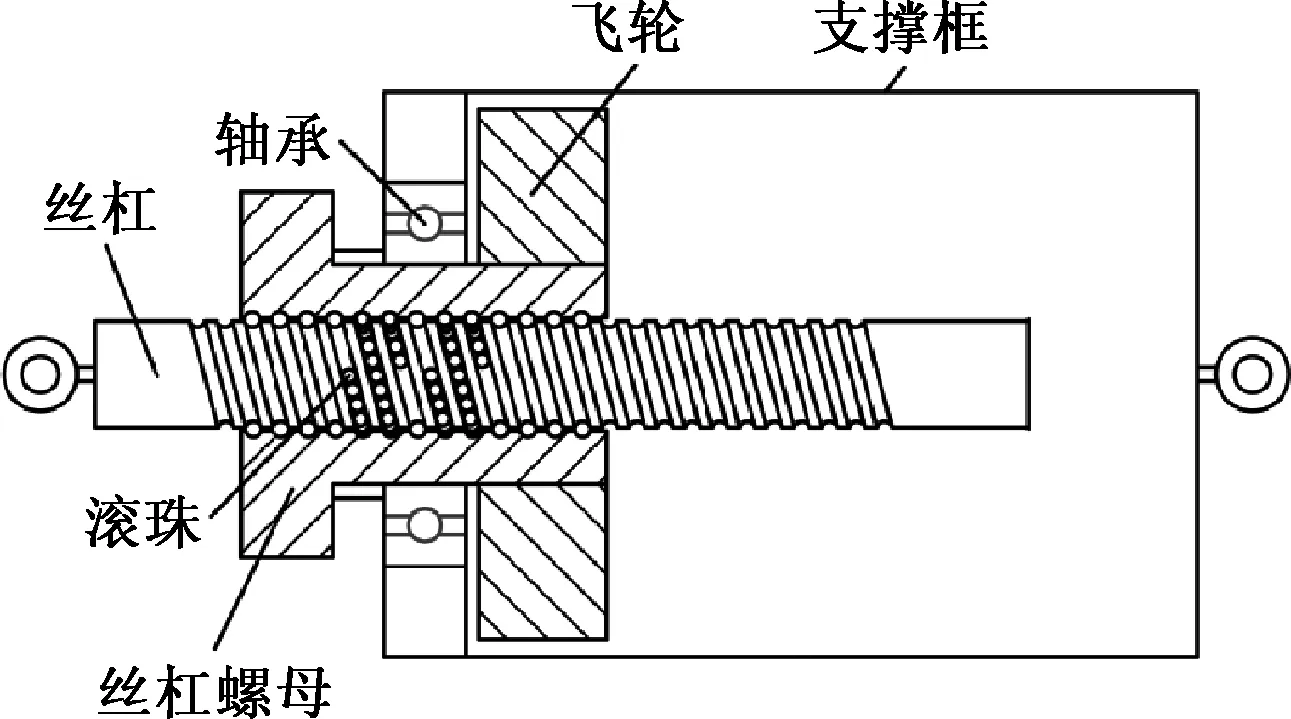
图1 滚珠丝杠式惯容器Fig.1 Model of ball-screw inerter
设世界坐标系的基向量为:W=(i,j,l)T,Frenet标架的基向量为:F=(t,n,b)T,根据文献[15]可知世界坐标系和Frenet标架之间的转化关系.
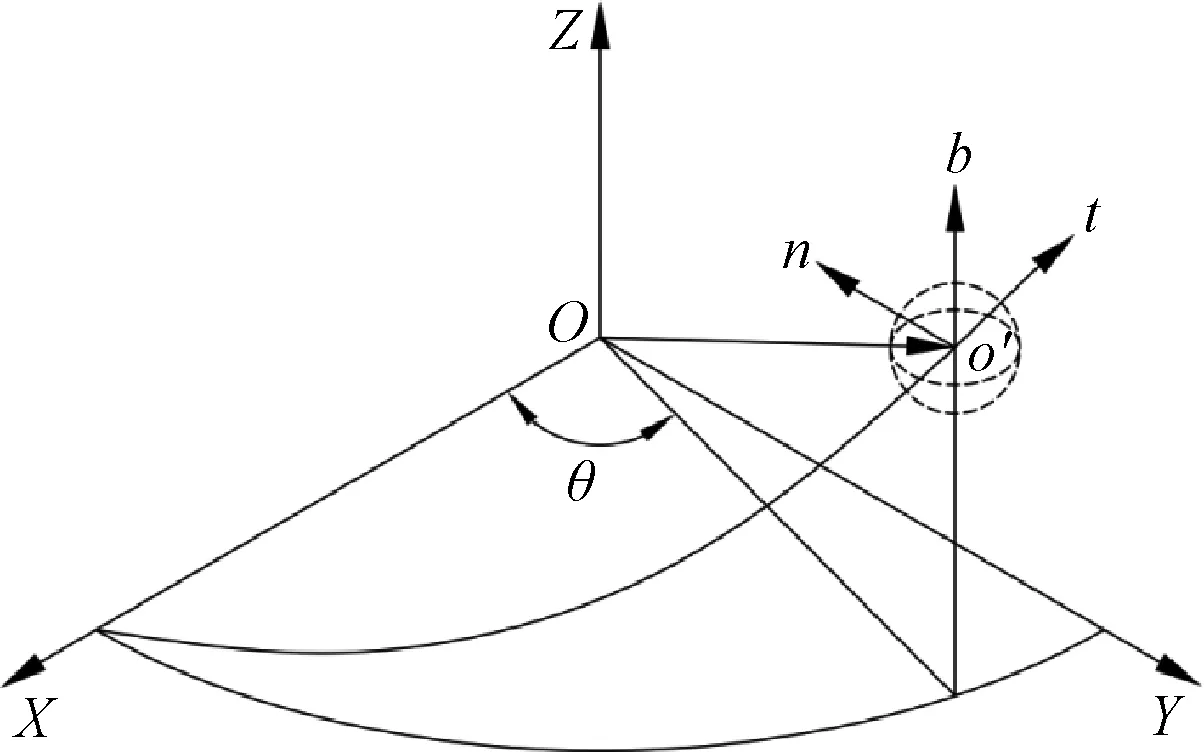
图2 坐标系的建立Fig.2 Establishment of coordinate system
根据图2,将滚珠中心的螺旋轨迹方程表示为:
R={ro·cosθ,ro·sinθ,ro·θ·tanα}W
(1)
1.2 滚珠上接触点的运动
滚珠接触如图3,在Frenet标架中,滚珠与丝杠螺母的接触点为A,滚珠与丝杠的接触点为B,定义滚珠与丝杠螺母的接触角为βA,滚珠与丝杠的接触角为βB.
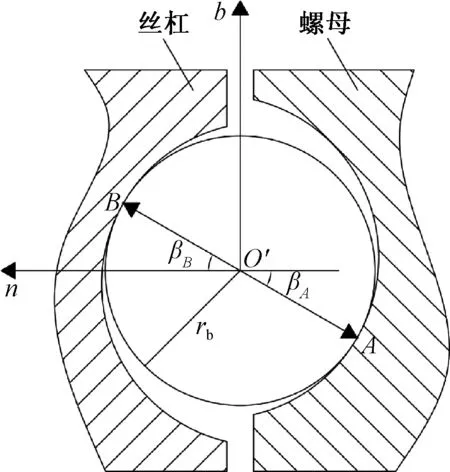
图3 滚珠接触Fig.3 Ball contact
将式(1)转化到Frenet标架中,求导可得:
(2)
设滚珠在Frenet标架中的瞬时自转角速度为:ωball={ωt,ωn,ωb}F,则滚珠在接触点A、B的瞬时速度分别表示为:
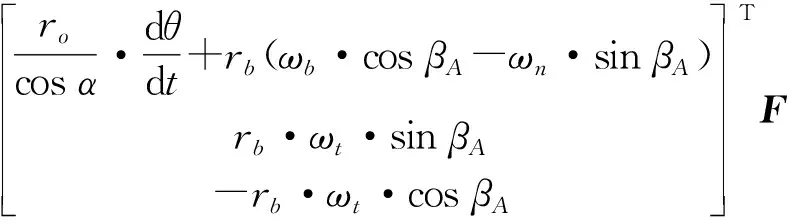
(3)
(4)
式中:O′A={0,-rb·cosβA-rb·sinβA}F,O′B={0,rb·cosβB,rb·sinβB}F,rb为滚珠半径.
1.3 丝杠螺母侧接触点的运动
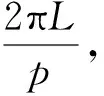
(5)
1.4 丝杠侧接触点的运动
在世界坐标系中,接触点B的速度为:
(6)
将式(6)转化到Frenet标架中去,得到:
(7)
1.5 接触点的差动速度
根据接触点A在滚珠上的速度VA,ball和丝杠螺母侧的速度VA,nut,得到接触点A的差动速度为:
VA=VA,ball-VA,nut=
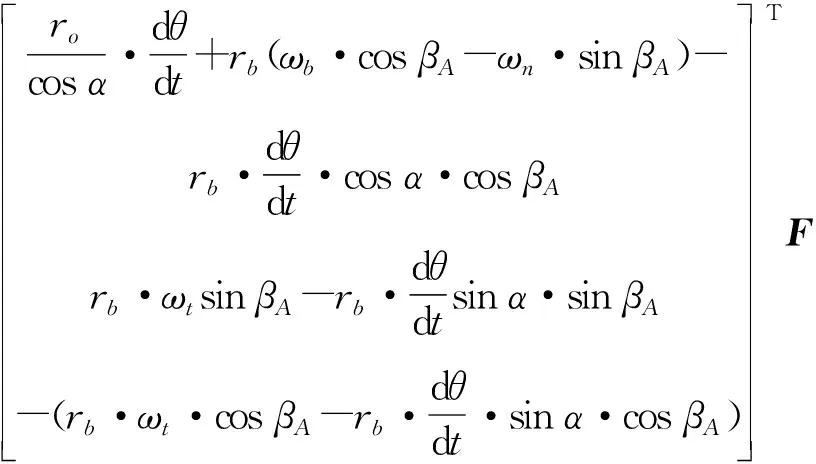
(8)
同理可得接触点B的差动速度为:
VB,ball-VB,screw=
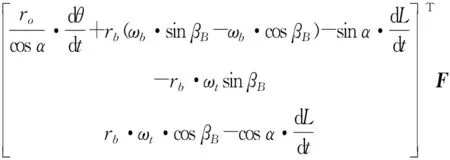
(9)
滚珠运动如图4,由于滚珠丝杠副中接触角的存在,滚珠在沿滚珠中心轨迹滚动的同时,会产生绕接触点公法线的自旋滑动现象.
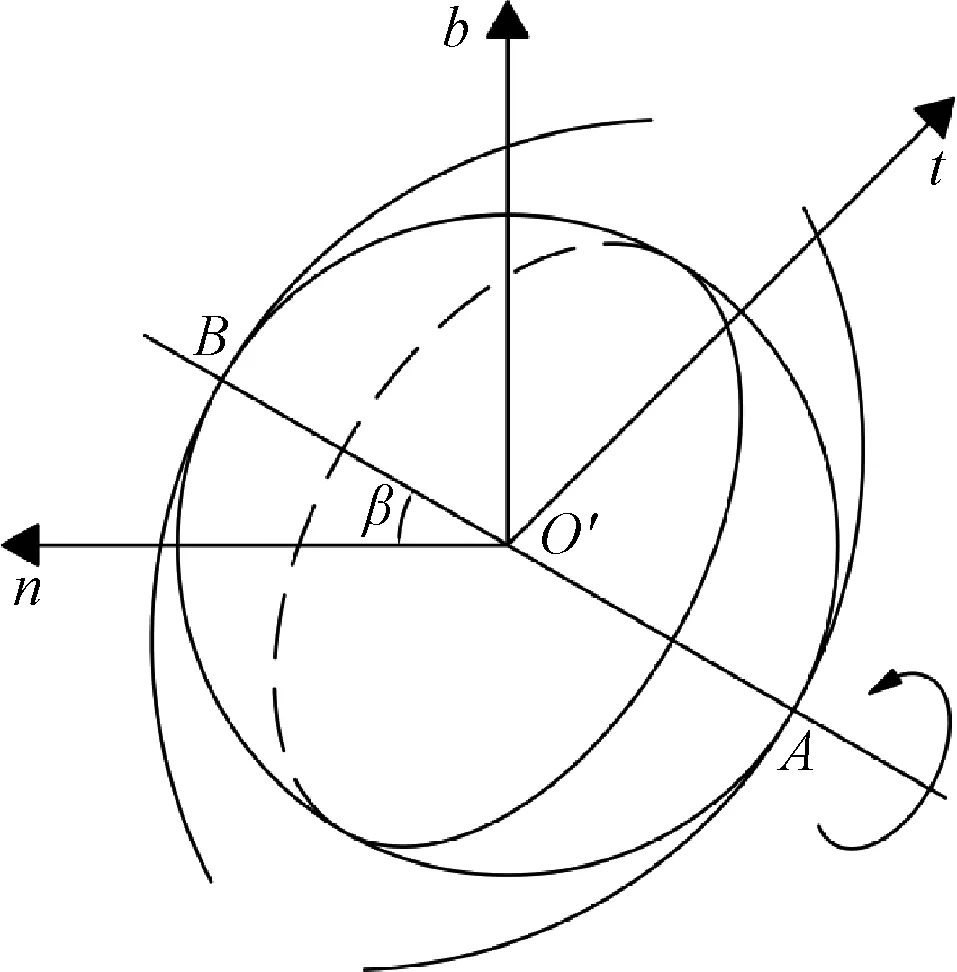
图4 滚珠运动Fig.4 Ball movement
由于惯容器一般应用于中、低频的工程减振系统中,并且接触点A和B的公法线都处于法平面b-n内,所以可以近似认为βA=βB=β,则根据平面向量几何的知识可知:O′A∥O′B,即两个接触点的公法线重合,假设滚珠围绕公法线旋转的角速度大小为ωo′,则可以得到以下方程组:
(10)
将方程组(10)代入VA和VB的表达式中,并且转化成绕接触点公法线的角速度,得到:
(11)
(12)
2 摩擦效率及摩擦惯质系数
根据文献[16]可得到两点的摩擦力矩MAF和MBF,总的摩擦功率可以表示为:
Pf=MAF·ωA+MBF·ωB
(13)
此外,激励功率可以表示为:
(14)
定义摩擦消耗的能量占总激励的百分比为摩擦效率:
(15)
若不考虑非线性因素,根据文献[2],滚珠丝杠式惯容器的理想线性惯质系数计算方法为:
(16)
式中:J为飞轮和螺母的总转动惯量.
根据前面推导得到的摩擦效率,在滚珠丝杠式惯容器的理想线性惯质系数基础上引入非线性因素,最终推导出摩擦惯质系数计算方法为:
(17)
3 摩擦惯质系数实验验证及参数评估
3.1 实验验证
图5为滚珠丝杠式惯容器,为了验证所推导摩擦惯质系数及其计算方法的正确性,对MTS振动实验台上开展惯质系数测试实验.对滚珠丝杠惯容器加载不同频率的正弦激励,加载频率范围为1~10 Hz,每1 Hz测试一次.此外,滚珠丝杠副的公称半径ro=12.5 mm,导程p=10 mm,滚珠与滚道的接触角β=45°,滚珠数量为52.惯质系数实验结果如表1.

图5 实验装置Fig.5 Experimental device表1 实验点记录Table 1 Experimental results of inertance
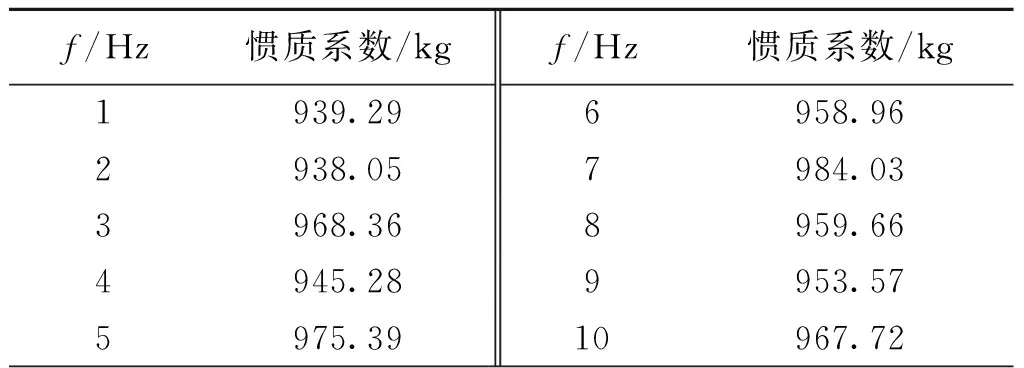
f/Hz惯质系数/kgf/Hz惯质系数/kg1939.292938.053968.364945.285975.396958.967984.038959.669953.5710967.72
利用MTALAB对实验点进行拟合,并且将实验拟合曲线与摩擦惯质系数、理想线性惯质系数作比较,得到图6.实验结果表明,文中的摩擦惯质系数结果略大于实验拟合结果.在频率小于10 Hz时,理想线性惯质系数与实验惯质系数误差较大,在一些要求较高的隔振系统中,使用理想线性惯质系数将引入较大误差.然而,在频率小于10 Hz时,摩擦惯质系数与实验惯质系数误差小于5.0%,尤其是频率大于2 Hz时,摩擦惯质系数与实验惯质系数误差小于2.0%.显然,相比于理想线性惯质系数,文中推导的摩擦惯质系数在滚珠丝杠式惯容器适用的低频范围内更加精确.
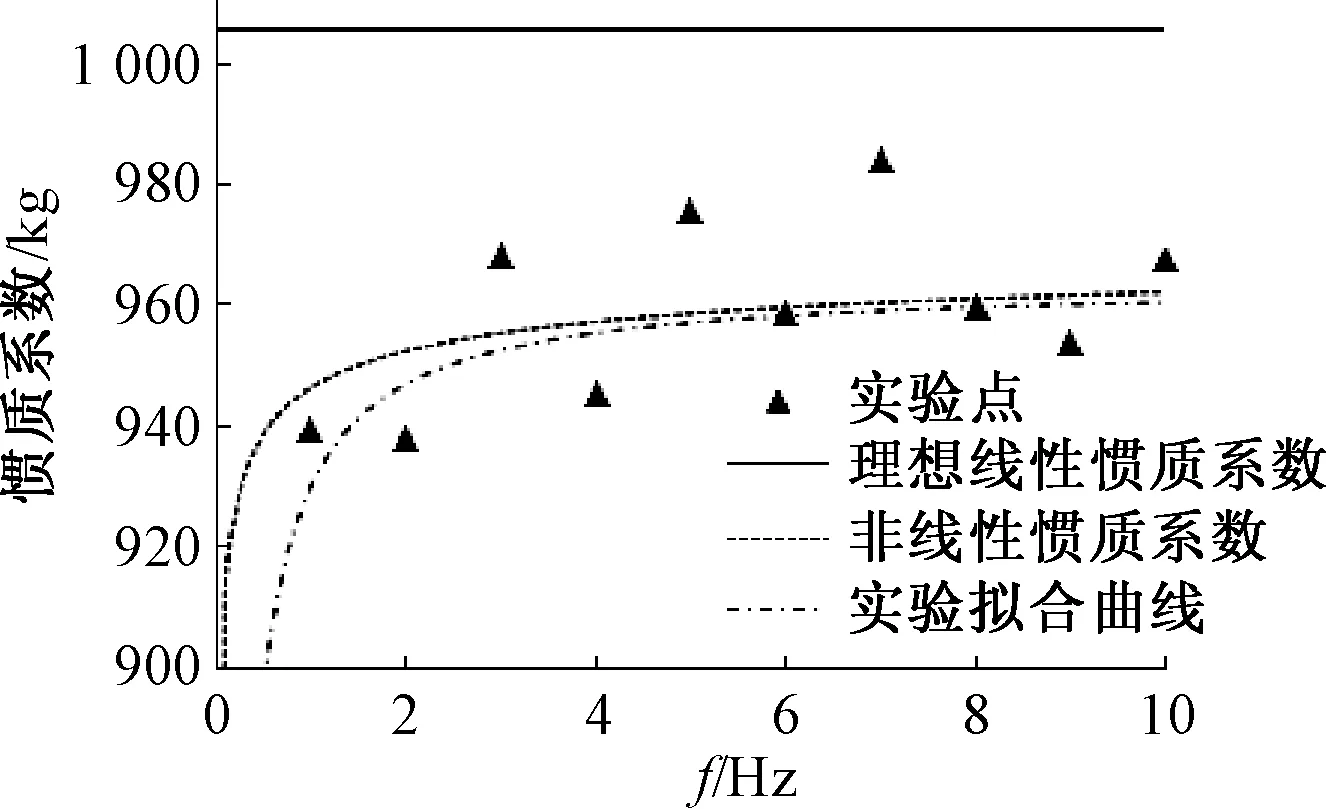
图6 不同方法得到的惯质系数Fig.6 Inertance obtained by different methods
3.2 参数评估
利用文中摩擦惯质系数计算方法,分析滚珠丝杠惯容器的主要参数对摩擦惯质系数的影响.
图7为不同频率下导程、公称半径、滚珠半径、滚珠数量以及接触角对摩擦惯质系数影响的比较,其他参数同前.在相同频率下,导程越小、公称半径越小、滚珠半径越大、滚珠数量越小、接触角越小,惯质系数越大;导程越大、公称半径越大、滚珠半径越小、滚珠数量越大、接触角越大,滚珠丝杠副中的摩擦越严重,摩擦效率越高,从而导致惯质系数越小.此外,在相同导程、相同公称半径、相同滚珠半径、相同滚珠数量以及相同接触角下,频率越大,频率对惯质系数影响越弱.
对比图7中各种因素对惯质系数的影响,在图7(a)和(c)中相同频率下的惯质系数分别变化了50%和15%,而在图7(b、d、e)中相同频率下的惯质系数变化均在5%以内.显然,导程和滚珠半径对惯质系数影响较大,分析其原因,导程和滚珠半径对摩擦效率影响较大,从而导致不同导程和滚珠半径下的惯质系数变化较为敏感.
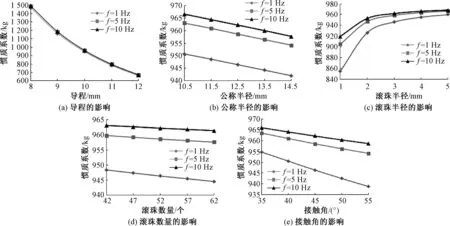
图7 不同因素对惯质系数的影响Fig.7 Influence of different factors on the inertance
4 结论
基于Frenet标架理论与赫兹接触理论,研究滚珠丝杠式摩擦惯质系数的计算方法,通过实验验证该计算方法的准确性,得到如下结论:
(1) 文中所提滚珠丝杠式惯容器摩擦惯质系数在低频时与实际的惯质系数之间的误差小于5%,尤其当频率大于2 Hz时,两者的误差小于2%.所以文中所提滚珠丝杠式惯容器惯质系数较为精确.
(2) 在相同频率下,滚珠丝杠式惯容器的导程越小、公称半径越小、滚珠半径越大、滚珠数量越小、接触角越小,惯质系数越大;此外,在相同几何参数下,频率越大,频率对摩擦惯质系数的影响越弱.

