一类带投资的风险模型的破产概率

沈焰焰

风险理论是保险的基础理论，而破产理论又是风险理论的重要理论.文献［1］提出了赔偿次数是齐次的Poisson过程的模型并成功地求解出破产概率，创造了风险理论的经典模型，奠定了风险理论的基础.文献［2］考虑了Poisson-Geometric过程的赔付次数的模型，解出该模型的破产概率，并求解出赔付额为特定分布下的破产概率的明确表达式.文献［3］提出了带干扰的负风险模型并且考虑赔偿次数符合复合Poisson-Geometric过程，求解出满足该模型的破产概率的积分-微分方程.文献［4］给出赔付次数是复合Poisson-Geometric的模型同时兼顾了投资因素，推导出该模型生存概率满足的积分方程.文献［5］对Poisson过程的再保险风险模型增加了利率因素，求解出破产概率的解析式和Lundberg不等式.本文考虑常利率、风险投资和通胀因素下，保费和赔付均满足复合Poisson-Geometric过程的新模型.

1 模型的建立

设保险公司的盈余过程为

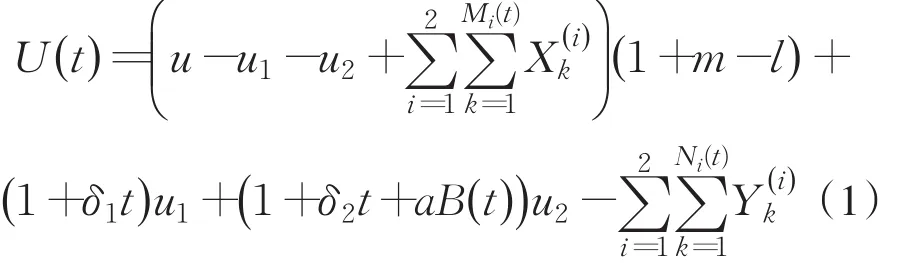
其中，U(t)表示保险公司截止到t时刻的盈余资金；u表示保险公司初始经营的准备资金；u1表示用于投资具有固定收益的资金，u2表示用于高风险高收益投资的资金，m为常利率，l为通货膨胀率，δ1为u1单位时间内投资回报率；δ2为u2单位时间内投资回报率，表示保险公司的第i个险种收取的第k份保单费为保险公司第i个险种赔付的第k次赔偿金额；Mi(t)(i=1，2)表示保险公司的第i个险种截止到t时刻保费收取的次数的总和；Ni(t)(i=1，2)表示保险公司的第i个险种截止到t时刻赔偿次数的总和；B(t)为标准的布朗运动，a为扰动系数.

假 设1{M(t)，t≥ 0} ，{N(t)，t≥ 0} ，{X(i)，ii，k≥1} ，{Y(i)，Y(i)，k≥1} ，{B，t≥0} 均为相互kt独立的；对于固定的i(i=1，2) ，{X(i)，≥1} ，都为相互独立的同分布.

假设3 令H(t)=δ1tu1+(δ2t+aB(t))u2+为盈利过程.为确保保险公司可以稳定经营，一般要求E(H(t))＞0，即

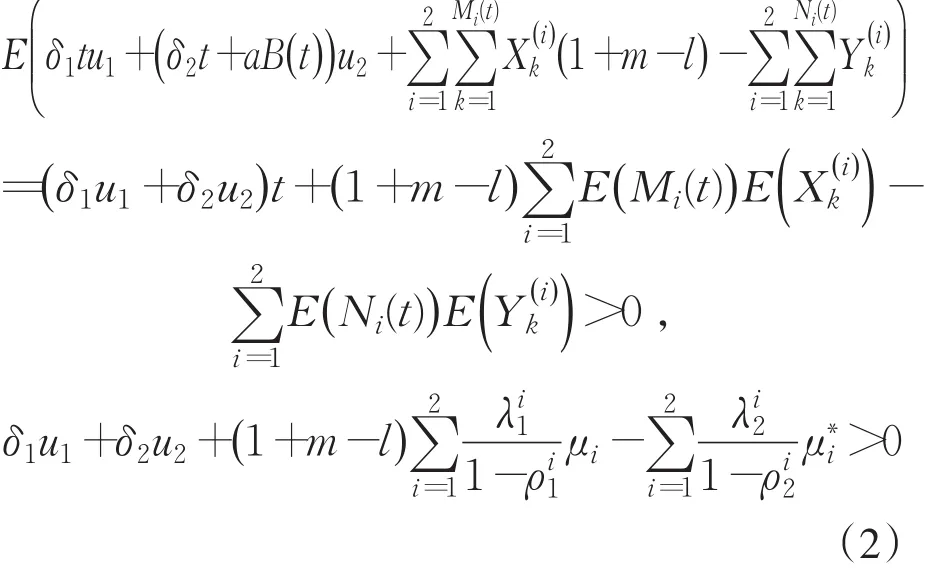
定义1 破产时刻T=inf{t|t≥0，U(t)＜0}.

定义2 最终破产概率ψ(u)=P{T＜∞|U(0)=u}.

2 预备引理

引理1tl→im∞U(t)=∞，a.s..

引理2E(H(t))=(δ1u1+δ2u2)t+

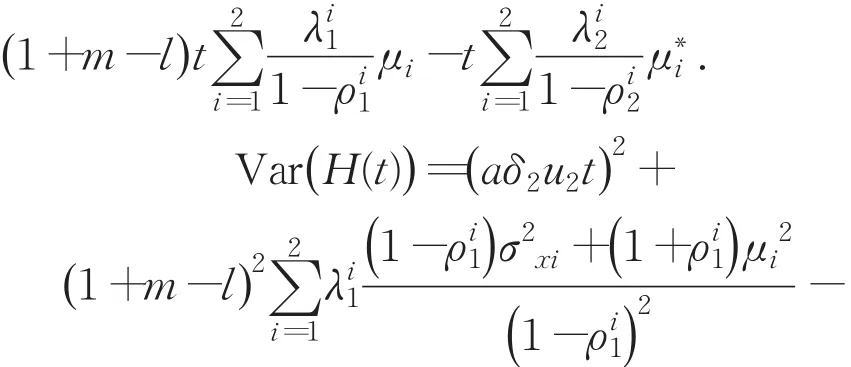
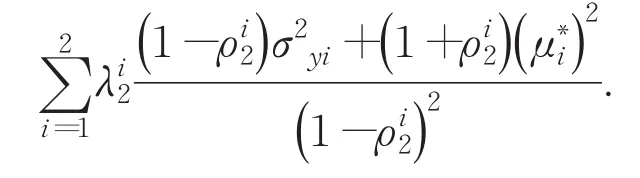
引理3 盈利过程{H(t)，t≥0} 存在函数

引理4 调节方程g(r)=0存在唯一的正解R，称R为调节系数.

3 主要结果

定理1 令F=σ{H(t)，s≤t} ，设X(t)=e-RU(t)，t则{X(t)，t≥0}是秧，其中，R为调节系数.

其中，R为引理3中的调节系数，为ψ(u)的Lundberg上界.

证明 令X(t)=e-RU(t)，根据定理1可知{X(t)，t≥0} 为正秧，则

对于任意固定的t，t∧T为有界停时，有

又有U(T)＜0，e-RU(T)＞1，即上式可变为

定理3 当保费额X(i)，(i=1，2)分别服从参数为βi，(i=1，2)的指数分布，赔偿额Y(i)，(i=1，2)分别服从参数为ai，(i=1，2)的指数分布，则风险模型（1）的最终破产概率的精确表达式为

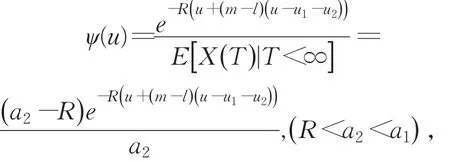
证明 令Z=Y(1)+Y(2)，设概率密度为

fZ(z)，由卷积公式得

设破产时刻T前的盈余为Uˉ，设破产理赔量为Y(1)+Y(2)，设破产时财政赤字量为-U(T)，则有

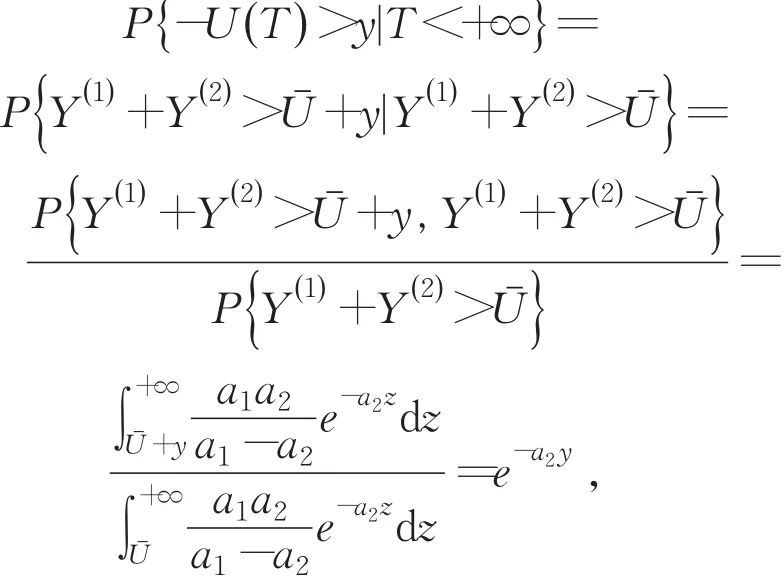
故-U(T) 的概率密度

因为参数为λ指数分布的矩母函数为

4 结论

本文考虑利率、风险投资和通胀等因素下的复合Poisson-Geometric过程的新风险模型，不仅具有独立增量的性质，而且克服了Poisson分布散度偏大的问题，因此本文的风险模型的使用范围比较广也更符合实际情况，同时可以推广到多险种风险模型.