常见向量式几何意义的探析
2018-12-04 07:31浙江省绍兴鲁迅高级中学312000
中学数学研究(江西) 2018年11期
浙江省绍兴鲁迅高级中学 (312000)
何建松
浙江省绍兴鲁迅中学 (312000)
虞关寿
我们在处理向量问题时,往往会采取两条途径,一条是代数途径,利用向量的坐标运算把问题转化为代数问题解决,由于向量坐标运算有一系列的公式与法则,所以这条途径入口较为容易,但需要有较强的运算与变形能力;另一条是几何途径,利用向量的几何功能把问题转化为几何问题解决,由于我们对向量几何性缺乏应有的认识,通过这条途径解决向量问题感到相当费力.如果我们能充分了解一些常见向量式的几何意义,利用这些几何意义去解决相应的问题,往往能起到事半功倍的效果.本文结合近几年的高考与竞赛试题对一些常见的向量式几何意义作一点探析,以备考之用.
一、与距离、投影有关的向量式
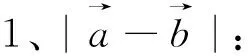
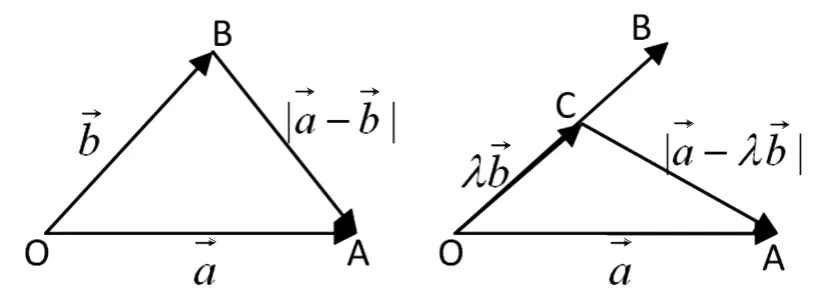
图1 图2
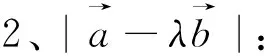
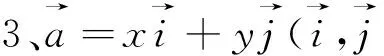
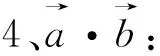
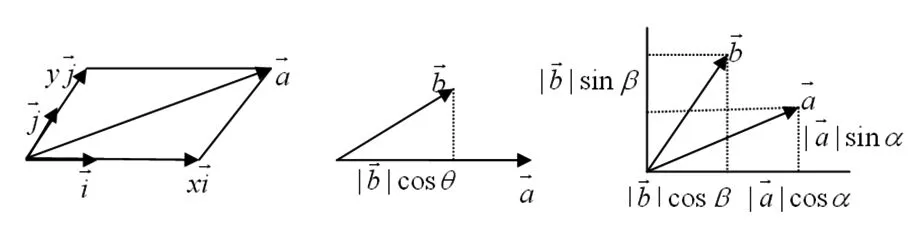
图3 图4 图5
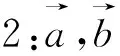
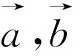
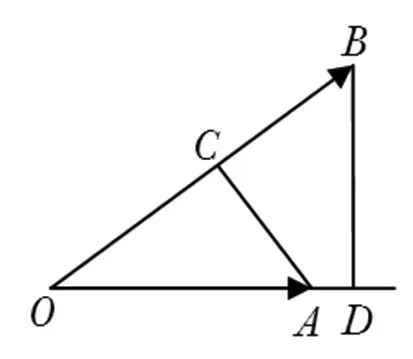
图6
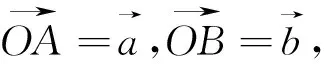
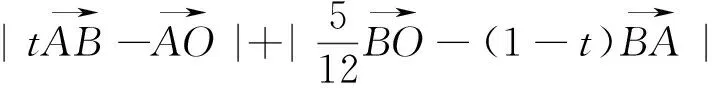
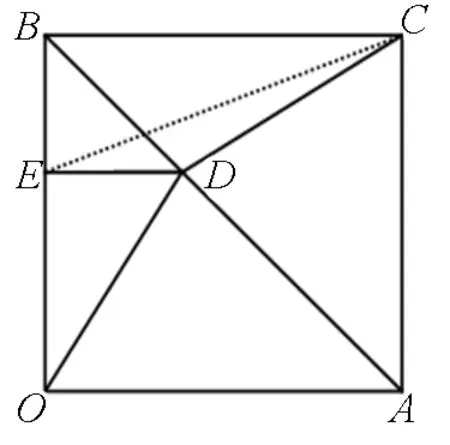
图7
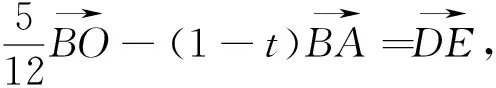
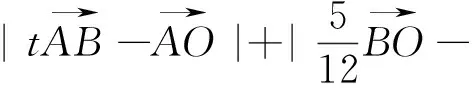
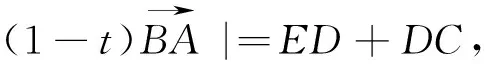
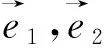
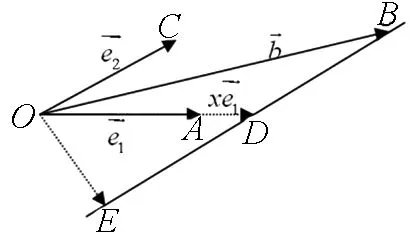
图8
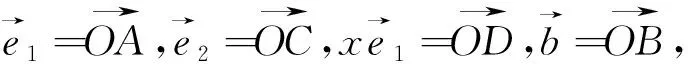
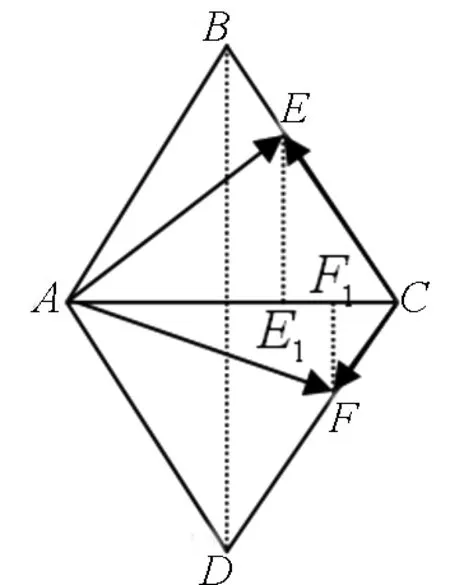
图9
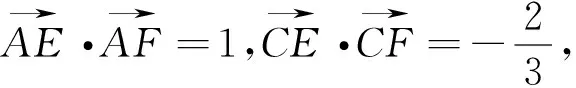
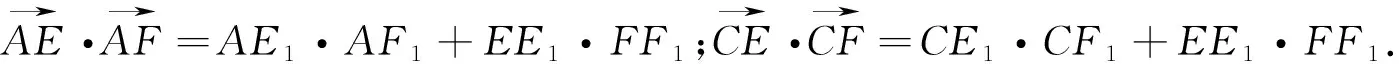
二、与曲线(圆弧)、直线有关的向量式
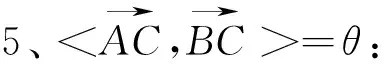
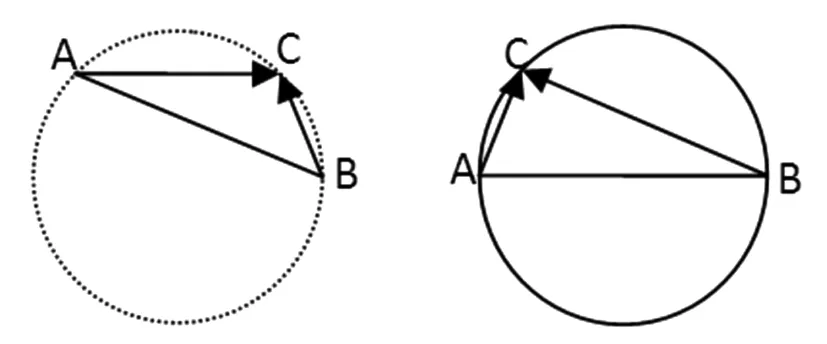
图10 图11
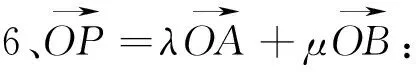
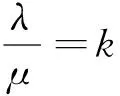
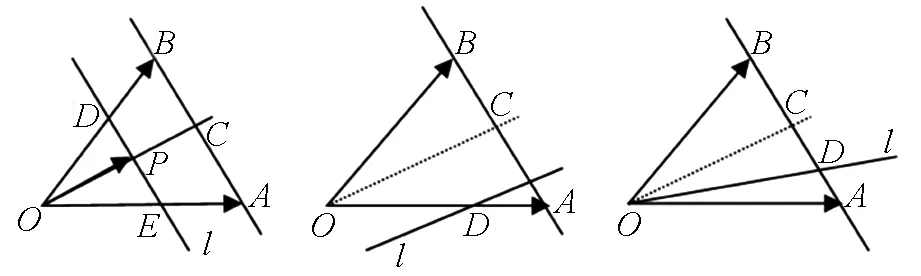
图12 图13 图14
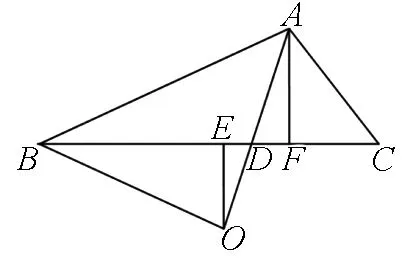
图15
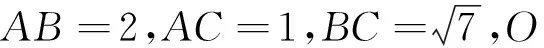
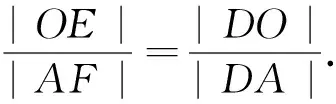
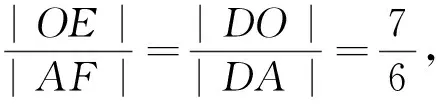
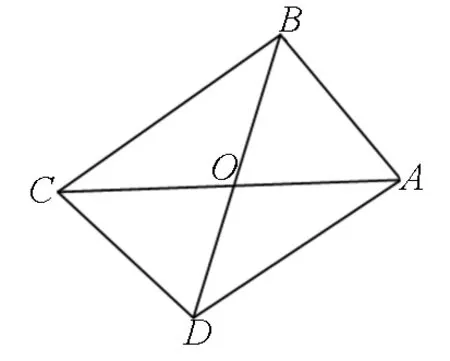
图16
例5 (2013安徽高考)在平面直角坐标系中,O是坐标原点,两定点A,B满足

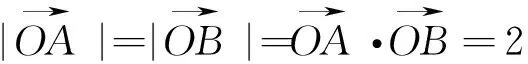
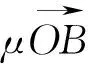
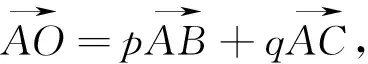
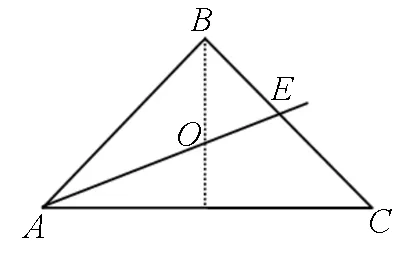
图17
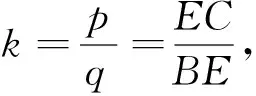
三、与三角形有关的向量式
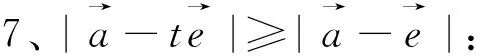
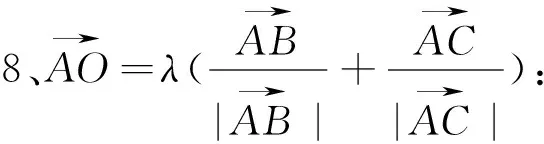
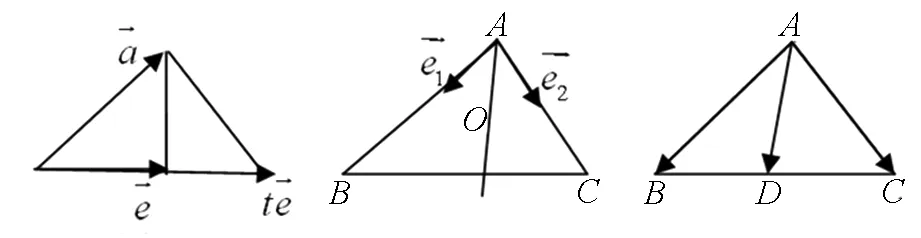
图18 图19 图20
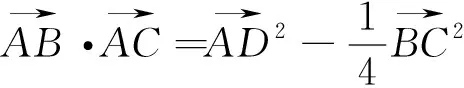
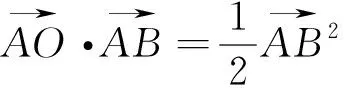
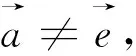
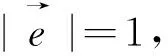
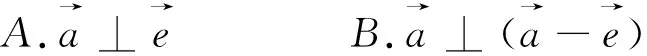
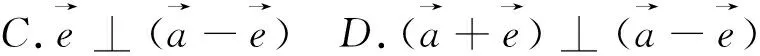
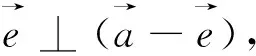
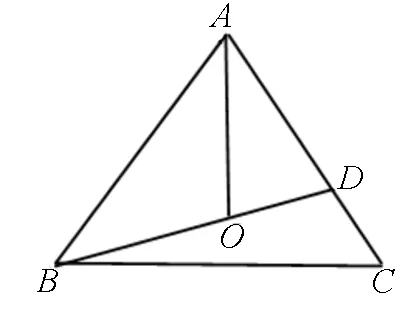
图21
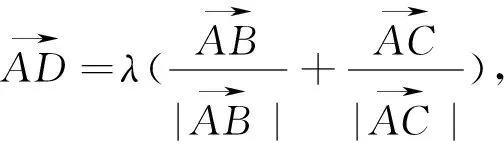
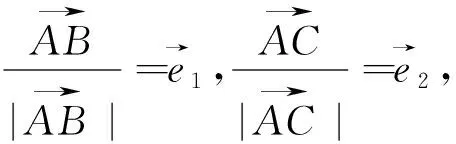
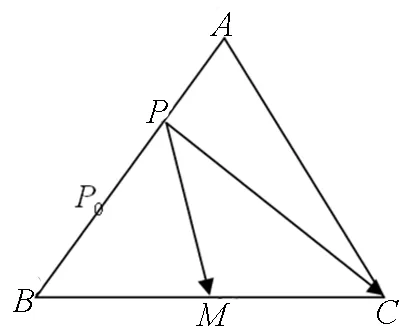
图22
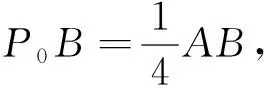
A.∠ABC=90°
B.∠BAC=90°C.AB=ACD.AC=BC
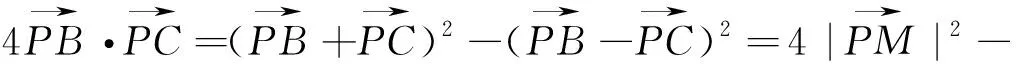
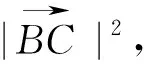
例10 在ΔABC中,D为边AC上一点,AB=AC=6,AD=4,若ΔABC的外心O恰在线段BD上,则BC= .

图23
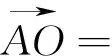
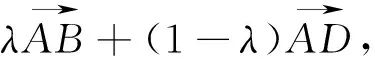
四、与平行四边形有关的向量式
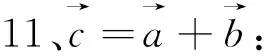
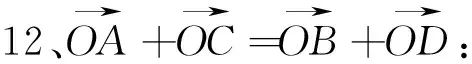
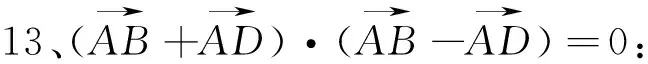
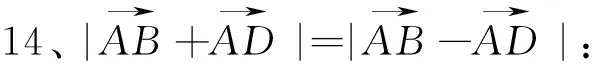
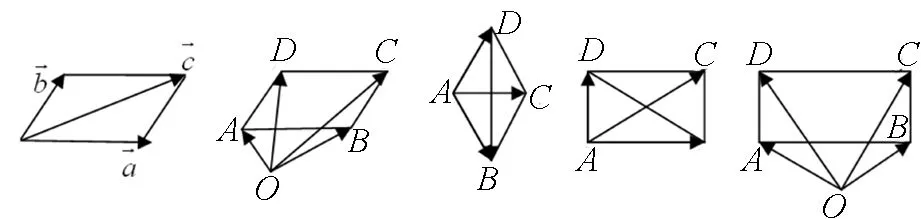
图24 图25 图26 图27 图28
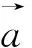
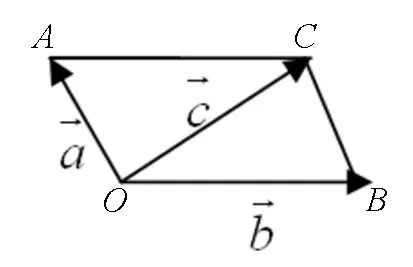
图29
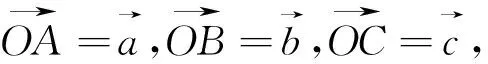
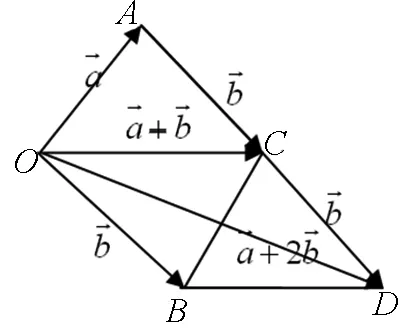
图30
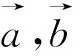
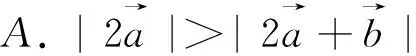

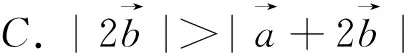
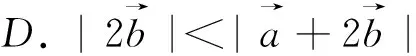
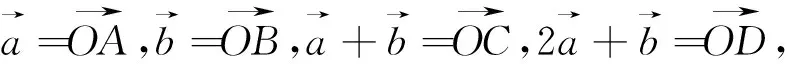
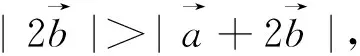
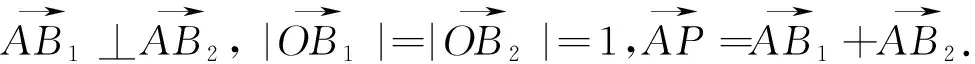
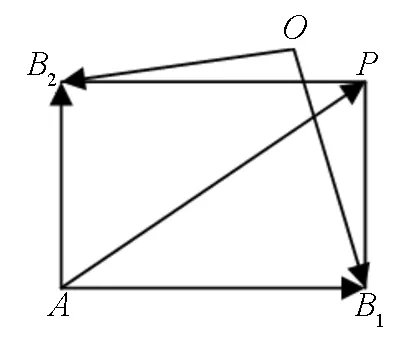
图31
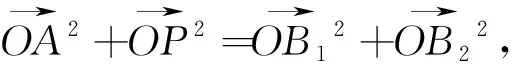
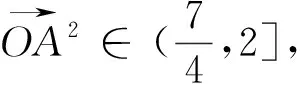
五、与平行六面体有关的空间向量式
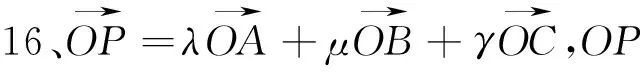
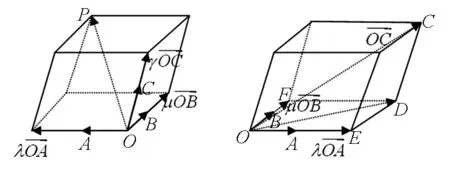
图32 图33
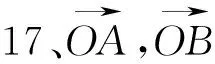
例14 已知平行六面体AC1,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=60°,∠DAA1=60°,则AC1的长为 .
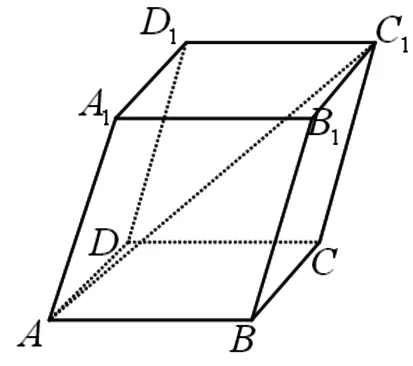
图34
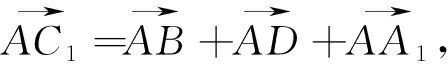
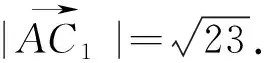
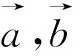
A.5B.7C.12D.13
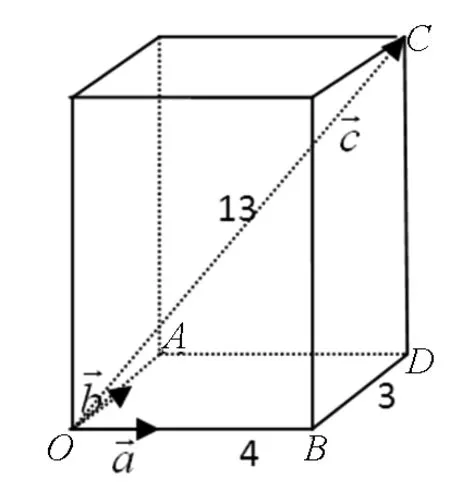
图35
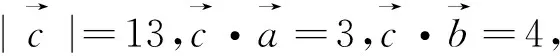
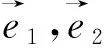
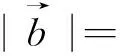
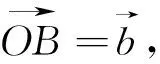
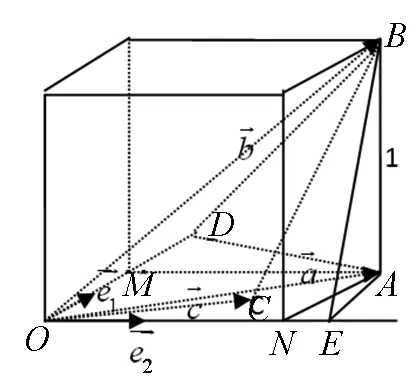
图36
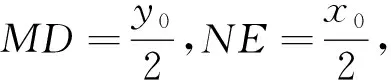
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
食品安全导刊(2021年20期)2021-08-30
数学小灵通(1-2年级)(2021年5期)2021-07-21
河北理科教学研究(2021年4期)2021-04-19
中学生数理化(高中版.高考数学)(2021年1期)2021-03-19
科学(2020年1期)2020-08-24
武术研究(2020年2期)2020-04-21
图书馆建设(2018年8期)2018-08-31
中国市场(2016年12期)2016-05-17
高中生学习·高三版(2016年9期)2016-05-14

