基于前后端图优化的RGB-D三维SLAM

,,,

(1.浙江工业大学 信息工程学院，浙江 杭州 310023;2.南开大学 机器人与信息自动化研究所，天津 300071)

针对处在复杂环境中的机器人，利用自身所携带的视觉传感器获取机器人所在环境的三维空间模型和机器人的运动轨迹，这是视觉SLAM(Simultaneous localization and mapping,即时定位与地图构建)所要完成的工作，也是实现移动机器人任务规划、导航和控制等自主运动的前提之一[1]。近几年，流行的深度摄像机不仅可以获得环境的二维图像信息，还可以准确得到对应环境的深度信息。因此，利用深度摄像机来做视觉SLAM成为研究的热点。现行的RGB-D SLAM算法主要由前端和后端两部分组成[2]。前端部分利用得到的彩色图和深度图计算提取各帧间的空间位置关系，而后端部分对所得到的这些移动机器人位姿进行优化，来减少其中存在的非线性误差。Henry等[3]提出将连续的彩色图间的匹配作为ICP(Iterative closest point迭代最近点)的初始化，通过位置识别提高了回环检测效率，最后采用稀疏捆优化(Sparse bundle adjustment)对移动机器人位姿进行优化。其采用的FAST角点检测方法代替原来的SIFT算法加快了算法的运算速度，但FAST本身缺乏尺度不变性以及旋转不变性，因此鲁棒性较差。Dryanovski等[4]采用Shi-Tomasi角点检测算法得到RGB图像的特征点,运用ICP算法得到当前帧与环境模型的旋转平移矩阵，然后采用卡尔曼滤波方法对环境特征模型进行更新。由于只采用了传统的滤波器方法，因此存在一定的累积误差，精度相对较低。Endres等[5]基于Kinect实现了三维地图的构建，由于采用的SIFT算法很耗时，导致实时性不强；在后端采用了比较简单的闭环检测方法,容易遗漏可能存在的有效闭环。Mur-Artal等[6]提出了一种基于ORB(Oriented brief)的单目视觉SLAM系统，取得了较好的效果。

针对RGB-D SLAM中所存在的上述问题，提出一种基于前后端图优化的RGB-D SLAM算法。主要工作包括将图优化[7]方案应用于SLAM算法的前端和后端[8]，提出一种基于图优化的Bundle Adjustment方法来获取移动机器人相对位姿[9]，既提高了准确性，也能有效提高计算效率。在后端算法中利用基于词袋[10]的回环检测算法检测得到局部回环和全局大回环[11]，利用图优化的方法进行优化来减小累积误差，得到移动机器人位姿的全局最优解。从而得到移动机器人精确的运动轨迹，并构建出准确的三维空间模型[12]。

1 SLAM系统前端

1.1 特征选择

综合考虑计算效率和特征匹配准确度，采用ORB[13]算法对特征点进行检测与描述。ORB具有方向的FAST兴趣点检测和具有旋转不变的BRIEF兴趣点描述子两部分特征提取。

1.2 基于图优化的PnP问题求解

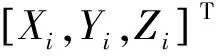
dipi=K(RPi+t)

(1)

根据式(1)计算得到的理论二维像素坐标pi与真实二维像素坐标，可得误差函数ei为

(2)

式(2)的最小化误差T*为

(3)

式中：pi为二维像素坐标；K为相机内参；R为旋转矩阵；t为平移向量；di为深度信息。

采用深度传感器，可以根据深度信息得到匹配点的三维位置。因此，在这里要处理的是已知三维到二维匹配点，求解移动机器人位姿的问题，具体步骤如下：

1) 首先采用EPnP[14]的求解方式求解得到移动机器人位姿的初始值。

2) 然后将当前移动机器人位姿设为图优化中的顶点。

3) 重投影误差作为图优化中的误差项。

4) 利用g2o求解得到移动机器人位姿的最优解。

1.3 提取关键帧

相邻帧之间的距离往往很近，没有明显的差别，将每一帧都添加到地图中，将导致地图的频繁更新，浪费计算时间与空间、降低了效率。为此，采用提取关键帧的方法，当机器人运动超过一定距离时，就增加一个“关键帧”，最后将得到的关键帧拼接起来就得到了三维点云地图。

提取关键帧的具体方法：对于新得到的一帧I，采用1.2节所描述的方法计算I与上一关键帧的相对运动，并判定该运动的大小，若E>Eerror(Eerror为设定的最大运动阈值)，说明运动太大，估计是计算错误，将该帧舍弃。若E

2 SLAM系统后端

2.1 基于DBoW2算法的回环检测简述

在进行全局回环检测前，要先进行局部回环检测，将新加进来的与相邻的前几个关键帧进行匹配，满足相似度标准便可建立局部的小回环，通过这个约束关系来减少当下产生的累计误差。

DBow2(Bags of binary words for fast place recognition in image sequence)是一种高效的回环检测算法，该算法使用Fast算法检测特征点，使用ORB描述子作为特征描述子。

2.2 Bag of Words字典建立

1) 从训练图像中离线抽取特征。

2) 将抽取的特征用k-means++算法聚类，将描述子空间划分成k类。

3) 将划分的每个子空间，继续利用k-means++算法聚类做聚类。

4) 按照上述循环，将描述子建立树形结构，如图1所示。

图1 字典树Fig.1 Vocabulary tree

字典树在建立过程中，每个叶子也就是每个 word 记录了该 word 在所有的训练图像中出现的频率，出现的频率越高，表示这个 word 的区分度越小，因此权重越低。权重的计算公式为

(4)

式中：N为训练图像的数量；ni为word在这些训练图像中出现的次数。

2.3 在线更新字典树

当需要在字典树中插入一幅新图像It，将在图像中提取的描述符按照Hamming距离从字典树的根部开始逐级向下到达叶子节点，计算每个叶子节点即每个word在图像It中出现的频率，计算公式为

(5)

式中：niIt为word在图像中出现的次数；nIt为图像中描述子的总数。在树构建的过程中每个叶子节点存储了inverse index，存储了到达叶子节点的图像It的ID和word在图像It描述vector中第i维的值，即

(6)

对于一幅图像所有的描述子，进行以上操作，可以得到每个word的值，将这些值构成图像的描述向量vt。

2.4 相似度计算

将新得到的关键帧与具有一定数量间隔的所有关键帧逐一径向相似度计算，两幅图相似度计算公式为

(7)

将相似度得分超过一定阈值的先前关键帧都加入到候选队列中。再将候选队列中的每一帧与当前关键帧进行特征匹配，当匹配得到的内点数超过一定阈值时则说明成功检测到闭环。

2.5 图优化的数学建模

采用位姿约束进行SLAM的优化问题建模而不用特征约束，这样做既直观而且减少了很多计算量，增强了算法的实时性。其数学建模为

(8)

式中：x为机器人位姿(包含三维位置与三个角度姿态，采用姿态矩阵来描述)；R为旋转矩阵(正交矩阵)；xt为平移向量，即

xi=Tijxj

(9)

式中Tij为第i帧与第j帧间经过的运动(是通过这两帧的图像匹配所得到的位姿约束)。

将这个优化问题表示成如图2所示的优化图，移动机器人位姿xi作为图2中的节点，帧间约束Tij作为图2中的边。

图2 优化图Fig.2 Optimal graph

由于实际上两个估计值之间存在误差eij，所以存在

eij=(xi-Tijxj)

(10)

由此可推得每条边都存在误差，对这些误差定义一个二范数，并将这些误差相加，就得到了要求解的优化问题的目标函数，即

(11)

对这个优化问题进行求解，其实这就是一个非线性最小二乘问题。设f(x)=eij，将目标函数进行泰勒级数展开，可得到

(12)

于是便可以采用Levenberg-Marquardt算法来求解这个非线性问题，其中该算法可描述为

1) 给定初始值x0, 以级初始化半径u。

2) 对于第k次迭代，求解得

(13)

s.t. ‖DΔxk‖2≤uρ

(14)

3) 计算ρ，得

(15)

6) 如果ρ大于某阈值，认为近似可行，令xk+1=xk+Δxk。

7) 判断算法是否收敛，如果不收敛则返回2)，否则结束。

信赖域内的优化，利用Lagrange乘子转化为无约束，即

(16)

增量方程为

(H+λDTD)Δx=g

(17)

2.6 基于g2o的位姿求解

将前端算法得到的移动机器人位姿作为需要求解的优化变量，将相邻关键帧间的运动约束以及检测到回环的两帧之间的约束作为边加入到图中。由此，便得到了g2o所需的节点(优化变量)和边(误差项)，g2o优化的具体流程如图3所示。

图3 g2o流程图Fig.3 g2o flow diagram

这样便可优化求解得到想要的优化变量即移动机器人的位姿。基于前后端图优化算法可描述为

1) 初始化：读取彩色图与深度图像帧。

2) 提取ORB特征并进行特征匹配。

3) EPnP求解初始位姿x。

4) ifEkey

5) 将当前帧作为关键帧。

6) 利用g2o及式(1～3)优化局部位姿。

7) end if。

8) 由式(4～7)计算得到两帧图像的相似度。

9) ifs(v1,v2)>sw(sw为阈值)。

10) 说明成功检测到闭环。

11) 利用高g2o及式(10～17)优化全局位姿。

12) end if。

根据最优位姿计算得到三维地图及运动轨迹。

3 实验结果与分析

设计了两组实验，其中第一组采用的是Computer vision group提供的数据集Freibury1_floor(简称“floor”)，第二组采用的是自己构建的数据集(简称“自建”)，拍摄的环境是作者的实验室环境,本实验运行在配置为Intel(R) Core(TM) i3 CPU 4 GB RAM 的 Ubuntu 14.04平台上。实验中分别采用前后端图优化的方法，以及在前端只采用opencv中solvePnPRansac函数求解移动机器人位姿的方法对这两组数据进行测试(简称“solvePnPRansac方法”)，基于前后端图优化方法求解floor数据集得到的运动轨迹如图4所示。

图4 图优化解floor数据集轨迹Fig.4 Trajectories of floor data sets based on graph optimization

基于solvePnPRansac方法求解floor数据集得到的实验结果如图5所示。

图5 solvePnPRansac解floor数据集轨迹Fig.5 Trajectories of floor data sets based on solvePnPRansac

分别采用前后端图优化方法和solvePnPRansac方法求解自建数据集得到的轨迹图如图6，7所示。由图4与图5，图6与图7对比可得：采用基于前后端图优化的方法相比于在前端只采用solvePnPRansac方法所得到的轨迹更为准确，而且精度有较大的提高。

图6 图优化解自建数据集轨迹Fig.6 Trajectories of self built data sets based on graph optimization

图7 solvePnPRansac解自建数据集轨迹Fig.7 Trajectories of self built data sets based on solvePnPRansac

采用前后端图优化方法求解floor数据集和自建数据集得到的三维点云地图如图8，9所示。通过这2幅三维点云地图，可以看到以前后端图优化方法为基础拼接得到的三维地图模型也十分精确，进一步表明了前后端图优化方法对于构建三维地图的良好适用性。

图8 图优化解floor数据集地图Fig.8 Map of floor data sets based on graph optimization

图9 图优化解自建数据集地图Fig.9 Map of self built data sets based on graph optimization

实验采用的数据集信息如表1所示，表2清楚地展现出基于前后端图优化的方法相比与solvePnPRansac方法在运行速度几乎相等的情况下，在精度上有明显的优势，且拥有较好的实时性。

表1 实验数据集信息Table 1 Experimental data set information

表2 实验结果分析Table 2 Experimental result analysis

4 结 论

在图优化方法的基础上，提出了在视觉SLAM前后端都使用图优化方法来优化移动机器人位姿的方案。该方法利用深度相机作为传感器，通过ORB算子在较短时间内完成RGB图像的特征点提取与匹配，运用图优化的方法计算得到相机的初步位姿，采用DBoW2算法进行回环检测，基于图优化的方法进行后端优化，并利用优化求解得到的移动机器人位姿构建出移动机器人运动轨迹以及三维场景地图，通过基于floor数据集和自建数据集的两组实验验证了本算法的准确性和高效性。