基于粒子群算法的风光互补发电系统配置优化设计

， ，，， ，

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 310014；3.浙江工业大学 政治与公共管理学院，浙江 杭州 310023)

在现今的可再生能源中，风能资源和太阳能资源发展速度快、成本较低，具有大规模可开发利用价值，受到普遍重视。同时，基于风能与太阳能资源的互补性，风光互补系统得到了很大的发展。但是由于风力资源、太阳能资源在时间上和空间上的不确定性，每天的发电量受天气的影响很大，导致发电与用电负荷的不平衡[1]。因此，风光互补发电系统的组成及配置成为提高其性能的关键，诸多专家学者对此进行了深入研究。赵昕宇等[2-6]通过运用遗传算法对风光互补发电系统的最小净成本和最优化配置进行了研究；Sopian 等[7]用牛顿算法对系统进行了优化配置；Kaiser 等[8]运用TRNSYS16模拟软件对系统的运行进行仿真，同时进行了成本评估；艾斌等[9-10]提出了一种利用CAD技术对系统配置进行优设计化的方案。但多数优化方法都集中在解决单目标问题，包括在某些特定条件约束下的解。研究采用多目标规划，同时优化系统的经济性能和技术性能，并运用粒子群算法进行求解，最后通过实例对优化方案进行了评估。

1 风光互补发电性能分析

1.1 经济性能

系统的经济性是评价风光互补发电系统的重要标准[11]。计算中以系统总成本作为目标函数，即

Mmin=Mf·Nf+Mp·Np+Mb·Nb+M0

(1)

式中：Mmin为系统总成本；Mf为风力机单价；Nf为风力机数量；Mp为光伏电池单价；Np为光伏电池数量；Mb为蓄电池单价；Nb为蓄电池数量；M0为其他附件价格。

1.2 技术性能

光伏阵列发电功率与风力发电机组发电功率满足负载的功率，总发电量也必须满足负载耗电量。同时输入项中有一个不能连续发电时间，通过不能连续发电时间来控制变量，保证在最极端的情况下，蓄电池的放电量能满足系统的负载要求。宋洪磊等[12-13]研究了蓄电池的放电量和最小容量、风力发电机最小功率和太阳能电池板最小功率，其中蓄电池的放电量应满足：

1) 光伏阵列发电功率与风力发电机组发电功率满足负载功率，总发电量也必须满足负载耗电量Pa+Pp≥Pr，Qa+Qb≥Qr。

2) 通过验证计算，输入项中有一个不能连续发电时间，通过不能连续发电时间来控制变量，保证在最极端的情况下，蓄电池的放电量能满足系统的负载要求Bi≥Bmin，Pfi≥Pfmin，Pp≥Ppmin。

蓄电池最小容量Bmin满足

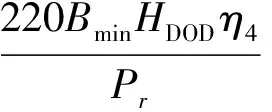
(2)

式中：Pr为用电负荷日平均用电功率；HDOD为蓄电池放电深度；η4为蓄电池误差余量，一般取0.9。

在太阳能不能进行发电时，多为阴雨天气，此时风速和持续时间均大大超过年平均风速和时间，所以可在此选择风机日工作时间为8 h/d，风力发电机最小功率Pfmin满足

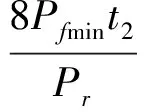
(3)

在风力机不能进行发电时，多为连续晴天，而且每天日照时数大大高于年平均日照时数，所以可在此选择太阳日照时间为8 h/d，太阳能电池板最小功率Ppmin满足

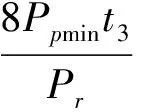
(4)

式中：t1为当地风力发电机和太阳能电池组件不能同时发电的最大连续时间；t2为太阳能电池组件不能发电的最大连续时间；t3为风力发电机不能发电的最大连续时间。

2 优化算法-粒子群算法

粒子群优化算法 (Particle swarm optimization，简称PSO)是由Kennedy等[14-17]通过将鸟类及鱼类的觅食过程中的群行为模拟成二维空间上的探索模型，于1995年开发而成的优化算法，可应用于连续型变量的非线性设计的求解问题。粒子群算法模型简洁，却具有优异的探索效率、良好的收敛性及精度，与其他优化算法相比具有令人瞩目的优异性。

整个系统的优化算法如图1所示，阴影框中所示风光互补系统计算见图2。

图1 系统优化设计算法流程图Fig.1 Flowchart of system optimization design algorithm

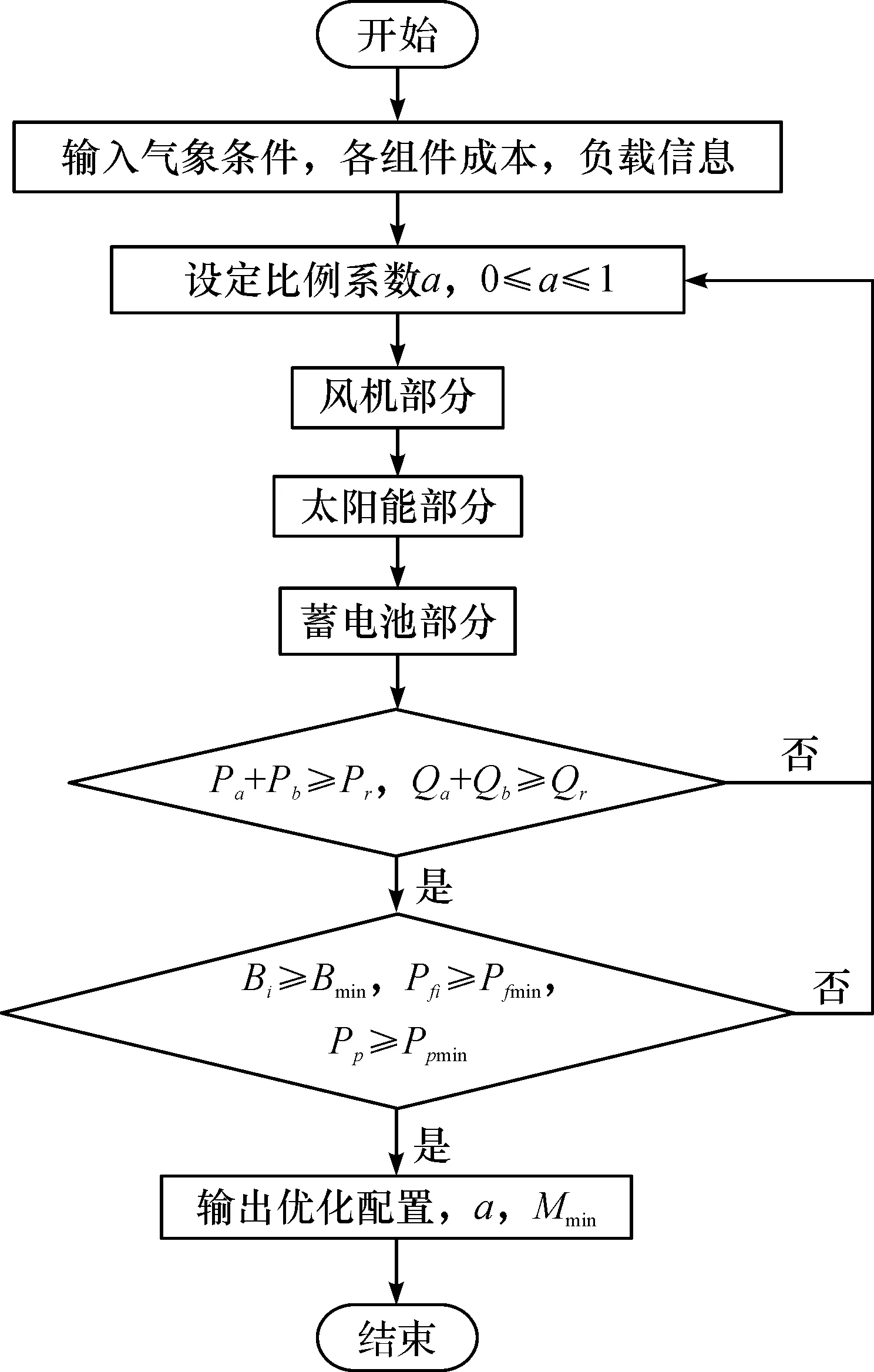
图2 风光互补系统计算流程图Fig.2 Flowchart of complementary system calculation

PSO算法的核心公式仅含有速度和位置2 个变量，结构简洁却效率优异。对于含有制约条件的约束问题的求解也可以通过引进惩罚函数的手段来进行求解。在PSO算法中，某个粒子将自身探索过程中的最优值作为Pbest进行保存，同时，对所有个体的最优值再次选择出群体最优值作为Gbest进行保存，并且对全体共享信息。群体中其他个体参考以上两种最优值来对自身的位置和速度进行调整，粒子群在这种不断更新的探索过程中所寻求而得的达到精度要求的具有最好适应度群最优值Gbest即为所求的解。

(5)

(6)

式中：i为粒子的序号；k为现在的探索回数；vk为现在第k回探索是的速度；wk为对vk产生影响的惯性参数；c1为对Pbest的移动倾向产生影响的局部解趋势参数；c2为对Gbest的移动倾向产生影响的全局解趋势参数；r1，r2为在0～1之间的随机数。

通过引进惩罚函数求解含有制约条件的约束问题，即

minf(x)

(7)

subj tohi(x),i=1,2,…,m

(8)

gi(x),i=m+1,m+2,…,m+p

(9)

式中：f(x)为目的函数；hi为等式制约条件；gi为不等式制约条件；i为制约条件序号；m+p为制约条件总数；m为等式制约条件数；p为不等式制约条件数。

采用多目标制约函数，就是能够让整个软件计算更为科学、全面，从多方面进行考虑，既满足了负载要求，考虑了最极端环境下的发电情况，同时又能从经济性出发，尽量使成本最小化，兼顾了多方面的要素。为了使求解过程更为便捷，决定引入随机数α，即风力机发电量占总发电量的比重，在计算过程中改变α来得出最终结果，在求解随机数α时，采用粒子群算法，该算法的好处就是带惩罚函数，可以有效地解决多个制约条件，达到最优化，协调风力机组和光伏阵列的发电比例。

3 实例分析

3.1 实际案例

利用上述优化方案对某工业园区20 kW的风光互补发电系统进行了优化。当地气候条件为杭州，纬度30°14′N，经度120°10′E，空气相对湿度60.6%，海拔高度41.7 m，不能连续发电时间3 d。风能、太阳能资源情况见表1。

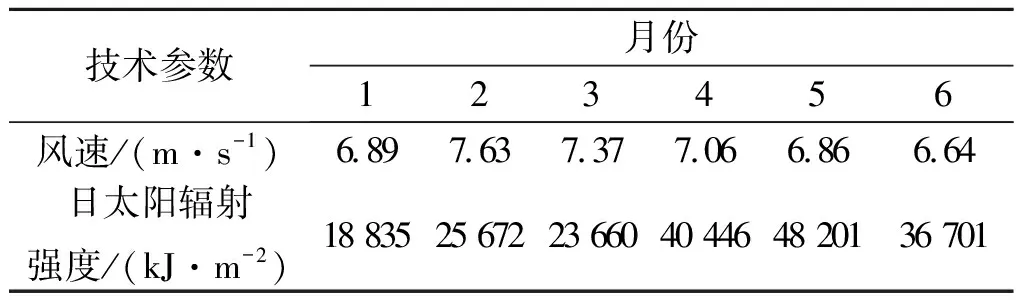
表1 地面10 m处全年平均风速及当地太阳辐射强度

技术参数月份789101112风速/(m·s-1)6.846.917.207.106.476.78日太阳辐射强度/(kJ·m-2)48 32852 92442 91831 16019 66727 167

根据相关厂家数据选择了项目中使用的风力发电机、太阳能阵列和蓄电池型号，参数为

1) 风力发电机组技术参数：型号XG-5KW，峰值功率6 000 W，额定转速220 r/min，额定功率5 000 W，输出电压192 V，风轮直径5 m，启动风速3 m/s，工作风速3～25 m/s，切出风速50 m/s，运行寿命15 年。

2) 光伏电池模块技术参数：型号TOP210，额定峰值功率210 W，额定峰值电压27.3 V，额定峰值电流7.70 A。

3) 蓄电池技术参数：型号NP2-3 000，化学类型为铅酸蓄电池，蓄电池容量3 000 A·h，工作电压2 V，回路效率86%，最大放电深度率70%。

3.2 风光互补发电系统经济性能分析

表2为单独采用风能、太阳能以及风光互补发电系统的经济性能分析。采用风光互补发电时实际风力机组的发电量为15 kW·h，光伏发电量为7.56 kW·h，以风能发电为主，总价格为61.2 万元。

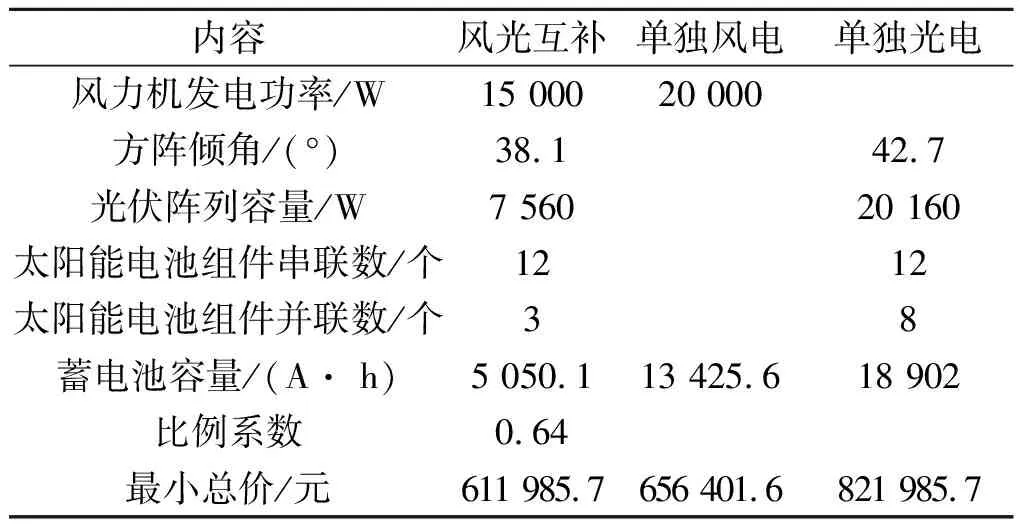
表2 风光互补发电系统优化结果汇总

当采用单一的风力系统进行发电时，总价为65.64 万元。风力发电相较于光伏发电，风力发电的成本应该是较低的。但是采用单一的风力发电系统时，系统造价却比采用风光互补发电系统时的造价还高，这是由于蓄电池成本比较高的原因。

当采用单一的光伏发电系统进行发电时，需要TOP210型号的光伏电池12 串8 并形式，实际发电量为20.16 kW·h ，总价为82.2 万元。相对来说，光伏阵列的价格是最高的，这是因为当地太阳能资源有一定季节性的分布，4～9 月份辐射强度更大，而其余几个月份就略有不足了。但是负载随季节性的波动却没有如此之大，为了满足负载的要求，储能设备也相对需要更多。所以光伏阵列发电的成本最为高昂。

3.3 风光互补发电系统技术性能分析

图3～5为风光互补发电系统的各月的风力机发电量情况。从图3中可以得出：由于该工业园区处于江边，风能资源相较于太阳能资源会更为丰富，而且一年四季相比来说，由于风力发电也更为均衡，因此风力发电占主导地位。总体上光伏发电量明显小于风力发电量，但夏季的光伏发电量要好于冬季，因为从4月起至9月，日照强烈，光伏阵列发电效果变好，发电量增加，但在6月时受梅雨季节影响又面临一个低谷。图4为单独风能发电系统的各月的风力机发电量情况。从图4中可以得出：此地区风能资源较好，受季节影响较小，风力发电量也较平均，能大致满足负载需求。图5为单独光能发电系统的各月的风力机发电量情况。从图5中可以得出：各月的光伏发电量极不平衡，尤其是在光照强度最低的月份。

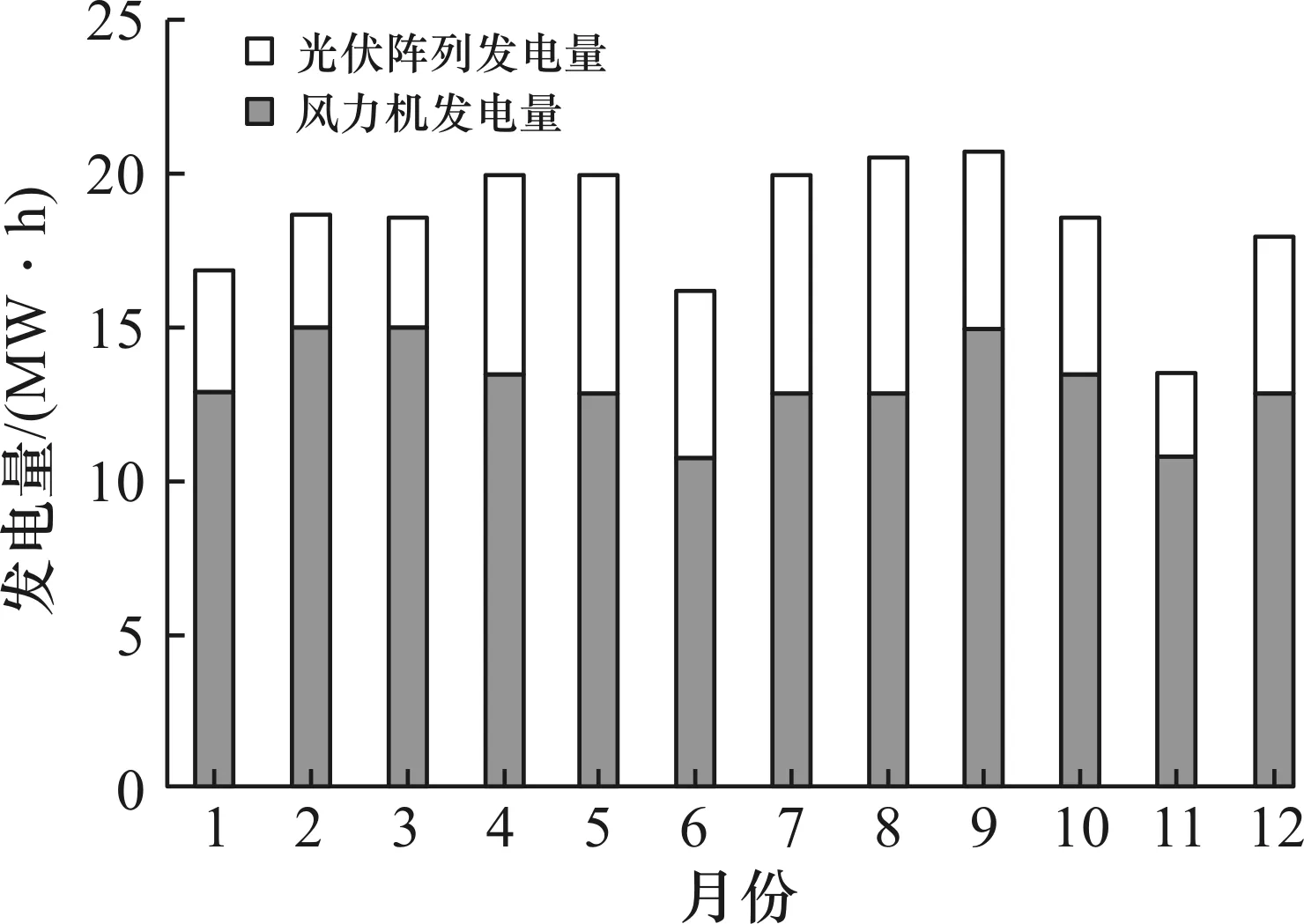
图3 各月的风力机与光伏阵列发电量图Fig.3 Monthly wind turbine and PV array power generation map

图4 各月的风力机发电量Fig.4 Monthly wind turbine power generation

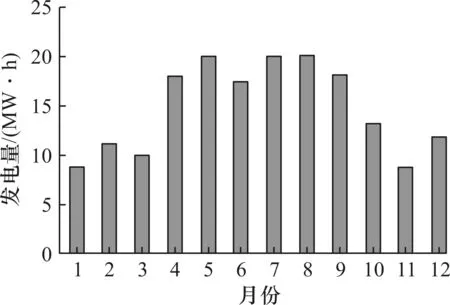
图5 各月光伏阵列发电量Fig.5 Monthly PV array power generation

图6为各月风光互补发电系统，单一的风力发电系统，单一的光伏阵列发电系统的负载满足率对比情况。从风光互补各月负载之间的关系可以得出：大多月份均能满足负载要求，尤其是在夏季的几个月，均有电量结余，而在其余几个不能满足负载要求的月份，蓄电池的充放电就能发挥很大的作用。但从单独风力机负载满足率中得出：夏季本应该是用电需求最旺盛的时候，发电量却相比其他几个月有所下降，为了保证系统供电的可靠性，整个系统在储能设备上必须加大投入。因此，单独光伏发电系统各月的负载满足率也是最差的，这样不平衡的发电量导致储能设备投入的增加，总价也最为高昂。从图6中可以得出：1月至3月，风力机的负载满足率稍高于风光互补的负载满足率，而它们远高于光伏阵列的负载满足率；在4月至6月，风光互补的负载满足率则高于风力机和光伏阵列；在6月，3个负载满足率基本达到一致；从6月至8月，由于夏季光照强度高，光伏阵列的负载满足率高于风光互补和风力机；而从9月至12月，风光互补和风力机的负载满足率基本不相上下，但两者远高于光伏阵列光伏阵列。整体来说，风光互补的负载满足率最具优势，单独风力机次之，而单独光伏阵列的负载满足率存在很大的不稳定性，效果最差。

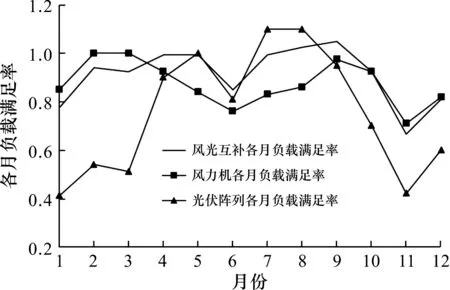
图6 各月负载满足率Fig.6 Monthly load satisfaction rate

3.4 子系统成本敏感性分析

风光互补发电系统是由两大子系统组成，一个是风力发电，另一个是光伏发电，以下研究当一个子系统改变以后对于整体系统的成本的变化。除开两大子系统，储能设备蓄电池的成本影响也较大，但是在给定气候、负载的情况下，优化设计时首先考虑的就是负载与发电量的匹配情况，所以不论蓄电池的价格如何变化，对两个子系统的影响并不是很大。在此不予研究。

3.4.1 风力机成本敏感性分析

在3.1节所示的负载与气候条件下，改变风力机价格，将其价格从1 万元设置到5 万元，统计其比例系数的变化，则风力机成本变化对整个系统的影响结果如图7所示。

从图7中可以得出：当风力机价格不断增加时，比例系数(风力发电量占总发电量的比例)随之减小。而且前期下降速度较快，到后期逐渐平稳。这是因为在前期，风力机组件价格低廉，相较于光伏发电其成本低，而且风能资源良好，不呈现季节性影响，可以尽可能采用风力进行发电，甚至为了让系统更为可靠，可以在满足负载的情况，在风力机成本如此低的情况，再多配备机器当作备用也较为可行。而后期，当风力机的价格逐渐升高，相对于光伏发电，它的价格优势下降，系统更趋于稳定，相对来说风力机的数量和风力发电量的多少对整个系统的影响就降低了，所以曲线显示得也更为平稳。

图7 系统比例系数随风力机成本变化图Fig.7 System proportional coefficient changes with wind turbine cost

3.4.2 光伏组件成本敏感性分析

同理，改变光伏组件价格，将其价格从每块600 元设置到1 000 元，统计其比例系数的变化，光伏组件成本变化对整个系统的影响结果如图8所示。

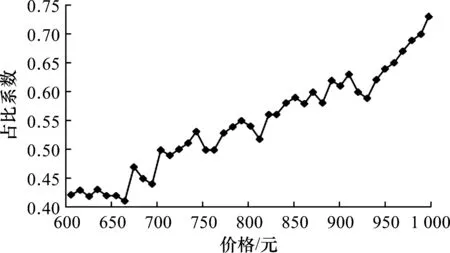
图8 系统比例系数随光伏电池成本变化图Fig.8 System proportional coefficient changes with the cost of photovoltaic cells

从图8中可以得出：当光伏电池价格不断增加时，比例系数(风力发电量占总发电量的比例)也在随之增加，而且全过程的增加趋势都较相似。这是因为相对于风力发电来说，光伏发电在下沙地区更受季节性的影响，所以在优化配置时，确实会有一定的影响，但是其影响却不如风力机价格改变对整个系统影响的变化大。

由此在此项目中，对于成本敏感性分析可得出：在整个发电系统中，风力组件的价格对整体系统的经济性影响更大。

4 结 论

针对某工业园区所在的研究区域，采用PSO粒子群优化算法对构成混合发电系统的风力发电模块、太阳光伏电池发电模块和蓄电池模块等主要模块的规格在所设定的气象和负荷条件下进行了优化设计，在达成系统成本最小的要求下可迅速寻找到满足条件的最优化方案，利用上述优化方案对工业园区20 kW的风光互补发电系统进行优化。从风光互补发电系统的经济性能分析，采用风光互补系统发电的总价格比单一的风力机发电低4.44 万元，比单一的光伏阵列低21 万元，在经济性能上优势明显；从风光互补发电系统的技术性能分析，风光互补发电系统的发电量和负载满足率更适合用户需求，在夏季用电高峰期甚至超过用户需求，多余的电量储存于蓄电池，在其余几个不能满足负载要求的月份，发挥重要的作用。因此，基于PSO粒子群优化算法优化后的风光互补发电系统在发电效率和成本价格具有最大的优势，满足工业园区在实际应用中的要求。