浅谈“数与运算”总复习中知识点的串联方法
周嘉明

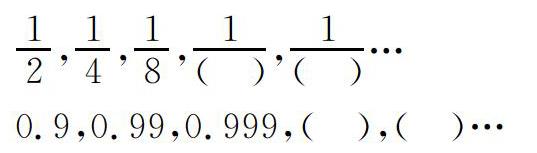
[摘 要]在教学“数与运算”总复习时,教师需要将其中的各个知识点串联起来,使学生明晰各个知识点之间的联系和区别,从而真正理解和掌握所学知识。
[关键词]数与运算;总复习;知识点;串联;方法
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2018)33-0028-01
“整理与反思”“练习与实践”是数学总复习的两个基本教学形式,通过“整理与反思”,引导学生梳理所学知识,查漏补缺;通过“练习与实践”,引导学生巩固技能,拓展思维。那么,数学教师应如何展开复习教学呢?
一、把握特点,根据认知经验分類整理
整理旧知应避免记流水账,既要将所有的知识点一一列举,又要避免随意性。因此,教师在指导学生梳理知识时要提供一些素材,这些素材要能真实再现和准确反映学生的学习经验,并以问题为导向,以完成任务为驱动,这样才能取得满意的复习效果和较高的复习效率。
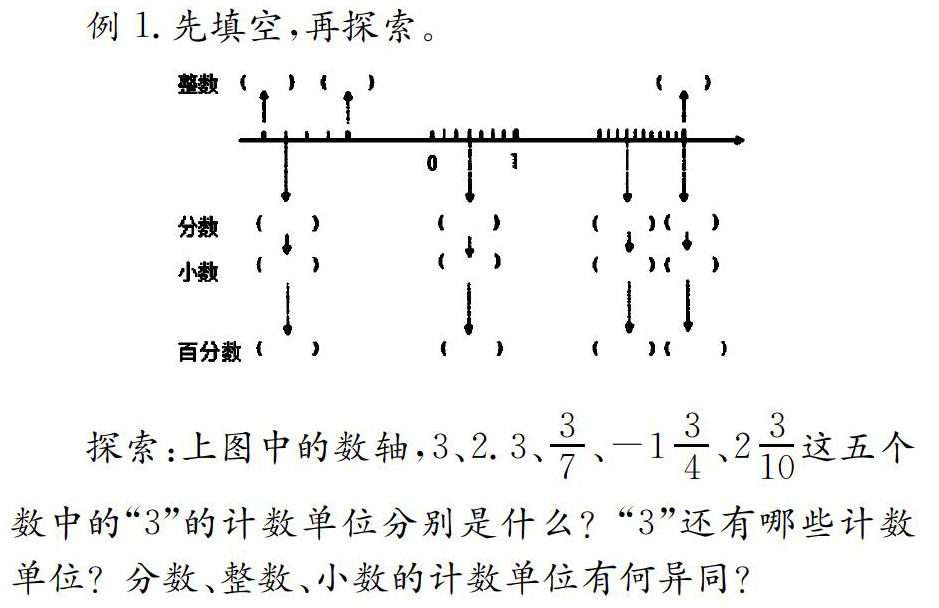
例1.先填空,再探索。
探索:上图中的数轴,3、2.3、37、-134、2310这五个数中的“3”的计数单位分别是什么?“3”还有哪些计数单位?分数、整数、小数的计数单位有何异同?
“数的认识”内容在教材中的编排较为分散,而数轴的直观形象可以把所有的数形聚合在一起,通过坐标刻画对应关系,真实反映数的本质,有利于学生将所有的数形进行对比辨析。以问题为导向,学生在解决问题时就会自觉重构数的本质,并且不断回顾与提取已有的认知经验。在这个过程中,各种数形之间的交集和互化功能,为学生综合认识数的概念提供了便利。
二、巧借数轴,将多种数形归并整合起来
课堂教学中,教师通过设计探索题,引导学生从更高层次来理解数,升级数论。通过辨析,学生明白:整数是以最小自然数“1”为基本单位,不断累加生成其他的数,直至无穷;而分数则是表示一个比例关系,主要反映部分占整体的比重,由于平均分的总份数和选取的份数不同,分数也就不同,所以分数单位不固定。但是,分数还可以表示两数相除的意思,所以分数可以化为小数,小数实际上是分数和整数的结合体,它的小数部分的坐标表示要借助分数来实现。
例2.观察,探索。
探索(1):在数轴上找出8的所有因倍数,并用△和☆两种符号加以区别。先观察,再说出因倍数的特征。
探索(2):在数轴上找出12的因倍数,并用▲和★两种符号加以区别。仔细甄选,找出8和12的所有公约数。最大公约数与其他公约数的关系是什么?公倍数有多少个?最小公倍数与其他公倍数又是什么关系?
探索(3):8和12两个数的最大公约数与最小公倍数是什么关系?
“因数与倍数”这一内容的概念较多,而且非常抽象,是数论教学中的难点。复习时,教师可利用数轴直观化地展示因数和倍数,使学生对抽象的概念形成清晰的感性认知,这种感性认知会发展成为理性知觉。同时,借助数轴揭示因倍数的概念,不仅能直观地展示因倍数与原数的关系,而且通过位置对比,使学生可以推知倍数的个数是无限的。
三、发散思维,在原有知识经验上进行拓展
课堂教学拓展和延伸的方式有很多,可以挖掘钻研知识的深度,也可以向相关知识辐射扩张,还可以在应用上下功夫,不同方式的选择需要根据复习内容的特点而定。
例3.思考,填空。
(1)你第一眼看到“110”这个数时想到了什么?“110=6”这个算式很蹊跷,你想揭开谜底吗?课后请查阅有关“二进制计数法”的文献资料。
(2)填数,并思考每组数会无限逼近哪个定值?
12,14,18,1( ),1( )…
0.9,0.99,0.999,( ),( )…
第(1)题,当“110”只表示一个数时,它具备多重属性——自然数、正数、整数、偶数、合数;从组成来看,它包含1个百和1个十,也可视为11个十或110个一;“110”还可以表示报警电话号码。如果从二进制的角度看,十进制中的数“6”转码成二进制的数就是代码“110”。设计这样的问题,既可以培养学生的发散性思维,使学生能综合运用已学过的知识和有用的经验解决问题,又引导学生认识了计数位值。第(2)题,思考“每组数会无限逼近哪个定值”其实是极限思想的雏形,这里意在引导学生体会数轴上数点的无限性。
总之,复习好“数与运算”的内容,让学生牢固掌握一些基本的数理,有利于培养学生的数学素养。
(责编 杜 华)

