倾斜椭球各向异性介质弹性波传播特征

梁 锴 曹丹平* 印兴耀 吴国忱

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580；②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071)

1 引言

地球介质广泛存在各向异性，地震各向异性主要表现在地震波传播速度是传播方向的函数、体波间的相互耦合、横波分裂等。地震各向异性为研究地球介质结构、组分提供了新的信息[1]。一般将沉积岩近似为横向各向同性(TI)介质[2]，特别地，当ε=δ(ε为度量qP波各向异性强度的参数，δ为影响TI介质对称轴方向附近的qP波速度的参数)时，称为椭球各向异性(EA)介质。EA介质是TI介质的一种特例，其独立的弹性常数只有4个。与倾斜横向各向同性(TTI)介质类似[3-11]，当EA介质的对称轴与观测坐标系有夹角时就形成倾斜椭球各向异性(TEA)介质。Byun[12]根据射线理论研究了EA介质的地震参数。Helbig[13]总结了椭球各向异性的特征和意义。Thomsen[2]给出了表征EA介质的Thomsen参数。李磊等[14]讨论了EA介质参数的约束条件。

速度和偏振方向是弹性波传播的重要特征，也是研究地震波传播规律的重要参数，在理论研究和实际应用中具有重要作用。在各向同性介质中，弹性波速度不随传播方向而变化，P波的偏振方向与传播方向平行，S波的偏振方向与传播方向垂直。在EA介质中，弹性波速度可能随传播方向而变化，并且P波的偏振方向与传播方向不平行，SV波的偏振方向与传播方向不垂直。前人广泛研究了TI介质(包括TTI介质)的速度和偏振现象[15-21]。

研究TEA介质传播特征可以采用两种方法。一种是在本构坐标系下求取EA介质的速度和偏振等特征，然后再利用坐标旋转的方法[18]，得到观测坐标系下的TEA介质的速度和偏振等特征。该方法得到的结果是相角(传播方向与对称轴夹角)的函数[18]，难以表示为关于观测坐标系中平面波传播的极化角θ和方位角φ的函数。本文采用第二种方法，即在观测坐标系直接求取TEA介质弹性波速度和偏振特征参数。首先根据本构坐标系的EA介质刚度矩阵，利用Bond变换得到观测坐标系下TEA介质的刚度矩阵；然后建立TEA介质Christoffel方程，通过求解本征值问题得到观测坐标系下TEA介质弹性波相速度和偏振解析表达式；再通过Crampin公式由相速度推导群速度的解析表达式；最后给出了相应的数值算例。该方法的速度和偏振表达式均是关于观测坐标系中平面波传播的极化角θ和方位角φ的函数，形式直观，物理意义明确。

2 TEA介质刚度矩阵

各向异性介质是由刚度矩阵C确定的，刚度矩阵C确定了应力与应变之间的关系，但由其确定弹性波波动方程系数的物理意义很不直观。为方便理论研究和实际应用，Thomsen[2]提出了一套表征TI介质弹性的Thomsen参数

(1)

(2)

由弹性力学基本理论可知，在本构坐标系下，EA介质的刚度矩阵为

(3)

观测坐标系中的TEA介质实质上可视为由本构坐标系中的EA介质旋转形成 (图1)。因此，可以利用Bond变换[22]对本构坐标系下的刚度矩阵进行坐标变换，从而得到观测坐标系下TEA介质的刚度矩阵。

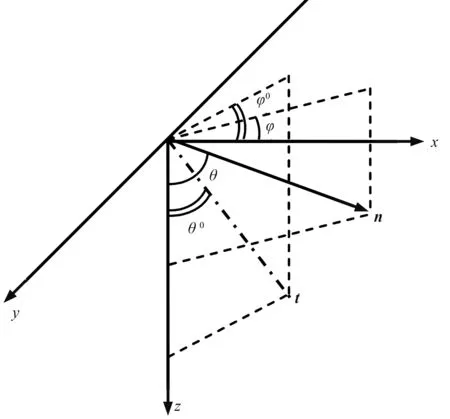
图1 TEA介质对称轴示意图θ、φ分别为传播极化角和方位角， θ0、φ0分别为对称轴倾角和方位角， n为平面波传播方向。

(4)

TEA介质刚度矩阵与三斜各向异性介质(极端各向异性介质)刚度矩阵的结构相似，即描述两种介质的弹性波方程具有同样的形式，但前者的独立弹性常数个数与EA介质一样(4个)。

3 TEA介质弹性波速度和偏振

3.1 相速度

弹性波传播速度主要包括相速度和群速度，相速度和群速度是弹性波传播的两个重要特征。TEA介质的弹性波传播特征不同于各向同性介质，其相速度和群速度不一定相等。

利用TEA介质刚度矩阵CTEA，结合弹性动力学的本构方程、牛顿运动微分方程和几何方程，得到TEA介质弹性波波动方程

(5)

式中：U=(ux,uy,uz)T为位移矢量；ρ为介质密度；t为时间；F=(Fx,Fy,Fz)T为体力项；L为空间偏导数算子矩阵，其表达式为

设式(5)的平面波解为

U=pexp[ik(n·x-Vt]

(6)

式中：x=(x,y,z)T为位置矢量；n=(sinθcosφ,sinθsinφ,cosθ)T为平面波的传播方向；V为平面波传播的速度(相速度)；k为波数；p=(px,py,pz)T为平面波的偏振方向。

将式(6)代入式(5)，并忽略体力项的影响，得到TEA介质Kelvin-Christoffel方程

(7)

式中Γ11、Γ12、Γ13、Γ22、Γ23、Γ33为VP0、VS0、ε、γ、n和t的函数。为使式(7)有非零解，必须使其系数矩阵行列式为零，求解可得TEA介质中qP波、qSV波和SH波相速度的解析表达式

(8)

其中

(9)

式(8)表明：TEA介质中qP波的相速度为VP0、ε、θ、φ、θ0、φ0的函数，与VS0和γ无关。qSV波的相速度为一常数VS0，与VP0、ε、γ、θ、φ、θ0、φ0无关，说明在TEA介质中qSV波的相速度呈各向同性。SH波的相速度表达式与qP波类似，SH波的相速度为VS0、γ、θ、φ、θ0、φ0的函数，与VP0和ε无关。综上所述：在TEA介质中qP波和SH波相速度呈各向异性，相速度空间等值面不是椭球面；SV波相速度呈各向同性，相速度空间等值面为球面。

3.2 群速度

群速度是各向异性介质弹性波的另一个重要特征，它决定波的能量传播速度与方向，在地震波旅行时正演和反演中起重要作用。在各向异性介质中，群速度不能由Christoffel方程得到，群速度不仅是相速度的函数，而且依赖于传播方向，在频散关系中以隐函数形式出现，因此计算相对较复杂。

根据Crampin[23]推导各向异性介质群速度的思想，可得到一般各向异性介质群速度的三个分量表达式

(10)

其中V为平面波传播速度(相速度)。根据TEA介质的相速度表示式(式(8))，可得TEA介质qP波、qSV波和SH波的群速度表示式。

qP波群速度的三个分量为

(11)

其中

G=sinθsinθ0cos(φ-φ0)+cosθcosθ0

qP波群速度的值为

(12)

对比式(8)与式(12)可知，在TEA介质中除某些特定方向外，qP波的相速度与群速度不相等。另外，在TEA介质中qP波的群速度与VS0和γ无关。

经过推导可知，qP波群速度的三个分量满足

(13)

式(13)表示三维空间的一个对称轴倾斜的椭球面，说明在TEA介质中qP波群速度等值面为对称轴倾斜的椭球面，其扁率为

(14)

由式(14)可见：αP只与ε有关，ε越大，αP越大；ε越小，αP越小，群速度等值面越接近于球面； 当ε=0时，αP=0，群速度等值面由椭球面变为球面，即TEA介质退化为各向同性介质。

qSV波群速度与相速度大小相等、方向相同，即

(15)

qSV波群速度的值为

(16)

同理可以证明

(17)

式(17)表示三维空间中的一个球面，说明在TEA介质中qSV波的相速度和群速度等值面均为球面，呈各向同性特征。

SH波群速度的三个分量为

(18)

SH波群速度的值为

(19)

对比式(8)与式(19)可知，在TEA介质中除某些特定方向外，SH波的相速度与群速度不相等。另外，在TEA介质中SH波的群速度与VP0和ε无关。

同理可以证明

(20)

式(20)表示三维空间的一个对称轴倾斜的椭球面，说明在TEA介质中SH波群速度与qP波类似，群速度等值面为对称轴倾斜的椭球面，其扁率为

(21)

由式(21)可见：αSH只与γ有关，γ越大，αSH越大；γ越小，αSH越小，群速度等值面越接近于球面；当γ=0时，αSH=0，群速度等值面由椭球面变为球面，即TEA介质退化为各向同性介质。

3.3 偏振

将弹性波的相速度分别代入TEA介质Chris-toffel方程并求解，其归一化的通解为相应波型的偏振方向(图2)。

(22)

其中

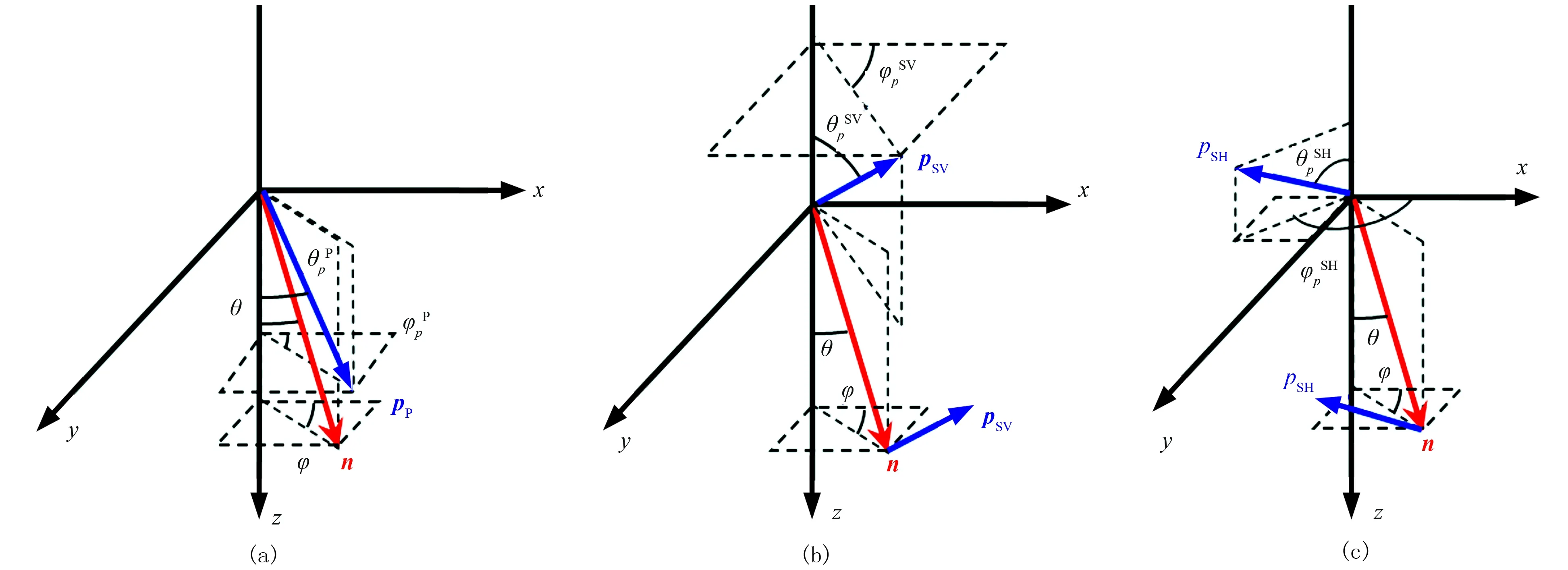
图2 qP波(a)、qSV波(b)、SH波(c)偏振示意图

(23)

因为pP×n≠0，说明在TEA介质中P波偏振方向pP与传播方向n不平行，而是存在一定角度，因此在TEA介质中将P波称为准P波或qP波。

(24a)

(24b)

其中

(25)

因为pSV·n≠0，说明在TEA介质中SV波偏振方向pSV与传播方向n不垂直，而是存在一定角度，因此在TEA介质中将SV波称为准SV波或qSV波。

(26a)

(26b)

(27)

因为pSH·n=0，说明在TEA介质中SH波偏振方向pSH与传播方向n垂直，为纯S波。

假设传播方向n=(sinθcosφ,sinθsinφ,cosθ)T和对称轴方向t=(sinθ0cosφ0,sinθ0sinφ0,cosθ0)T都经过坐标轴原点，则有如下推论：

(1)经计算pP·pSH=0，pSV·pSH=0，pP·pSV=0，说明TEA介质中qP波、qSV波和SH波的偏振方向两两垂直，符合各向异性介质弹性波的偏振规律。

(2)经计算pSH·t=0，说明在TEA介质中SH波偏振方向pSH与t垂直，又由于pSH与n垂直，因此pSH垂直于t和n确定的平面。此外，由于qP波、qSV波和SH波的偏振方向pP、pSV、pSH两两垂直，则pP、pSV平行于t和n确定的平面。

(3)在TEA介质中pP、pSV是n、t、VP0、VS0和ε的函数，pSH仅是n、t的函数，而与TEA介质的VP0、VS0、ε和γ均无关。

(4)在TEA介质中，qSV波相速度和群速度呈各向同性特征，但其偏振方向呈各向异性特征。

4 数值算例

为了验证前文对TEA介质弹性波速度和偏振现象的认识，设计了一组均匀TEA介质模型(表1)。模型1与模型2的对称轴倾斜方向相同，各向异性参数不同；模型2与模型3的对称轴倾斜方向不同，各向异性参数相同。

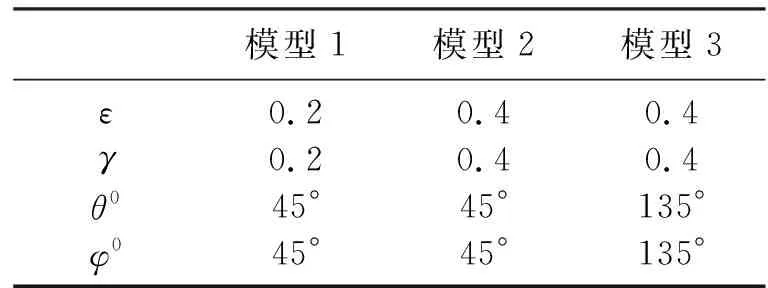
表1 模型介质参数

注：VP0=3000m/s，VS0=1500m/s，ρ=2000kg/m3

图3～图5分别为计算的模型1～模型3的弹性波速度。由图可见：qP波和SH波相速度呈各向异性特征，相速度空间等值面不是椭球面(图3a、图3c、图4a、图4c、图5a、图5c)，qP波和SH波群速度等值面为椭球面，且随着ε和γ的增大，椭球的扁率也增大，说明各向异性程度随ε和γ的增大而增大(图3d、图3f、图4d、图4f、图5d、图5f)；qSV波的相速度和群速度大小相等，方向相同，速度等值面均为球面，表明qSV波的相速度和群速度是各向同性的，与各向异性参数和对称轴倾斜方向无关(图3b、图3e、图4b、图4e、图5b、图5e)； 当各向异性参数保持不变，TEA介质对称轴倾斜方向发生变化时，TEA介质弹性波相速度和群速度空间等值面的形状也保持不变，只是发生了旋转，旋转的角度由对称轴倾斜方向决定(图4、图5)。

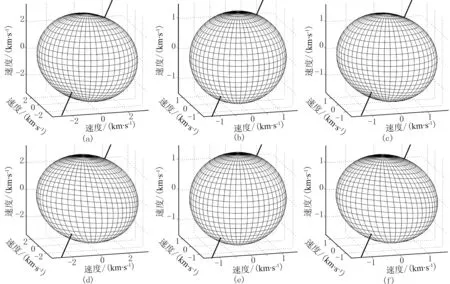
图3 计算的模型1的弹性波速度(a)qP波相速度； (b)qSV波相速度； (c)SH波相速度； (d)qP波群速度； (e)qSV波群速度； (f)SH波群速度

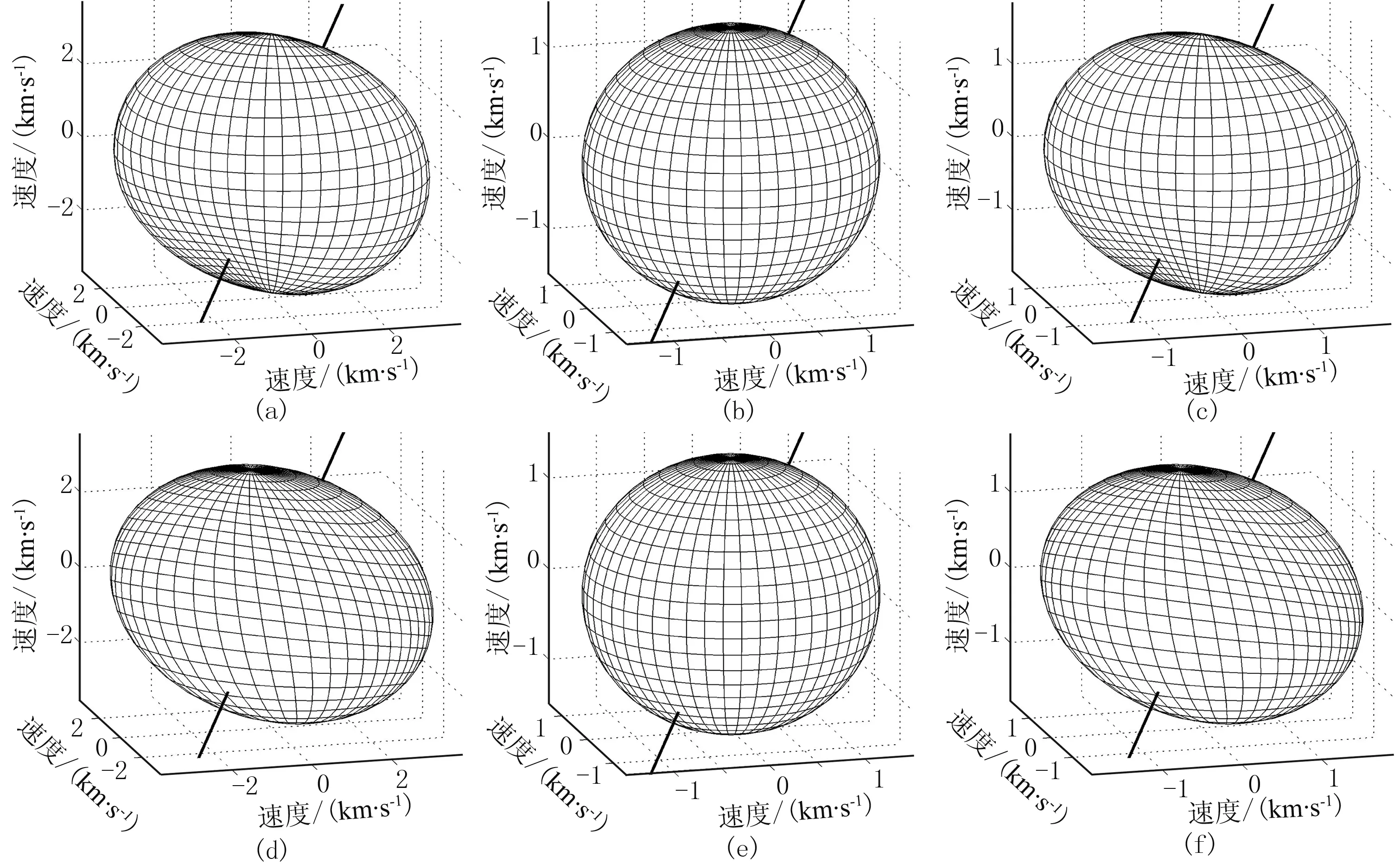
图4 计算的模型2的弹性波速度(a)qP波相速度； (b)qSV波相速度； (c)SH波相速度； (d)qP波群速度； (e)qSV波群速度； (f)SH波群速度

图5 计算的模型3的弹性波速度(a)qP波相速度； (b)qSV波相速度； (c)SH波相速度； (d)qP波群速度； (e)qSV波群速度； (f)SH波群速度

图6～图8分别为计算的模型1～模型3的弹性波偏振方向及角度。由图可见：qP波、qSV波和SH波的偏振方向相互垂直；随着各向异性参数的增大，qP波和qSV波偏振的各向异性程度也增大， SH波的偏振方向不随各向异性参数变化而变化，qP波、qSV波和SH波的偏振方向与对称轴的倾斜方向有关。

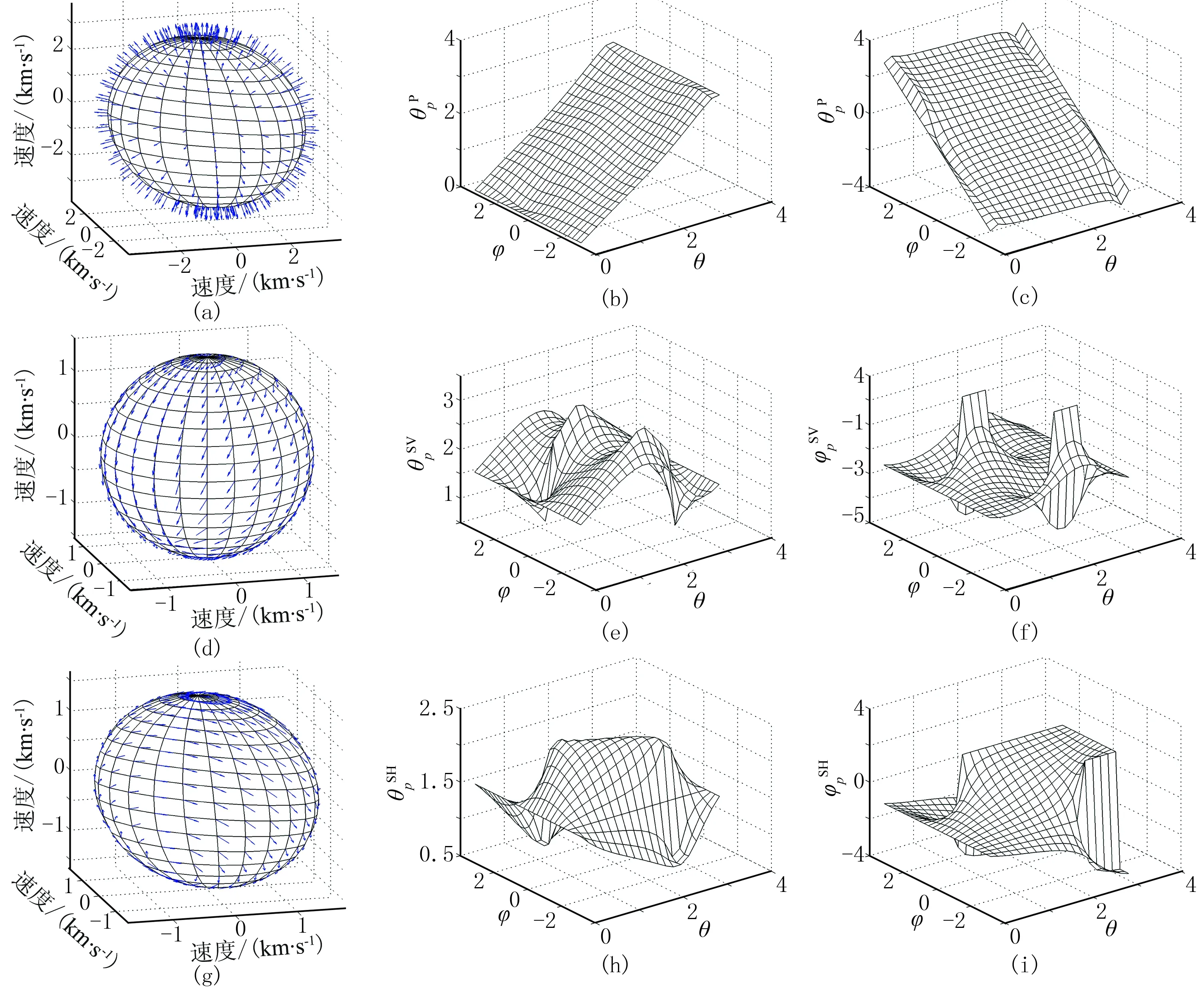
图6 计算的模型1的弹性波偏振方向及角度(a)qP波偏振方向；波偏振方向；波偏振方向；

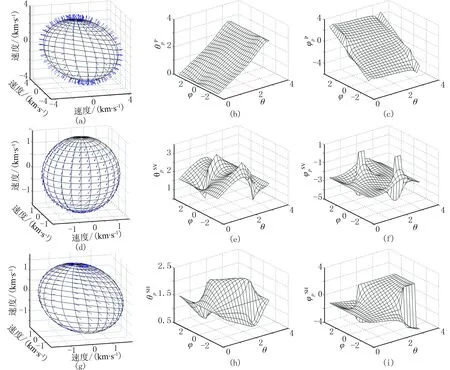
图7 计算的模型2的弹性波偏振方向及角度(a)qP波偏振方向；波偏振方向；波偏振方向；

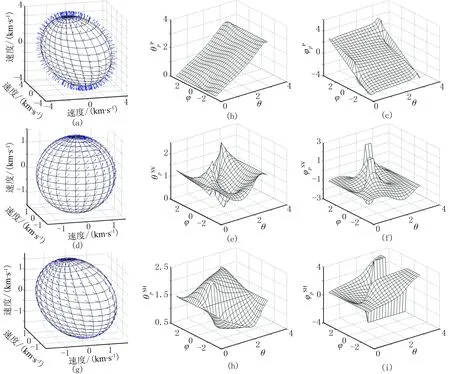
图8 计算的模型3的弹性波偏振方向及角度(a)qP波偏振方向；波偏振方向；波偏振方向；

5 结束语

本文在观测坐标系下直接求取了TEA介质弹性波速度和偏振方向，理论分析和数值算例结果表明：

(1)TEA介质qP波和SH波相速度呈各向异性特征，相速度空间等值面不是椭球面；两者的群速度等值面为对称轴倾斜的椭球面，其扁率随各向异性参数增大而增大。

(2)TEA介质qSV波相速度与群速度大小相等、方向相同，速度空间等值面均为球面，即TEA介质qSV波相速度和群速度呈各向同性特征。

(3)TEA介质qP波和qSV波的偏振方向由传播方向、对称轴倾斜方向、VP0、VS0和各向异性参数ε共同确定，而与各向异性参数γ无关。

(4)TEA介质SH波偏振方向只由传播方向和对称轴倾斜方向确定，而与TEA介质的VP0、VS0、各向异性参数ε和γ均无关，并且SH波偏振方向垂直于传播方向和对称轴方向所确定的平面。