VTI介质起伏界面混合网格旅行时线性插值计算方法

王 琦 李庆春 王芷琪

(①长安大学地质工程与测绘学院，陕西西安 710054; ②中国航空油料有限责任公司西北公司，陕西西安 710082)

1 引言

沉积盆地中页岩的各向异性与具有垂直对称轴的横向各向同性介质(VTI介质)相似[1]，而在复杂的构造环境中，如山麓或推覆构造区域，还需要考虑具有倾斜对称轴的VTI介质(TTI介质)[2]。在中国存在着大量的复杂构造发育地区，由于近地表地形的强烈起伏，加之地下构造复杂，使得计算静校正量、客观识别地震波以及实现地下目标的精确地震成像，都成为具有挑战性的难题。

VTI介质是一种最为常见的各向异性介质。Thomsen[3]根据弹性系数给出了一套各向异性参数，并分析了具有弱各向异性的VTI介质中地震波的传播特征，通过对相速度计算公式的近似处理，导出了目前仍在广泛使用的正常时差公式；在Thomsen研究工作的基础上，Sena[4]在弱各向异性线性近似下，分别推导了qP波、qSV波和qSH波群速度随群角变化的表达式。

在VTI介质波场正演模拟中，射线追踪方法具有显示直观、计算效率高以及对模型有较高适应能力的优点。目前众多学者已经将各向同性介质中的射线追踪算法陆续推广到了各向异性介质中。如Faria等[5]将旅行时非线性插值算法推广到各向异性介质中，计算了初至qP波旅行时，但在计算每个节点旅行时的时候，在每个网格中都要分别计算射线方向与介质对称轴的夹角，因此当模型区域较大时，计算效率往往比较低；邓怀群等[6]对旅行时非线性插值算法进行了改进，可用于计算VTI介质中直达波、反射波和透射波的旅行时，但在模型剖分过程中网格仍为单一的矩形网格，在计算过程中如果网格过大则降低了计算精度，若网格太小则降低了计算效率；Alkhalifah[7]利用有限差分求解程函方程实现了各向异性介质中初至波旅行时的计算，但是难以实现，因此，在一般情况下，VTI介质的地震波旅行时的计算依靠在弱各向异性假设条件下的扰动理论对各向同性参考模型的旅行时校正的方法来实现；Zhou等[8]介绍了群速度在任意各向异性介质中的计算方法，并与最短路径射线追踪方法结合，实现了二维和三维任意各向异性介质中初至波和一次反射或反射转换波的射线追踪，该方法计算原理简单，易于实现，而且可以适应较复杂的模型，但在实现过程中，为了提高计算精度，在矩形网格边界上或长方体各个面上增加了次生节点，牺牲了计算效率；赵爱华等[9]对旅行时最小树算法和地震波群速度的射线角近似表示进行了改进，计算了初至qP波、qSV波和qSH波的旅行时，理论上具有较高的计算效率和精度，但在较复杂的地质模型中，往往由于网格剖分的原因导致计算精度或效率达不到预期效果；马德堂等[10]利用Thomsen给出的VTI介质中相速度、群角、相角以及群速度之间的精确函数关系结合旅行时非线性插值法，实现了VTI介质初至qP波的旅行时计算，由于在各向异性介质中地震波群速度和群角被表示成了相角的复杂关系，为了精确计算给定群角的群速度，要进行反复搜索计算，因此计算量较大、效率较低；李建国等[11]利用传统的试射法实现了VTI介质中反射qP波旅行时的计算，试射法在计算过程中利用了渐近线的原理，通过一次次的调整射线参数得到最终的计算结果，但在计算复杂介质时存在阴影区；马德堂等[12]利用由群角反插值相角来实线局部旅行时(网格中某个节点或插值点的旅行时)的计算，并结合旅行时非线性插值法实现了TTI介质中初至qP波的计算，虽然有原理简单、易于实现的优点，但同样存在计算效率与计算精度相互制约的缺点；白海军等[13]将波前构建法与用相速度和群速度重构的射线追踪算法相结合实现了TTI介质的初至波射线追踪，但算法实现较为复杂，且没有考虑网格剖分带来的误差，因此仍有一些改进空间；李晓玲等[14]利用在混合网格边界加入次级节点的方法求取qP波、qSV波和qSH波的群速度，结合最短路径算法实现了起伏层状VTI介质的多次波射线追踪，但在求取群速度时，如果次级节点较多，计算效率会有所下降。此外，还有学者对基于网格单元扩展的射线追踪算法做出了有益的研究[15-21]。

上述大多数算法仅针对水平地表条件下各向异性介质中的初至波、一次反射波或反射转换波的旅行时进行了计算，但对于复杂地质模型会导致阴影区域且计算效率低。而对于起伏地表条件下基于网格单元扩展的射线追踪算法，多数仍以单一的网格形状进行模型剖分，若网格间距过大则计算精度降低，若网格间距过小则计算效率降低，混合网格是有效解决这一问题的途径，如李晓玲等[14]提出的分区多步不规则网格最短路径(ISPM)算法，计算了各向异性介质混合网格起伏地表条件下的多次波的旅行时。

LTI算法是Asakawa等[22]提出的基于线性假设的网格单元扩展射线追踪算法。由于该方法计算速度快、精度高、原理简单，是传统的有限差分解程函方程方法的一种高级形式，且计算精度高于传统的有限差分解程函方程法。LTI方法近年来得到了很大发展，不少学者对该方法进行了大量研究和改进。Li等[23]对LTI算法的计算公式进行了改进，使该方法对平面波假设的依赖性降低，提高了计算精度；赵改善等[24]结合界面二次源法将该方法推广，可以用于追踪反射波旅行时，弥补了仅能计算初至波旅行时的缺陷；Cardaerlli等[25]将该方法用于椭圆各向异性介质中地震波旅行时的计算；聂建新等[26]将旅行时二次插值与线性插值方法联合，降低了累积误差；Kumar等[27]将该算法进一步推广到TTI介质中；张赛民等[28]用抛物线插值取代线性插值，减小了因线性插值引起的误差；张东等[29，30]为了求得网格加点的最小旅行时，在向前处理过程中采用了多方向循环的计算方法，弥补了计算过程中射线方向没有考虑完全导致计算节点旅行时并不一定是最小值的缺陷，并将该方法扩展到三维介质。

综上所述，近年来各向异性介质起伏界面或地表地震波传播问题倍受关注，是现阶段复杂环境地震勘探必须面对的重要问题。研究混合网格剖分，是提高基于网格单元扩展的射线追踪算法在起伏界面或地表条件下各向异性介质各种地震波旅行时计算精度和效率的有效途径。本文利用基于网格单元扩展的LTI射线追踪算法和Sena[4]推导的适用于弱各向异性介质的群速度计算公式，在向前和向后处理过程中结合分区多步计算技术，实现了一种可以计算起伏地表(界面)地震初至波以及多种类型后续波的VTI介质射线追踪算法。在利用LTI算法计算时，充分考虑了射线的传播方向，并在计算过程中采用全方位循环的方法计算各个网格节点的旅行时，以保证每一个节点的旅行时都是最小值。

2 VTI介质起伏地表混合网格LTI射线追踪方法

VTI介质混合网格LTI射线追踪方法的实现过程可以分为四个步骤：模型剖分、计算局部旅行时、计算全局旅行时和射线路径、计算后续波旅行时。

2.1 模型剖分

为了更好地逼近实际地表或速度界面，同时又能兼顾计算效率，本文采用矩形网格与不规则四边形网格相结合的方法对模型进行剖分，如图1所示。首先对整个模型区域用矩形网格剖分，分别计算地表和速度界面与网格纵边的交点，得到离散地表点和速度界面点；然后将相邻的界面离散点或网格节点依次连接，就构成一条由多条折线段组成的近似于实际地表或速度界面的折线，把这些折线段与原矩形网格边界和节点组合，构成了不规则四边形网格；最后对除地表以上的各个网格节点赋予相应速度值，就完成了对整个模型的剖分。

图1 混合网格模型剖分示意图

上述混合网格在对模型剖分时会遇到三种情况，如图1中的①、②、③所示的阴影部分。为了便于观察，将阴影部分按顺序放大，如图2所示。

(1)当地表或速度界面3个相邻的离散点都在原矩形网格的同一层内，直接连接三个相邻的离散点即可构成不规则四边形网格(图2中①)。

(2)当左端或右端的离散点和另两个点不在原矩形网格的同一层内，首先连接在原矩形网格同一层的两个离散点，然后连接与中间离散点相邻的可与另一个离散点(或原矩形网格节点)构成四边形的网格节点；依次在其他层中构造四边形网格，这样就构成了不规则四边形网格(图2中②)。

(3)当3个相邻离散点中两端的离散点和中间的离散点不在原矩形网格的同一层内，分别连接与中间离散点相邻的同一层网格内可与其余两个离散点(或原矩形网格节点)构成四边形的网格节点，依次在其他层中构造四边形网格单元，这样就构成了不规则四边形网格(图2中③)。

图2中各个颜色不同的区域组成了利用上述方法建立的混合网格。最后将Thomsen参数δ、ε和γ以及纵横波的背景速度和密度赋予各个网格节点上，这样就完成了VTI介质混合网格模型的建立。

由图1和图2可以看出，混合网格剖分逼近的地表或界面(红色实线)比单一矩形网格剖分逼近(蓝色实线)的拟合程度更高，剖分方法也更合理。

图2 混合网格剖分局部放大显示

2.2 局部旅行时计算公式

地震波运动学和动力学特征在各向异性介质中有着较大的变化，其中速度的变化最为突出。群速度和相速度不再相同，群角和相角发生了分离，如图3 所示。其中，相速度指波前的传播速度，传播方向为相位变化最快的方向，且始终垂直于波前面。而相速度矢量与介质对称轴的夹角称为相角，用θ表示，VTI介质的对称轴与z轴平行。群速度指地震波能量的传播方向，与介质对称轴的夹角称为群角，用φ表示。在各向异性介质中准确求解群速度与相速度非常困难，经过众多学者的深入研究，得到了可用于数值计算的群速度的近似计算公式[3，4，31-33]。Sena[4]在弱各向异性线性近似下，分别推导出了qP波、qSV波和qSH波的群速度vP(φ)、vSV(φ)和vSH(φ)随群角φ变化的表达式

图3 VTI介质混合网格中由规则边界计算局部旅行时示意图(a)射线从网格横边穿过； (b)射线从网格纵边穿过

(1)

式中：δ、ε和γ为Thomsen参数；vP0、vS0分别为各向异性介质对称轴方向上的相速度；ρ为介质的密度。

本文提出的混合网格由矩形和不规则四边形组成，因此在计算局部旅行时要对网格边界(主要针对旅行时已知的边界)加以区分。如果网格的AB边界与原矩形网格边界重合，如图3所示，则称此边界为规则边界； 反之，如图4所示，则称此边界为不规则边界。混合网格LTI算法仍然满足矩形网格LTI算法的前提假设。

如果AB边为规则的水平边界，如图3a所示，射线穿过AB边界的D点到达C点，则C点的旅行时tC可表示为

(2)

式中：s代表C点附近的平均慢度，在VTI介质中不再是一个常数而是群角φ的函数； Δt=tB-tA为B点与A点地旅行时差；l、d1、d2、d3的含义如图3所示。由几何关系可将式(1)表示成关于l的函数

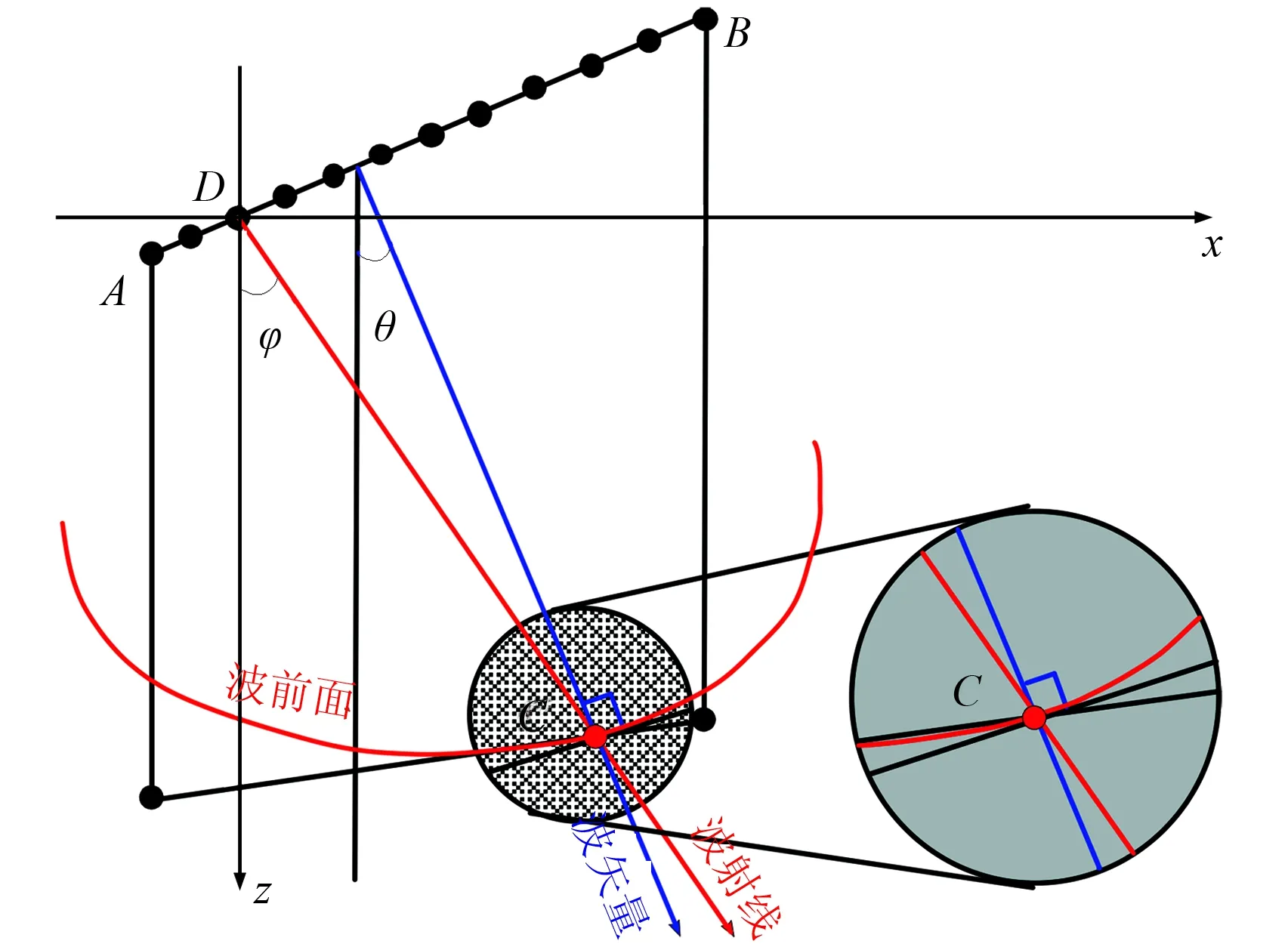
图4 由不规则边界计算局部旅行时示意图

(3)

式中：sP0和sS0分别为P波和S波的垂直相慢度；l∈(0，d2)。将式(3)代入式(2)，可得

(4)

式中tPC、tSVC和tSHC分别为穿过D点的射线以sP、sSV和sSH为慢度到达C点的局部旅行时。

根据费马原理，tPC、tSVC和tSHC在D点应满足∂tPC/∂l=0、∂tSVC/∂l=0和∂tSHC/∂l=0，可得

(5)

为了求解式(5)，构造三个关于l的非线性函数fHP(l)、fHSV(l)和fHSH(l)

(6)

式中Δt与l同号，且l∈(0，d2)，利用二分法求出以上三个函数等于零时的正实数根，即可求得局部旅行时tPC、tSVC和tSHC。解得l后即可求出D的坐标

(7)

同理,当AB边为规则的垂直边界时(图3b)，通过与上述过程类似的推导过程，构造三个关于l的非线性函数fVP(l)、fVSV(l)和fVSH(l)

(8)

同样可用二分法求出以上三个函数等于零时的正实数根，即可求得局部旅行时tPC、tSVC和tSHC。D点的坐标可表示为

(9)

当AB边为不规则边界时(图4)，将AB边界离散成若干个离散点，将每一个离散点都考虑为D点，且D点的局部旅行时通过A、B点的旅行时线性插值得到，则C点附近的慢度sP、sSV和sSH可表示为

(10)

C点的局部旅行时tPC、tSVC和tSHC为

(11a)

(11b)

以式为在混合网格VTI介质中计算局部旅行时tPC、tSVC和tSHC和插值点坐标(xD，zD)的计算公式。

2.3 全局旅行时和射线路径的计算

LTI算法的实现分为向前和向后处理两个步骤，向前处理过程得到全局旅行时，向后处理过程得到射线路径。

向前处理过程包括以下步骤。

步骤1：计算炮点所在网格的各个节点的旅行时(图5a)。

步骤2：计算炮点网格所在列的每个网格上的各个节点的局部旅行时(图5b)。

步骤3：从左向右逐步计算炮点网格右侧的每一列上所有网格节点的旅行时，具体如下：

(1)从上向下由该列左边界上的旅行时已知的节点计算右边界上的旅行时未知节点的旅行时，此时假设到达该列右边界节点的射线仅来自左边界(图5c)，黑色虚线表示射线；

(2)从下向上由网格下边界上的节点旅行时计算上边界上的节点旅行时，若计算得到的旅行时小于之前计算所得的旅行时，则更新该节点的旅行时，使其取得最小值(图5d)；

(3)从上向下由网格上边界上的节点旅行时计算网格下边界上的节点旅行时，若计算得到的旅行时小于之前计算所得，则更新该节点的旅行时，使其取得最小值(图5e)；

(4)循环执行(1)、(2)和(3)，直到整个模型最右边一列，就可以得到炮点网格所在列右侧每个节点的旅行时。

步骤4：炮点所在列左侧网格节点的旅行时的计算方法与步骤3类似，计算完成后就得到了整个模型区域中每个网格节点的旅行时(图5f)。

虽然通过上述步骤计算得到了整个模型所有网格节点的旅行时，但是该计算过程没有考虑到在复杂介质中会遇到射线逆向传播的现象，仍需按行扫描重新计算每个节点的旅行时。

步骤5：计算炮点网格所在行的每个网格上的各个节点的局部旅行时(图6a)，计算结果与按列扫描的计算结果相比较，取最小值。

步骤6：炮点网格所在行的所有网格节点的旅行时已经得到更新，从上向下逐步计算炮点网格下侧每一行上所有网格节点的最小旅行时，具体如下：

(1)从右向左由该行上边界上的节点的旅行时计算下边界上的节点的旅行时，此时假设到达该行下边界节点的射线仅来自上边界(图6b)；

(2)从左向右由网格左边界上的节点旅行时计算右边界上的节点旅行时，若计算得到的旅行时小于之前的旅行时，则更新该节点的旅行时，使其取得最小值(图6c)；

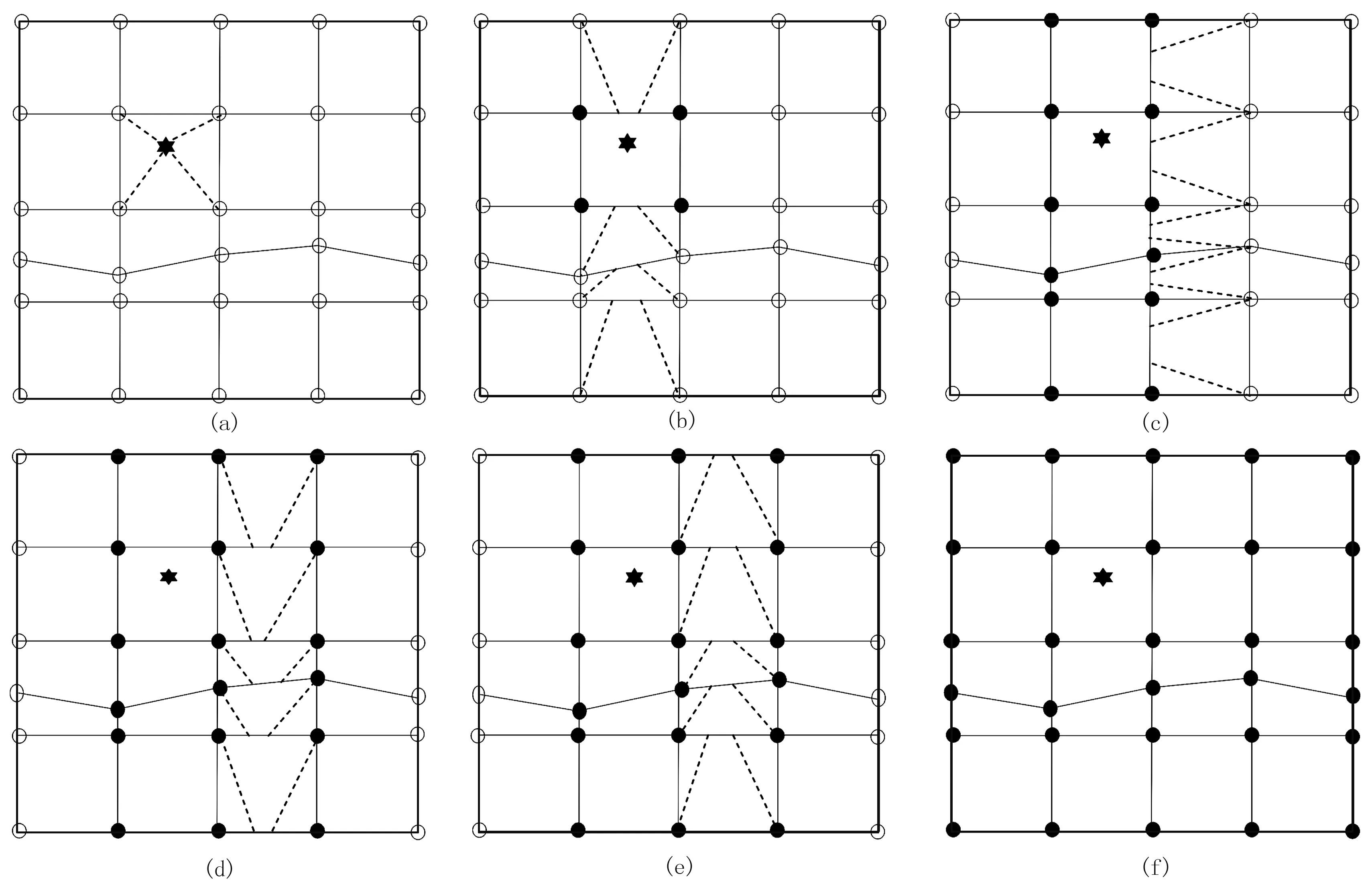
图5 向前处理中旅行时按列扫描计算网格节点旅行时(a)计算炮点网格节点旅行时； (b)计算炮点网格所在列节点的旅行时； (c)仅考虑射线来自网格左边界点的情况；d)仅考虑射线来自网格下边界的情况； (e)仅考虑射线来自网格上边界的情况； (f)网格所有节点计算完成

图6 向前处理过程按行扫描计算网格节点最小旅行时(a)计算炮点网格所在行节点的最小旅行时；(b)仅考虑射线来自网格上边界；(c)仅考虑射线来自网格左边界；(d)仅考虑射线来自网格右边界

(3)从右向左由网格右边界上的节点旅行时计算网格左边界上的节点旅行时，若计算得到的旅行时小于之前的旅行时，则更新该节点的旅行时，使其取得最小值(图6d)；

(4)循环执行(1)、(2)和(3),直到整个模型最下边一行，得到炮点网格所在行下侧每个节点的旅行时。

步骤7：计算炮点所在行上侧网格节点的旅行时，计算方法与步骤6类似，计算完成后得到了整个模型区域中每个网格节点的最小旅行时。

向后处理过程包括以下步骤。

步骤1：跟向前处理过程类似，这里将接收点作为2.2节中的C点，将接收点附近的每一条网格边界作为2.2节中的AB边，即可计算出每一条网格边界上的插值点，即D点。利用t=tmin+ds计算出接收点到其附近所有网格边界插值点的旅行时(图7a)，其中tmin为插值点的旅行时，d为接收点到插值点的距离，s为插值点的慢度；

步骤2：根据步骤1得到了接收点附近所有网格边界上的插值点坐标，那么到达接收点的射线一定经过了这些插值点，在这些点中满足t=tmin+ds取最小值的点就是要求的插值点；

步骤3：将步骤2得到的插值点坐标作为新的接收点，重复步骤1、步骤2直到插值点出现在震源所在网格的边界或节点上为止(图7b和图7c)；

步骤4：依次将震源与插值点相连得到整条初至波射线路径(图7d)，将每两个插值点(包括接收点)间的旅行时相加得到初至波的旅行时。

图7 向后处理过程计算初至波射线路径(a)计算接收点到其所在网格节点的最小旅行时，求得射线与网格的交点； (b)和(c)将确定的交点作为新的接收点，求下一个交点直到震源所在网格； (d)连接震源与计算得到的各个交点，得到射线路径

2.4 后续波的旅行时计算

将VTI介质起伏地表初至波混合网格LTI算法与分区多步计算技术[12]结合，可以实现任意多次反射(或反射转换)或透射(或透射转换)波的追踪。在计算时需要引入分区多步的思想(模型分区和多步计算)，即将整个模型区域按所需追踪的波的类型和速度特征分成相应几个独立的计算区域，在每个区域内独立进行计算。分区多步计算首先要建立模型并网格化，速度界面也要离散成不连续的点。

2.4.1 模型分区

图8所示为多次反射、透射转换波在二维层状介质模型中的分区情况，图中显示了一条在界面折返三次、转换三次的多次反射转换波。根据分区多步的思想，该多次反射转换波旅行时的计算过程可以在四个独立的计算区域(每个标号代表一个分区)内进行。具体实现过程为：该多次反射转换波由四段组成，第一段是来自地表到第二个反射界面的下行qP波，将第一、第二层作为第一个分区计算第一段下行qP波的波前，采用第一、二层的qP波速度；第二段是自第二个反射界面上的反射点到第一个反射界面的上行qSV波，将第二层作为第二个分区来计算第二段上行qSV波的波前，采用第二层的qSV波速度；第三段是自第一个反射界面反射点到第二个反射界面的下行qP波，将第二层作为第三个分区计算第三段下行qP波的波前，采用第二层的qP波速度；第四段是自第二个反射界面反射点到地表的上行qSH波，将第一、第二层作为第四个分区计算第四段上行qSH波的波前，采用第一、二层的qSH波速度。

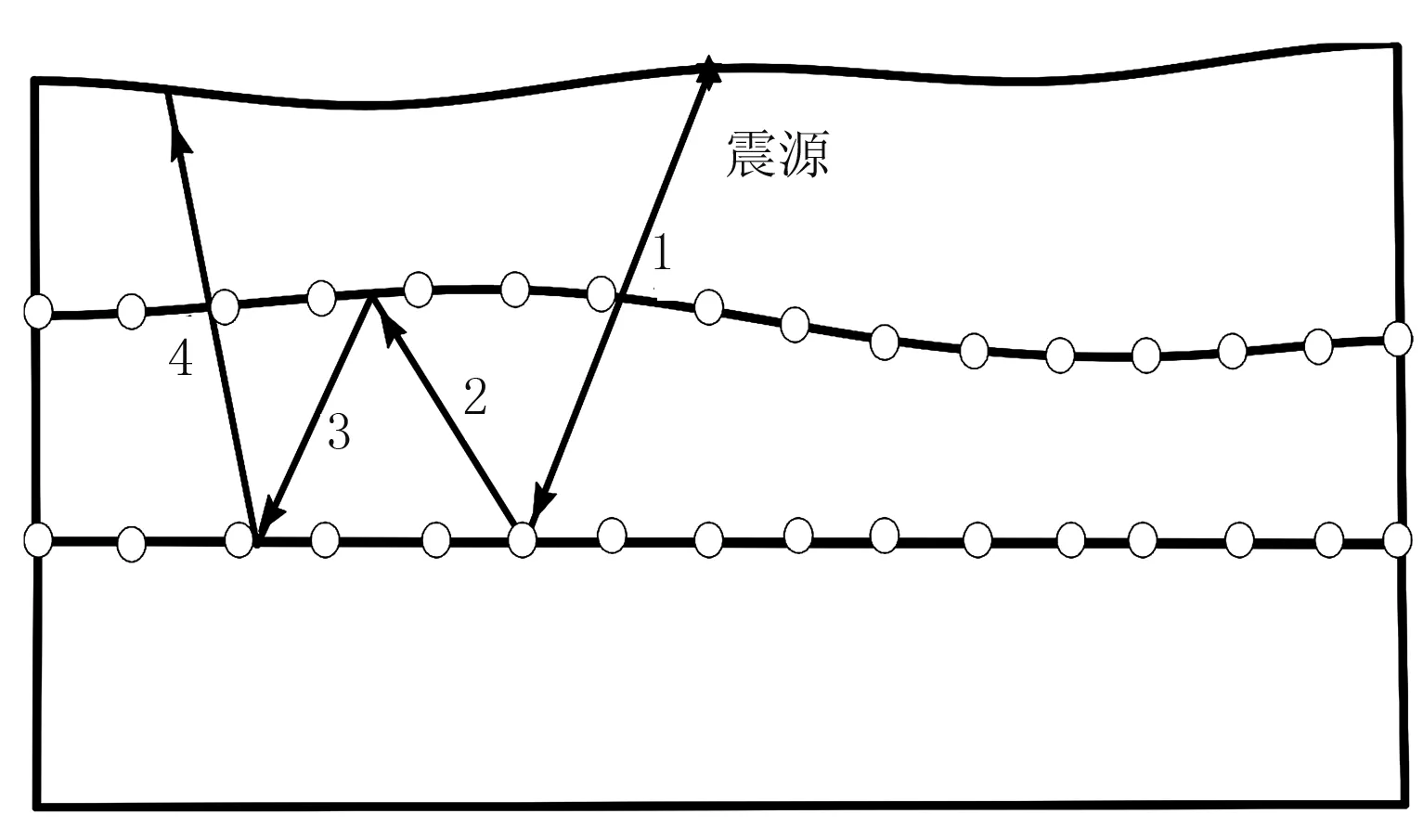
图8 二维层状介质模型多次反射、透射转换波分区示意图

2.4.2 多步计算

图9所示为反射(或反射转换)或透射(或透射转换)波的波前扩展示意图。具体实现过程为：

(1)计算由震源到第一个分区下界面的下行波的波前，并找出界面离散点上旅行时最小的点(图9a)。

(2)将(1)中计算出的旅行时最小的界面离散点作为新的震源。如果需要计算反射波的波前，则由界面上新的震源向上计算上行波在该分区内的波前(图9b)；如果需要追踪转换波，则采用转换波的速度即可计算其相应的波前。如果需要计算透射波的波前，由界面上新的震源向下计算下行波在该分区内的波前(图9c)；如果需要追踪转换波，则采用转换波的速度即可计算其相应的波前。

(3)结合(1)、(2)计算波前，可以追踪任意多次反射(或反射转换)或透射(或透射转换)波。

(4)由以上三步计算波前，再结合LTI的向后处理,追踪任意多次反射转换波的射线路径。

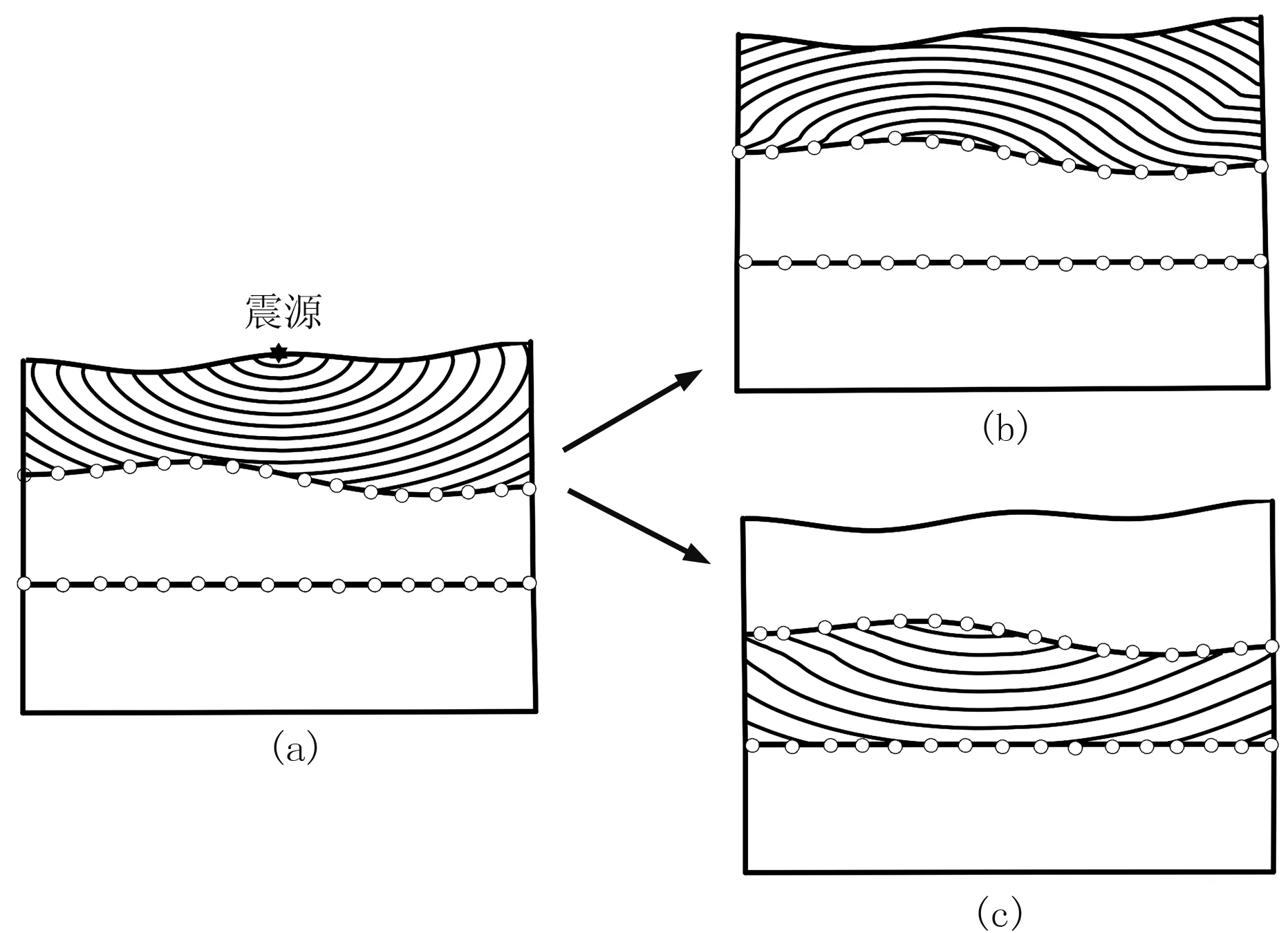
图9 波前分区扩展示意图

(a)波前由震源扩展到速度界面离散点；(b)若反射，由界面离散点旅行时计算上行波波前；(c)若透射，由界面离散点旅行时计算下行波波前

3 数值算例

首先用具有解析解的起伏地表均匀VTI介质模型检验本文算法的相对误差；然后将本文算法分别与波动方程有限差分算法、分区多步快速步进(FMM)算法和分区多步ISPM算法进行精度和效率对比；最后对带有断层的起伏层状模型进行正演模拟，验证算法对复杂模型的适应能力。

3.1 均匀VTI介质模型

VTI均匀介质模参数为：模型尺寸为400m×400m；网格尺寸为1m×1m；vP0=2700m/s；vS0=1500m/s；ε=0.15；δ=0.08；γ=0.338；ρ=2.10g/cm3。图10为在均匀VTI介质模型中三种地震波(qP、qSV 和qSH)的波前扩展过程以及三种地震波旅行时数值解与解析解的相对误差分布。

从图10a～图10c可以看出：三种地震波的各向异性效应都比较明显，且在每种地震波的传播过程中，红线(各向异性介质)与黑线(各向同性介质)总是在速度最慢的方向相切。根据式(1)可知，在各向异性介质中群速度最慢的方向的速度与在各向同性介质中是相等的；qSV与qSH的旅行时扩展特征不同，前者在对角线方向传播最快、在垂直和水平方向上传播最慢，而后者在水平方向传播最快、在垂直方向上传播最慢。从图10d～图10f可以看出,由本文方法计算的三种波的旅行时与解析解的相对误差均较小，说明算法较精确。

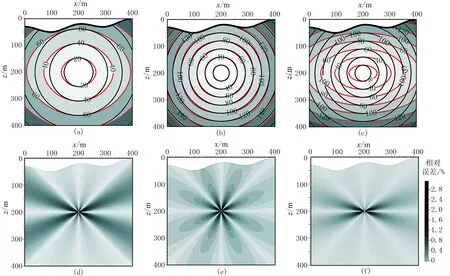
图10 均匀VTI介质模型qP波、qSV波和qSH波旅行时等值线(单位ms)及相对误差(a)、(d)qP波； (b)、(e)qSV波； (c)、(f)qSH波黑线为各向同性介质的旅行时等值线，红线为VTI介质的旅行时等值线(单位：ms)

3.2 两层水平层状模型

设计两层水平层状VTI介质模型，尺寸为1000m×1000m，各层参数如表1所示。源位于模型表面(500m，0)处。图11a和图11b分别为由本文算法和有限差分算法计算的模型表面101道接收的地震记录，道间距为10m。图11c为图11a和图11b的叠合显示，可以看出两种算法计算的初至波、反射波和转换波的记录都比较吻合，说明本文算法的计算结果比较准确。

表1 两层水平层状VTI介质模型参数

目前基于网格单元波前扩展的波前追踪方法中，较为成熟的主要有分区多步FMM算法和分区多步ISPM算法，为了验证分区多步LTI算法的计算精度和计算效率，对文献[34]的两层水平层状各向同性速度模型(表2)分别用以上三种方法、在4种网格间距下计算反射波旅行时。模型尺寸为100km×40km，地表水平，在深度30km处有一水平反射界面。在模型参数化时，分区多步FMM算法中正方形网格边长分别为1000m、500m、250m和125m；分区多步ISPM算法中网格尺寸为4km×4km，并在网格单元边界上相应加入3、7、15和31个次级节点；分区多步LTI算法中网格大小与分区多步FMM算法中设置相同。炮点在模型的左上角，100个检波器等间距(1km)排列在地面，最小炮检距为1.0km。图12和图13分别给出了随炮检距变化的分区多步FMM算法(图12a)、分区多步ISPM算法(图12b)和分区多步LTI算法(图13)相对于解析解在4种不同网格距下反射P波旅行时的相对误差。表3给出了三种方法的CPU耗时。由图12和表3可以看出，除了网格尺寸为1000m×1000m的情形外，分区多步LTI算法的精度均优于分区多步FMM和分区多步ISPM算法，在计算效率方面，分区多步LTI算法明显优于分区多步FMM算法，但低于分区多步ISPM算法。

图11 本文算法计算的地震记录(a)、波动方程有限差分法计算的地震记录(b)和二者叠合后的记录(c)对比①为初至qP波，②为初至qSV波，③为反射qP波，④、⑤为反射转换波，⑥为反射qSV波

图12 不同网格间距两层水平层状各向同性介质模型的分区多步FMM算法(a)、ISPM算法(b)反射波旅行时的相对误差(引自文献[34])

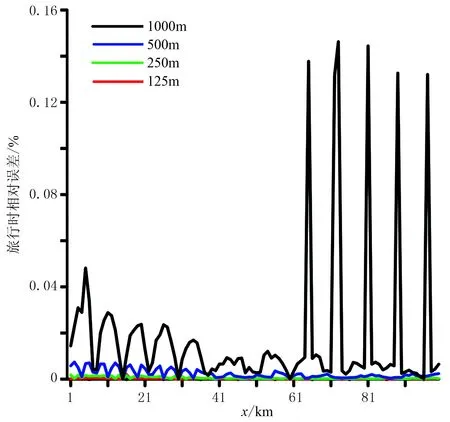
图13 不同网格间距两层水平层状各向同性介质模型的分区多步LTI算法数值解的相对误差

表2 两层水平层状各向同性介质模型参数

表3 不同网格间距分区多步FMM、ISPM

注：表中FMM和ISPM算法数据引自文献[34]

3.3 二维起伏层状VTI介质

图14a为二维起伏层状VTI介质模型的参数和分区情况。在(200m，20m)处激发，101道检波器横向均匀布设在起伏地表上。图14b～图14e为在各个分区内的各向异性介质和各向同性介质的多次反射、转换波波前扩展过程，可以看出在速度均匀的同一层内波前呈大致平行的弧线，当波前穿过速度界面时，就会随速度发生变化；同时可以看出VTI介质与各向同性介质中的波前在传播过程中总是在速度最小的方向相切，说明在各向异性介质中波前扩展方式正确。图15为图14a模型模拟的单炮合成记录，包括VTI介质qP波初至、界面Ⅰ反射qP波、界面Ⅱ反射qSH波、qSV波、VTI介质多次反射、转换波，各向同性介质P波初至、界面Ⅰ反射P波、多次反射转换波。由图15可以看出，地震波在各向异性介质和各向异性介质中传播的差异，且各向异性程度越强差异越大；在VTI介质中传播的qSV波和qSH波也有较大差异，仅在震源正下方的位置会重叠，这是因为在VTI介质的对称轴方向上qSV和qSH波的速度相同，偏离这个方向后qSH波和qSV波的各向异性效应不同。

图14 层间多次反射、透射波在各个分区中的传播过程、射线路径和单炮合成记录(波前间隔为10ms)

(a)模型参数和分区编号； (b)下行P波波前在第一个分区内传播； (c)上行SV波波前在第二个分区内传播； (d)下行P波波前在第三个分区内传播； (e)上行SH波波前在第四个分区内传播； (f)层间多次波射、转换波线路径。红色等时线和射线路径为在VTI介质中传播，黑色等时线和射线路径为在各向同性介质中传播

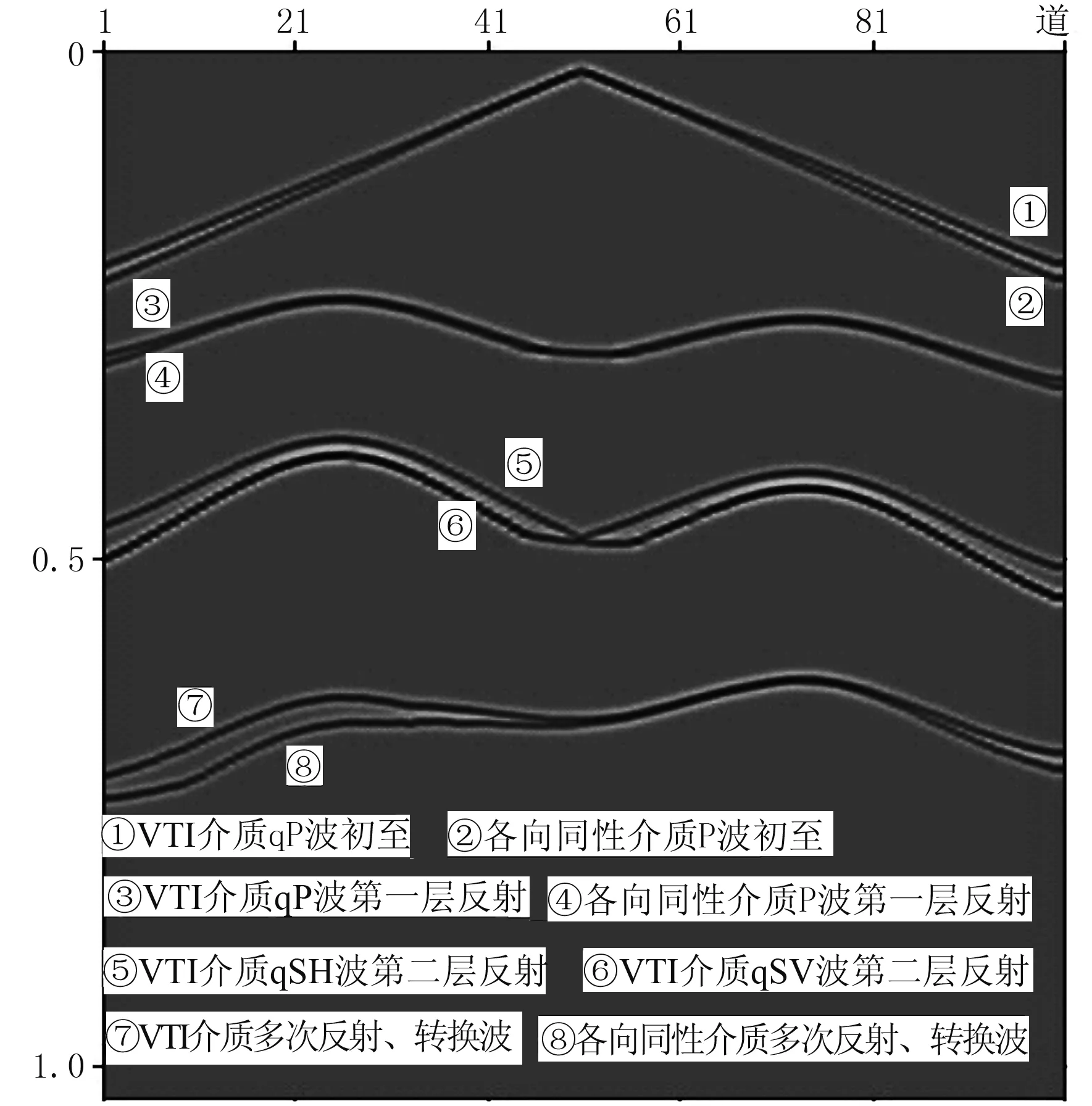
图15 单炮合成记录

4 结论

本文采用矩形网格和不规则四边形网格组成的混合网格对模型进行剖分，可以提高网格对起伏地表或界面的拟合程度，进而提高计算精度。将混合网格中群速度与群角的关系式变换成群速度与插值点坐标的关系，分别建立了针对qP、qSV和qSH波的非线性方程，并利用二分法求解，再结合分区多步计算技术，可计算VTI介质中的初至波和多种后续波的射线路径和旅行时。通过模型试算，与有限差分方法、分区多步FMM算法和分区多步ISPM算法进行对比，验证了算法效率和精度。二维起伏层状VTI介质模型结果表明，本文方法适用于复杂构造条件下VTI介质中地震波的旅行时和射线路径计算。