应用结构聚类字典学习压制地震数据随机噪声
张 岩 任伟建 唐国维
(①东北石油大学计算机与信息技术学院,黑龙江大庆 163318; ②东北石油大学电气信息工程学院,黑龙江大庆 163318; ③东北石油大学现代教育技术中心,黑龙江大庆 163318)
1 引言
随机噪声压制一直是地震资料处理中研究的热点与难点。当前地震数据随机噪声压制技术的思路是首先将地震数据稀疏表示,利用地震数据与噪声信号在稀疏域内的不同特征分离噪声,要求所采用的稀疏表示基函数能够准确地捕捉到地震波前信息,用较少的系数就可以描述这些主要特征。
地震数据稀疏表示的方法有正交变换法、多尺度几何分析法、字典学习法等。正交变换法包括Fourier变换[1]、 Radon变换[2]、Wavelet变换[3]等;多尺度几何分析法包括Ridgelet变换[4]、Curvelet变换[5]、Seislet变换[6]等。考虑到实际地震数据通常由多种元素组成,单一的固定变换基函数难以获得最优的稀疏表示效果。基于字典学习法的稀疏表示能根据地震数据本身的特点,通过对数据的学习和训练,自适应地调整变换基函数以适应特定数据本身,因此具有更好的稀疏表示能力。近年来,基于学习型字典稀疏表示的地震数据去噪技术在业内得到了广泛关注。Beckouche等[7]提出一种根据包含噪声地震数据自适应学习得到稀疏字典的去噪方法;Chen等[8]结合自适应学习字典和固定基函数的两种稀疏表示方法,提出双稀疏字典,能更好地处理去噪问题;Chen[9]以K-SVD法[10]为基础,提出多维地震数据的快速字典学习稀疏表示去噪方法;Turquais等[11]提出了基于一致性约束的字典学习去噪方法。
上述学习型字典稀疏表示方法的基本思路是:首先将地震数据分块,每一块包含多个地震记录道在一定的采样时间段内波形的信息,以地震数据块为训练样本,利用超完备字典学习技术,根据地震数据本身的特点,自适应构造超完备字典,稀疏表示地震数据,从而恢复数据的主要特征[12,13]。此类方法的共同点在于利用一个通用的字典稀疏表示整个地震数据,考虑到地震数据中不同空间位置的波形变化差异较大,通用字典不足以对整个数据的每一个局部内容都能最优地稀疏表示。在图像处理领域中,为提高稀疏表示对整个图像中局部结构的适应性,Dong等[14,15]、Xu等[16]提出自适应局部字典学习方法,利用自然图像的局部相似性,自适应得到局部字典,能够更好地刻画图像局部结构,获得更好的重构图像效果。地震数据中随机噪声普遍满足平稳性、高斯性,噪声压制算法通常可采用高斯随机噪声进行模拟仿真,更重要的是地震数据中同一反射波在相邻地震道上到达时间、振幅相近,波形相似。为利用局部数据道中同相轴振幅与波形的相似性,借鉴文献[14-16]的思想,本文提出基于结构聚类的局部超完备字典学习方法,压制地震数据中的随机噪声。
2 基于结构聚类的字典学习
2.1 全局字典稀疏表示分析
地震数据中相同颜色的分块具有相似的结构(图1),并且在地震数据中重复多次出现,说明地震数据块结构具有较强的自相似性。全局字典稀疏表示的一般模型均假设信号的稀疏表示系数之间是独立同分布。对图1地震数据利用K-SVD全局字典稀疏表示后,得到字典如图2所示,字典中原子大小为8×8,原子的数目为256。图3为图1数据对应稀疏域的系数分布结构,可见其系数分布不是完全随机的,而是具有一定的规律性与冗余性,以此作为先验知识应用到地震数据的随机噪声压制处理中,可以对地震数据进行更稳定、更稀疏的描述。

图1 地震数据块相似性(相同颜色子块具有相似的结构)

图2 K-SVD学习字典

图3 K-SVD学习字典对应的系数分布白色像素代表幅值较大的系数,黑色代表幅值较小的系数
2.2 局部字典学习模型
借鉴文献[15]的思路,利用地震数据块结构的自相似特点,提出地震数据结构聚类字典学习模型的目标函数为

(1)
式中:μk表示第k个聚类Ck的质心;Φk为第k个聚类的字典;y为无噪地震数据x的含噪结果;D为地震数据y的整体字典;α为地震数据在字典D表示下对应的系数;K为聚类的类别数目;λ1和λ2为正则化参数。稀疏系数α具有自身结构冗余的特点,对聚类质心进行更新与调整,并用各个分类的聚类质心重新编码,以得到更稀疏的系数,相当于对原始地震数据更稀疏的表示和描述。对各个聚类质心也可以采用与原始数据一样的字典进行表示,即μk=Φkβk,其中βk代表μk在字典Φk下的系数。受L1范数下的压缩感知理论启发,可用L1范数代替L2范数,将式(1)优化为

(2)
上式利用地震数据的自相似性与稀疏系数结构冗余性,将字典学习和结构分类统一起来。βk可以看成是通过结构分类所获得聚类中心而得到的新编码,依照先验知识不断促进系数的稀疏程度。
2.3 结构聚类方法
地震数据块结构聚类的过程无需关心某一类的特征,仅需将相似的地震数据块聚为一类,因此不需要对训练数据进行学习,即为无监督学习的过程。典型的聚类算法主要包括:属于划分法的K均值聚类算法[17]、K中心点算法[18]、Clarans算法[19];属于层次法的Birch算法[20]、Cure算法[21]、Chameleon算法[22]等;基于簇密度的Dbscan算法[23]、Optics算法[24]、Denclue算法[25]等;基于网格的Sting算法[26]、Clique算法[27]、Wave-Cluster算法[28]等。由于K均值聚类算法计算效率高,在对大规模数据聚类时被广泛应用。利用K均值聚类算法对地震数据分块结构聚类的关键环节有3个。①初始质心的选取:适当的初始质心是基本K均值聚类算法的关键。为提高计算效率,本文利用随机选择地震数据块的方式作为初始质心。每次运行过程中,在地震数据的分块中使用一组不同的随机初始质心,然后选取具有最小误差平方和的簇集作为质心。该策略计算效率高,效果相对好。②度量距离的选择:聚类采用的距离度量方法(相似性度量方法)有很多种,常用的有欧氏距离、闵可夫斯基距离、曼哈顿距离、皮尔逊相关系数、余弦相似度等。余弦相似度更多地是从方向上区分差异,对绝对的数值不敏感。本文重点关注地震数据各个分块的结构相似情况,因此采用余弦相似度作为距离的度量。③质心的计算:在K均值算法中,将簇中所有地震数据样本块的均值作为该簇的质心,即向量各维取平均作为新的质心。
2.4 字典学习方法
文献[10]中字典学习采用主成分(PCA)分解提取主成分,虽然在构造的字典中各个原子满足正交条件,计算效率相对高,但是直接将该算法应用于地震数据的去噪存在一定的局限性,原因在于地震数据中相当一部分中、高频信息比较重要,去噪过程应该注意保留,同时对地震数据PCA分解需要计算协方差矩阵,对于某些矩阵求协方差时很可能会损失精度,更重要的是冗余度较大的超完备字典更有利于地震数据细节的保留,因此本文对每一类数据块采用奇异值分解构造超完备字典,稀疏编码该类地震数据。
2.5 模型求解算法
针对式(2)目标函数的最大后验概率估计问题为
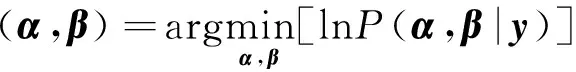
(3)
根据贝叶斯公式将式(3)改写为

(4)
式中:前一项对应于原目标函数中的误差项;后一项为先验概率项。由于观测模型采用的是加性高斯噪声模型,并且用独立同分布的拉普拉斯分布函数描述α,最终可得
(5)
式中:σ1和σ2分别为式(4)中两项的标准差;σn为噪声标准差。则有
(6)
从上式可以发现,实际上对各个稀疏系数局部方差的估计,可以从输入数据自适应得到正则项系数的估计值。通过估计每一类系数的正则化参数,获得实际地震数据的逼近,然后再利用逼近的地震数据更新正则化参数的估计,依此不断迭代,最终收敛获得最优的地震数据逼近值。在字典确定的情况下,对于上述目标函数需要求解模型中双L1范数的优化问题,即需要联合求解α和β,然而这是一个非凸的优化问题,无法通过线性规划方法求解,可采用交替迭代的优化方法求解,即先固定待求量中的一个,对另一个待求量进行优化; 再固定己经优化了的待求量转而对另一个待求量进行优化,两步交替迭代进行,直到目标函数收敛。在稀疏系数α的聚类中心β确定的情况下,本文采用双变量迭代阈值算法,交替更新α和β。借鉴替代函数的思想[29],更新α
(7)
式中:Sτ1,τ2为迭代收缩算子;αj,t和βj,t分别代表向量αj和向量βj中的任意一个元素;
(8)
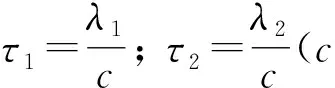
(9)
其中c1与c2是两个给定的常数。
受文献[32]的启发, 通过下式更新恢复地震数据
(10)
其中
(11)
上式是实现迭代正则思想的算子,ω是一个控制迭代反馈的噪声级小正数。
本文提出的基于结构聚类超完备字典地震数据去噪算法,通过K均值聚类算法和奇异值分解得到字典Φ与稀疏系数α;然后迭代更新正则化参数,更新质心估计β和地震数据估计值,最后输出去噪后的地震数据,具体算法流程如图4所示。

图4 本文算法流程
3 实验结果与分析
实验过程中,设置每一个地震数据块大小为8×8,相邻数据块之间的间隔设为2,初始化采用离散余弦基构造超完备字典,结构聚类数目为40,字典学习次数为5,结构聚类次数为5。地震数据去噪效果的衡量指标采用峰值信噪比(RSNR),其表达式为
(12)
式中RMSE为不含噪声原始数据与去噪后数据的均方误差,定义为
(13)
式中:N为时间样点数;M为地震记录道数。为了模拟地震数据中包含的随机噪声,本文在原始地震数据中加入零均值正态分布的高斯随机噪声,噪声的标准差与原始地震数据的标准差呈正相关。噪声标准差定义为
(14)

3.1 合成地震数据实验分析
图5a是合成原始单炮地震记录,道数为140,样点数为287;图5b为加入噪声强度比例因子为0.03的高斯随机噪声单炮记录,其RSNR为30.42dB。图6a为本文算法去噪后结果,RSNR为39.53dB,约提高了9dB,且地震数据的同向轴方向性与连续性保持较好;图6b为K-SVD算法的去噪结果,RSNR为35.99dB,可见本文算法结果具有较高的RSNR,而且压制随机噪声的效果更好。图6c是本文算法去噪结果与原始数据差值,图6d为本文算法结果的RSNR随迭代次数的变化曲线,说明本文算法具有较高的稳定性和有效性。

图5 合成原始单炮记录(a)及其加噪记录(b)

图6 合成地震数据实验(a)本文算法随机噪声压制结果; (b)K-SVD算法随机噪声压制结果; (c)本文算法去噪结果与原始数据的差值; (d)本文算法结果的RSNR随迭代次数的变化曲线
图7a是5次聚类过程中质心变化的图示,按由上至下的顺序分别给出聚类1~5次的质心块集合,由于聚类数目为40,因此每一行包括40个质心块,随着聚类次数的增加,特征类似的质心块逐渐减少,不同类别质心之间的差异逐渐明显,表明聚类算法设计合理有效。图7b为40个分类的地震数据块,经过5次迭代后训练得到的字典,字典中的每列为一类数据块的局部字典,每类的字典包括64个原子,每个原子大小为8×8,可以看出每一类数据块对应的局部字典中原子存在一定的冗余度,保证了对地震数据更完备的描述。

图7 聚类质心变化(a)和超完备局部字典(b)
为分析聚类数目对算法效果的影响,图8a给出了运行时间随聚类数目的变化曲线,可见当聚类数目的增加,算法运算量逐渐增加,导致运行时间增加。图8b给出了去噪结果的RSNR随聚类数目的变化曲线,表明对于该合成地震数据,在聚类数目为5时,算法具有最高的去噪效果,当聚类数目超过5时,随着聚类数目的增加,RSNR有下降趋势,说明不同的聚类数目参数会影响算法整体的运行时间与效果。
3.2 Marmousi模型地震数据实验分析
在Marmousi数据模型中随机抽取单炮数据,截取原始地震数据207道,每道700个采样点(图9a),加入噪声强度比例因子为0.03的高斯随机噪声数据(图8b),RSNR为30.46dB。使用该数据进行本文算法与小波变换、曲波变换及K-SVD算法的效果对比。图10a为小波变换去噪结果,小波基采用db5,分解级数为5,去噪之后噪声得到一定的压制,其RSNR为32.74dB;图10b为Curvelet变换去噪结果,Curvelet分解级数为5,由于Curvelet具有较好的方向性,去噪效果相对较好,RSNR为33.66dB。图10c为K-SVD字典法去噪结果,初始化采用离散余弦基构造超完备字典,以可重叠的8×8固定大小的数据块为单位,构造的超完备字典可捕捉整体目标数据的主要特征,逼近原始数据,RSNR为33.84dB;图10d为本文算法去噪结果,由于采用了结构聚类字典学习的思想,对原始数据进行分类稀疏表示后,提高了去噪效果,RSNR为38.43dB。

图8 运行时间(a)及RSNR(b)随聚类数目的变化曲线
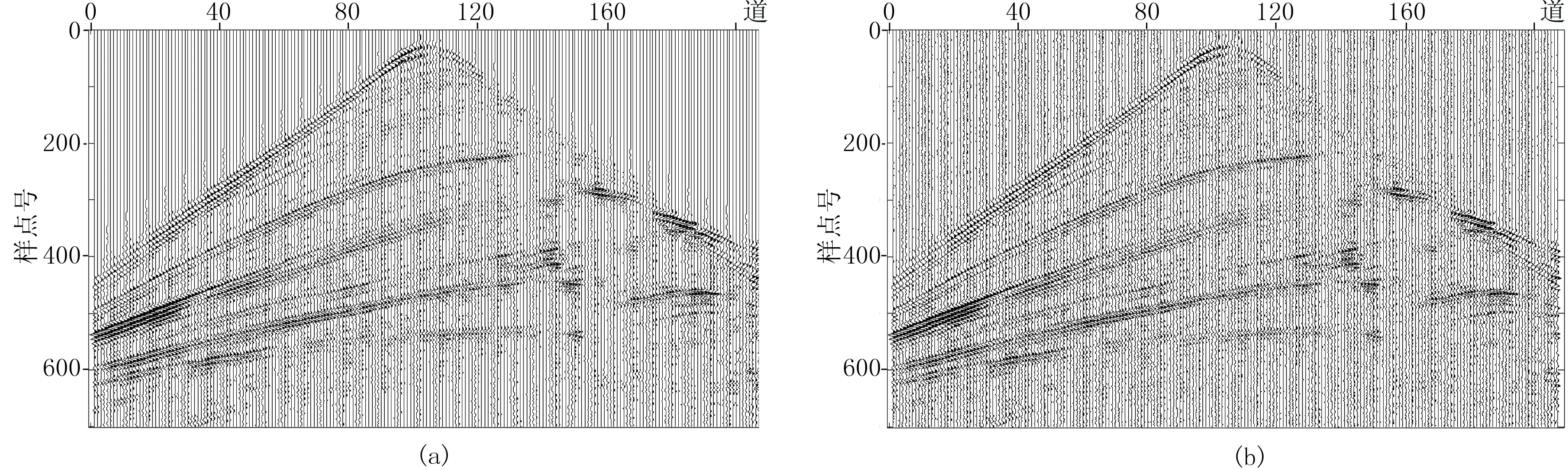
图9 Marmousi模型合成单炮数据(a)及其加噪结果(b)
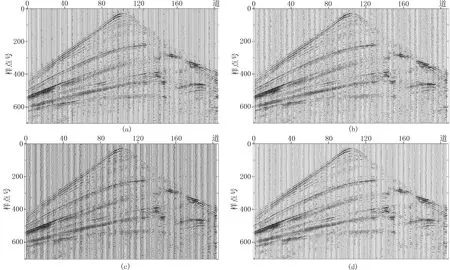
图10 Marmousi模型数据不同方法随机噪声压制效果(a)小波变换法; (b)Curvelet变换法; (c)K-SVD字典法; (d)本文算法
为测试本文算法对不同强度高斯随机噪声的敏感程度,表1分别给出了小波变换法、Curvelet变换法、K-SVD自适应学习字典法及本文算法在不同强度随机噪声下的去噪效果(RSNR)对比。从表1可以看出,随着加入高斯随机噪声的标准差从地震数据标准差的0.01增加到0.08,去噪的难度逐渐增加,各个算法的去噪效果变差,相比之下本文算法在各个噪声强度下均能取得最好的去噪效果。

表1 不同算法在加入不同强度高斯随机噪声下噪声压制后的RSNR(单位:dB)对比
3.3 实际地震数据实验分析
图11为M区原始叠后海洋地震数据片段,其中道数为300、样点数为500。图12a为小波变换去噪结果,RSNR=23.16dB; 图12b为Curvelet变换去噪结果,RSNR=24.42dB; 图12c为K-SVD字典学习法的去噪结果,RSNR=24.53dB; 图12d为本文算法的去噪结果,RSNR=25.25dB。由此可见本文算法利用地震数据结构聚类字典学习的思想,在地震数据同向轴连续区域,能够较好地提取出地震数据的主要特征,稀疏表示地震数据,压制随机噪声(如矩形框所示)。但在地震波能量较弱的区域,由于原始地震数据波前曲线特征不明显,地震数据与噪声数据振幅相当的情况下,地震数据稀疏表示的能力受到影响,存在细节丢失的现象(如椭圆区域所示)。

图11 实际地震剖面

图12 实际数据不同方法噪声压制结果对比(a)小波变换法; (b)Curvelet变换法; (c)K-SVD字典法; (d)本文算法
4 结论
为提高超完备字典学习方法对地震数据的稀疏表示能力与去噪效果,本文提出结构聚类字典学习稀疏表示的地震数据去噪方法。通过理论分析与模型实验可以得出以下结论:
(1)利用结构聚类字典学习可以提高地震数据稀疏表示的能力,减少全局字典稀疏表示系数的冗余程度,有利于地震数据去噪处理;
(2)基于结构聚类字典学习的去噪算法效果和运行时间受聚类数目参数影响较大,当聚类数目与实际地震数据分块类别接近时,去噪效果较好,而运行时间随聚类数目增加而增加;
(3)本文算法对地震数据中能量弱的局部区域去噪会出现细节丢失的现象,该问题是今后重点改进的研究方向。

