预测铣削稳定性的Hamming线性多步法

智红英 ， 闫献国， 杜 娟， 曹启超

(1.太原科技大学 应用科学学院, 太原 030024； 2.太原科技大学 机械工程学院, 太原 030024)

在高速精密铣削加工过程中，再生颤振是一种常见的自激振动现象[1-2]，是引起加工过程失稳的主要因素[3]。因此，为了防止铣削加工过程中再生颤振的发生，加工前需要对铣削稳定性进行预测，以便在加工时获得较高的表面质量，从而提高零件的精度。此外，考虑到再生颤振的铣削动力学模型可以近似地表示为时滞微分方程[4-5]，所以如何求解时滞微分方程才能精确且快速地获得稳定性叶瓣图是预测铣削稳定性的关键。

迄今为止，预测铣削稳定性的方法有很多种，主要分为实验方法和数值方法，而数值方法主要有频域法和时域法两种。Budak等[6-7]提出了一种近似零阶的半解析方法的频域法求解铣削动力学方程，但这种方法无法满足小径向切深切削的计算精度。为了解决这个问题，Merdol等[8]提出了一种可以满足小径向切深的多频域法。随后，Insperger等[9-11]用时域法预测颤振稳定性，即半离散法(SDM)。该方法对铣削时滞微分方程中延迟项进行离散，其计算精度取决于离散步长。

基于这种方法，龙新华等人考虑了刀具与工件之间接触效应的损失[12]和切削厚度变化相关的时间延迟效应[13]，李中伟等[14]提出了基于Magnus-Gaussian 截断的铣削系统稳定性的改进的半离散法，Magnus-Gaussian截断法比零阶半离散法的收敛速度更快、计算时间更短。Butcher等[15-16]提出了Chebyshev多项式法和基于Chebyshev配点法来预测具有线性时滞微分方程铣削过程稳定性。为了提高计算精度和计算效率，Ding等[17-18]提出了全离散方法(FDM)，包括一阶全离散法(1st-FDM)和二阶全离散法(2nd-FDM)，这种方法是通过线性插值对状态项和延迟项进行离散化处理。随后，Guo等[19]在此基础上通过牛顿插值提出了三阶全离散法(3rd-FDM)，得出了具有比一阶、二阶全离散法更高的计算精度和更快的计算效率。Li等[20]提出了一种完全离散算法，这种方法是针对铣削稳定性预测的一种半解析算法。与半离散算法(SDM)和全离散算法(FDM)相比，此算法对时滞微分方程的各个部分都进行了离散化处理，简化了离散化后迭代方程的复杂度。为了精确分离刀具自由振动时段和刀具-工件接触过程中的强迫振动时段，Bayly等[21]提出了时域有限元分析方法，并具有较高的计算精度。Ding等[22]提出了一种数值积分法，这种方法是基于牛顿-柯特斯公式和高斯公式，通过直接离散积分方程中的积分项，构造出系统在单周期上的Floquet转移矩阵用于预测铣削稳定性。Ding等[23]随后又将有关数值积分法扩展为谱方法。在数值积分方法思想的指导下，Niu等[24]提出了一种广义的龙格库塔方法预测具有再生颤振的铣削稳定性。Li等[25]在经典的四阶龙格库塔的基础上，基于完全离散法，提出了一种完全离散化的龙格库塔方法预测铣削稳定性。Zhang等[26]基于辛普森公式提出了一种全新的方法预测铣削稳定性。Qin等[27]提出了一种基于亚当斯-莫尔顿的线性多步法预测铣削稳定性。Zhang等[28]根据泰勒公式，运用有限差分法和外推法，提出了一种数值微分法预测铣削稳定性。

随着研究的不断深入，越来越多的方法被用于预测铣削过程的稳定性。针对铣削加工动力学方程，提出了一种Hamming线性多步法预测铣削稳定性。

2 动力学模型

通过考虑再生颤振的动力学模型预测铣削稳定性，其动力学模型可由以下时滞微分方程描述：

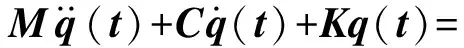
(1)

式中:M，C和K分别表示刀具的模态质量、模态阻尼和模态刚度矩阵；q(t)为刀具模态坐标，Kc(t)为周期系数矩阵，ap为轴向切削深度，T为时滞量且等于刀齿切削周期，T=60/(NΩ),N为刀具齿数，Ω为主轴转速，单位为r/min。

令

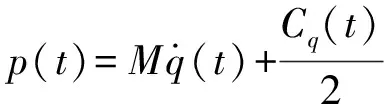
(2)

式(2)中，A0表示常数矩阵；A(t)表示周期为T的考虑再生效应的系数矩阵，且A(t)=A(t+T)。其中

(3)

单自由度和两自由度系统主要区别是状态向量x(t)、常数矩阵A0和周期矩阵A(t)的不同，下面将主要介绍这两种动力学模型。

1.1 单自由度动力学模型

具有x方向的单自由度铣削加工动力学模型可由下列方程表示：

(4)

式中:mt,ζ,ωn分别表示刀具的模态质量、刀具的阻尼比、自然圆频率；ap为轴向切削深度；T为时滞量且等于刀齿切削周期，即T=60/(NΩ)。h(t)由下列方程表示：

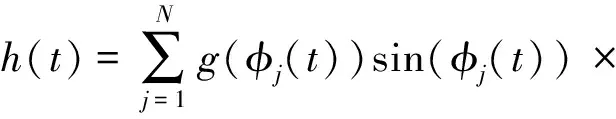
(5)

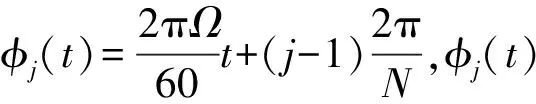
(6)

式中:φst和φex分别表示刀具的切入角和切出角。对于顺铣，φst=arccos(2a/D-1),φex=π; 逆铣时，φst=0,φex=arccos(1-2a/D), 其中a/D表示为径向切深与刀具直径之比。

(7)

式(7)中

(8)

1.2 双自由度动力学模型

在x和y方向上的双自由度铣削动力学模型可由下列方程表示：

(9)

式(9)中周期系数矩阵Kc(t)可表示为：

(10)

其中：

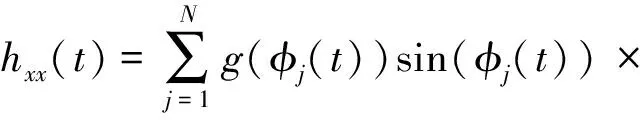
(11)

(12)

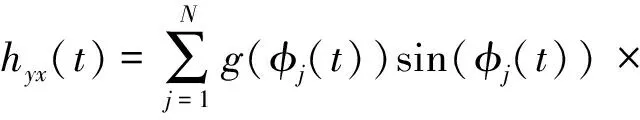
(13)

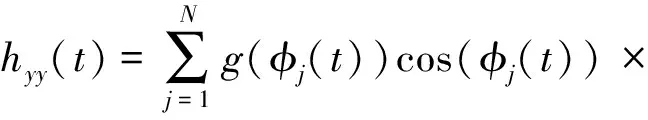
(14)

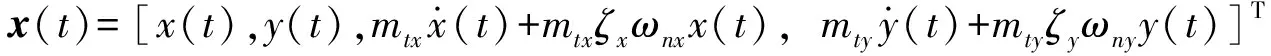
(15)

其中：

(16)

(17)

2 Hamming线性多步法(HAMM)

假设初始时刻为t0，通过空间状态变换理论[17-18]，式(1)的解可由如下方程表示：

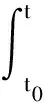
(18)

刀齿切削周期T可以划分为自由振动时间间隔和tf强迫振动时间间隔T-tf。当刀具处于自由振动时刻t时，即t∈[t0,t0+tf]，状态值有如下关系：

x(t)=eA0(t-t0)x(t0)

(19)

加工时刀具处于强迫振动时刻t时，即t∈[t0+tf,T], 将切削时间T-tf平均分成m个时间间隔，则每个时间间隔可表示为h=(T-tf)/m，相应的离散点表示为

ti=t0+tf+(i-1)h,i=1, 2, …,m+1

(20)

当t∈[ti,ti+1]时，方程(18)可以转化为如下表达式：

(21)

t=t1时，代入(19)式可得状态量x(t1)和时滞量x(tm+1-T)之间的关系如下式表示：

x(t1)=x(t0+tf)=eA0·tfx(t0)=eA0·tfx(tm+1-T)

(22)

其余离散点x(ti)(i=2, …,m+1)可以通过线性多步法进行求解，为了简化表达式，将A(ti)表示为Ai，x(ti)表示为xi，x(ti-T)表示为xi-T。

x2和x3利用Adams线性多步法[27]可以表示为：

(23)

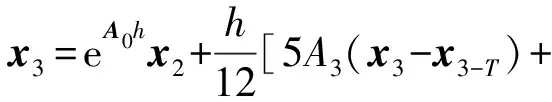
(24)

对式(23)、(24)分别化简可得：

(25)

(26)

对于xi(i=4, 5, …,m+1)，用线性多步法中的Hamming公式来进行求解，则可表示为：

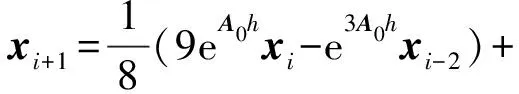
(27)

式(27)整理可得：

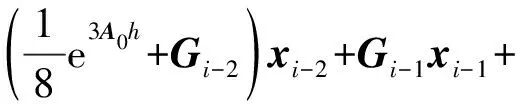
(28)

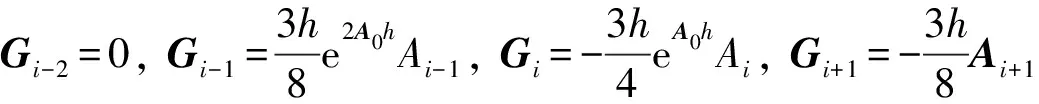
联立式(22), (25), (26), (28)可得：

(29)

其中：

(30)

(31)

通过Hamming方法(HAMM)求得系统的状态传递矩阵Φ为：

Φ=P-1Q

(32)

根据Floquet理论，当系统传递矩阵Φ特征值都小于1时，系统处于稳定状态，否则，该系统则会进入颤振状态。

3 数值仿真结果分析

3.1 收敛性分析

局部离散误差的变化可以反映所提出方法收敛速度的快慢程度。通过理论上对局部离散误差的分析，1st-SDM[10]和2nd-FDM[18]的局部离散误差均为O(h3)，HAMM的局部离散误差为O(h5)。利用Matlab软件编程，在单自由度铣削动力学模型下对1st-SDM、2nd-FDM和HAMM三种方法的收敛性进行分析。切削参数为：径向比a/D=1，切向力系数Kt=6×108N/m2，法向力系数Kn=2×108N/m2, 主轴转速Ω=10 000 r/min和5 000 r/min，轴向切削深度ap==1.5 mm、1 mm、0.3 mm。模态参数采用与文献[10]一样的参数：逆铣，刀具齿数N=2，模态质量mt=0.039 93 kg，固有圆频率wn=922×2π rad/s，固有阻尼ζ=0.011。

在1st-SDM、2nd-FDM和HAMM中，分别计算一个刀齿周期下不同离散数m所对应的状态传递矩阵临界特征值的模|μ|，局部离散误差||μ|-|μ0||，而精确值|μ0|是m=500时采用1st-SDM得到的特征值的模。不同转速和不同轴向切削深度下，1st-SDM、2nd-FDM、HAMM三种方法所对应的局部离散误差如图1所示。

由图1可知，在不同的主轴转速和轴向切削深度下，随着离散数m的不断增加，三种方法的局部离散误差越来越接近于0。在离散数相同的条件下，HAMM的局部离散误差要远远小于1st-SDM和2nd-FDM。

比如主轴转速Ω=10 000 r/min，|μ0|=1.336 4 r/min，m=50时，1st-SDM的局部离散误差为0.011 72，2nd-FDM的局部离散误差为0.005 16，HAMM的局部截断误差为0.001 28，1st-SDM的局部离散误差减少89%，比2nd-FDM的局部离散误差减少75%。

此外还可以明显地看出，HAMM的收敛速度均快于其它两种方法，主轴转速越高，离散数少的HAMM能达到离散数较多的1st-SDM和2nd-FDM的局部离散误差，和理论分析结论一致。因此，在相同的局部离散误差下，HAMM计算所用的时间远远少于1st-SDM和2nd-FDM。

图1 1st-SDM、2nd-FDM、HAMM三种方法收敛速度的比较Fig.1 Convergence rate comparisons of1st-SDM, 2nd-FDM and HAMM

3.2 稳定性叶瓣图

3.2.1 单自由度铣削模型

在单自由度铣削模型中，为了比较1st-SDM、2nd-FDM和HAMM这三种计算方法的准确性，将模态参数设置与2.1节相同。径向比a/D=1, 0.1, 0.05，主轴转速为5 000≤Ω≤10 000 r/min，并设置200个等间距的转速；轴向切削深度0≤w≤10 mm，并设置100个等间距切削深度，则铣削稳定性叶瓣图便构成了200×100的网格。设离散数m为30、40，通过2.1节可知，HAMM计算速度快，具有较高阶的误差，故将HAMM离散数m=200时所得的稳定性叶瓣图作为理想参考曲线。在不同离散数值和不同径深下，三种方法所得的稳定性叶瓣图与理想参考曲线的对比如图2～4所示。

由图2～4可知，在单自由度铣削模型下，在同种方法中，随着离散数m的增加，三种方法的计算精度都有所提高，都更接近理想参考曲线，当离散数m相同时，HAMM的计算精度要优于1st-SDM和2nd-FDM的计算精度。

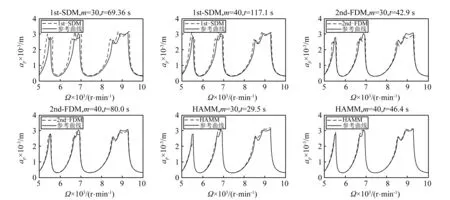
图2 单自由度铣削模型a/D=1下1st-SDM、2nd-FDM、HAMM三种方法的稳定性叶瓣图Fig.2 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=1

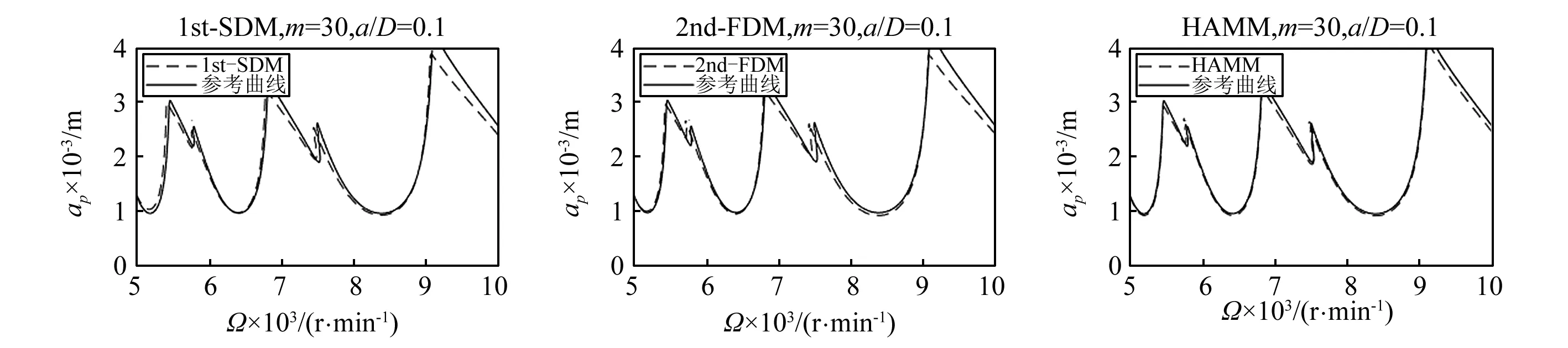
图3 单自由度铣削模型a/D=0.1下1st-SDM、2nd-FDM、HAMM三种方法的稳定性叶瓣图Fig.3 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=0.1

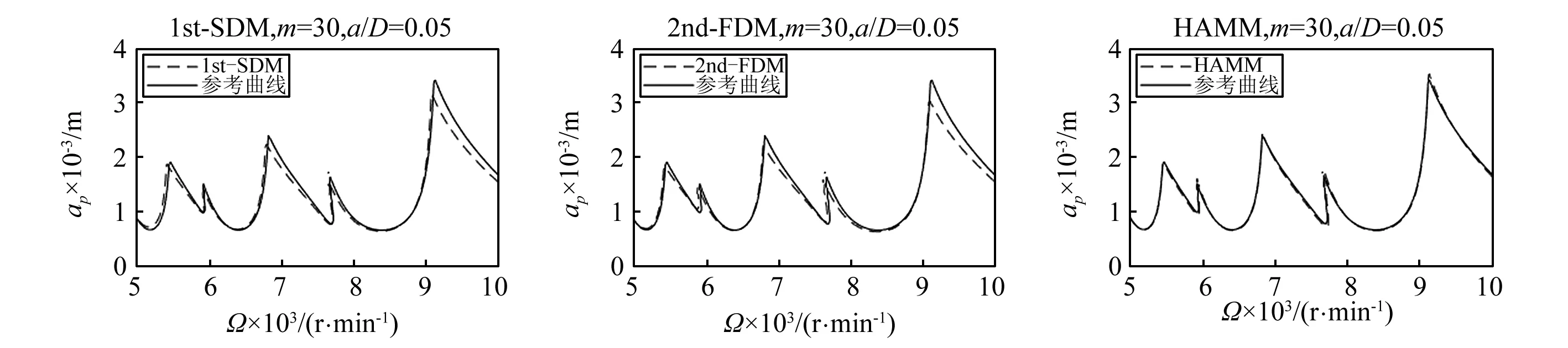
图4 单自由度铣削模型a/D=0.05下1st-SDM、2nd-FDM、HAMM三种方法的稳定性叶瓣图Fig.4 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=0.05

在图2中，当m=30时，1st-SDM的计算时间为69.36 s，2nd-FDM的计算时间为42.9 s，HAMM的计算时间为29.5 s，比1st-SDM所用时间缩短57.6%，比2nd-FDM所用时间缩短31.2%。当m=40时，1st-SDM的计算时间为117.1 s，2nd-FDM的计算时间为80 s，HAMM的计算时间为46.4 s，比1st-SDM所用时间缩短60.3%，比2nd-FDM所用时间缩短42%。

在图3，图4中可以看出，在离散数m相同时，当径向比a/D比较小时，HAMM方法计算精度远远高于1st-SDM和2nd-FDM。故HAMM是一种较优的预测铣削稳定性的计算方法。

3.2.2 双自由度铣削模型

双自由度铣削过程的系统参数与单自由度的参数相同。设刀具浸入比a/D=0.1，离散数m=10和20，主轴转速Ω从5 000 r/min到20 000 r/min，轴向切削深度ap从0～10 mm，稳定性叶瓣图的网格设置为200×100，将m=200时由HAMM进行数值计算得出的稳定性叶瓣图作为理想参考曲线，三种方法的稳定性叶瓣图与理想参考曲线的对比图，如图5所示。

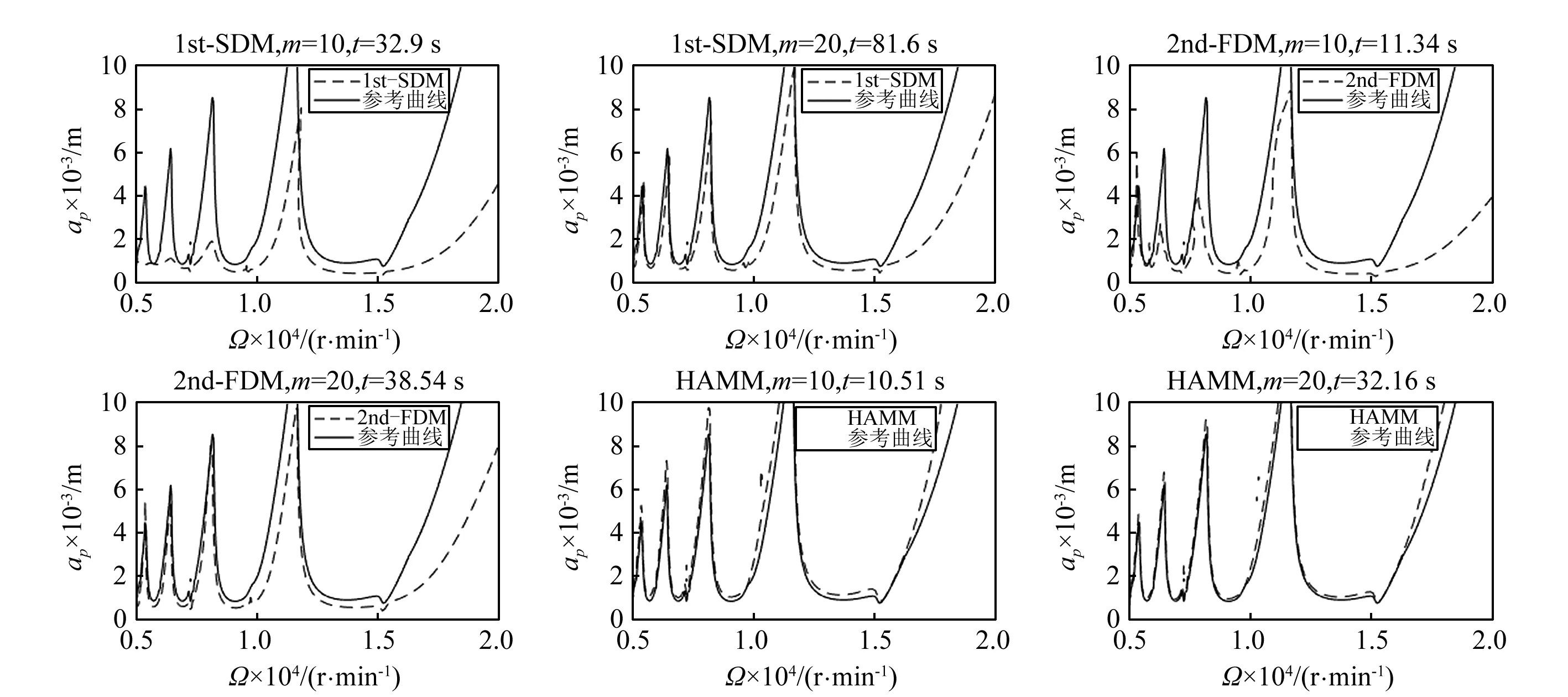
图5 双自由度铣削模型下1st-SDM、2nd-FDM、HAMM三种方法的稳定性叶瓣图Fig.5 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a double degree-of-freedom milling model

由图5可以看出，在同种方法中，随着离散数的增加，三种方法的计算精度都有所提高；当离散数m相同时，HAMM的计算精度远远高于1st-SDM和2nd-FDM。举个例子来说，当m=10时，1st-SDM的稳定性叶瓣图和理想参考曲线间产生了明显的偏差，2nd-FDM的稳定性叶瓣图虽然降低了和参考曲线间的偏差，但还是存在明显的不同之处，而HAMM的稳定性叶瓣图几乎和理想参考曲线一致。

当m=10时，1st-SDM的计算时间为32.9 s，2nd-FDM的计算时间为11.34 s，HAMM的计算时间为10.51 s。当m=20时，1st-SDM的计算时间为81.64 s，2nd-FDM的计算时间为38.54 s，HAMM的计算时间为32.16 s，因此，在离散数相同时，HAMM的计算效率和2nd-FDM相当，远远高于1st-SDM。故HAMM是一种具有较高的计算精度和较快的计算效率的预测铣削稳定性的方法。

4 实验验证

针对提出的用于预测铣削稳定性的HAMM算法，本节通过实验来进行验证。本次验证实验所用机床为五轴立铣加工中心DMU60monoBLOCK,所用铣刀为整体式硬质合金4刃刀具，直径为12 mm，刀长为75 mm。被加工工件材料为航空铝合金AL7075,实验采用无冷却液的干式切削。试验现场，如图6所示。

图6 试验现场Fig.6 Testing site

在切削铝合金工件的过程中，切削参数为：径向比a/D=1，切向力系数Kt=6×108N/m2，法向力系数Kn=2×108N/m2，主轴转速为3 000 r/min，3 500 r/min，4 000 r/min，4 500 r/min和5 000 r/min，轴向切削深度为0.4 mm，0.8 mm，1.2 mm，1.6 mm，2.0 mm。模态参数由模态锤击试验获得：逆铣，刀具齿数N=4，模态质量mt=0.1 kg，固有圆频率ωn=9 420 rad/s，固有阻尼比ζ-0.029 81。

选用不同的主轴转速和轴向切削深度进行切削，利用激光测振仪搜集振动信号，并利用统计方法进行分析得稳定点和不稳定点。基于HAMM法预测铣削稳定性的有效性,结合实验参数,计算机仿真结果和试验结果，如图7所示。

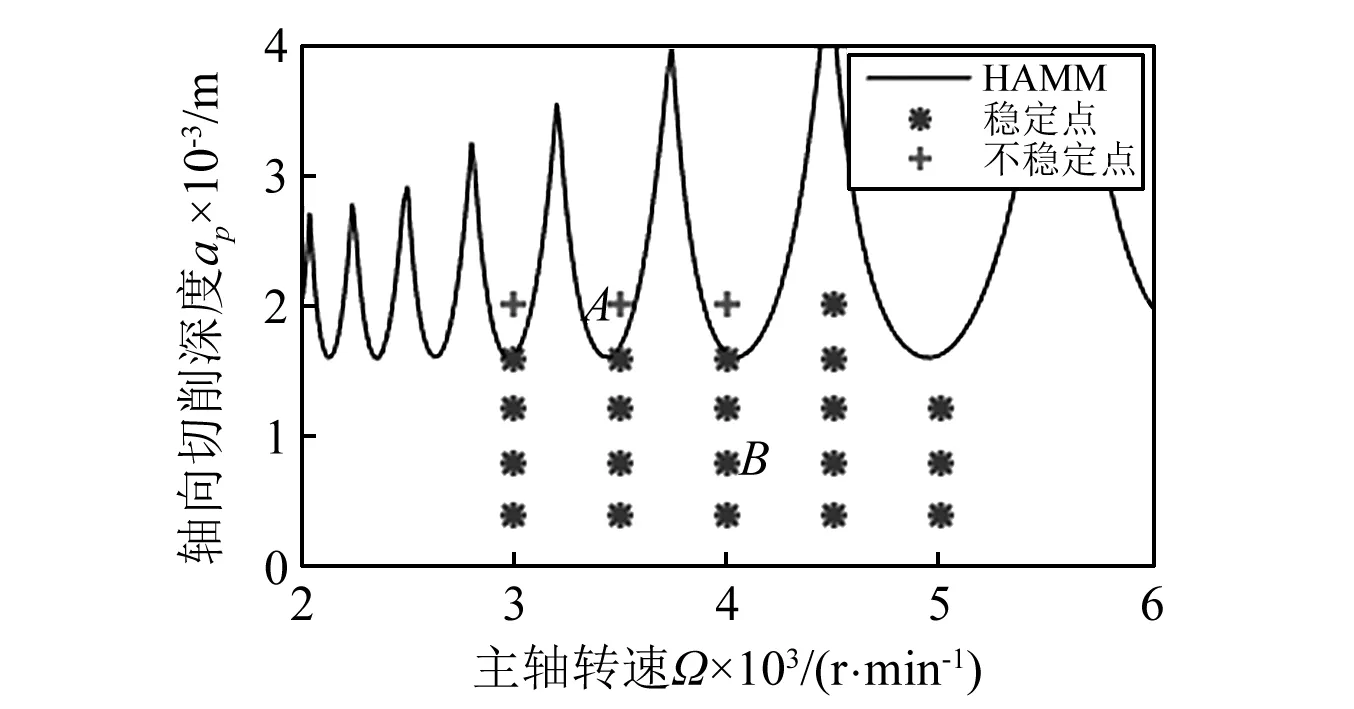
图7 HAMM法的计算机仿真结果和实验结果Fig.7 Computer simulation and experimental results of HAMM method

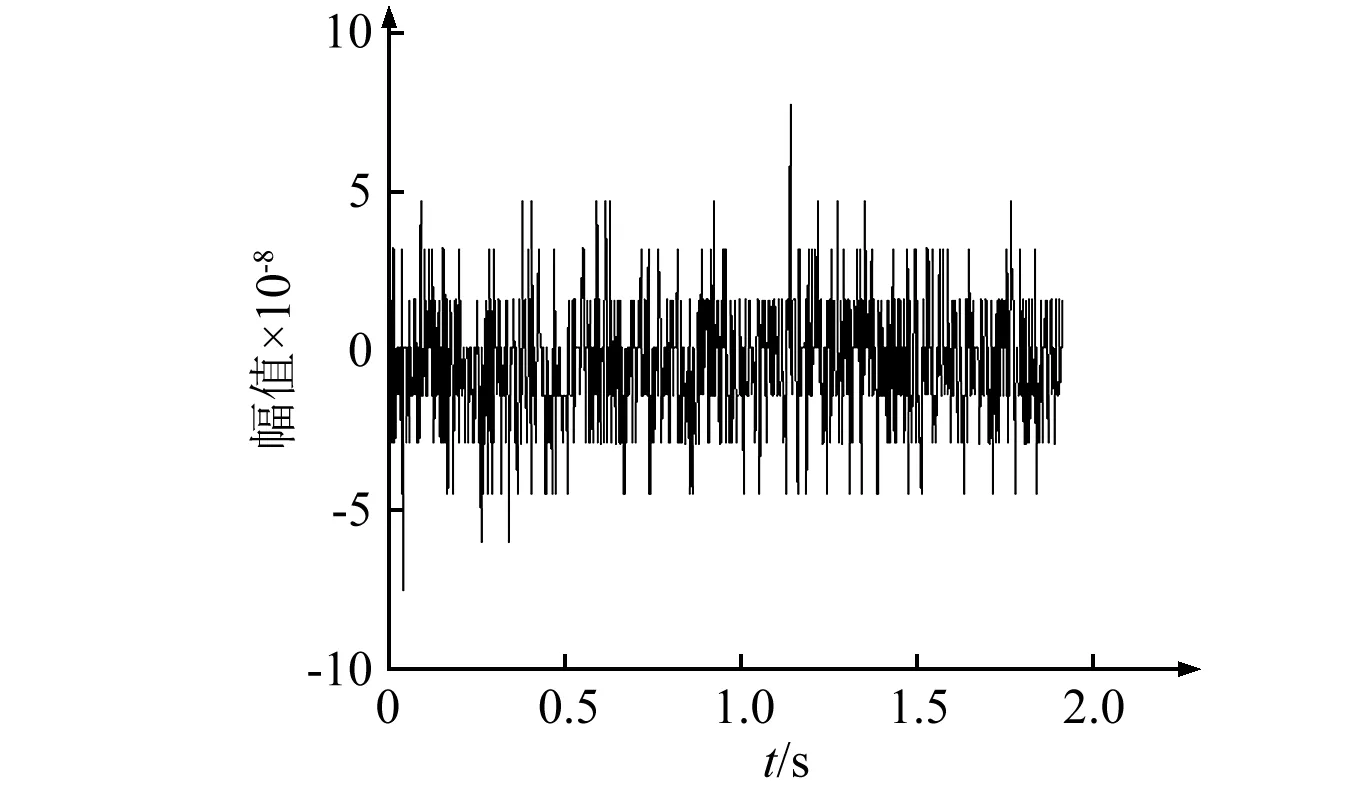
图8 稳定点B的时域图Fig.8 Time-domain diagram of stability point B

稳定点B的时域图如图8。

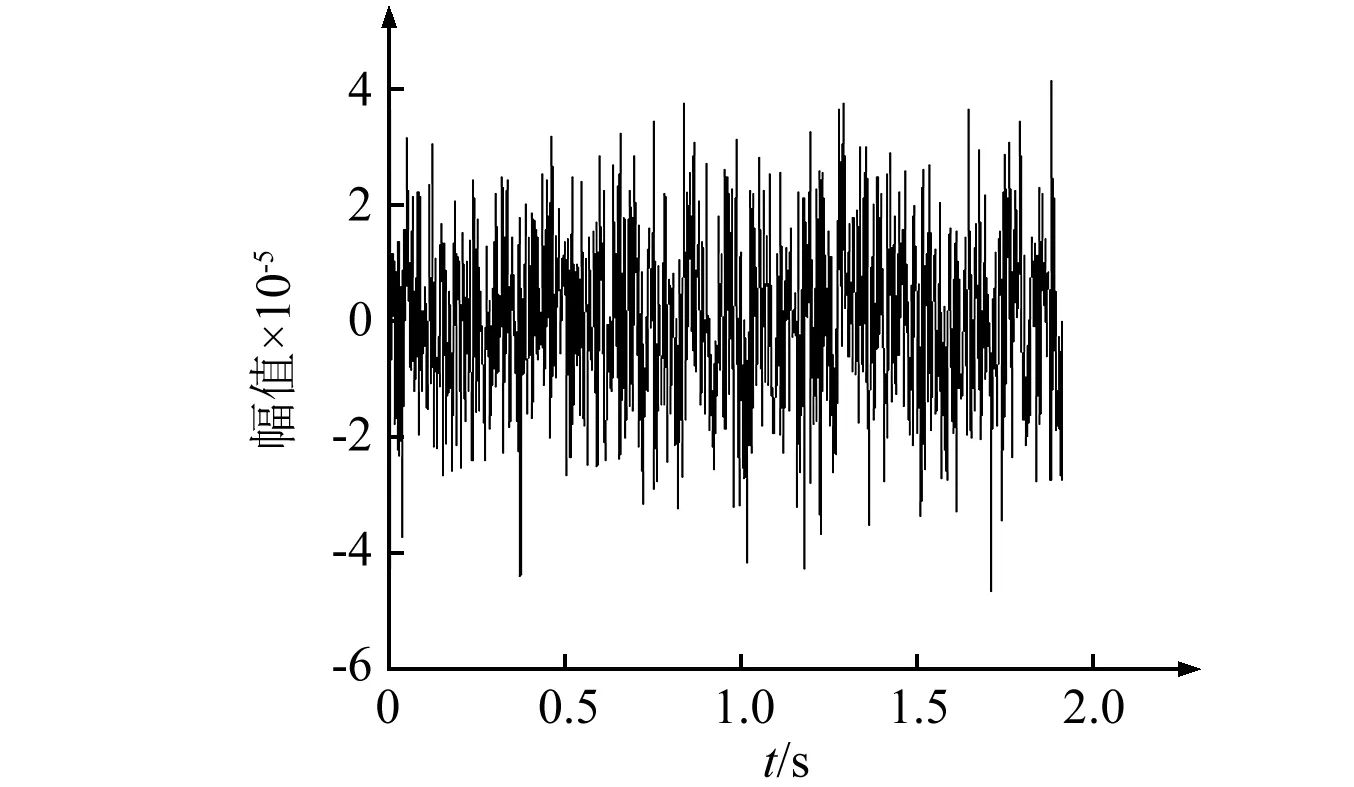
图9 不稳定点A的时域图Fig.9 Time-domain diagram of unstability point A

不稳定点A的时域图如9。

由图7可以看出，HAMM方法的计算机仿真结果和实验结果是吻合的，进一步说明HAMM方法是一种有效的预测铣削稳定性的方法。

5 结 论

针对铣削动力学模型，提出了HAMM预测铣削稳定性。通过以上研究，得到如下一些结论：

通过对局部离散误差的分析可知，HAMM的收敛速度比1st-SDM和2nd-FDM快得多。主轴转速越高，离散数少的HAMM能达到离散数较多的1st-SDM和2nd-FDM的局部离散误差，和理论分析结论一致。

无论是在单自由度还是双自由度铣削模型中，从所给的三种方法的稳定性叶瓣图中可以得出，随着离散数的增加，三种方法的计算精度都有所提高。当离散数相同时，HAMM的计算精度高于1st-SDM和2nd-FDM。特别是在双自由度铣削模型下，HAMM的计算精度远远高于1st-SDM和2nd-FDM。在离散数相同的条件下，HAMM的计算效率和2nd-FDM相当，远远高于1st-SDM。

HAMM是一种较优的预测铣削稳定性的方法，它具有较高的预测精度和较快的计算效率。实验验证表明，HAMM方法用来预测铣削稳定性是有效的。

DOI:10. 1007/s00170-016-8708-z.