基于流固耦合的立式拱顶储罐油气爆炸数值模拟

欧益宏， 李 润， 袁广强， 李国庆， 王世茂

(1. 陆军勤务学院 油料系，重庆 401311; 2. 陆军72489部队，山东 烟台 265301)

随着石油化工事业的发展，储油罐安全问题日益增多[1-3]。油罐区爆炸火灾事故时有发生，容易造成重大的伤亡。因此，为确保库区安全，需要对储罐爆炸发生发展过程以及罐体结构响应进行分析研究。

国内外许多学者针对储罐内部可燃气体爆炸发生发展规律进行了研究，在不同容积模拟储罐内部进行了实验[4-5]，对密闭空间内部着火模式[6-7]、超压荷载变化规律[8]进行了研究，同时采用不同燃烧模型[9-10]对不同容积[11]、罐顶结构[12-13]的大型储罐结构内部可燃气体爆炸进行了CFD数值模拟,得到了不同因素对储罐内部火焰形态，爆炸冲击载荷的影响。由于储罐爆炸过程及其复杂，主要包括内部油气爆炸，爆炸冲击压力波的形成与传播，冲击波与储罐结构的相互作用，目前的研究大多将壁面视为刚体，不考虑结构变形对流场发展情况的影响，事实上，储罐爆炸过程是一个典型的流固耦合过程，针对耦合条件冲击响应问题，胡可等[14-15]利用采用TNT当量模型对立式柱形容器内部蒸气云爆炸进行了数值模拟进行了研究，发现耦合效应对爆炸载荷的影响很小，在计算时可将结构视为刚体，Aune等[16-17]对薄金属板进行了冲击试验以及数值模拟研究，发现耦合条件下的结构变形更小，且更符合工程实际，在计算时不能忽略耦合效应。在进行流固耦合仿真时，研究者大多采用TNT当量模型模拟蒸气云爆炸，然而事实上，TNT爆源与可燃蒸气云具有本质上的差异，无法有效模拟整个可燃蒸气爆炸过程。因此，本文采用CFD模型对大型储罐内部爆炸进行了数值模拟，分别采用非耦合以及耦合方法对爆炸发展过程进行了计算，对两种条件下的流场以及超压荷载变化进行了对比分析，同时对耦合条件下的罐体结构响应进行了研究。以期为储罐结构抗爆抑爆优化提供一定参考。

1 数值模拟模型

1.1 控制方程

由于储罐中油气爆炸是一个具有强湍流流动性的复杂化学反应过程，因此在计算时采用RNGk-ε湍流模型来模拟爆炸过程，其中主要的控制方程为

连续性方程:

(1)

动量方程:

(2)

组分输运方程:

(3)

能量方程:

k方程:

(5)

ε方程:

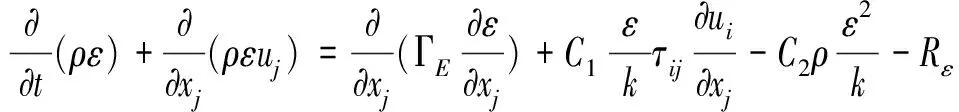
(7)

式中：ρ为密度；u为速度；P为压力；e=CvT+fsHc为比内能，E为总能量，k为湍动能，ε为湍动能耗散率；fs为第s种组分的质量分数；μt=Cμρk2/ε为湍流粘性系数；Rc为燃烧速率；Cμ取0.09；Cv为定容比热；T为温度；Hc为燃烧热，Γ*=μt/(σ)*为湍流扩散系数，(σ)*为湍流普朗特数，δij为克罗内克算子，i,j为坐标方向，C1、C2为常数，Rε为方程修正项。

1.2 燃烧模型

油气爆炸过程为强湍流燃烧过程，本文采用有限速率/涡耗散模型来对爆炸过程进行模拟，在计算过程中，为减少计算成本，并提高模型的准确程度，将油气燃烧化学反应模型简化为以下两个步骤：

反应1:

(8)

反应2:

(9)

式中：CnHm为反应物；O2为氧化剂；Fmid为中间产物，Fend为最终产物；Q1、Q2为反应释放的热量。

1.3 固体控制方程

油气爆炸超压引发结构振动、位移的控制方程为

(10)

式中：Ms为固体质量矩阵；Cs为阻尼矩阵；KS为刚度矩阵；r为固体结构位移；τs为固体结构受到的应力。

1.4 耦合面控制方程

在流体与固体的耦合面有位移、热流量、温度、应力相等，

(11)

式中:q为热流量；T为温度；下标f为流体；s为固体。

1.5 计算模型

本文分析对象采用1 000 m3拱顶储罐，具体数据由中石化设计院提供，由于储罐结构具有轴对称性，因此采用二分之一建模，计算模型分为流场与固体结构两部分，为简化模型，储罐内部爆炸强度会随着储液高度增加而降低[11]。因此，为进行保守计算，在模型简化时，假设流场内部无石油等液体以计算最大破坏效果,使其结果能用于指导实际工程应用。同时假设储罐结构除薄壳外无隔板、加强圈等其他装置，储罐结构参数，如表1所示。

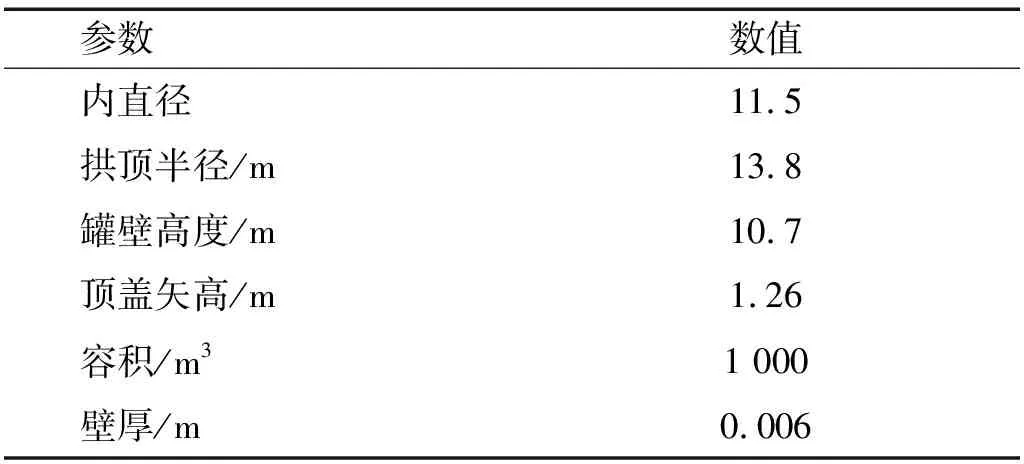
表1 储罐结构参数Tab.1 Tank structure parameters

1.5.1 流体模型

如图1，划分网格时，分别采用单元最大尺寸为0.2 m、0.15 mm、0.1 mm的网格进行了网格无关性检验,发现0.15 mm网格与0.1 mm网格计算结果相差不大，同时，考虑到动网格变形，流体内部模型最终采用单元最大尺寸为0.15 m的四面体网格进行划分，总网格数量约为46万。整个计算区域采用有限体积法对区域进行离散，压力速度耦合采用piso算法。初始区域温度设置为300 K，初始油气浓度设为1.7%(化学当量比1.05[18])压力设置为大气压，即p=0,在罐顶中心处设置压力测点PT1，罐顶-壁环向连接处设置压力测点PT2，罐底-环向连接处设置压力测点PT3，在储罐左侧壁面近底部0.8 m处设置一个半径为0.5 m的半球形区域，利用patch功能将该区域的的温度设为2 000 K，模拟人孔处着火，计算区域的边界条件设为壁面封闭、绝热、无渗透。

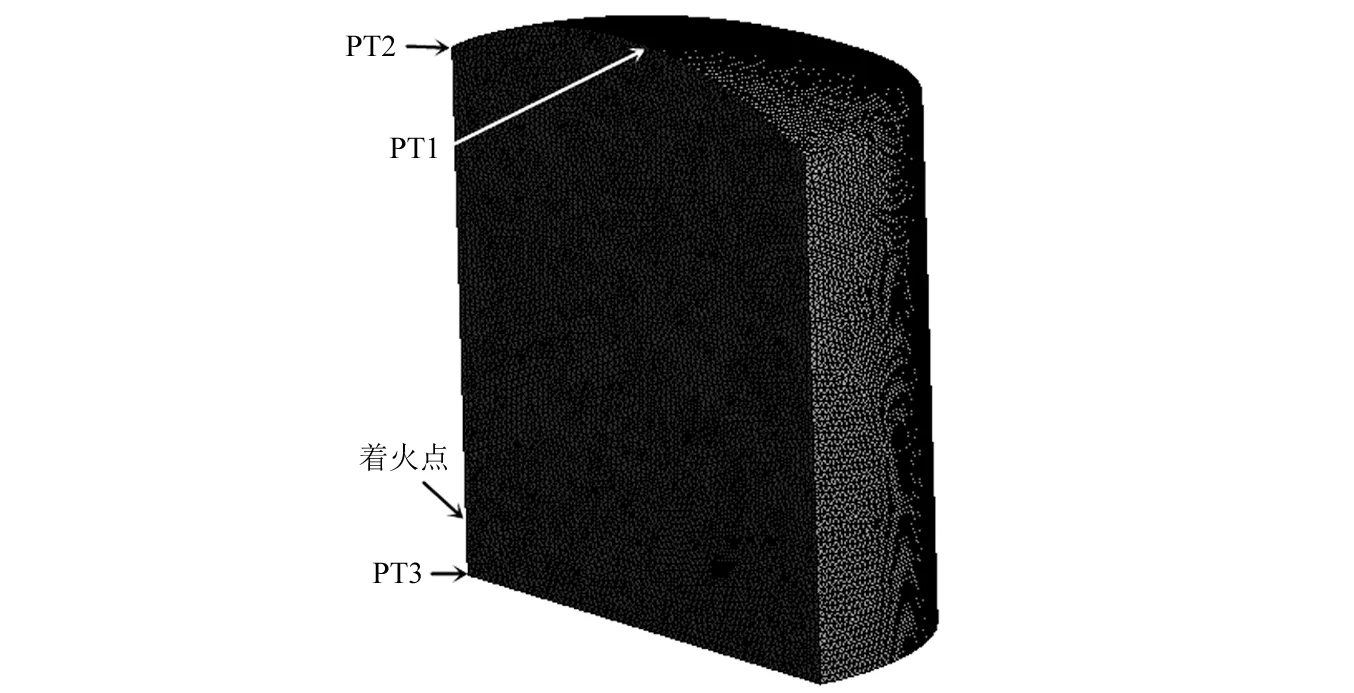
图1 流体区域网格Fig.1 Fluid area grid

1.5.2固体模型

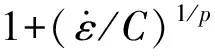
(12)

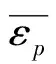
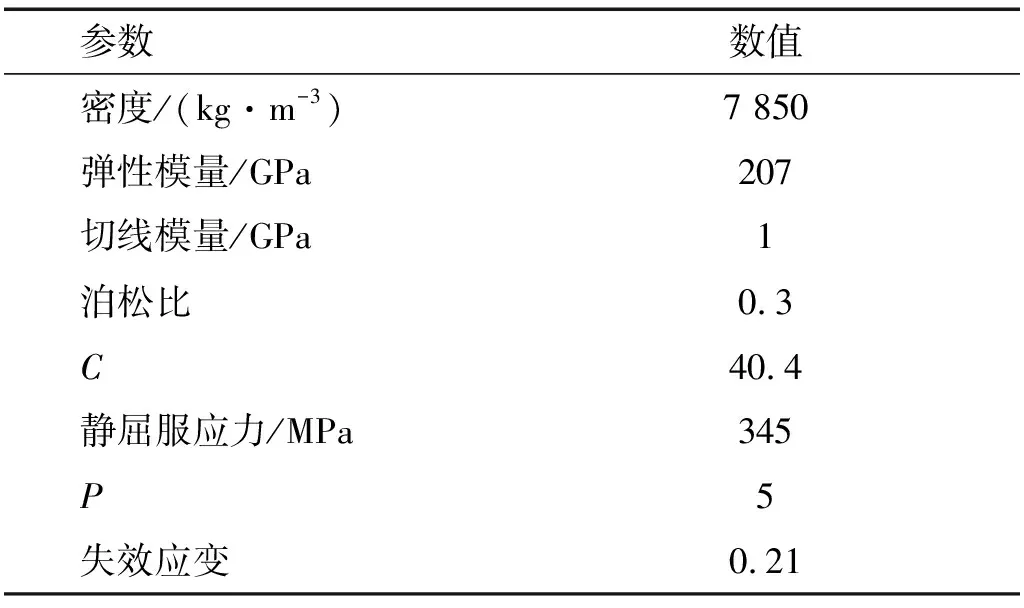
表2 模型材料参数Tab.2 Model material parameters

图2 固体域网格Fig.2 Solid domain grid

1.6 耦合参数及动网格设置

建立储罐爆炸双向耦合模型需要分别在流体域与固体域设置耦合面，在本文模型中，由于考虑的是储罐内部起爆，因此考虑将储油罐罐顶以及环向壁面以及相对应的流场面设为流固耦合面，由于计算流场边界存在变形问题，因此采用动网格模型中的弹簧光顺以及网格重构法对流场边界进行更新，弹簧光顺的思路为将网格节点之间的连线近似为弹簧，通过计算节点力的平衡方程得到各节点光顺后的位置。方程为

(13)

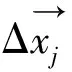
然而，只使用弹簧光顺法时，当边界位移远大于局部网格尺寸时，网格质量会下降甚至出现负体积网格，为了解决此问题，本文采用网格重构法将这些超出网格尺寸标准的网格收集起来，并在该网格基础上进行局部网格重构并重新对其进行质量评估。

流场计算采用fluent软件，结构计算采用 transientstructure模块进行计算，流固数据交互在workbench中的systemcoupling模块进行。在数据交互过程中，对位移采用界面保形插值法进行传输，对压力采用守恒插值进行传输[20]。

1.7 模型验证

为验证CFD模型的有效性，本文对已开展的模拟储罐油气爆炸试验进行了数值模拟并进行了对比，图3为模拟储罐实验台架，储罐底部半径为0.5 m,全高为0.8 m,储罐容积为625 L,其中P1、P2、P3为压力传感器设置位置，P1置于罐顶中部，P2置于罐体壁面中部距罐底0.4 m,P3置于罐底中部，点火点置于人孔附近，距罐底0.1 m。具体实验细节可以参考文献[8],图4为不同测点实验与仿真的超压变化对比图，可以看到，模拟储罐油气爆炸数值模拟与实验的超压上升以及振荡趋势基本一致，但是由于数值模拟中将壁面设为绝热条件，在罐内油气完全燃烧后没有热量散失，因此超压一直保持稳定不变，在实际实验中，由于储罐壁面的热耗散，导致超压在达到超压峰值以后会逐渐减弱。

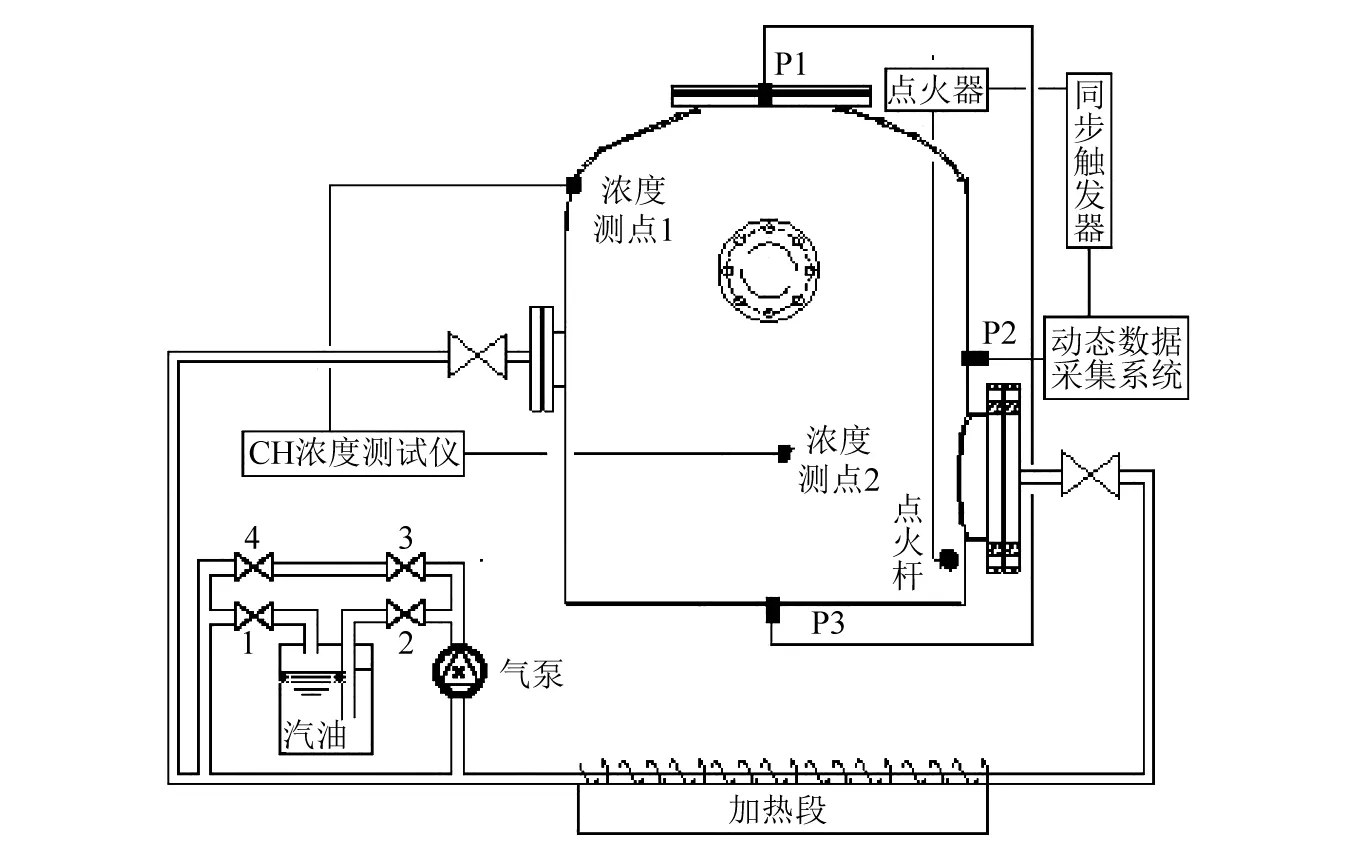
图3 模拟储罐台架Fig.3 Simulation tank bench

总的来说，该CFD模型能够较为准确的模拟罐内油气爆炸过程，因此可将其应用于实际的立式拱顶油罐油气爆炸中。

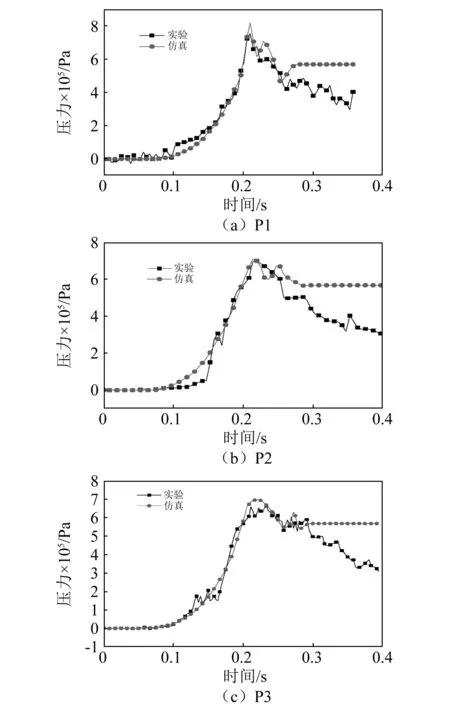
图4 实验与仿真超压时序图Fig.4 Experimental and simulation overvoltage timing diagram

2 结果分析与讨论

2.1 耦合结果分析

2.1.1火焰发展

图5为非耦合(即将罐壁示为刚体)以及耦合条件下储罐内部爆炸的火焰发展情况，可以看到，从整体上来看，两种条件下火焰发展模式基本相同，着火起爆后，火焰以层流速度缓慢发展，由于着火位置位于容器壁面靠近底部的位置，因此火焰以半球型向四周传播，此时，由于火焰面积较小，单位时间内参与反应的未燃油气较少，火焰结构发展平稳，随着储罐内部反应的进行，火焰逐步湍流化，火焰锋面面积逐渐增大，随着火焰与罐壁的逐渐接触，由于罐壁面的局部扰动导致火焰湍流化加剧，火焰反应进一步加剧，随着储罐内部反应的进行，火焰逐步蔓延至整个储罐内部。

图5 火焰发展情况Fig.5 Flame development

图6为火焰传播速度时序图，火焰传播速度采用文献[21]的计算方法，结合不同时间点火焰结构进行对比可以看到，经过前期短暂的层流火焰燃烧后，在无约束状态下，火焰传播速度在压力波与火焰的耦合激励下迅速上升，并于300 ms时达到峰值65.05 m/s,随后，火焰右侧壁面开始干扰火焰及压力波的传播，在反射波的影响下，火焰传播速度开始下降，随着燃烧的逐步进行，储罐内部超压逐渐升高，从耦合条件下储罐壁面发生变形，内部流场边界发生变化，导致其火焰发展速度比非耦合条件下的火焰发展速度稍慢，可以看到，非耦合条件下，720 ms时储罐内部已经燃烧完全，而耦合条件下780 ms时才完全燃烧。

图6 耦合与非耦合条件下火焰传播速度时序图Fig.6 Coupling and non-coupled flame propagation velocity under the timing diagram

2.1.2超压趋势

图7为非耦合以及耦合条件下超压时序图，为进行分析，分别取罐顶中心处PT1,罐顶-壁环向连接处PT2，罐底-环向连接处PT3三个测点的超压时程图进行对比，可以看到，储罐内部不同测点超压趋势基本相同，均呈现出缓慢增长-急剧上升-压力振荡-稳定不变的变化趋势，结合图5可以看出，由于储罐内部初期处于层流燃烧状态，燃烧区域较小，因此超压速度上升较为缓慢，随着燃烧的进行，火焰面积逐渐变大，已燃气体受热膨胀，火焰锋面前未燃气体被压缩，形成前驱压力波，由于火焰前驱压力波的传播，导致波前大量未燃气体被预热，形成高温高压的未燃气体区域，当火焰传播至该区域时，未燃气体被迅速引燃，燃烧进一步加剧，导致超压急剧上升并到达第一个超压峰值，在到达第一个超压峰值后，由于压力波在火焰前峰与壁面间往复碰撞，反射，因而形成了超压振荡现象，随着储罐内部可燃气体燃烧完全，罐内不再产生热量，由于在计算时将壁面设为绝热条件，因此罐内超压逐渐保持不变。

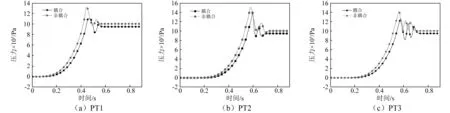
图7 非耦合以及耦合条件下超压时序图Fig.7 Overcurrent timing diagram for uncoupled and coupled conditions

将不同条件下超压关键参数对比分析如表3所示，将不同测点进行对比，可以看到，相比罐顶中心点PT1，环向连接处测点PT2、PT3由于压力波的反射以及反射波的折向传播更为剧烈，因此超压峰值更大,反之升压速率方面，由于PT1达到最大超压峰值的时间更短，因此升压速率更快，为2.92 MPa/s。在石油化工行业中，储罐若先从底部破坏会造成巨大财产损失以及次生灾害的发生，因此，PT2与PT3超压参数对比是实际工程中关心的重点，可以看到顶壁连接处超压峰值最大，为Pmax=1.51 MPa，但底壁连接处振荡脉动更为剧烈。

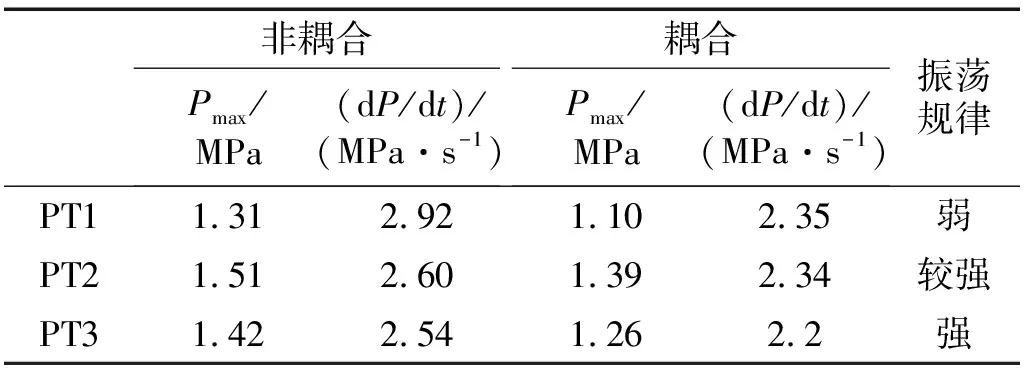
表3 超压关键参数对比Tab.3 Overpressure key parameters comparison

对比耦合与非耦合条件下各项超压参数，可以看到，耦合条件下超压峰值平均比非耦合条件下小10%左右，同时耦合条件下振荡脉动较小，说明耦合效应能减小脉冲速度以及爆炸载荷。该结论在Aune[16-17]的研究中得到了证实。

2.1.3 耦合效应分析

为深入分析耦合效应对火焰传播以及爆炸载荷的削弱原因，本文绘制了流场矢量迹线图并进行了对比，可以看到，一方面，耦合效应导致储罐变形，罐内流场空间增大，未燃气体被稀释，未燃气体分子与氧分子碰撞反应机率降低，参与反应的活化分子数量减少，燃烧反应速率变慢，进而导致传播速度变慢，燃烧速率的减慢也会导致升压速率的减缓。同时，相对非耦合条件，耦合条件下储罐内部体积的增大也使得已燃气体对未燃气体的压缩效应减弱，导致压力波的传播速度减慢。另一方面，耦合效应下，流场壁面变得更加圆滑，这对流场以及压力波都有较大影响，由于非耦合下的壁面边界更为尖锐，因此其对于内部流场的干扰影响更为激烈，结合流场图，可以看到在500 ms时，非耦合条件下，流场内部右上角，左下角已经形成涡旋结构，火焰锋面湍流效应较为明显，而此时，耦合条件下反应区内尚无明显的涡旋结构形成，已燃区域涡旋结构的形成会对内部流场形成强烈的扰动，进而引发火焰锋面失稳导致湍流火焰加速，导致超压峰值以及振荡脉动进一步提升。

图8 非耦合与耦合条件流场矢量迹线图Fig.8 Uncoupled and coupled flow field vector trace

2.2 储罐结构响应分析

相比非耦合条件，耦合条件分析还能得到储罐结构响应情况，图9为储罐结构变形图(0.5倍变形显示)，结合储罐顶部/壁面最大位移时程曲线可以看到，储罐变形可以分为无明显变形-顶部拱起-壁面膨胀-变形减缓四个阶段，结合图5可以看出，储罐内部着火爆炸初期，由于燃烧较为缓慢，爆炸产生的超压较小，因此储罐各处基本上无变形，随着燃烧的逐渐进行，超压逐渐上升，储罐拱顶和壁面先后出现膨胀变形，400 ms时顶-壁连接处由于拱顶与壁面的膨胀变形出现而拉伸并出现褶皱变形，由图10可以看到，储罐不同区域变形时程曲线均显现出平稳不变-急剧增长-缓慢变化的区域，由于储罐环向壁面较罐顶具有较好抗爆性能，因此罐顶较环向壁面变形发生更快，400 ms时顶部最大变形(0.834 m)为罐壁最大变形(0.472 m)的1.77倍，750 ms时材料变形开始减缓，但顶部最大变形(2.57 m)仍为环向壁面(2.36 m)的1.09倍，因此储罐顶部较壁面更易被破坏。

图9 结构变形图Fig.9 Structural deformation diagram

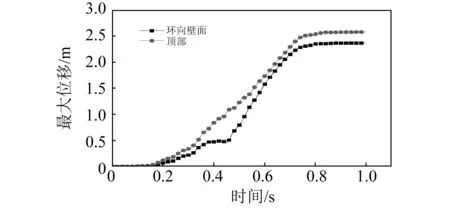
图10 顶部及环向壁面最大位移时程图Fig.10 Top and ring wall maximum displacement time history

图11为储罐von Mises等效应力云图分布情况，可以看到，爆炸初期，由于只有着火点附近有压力变化，因此最大等效应力首先出现于着火点处，随后，最大等效应力出现于罐壁-罐顶连接处并逐渐增大，出现该现象的原因一方面是因为该区域超压峰值由于压力波的反射、汇聚比其他区域更大，另一方面是由于顶部与环向区域的变形会对该位置产生较大的拉应力，400 ms时连接处最大应力为388 MPa,已超过材料的静屈服应力345 MPa，材料已进入塑型区域，极易被破坏，随着超压的急剧上升，罐顶、储罐环向壁面变形加剧，罐顶中心、罐壁环向区域等效应力均超过了材料的屈服极限，说明此时该区域极易被破坏。800 ms时，最大应力区域出现于顶-壁连接处以及底-壁连接处附近，在实际工程中，由于储罐拱顶一般会加肋，罐壁环向会增设抗风圈以及加强圈。结合2.1.2所得结论，需要对顶-壁连接处进行弱化连接处理，使得爆炸时该处出现断裂破坏进而产生泄压，同时对底部进行加强，以防止油罐爆炸灾害所导致的罐底开裂的重大事故发生。

图11 储罐爆炸应力云图Fig.11 Tank explosion stress diagram

3 结 论

本文对1 000 m3拱顶储罐结构内部油气爆炸过程进行了数值模拟并进行了模型实验验证，对耦合与非耦合条件下的爆炸的流场、超压变化数据进行了对比分析，同时，对耦合条件下储罐结构动力响应进行了分析。得到以下结论：

(1)非耦合条件与耦合条件下火焰结构变化趋势基本相同，但由于耦合条件下储罐壁面发生变形，因此耦合条件下的火焰传播速度稍慢。耦合条件下储罐内部完全燃烧时间比非耦合条件下慢60 ms。

(2)非耦合与耦合条件下各位置的超压变化趋势基本相同，均呈现出缓慢增长-急剧上升-压力振荡-稳定不变的趋势，其中非耦合条件下罐顶-壁连接处超压峰值最大,为1.51 MPa，但耦合条件较非耦合条件超压峰值低10%左右，且脉动较小，说明耦合效应能减小爆炸载荷10%左右以及部分振荡脉动。

(3)爆炸时，储罐顶部变形最大，最大应力区域出现在顶-壁，底-壁连接处，考虑到实际工程情况，需要对顶-壁连接处进行弱化连接处理，使得爆炸时该处出现断裂破坏进而产生泄压，同时对底部进行加强，以防止油罐爆炸灾害所导致的罐底开裂的重大事故发生。