RCS对舵面控制特性影响的数值模拟

陈琦，陈坚强，张毅锋，袁先旭

中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000

可重复使用运载器(Reusable Launch Vehicle,RLV)再入飞行具有飞行范围广、飞行特性变化剧烈和操纵复杂等特点。再入返回初期，由于空气稀薄、来流动压较低，导致气动舵面效率降低甚至失效，必须采用反作用控制系统(RCS)进行姿态控制和轨迹追踪；随着飞行高度降低，来流动压增加，RCS效率降低，气动舵面逐渐介入操纵，在此过程中，RCS和气动舵面一起对飞行器进行控制，通过RCS/舵面复合控制技术，可以大幅降低RCS流量、节省燃料；最终，RCS退出操纵，气动舵面独立控制飞行器的飞行姿态[1-3]。

RLV在采用RCS/舵面复合控制技术进行飞行姿态控制时，气动舵面与RCS之间可能存在相互干扰，影响彼此的控制效果。在气动控制面与喷流相互干扰的研究方面，国外文献多集中在飞机襟翼与发动机喷流之间的相互干扰效应[4-8]，尚未见RCS/气动控制面干扰的研究报道。国内对喷流干扰的影响研究多集中在RCS与自由来流主流之间的干扰效应[9-15]，陈坚强等[16]采用数值模拟手段研究了侧向喷流及与舵面运动之间的相互干扰，分析了舵面运动过程对喷流控制效果的影响。总体来看，对气动舵面与RCS相互干扰的影响研究，目前国内外相关工作较少，相互影响的机理和严重程度尚不明晰，从而给RCS/舵面复合控制系统的设计带来较大压力。

本文针对可重复使用运载器的RCS/舵面干扰问题，结合动网格技术，采用数值模拟研究喷流开启或关闭时飞行器运动对不同舵面操纵方式的动态响应过程，舵面的操纵方式包括突发短暂干扰、突发持续干扰以及连续快速摆动等。本项研究可为RCS/舵面复合控制系统设计时，考虑对RCS/舵面相互干扰的补偿提供参考。

1 问题描述

可重复使用运载器(图1)的外形主要由机身、方向升降舵(又称V形立尾)、襟副翼、体襟翼等组成，控制系统则由以上各种气动控制面、RCS以及轨道机动系统(OMS)组成。

从气动控制面的命名规则可看到，方向升降舵提供俯仰和偏航控制，襟副翼控制滚转并调节阻力，体襟翼则主要用于俯仰方向的配平[16]。以俯仰方向为例，再入返回初期，主要采用RCS进行姿态控制；随着来流动压增高，气动控制面开始产生控制力矩，此时采用RCS、方向升降舵、襟副翼以及体襟翼组合的方式进行俯仰方向配平及控制；动压进一步增大后，RCS逐渐退出，襟副翼主要用于调节阻力，此时只需方向升降舵和体襟翼即可提供足够的俯仰控制力矩[17]。

从可重复使用运载器外形可以看到，以侧向喷流为例，喷口位置距离方向升降舵、襟副翼和体襟翼均较近，喷流开启或关闭时，势必会产生RCS/舵面干扰，影响彼此的控制效果。对超声速来流问题，襟副翼处于喷口上游，其偏转会直接影响喷流的控制效果[16]；而喷口的位置又处于升降舵和体襟翼的上游，喷流开启或关闭将对飞行器的俯仰配平特性产生重要影响。本着从简单到复杂的研究原则，首先从襟副翼与侧向喷流的干扰问题入手，研究喷流开启和关闭时，飞行器俯仰运动对襟副翼偏转的动态响应过程。为叙述简单，后文一般直接称襟副翼为舵面，襟副翼的偏转角简称为舵偏角。

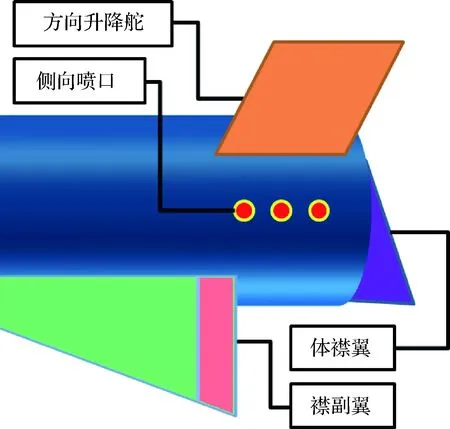
图1 气动控制面和反作用控制系统相对位置示意图Fig.1 Sketch of relative positive of aerodynamic control surfaces and RCS

2 数值方法

采用数值模拟方法研究可重复使用运载器的RCS/舵面干扰问题。

飞行器的非定常绕流流场通过求解Navier-Stokes方程获得。空间离散格式采用原始变量NND(None oscillation， None free parameter，Dissipative difference scheme)格式，限制器选用minmod限制器；非定常时间推进采用Jameson双时间步方法，以上方法的具体描述可参考文献[18]。

描述飞行器运动的刚体动力学方程和运动学方程(两个方程通常也直接称为RBD (Rigid Body Dynamics)方程)采用四阶Runge-Kutta方法进行求解。

飞行器的运动流场需要耦合求解Navier-Stokes方程和RBD方程来获得，这里采用松耦合的求解方式[18]，即Navier-Stokes方程和RBD方程分别独立求解，在时间域上交错推进，最终获得飞行器的运动流场。

对于舵面的偏转问题，由于涉及襟副翼和飞行器本体之间的相对运动，需要采用动网格技术进行处理，这里采用局部网格动态变形技术[19]。其过程可简述如下：首先，在生成网格时，襟副翼附近的网格由一块或若干块网格组成，将襟副翼封闭包裹，这些块统称为一个“超块”；其次，记录“超块”内每个网格点相对物面和“超块”边界的位置关系；再次，在舵面运动过程中，物面网格点的更新根据绕定轴的旋转方程直接得到，而“超块”的外边界与飞行器本体网格块之间是对接关系，在舵面运动过程中保持不变；最后，根据更新后的“内边界”和“外边界”点，以及网格点的位置关系，基于弹簧弹性变形原理，更新“超块”内部的网格点。

图2给出了采用局部网格动态变形技术将舵面偏转±10°后的网格。计算过程中，每个时间步迭代结束后，都需要依据舵面的位置自动更新舵面附近的空间网格点。在网格变形过程中，为避免网格运动给数值解引入额外的数值误差，需要满足几何守恒律条件。

图2 舵面偏转±10°的网格Fig.2 Grid at ±10° deflection angles

对喷流的模拟通过给定喷流边界的方式进行，即根据喷管的入口参数和喷管形状，通过数值模拟喷管内部流动得到喷管出口处的压力、密度和速度分布等参数[16]，这些参数共同构成喷流边界。在数值模拟时，若喷流开启，则直接将这些参数赋值到对应的网格点上；若喷流关闭，喷口退化为固壁边界[18]，速度满足无滑移条件，温度由等温壁给定。在研究侧向喷流与襟副翼的干扰效应时，侧边5个喷口中的3个处于开启状态，其他两个喷口指定为固壁边界(见图2)。图3给出了喷流完全开启时喷口表面的压力和马赫数分布云图，其中红色代表最大值，蓝色代表最小值。3个喷口的流动参数分布完全相同，不考虑背压对喷管性能的影响。在数值计算时，喷流突然开启时，喷口附近流动参数梯度较大，给数值计算带来困难。这里指定在10个时间步内喷流达到完全开启状态，中间过程采用线性插值方式实现。

综合以上方法不难看出，研究RCS/舵面干扰问题，涉及到气动/运动耦合求解、动网格以及喷流模拟等多项技术，求解难度较大，这也是此类研究较少开展的原因之一。

图3 喷管出口处的压力和马赫数分布云图 Fig.3 Distribution contours of pressure and Mach number at jet nozzle

3 侧向喷流对俯仰配平特性的影响

在开始研究RCS/舵面干扰的动态特性之前，首先分析定态情况下侧向喷流对俯仰配平特性的影响，作为后续研究的基础。来流计算条件均给定为马赫数Ma=3，高度H=30 km，计算攻角α视研究问题给定，无侧滑角。需要说明的是，侧向喷流开启后，会引入附加的偏航和滚转力矩，但本文未考虑对偏航和滚转运动的影响，即偏航和滚转方向是强制固定的，只考虑对俯仰方向的影响。

图4是喷流开启和关闭时，俯仰力矩系数Cm随攻角的变化曲线。可以看到，喷流开启和关闭对俯仰力矩有较大影响,喷流开启时飞行器的配平攻角为-1.04°,而喷流关闭时飞行器的配平攻角约为0°，配平攻角相差1.04°。

为研究喷流开启和关闭对俯仰配平特性影响的原因，图5给出了喷口附近的压力云图比较。在喷流开启或关闭时，襟副翼表面的压力分布几乎没有变化，不会直接影响襟副翼的控制和配平效率；但飞行器的方向升降舵却刚好处于喷流的影响区，喷流开启时，在喷流前方形成的弓形激波刚好打到方向升降舵的迎风面，形成高压区，产生低头力矩，导致喷流开启时飞行器的配平攻角比喷流关闭时的配平攻角要低1.04°。

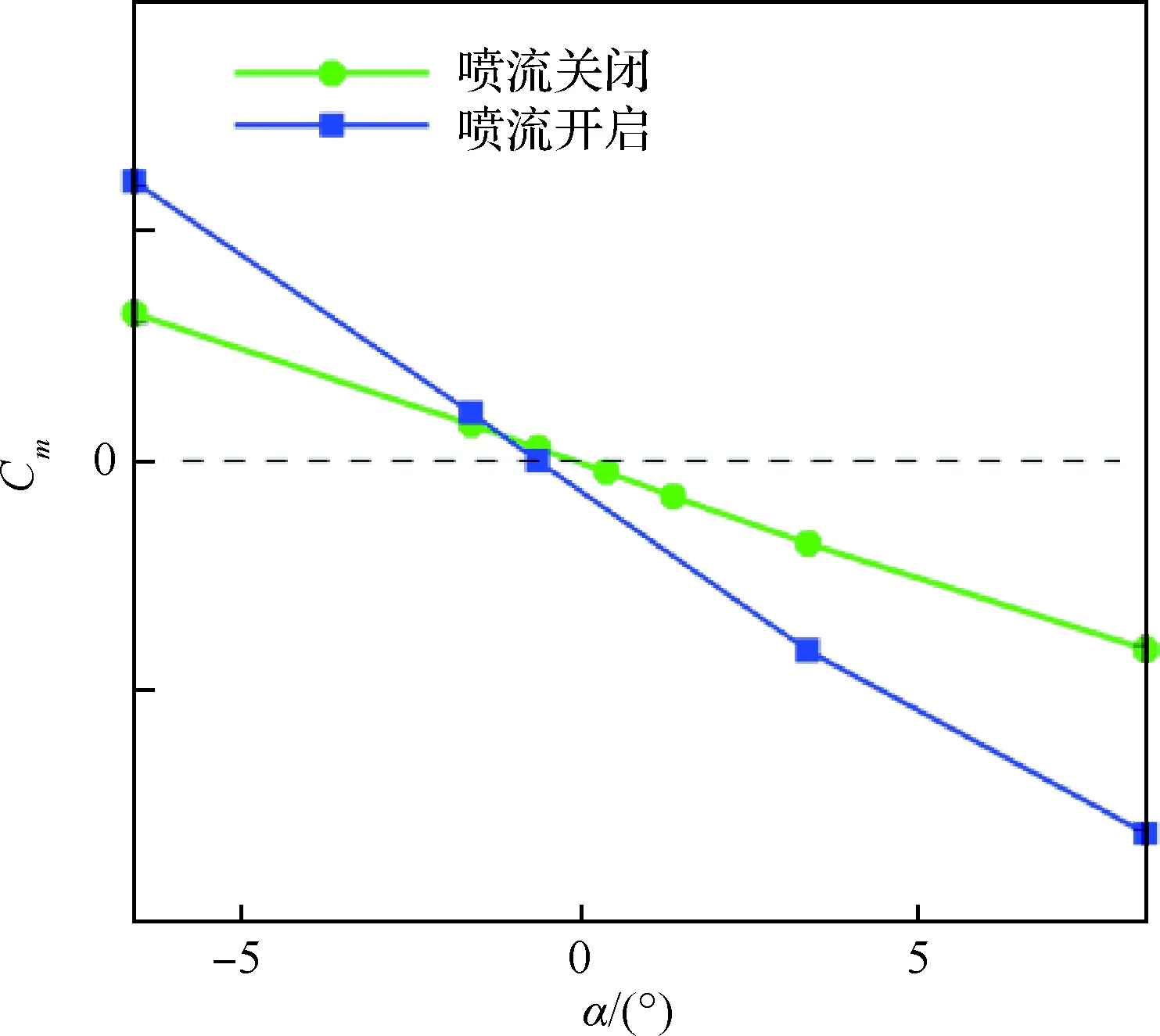
图4 俯仰力矩随攻角变化曲线的比较 Fig.4 Comparison of variation curves of pitching moment with angles of attack

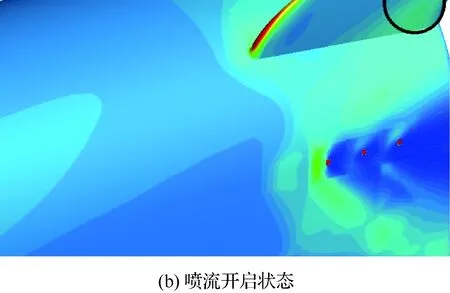
图5 喷口附近压力分布云图比较Fig.5 Comparison of contour distributions of pressure around jet nozzles

4 侧向喷流对舵面控制特性的影响

第3节分析了定态情况下侧向喷流对俯仰配平特性的影响，本节将在此基础上着重开展侧向喷流与襟副翼的动态干扰问题研究，分析喷流开启和关闭时，飞行器对襟副翼偏转的动态响应过程。

襟副翼的偏转模式分3种：突发干扰模式、持续干扰模式和连续周期摆动模式。3种偏转模式对应的舵面运动函数分别为

(1)

(2)

δ=δ0+δmsin(2πt/T)

(3)

式中：δ0和δm分别为初始舵偏角和舵偏幅值，在文中取值为δ0=0°，δm=5°；t为时间;T为摆动周期，对式(1)和式(2)，T=0.1 s，对式(3)，T=0.1～3.0 s。图6是3种偏转模式下，襟副翼的偏转角随时间的变化历程(T=0.1 s)。

图6 3种偏转模式下舵偏角随时间的历程Fig.6 Time history of deflection angles at three different deflection modes

4.1 突发干扰模式

图7 飞行器对襟副翼短暂干扰的动态响应Fig.7 Dynamic response of vehicle under temporary disturbance mode

4.2 持续干扰模式

图8和图9是舵面持续干扰模式下，飞行器对扰动响应的模拟结果。图8对应舵面向下偏转情况(对应式(2)中的δm=5°)，飞行器受低头力矩作用，振荡收敛到新的配平位置。喷流关闭时，新的配平攻角为-3.07°；喷流开启时，新的配平攻角为-4.39°，配平位置相差约1.32°，比舵面未偏转时的差别量1.04°略大。在相同的舵面操纵下，喷流关闭时，飞行器攻角变化为-3.07°(从初始配平位置0°到新的配平位置-3.07°)；喷流开启时，飞行器攻角变化为-3.35°(从初始配平位置-1.04°到新的配平位置-4.39°)。很明显，该状态下，相对于喷流关闭状态，喷流开启将增强襟副翼对俯仰方向的控制效果。

图9则是舵面向上偏转时(对应式(2)中的δm=-5°)，喷流开启或关闭时对控制效果的影响。在相同的舵偏角作用下，喷流关闭时，新的配平攻角为3.05°；喷流开启时，新的配平攻角为2.09°，配平位置相差约0.96°，比舵面未偏转时的差别量1.04°略小。喷流关闭时，飞行器攻角变化为-3.05°(从初始配平位置0°到新的配平位置3.05°)；喷流开启时，飞行器攻角变化为-3.13°(从初始配平位置-1.04°到新的配平位置2.09°)。相对于喷流关闭状态，喷流开启也增强了襟副翼对俯仰方向的控制效果，但增强的效果相对舵面向上偏转时有所减弱。

图8 飞行器对襟副翼持续干扰的动态响应(δm=5°)Fig.8 Dynamic response of vehicle under continuous disturbance mode (δm=5°)

图9 飞行器对襟副翼持续干扰的动态响应(δm=-5°)Fig.9 Dynamic response of vehicle under continuous disturbance mode (δm=-5°)

综合以上模拟结果，对可重复使用运载器外形，由于喷流前方的弓形激波会打到方向升降舵上，形成高压区，导致喷流开启时的配平攻角比关闭时要低约1.04°。在正向舵偏的操纵作用下，喷流开启对舵面控制效果的增益明显，攻角改变量相差约9.12%(舵偏角5°)。这主要是由于正向舵偏产生低头力矩，而随着飞行器作低头运动，弓形激波打到方向升降舵上的区域增大，也即高压区增大，相当于增强了襟副翼对俯仰方向的控制效果。在负向舵偏的操纵下，喷流开启对控制效果的增益减弱，主要是由于负向舵偏产生抬头力矩，而随着飞行器攻角增大，弓形激波打到方向升降舵上的区域向后移动，作用区域减小，对襟副翼在俯仰方向控制效果的影响也减弱；可以预测，随着攻角进一步增大，方向升降舵有可能处于喷流流场的影响区域之外，此时喷流的开启或关闭对俯仰控制效果几乎不存在影响。

4.3 连续周期摆动模式

飞行器俯仰运动对襟副翼周期性摆动的响应特性与其自身的固有振动频率密切相关，固有振动频率可以通过数值模拟飞行器的自由振荡过程获得，根据图7～图9中攻角随时间的变化曲线，可以得到飞行器的俯仰固有振动周期约为3.6 s。

首先考虑喷流关闭的情况，数值模拟的起始攻角为-0.1°(配平点附近)，图10是不同摆动周期时攻角对舵偏角响应的相图。为使结果更清晰，图10中未画出起始的响应过程，只保留了稳定后的模拟结果。可以看到，在舵偏频率f由小到大的变化过程中，飞行器俯仰振动的振幅经历了由小到大再变小的过程，最大响应振幅发生在舵偏频率接近飞行器固有频率时。同时，迟滞圈的斜率也经历了由负到正的变化过程，转折点同样发生在舵偏频率接近飞行器固有频率时。由于正的舵偏角对应负的配平攻角，在相位滞后不太严重的情况下，其迟滞圈的斜率必然为负，迟滞圈的斜率发生反转，表明相位滞后角已经超过90°。

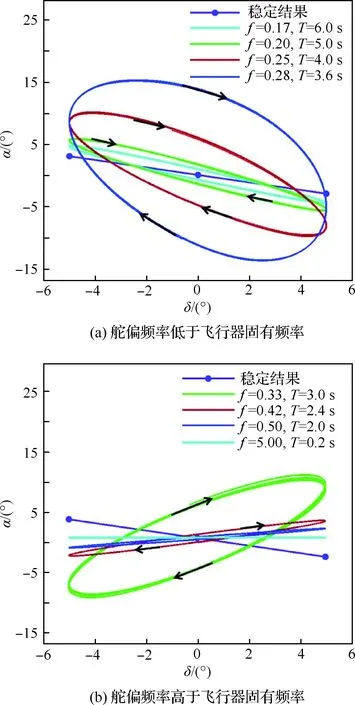
图10 攻角-舵偏角相图(喷流关闭)Fig.10 Phase diagram of angles of attack to deflection angles angles (jet off)

图11是相位滞后角随舵偏摆动频率的变化曲线，fn为飞行器固有振动频率。当舵面摆动频率超出飞行器固有振动频率后，滞后相位角φ的值将迅速增加，飞行器的响应会出现严重的滞后现象。

图12比较了喷流开启和关闭时，飞行器俯仰运动对舵面周期性摆动的响应过程，摆动频率选在固有振动频率fn两侧。从模拟结果可以看到，在舵面摆动频率小于飞行器固有振动频率时，两种状态下两条曲线并非完全“平行”，表明喷流开启时除了影响配平点外，RCS和舵面之间还存在非线性干扰效应；但当舵面摆动频率大于飞行器固有振动频率后，喷流开启后攻角的响应曲线与关闭时相比，平移了-1.04°，此时RCS和舵面之间的非线性干扰效应基本被“抹平”。

图11 滞后的相位角随频率变化曲线(喷流关闭) Fig.11 Curve of variation of phase angle with frequency (jet off)

图12 喷流开启和关闭时攻角的响应比较Fig.12 Comparison of responses of angles of attack at jet on and off

5 结 论

1) 对可重复使用运载器外形，在计算状态下，由于侧向喷流与方向升降舵之间的干扰效应，导致喷流开启时飞行器的配平攻角比喷流关闭时低1.04°。

2) 随着攻角增大，RCS开启会增强襟副翼对俯仰方向的配平效果；而随着攻角减小，增益的效果减弱甚至消失。

3) RCS襟副翼之间的干扰呈现一定的非线性、非定常效应，但量值不大。从研究情况来看，RCS开启或关闭主要影响方向升降舵表面的压力分布，预计RCS与方向升降舵之间的干扰效应更强，下一步将针对此问题展开研究。