用于薄片试样弹塑性应力-应变分析的半解析方法

刘勤，蔡力勋，陈辉

西南交通大学 力学与工程学院，成都 610031

在航空、核电、微机械等关键工程领域中，结构零部件经受温度、压力等单向或循环载荷作用，材料的单调与循环力学性能对于材料与结构的安全评价具有重要意义[1-2]。新材料研制、结构小型化会因材料尺寸限制，采用传统大尺寸试样的试验方法难以满足材料性能测试的需求[3-4]。开展以毫米厚度薄片小试样获取材料的力学性能测试方法创新研究有重要意义。

通过小试样获取材料的力学性能已有不少研究。对于传统构型的小试样常用单轴拉伸试验获取材料性能，其中Liu等[5]研究尺寸效应对焊接材料的影响，完成了不同厚度的等直片状试样单轴拉伸试验，并用数字图像相关(Digital Image Correlation,DIC)技术测量获取载荷与局部应变关系；Gussev[6]和Liu[7]等考虑到辐照装置的体积制约和样品放射性的严格限制，设计了厚度为0.2 mm、长度为2 mm的“狗骨型”试样，获取核反应堆材料的单调应力-应变关系。而对于非常规构型小试样，常省去试样夹持段，通过压缩或者压入的方式加载，其中Nemat-Alla[8]、Reddy和Reid[9]为研究圆管材料的轴向或环向的力学性能，分别采用轴压或侧压管试样的方法获取材料两个方向应力-应变关系；为得到在役核电材料力学性能，Manahan等[10]提出了小冲杆的试验方法平压小圆片试样；Cheng[11]通过刚性压头压入被测材料实现了材料单轴本构关系的获取。但这些压力加载的方法通常依赖于有限元回归，难于能给出较为简单的解析描述。循环应力幅-应变幅曲线是表示循环变形下材料变形抗力的重要特性，定义为循环变形达到稳定状态时，连接各应变幅下应力-应变滞回曲线顶端的曲线。传统试验方案采用标准试样[12]在多级应变幅下的轴向等幅对称循环试验获取。为研究铝薄膜和铜薄膜的疲劳性能，Read[13-14]等设计完成了“哑铃”状薄片试样的拉-拉疲劳试验，该试验方案能较好地测试在受拉的柔性构件力学性能，但并不能通过该试样获取材料对称低循环应力-应变关系。Melander等[15-17]设计了厚度为1.4 mm、长宽比小于2的等直板试样完成轴向应变控制的拉压循环试验，试验的应变幅限制在0.25%内以避免失稳，因而未获得较大应变范围的循环应力-应变关系。既为了防止薄板试样失稳又保证足够的应变幅范围，Martin[18]和Wisner等[19]采用圆弧漏斗试样开展对称循环试验，分别利用厚度方向与宽度方向的应变进行循环控制，以漏斗最小横截面的平均弹性应变幅与修正的等效塑性应变幅之和作为轴向应变幅，并以该截面的平均应力作为轴向应力幅，建立材料的循环应力幅-应变幅关系。贾琦等[20-21]针对具有循环Masing效应的特定材料，提出了取等直圆棒试样最大应变幅稳定阶段应力-应变滞回环上升段作为材料的循环本构关系，但未给出通过漏斗薄片试样来获取材料的循环本构关系的方法。尹涛等[22-23]完成了毫米厚的漏斗薄片试样的低周疲劳试验设计，通过建立能量分离函数原创地提出了预测循环应力幅-应变幅关系的半解析方程，该方法所采用的方程较为复杂，局限于具有几何相似性的漏斗薄片试样。

本文作者[24-27]提出了Chen-Cai能量等效方法，给出了该方法的理论推导，并根据锥压和圆环侧压以及冲压试验获取材料应力-应变关系。本文基于Chen-Cai能量等效方法，针对圆弧漏斗薄片试样和圆环薄片试样，提出获取材料应力-应变关系的载荷-位移统一模型，通过单轴拉伸试验和变幅循环试验获得材料应力-应变关系与循环应力-应变关系。

1 载荷-位移关系统一模型

假定试样材料连续、均匀、各向同性、等向强化，采用Ramberg-Osgood幂律模型描述单调加载下的材料应力-应变关系，即

(1)

式中：ε、εe和εp分别为总应变、弹性应变和塑性应变；σ为应力；E为弹性模量；K为应力强度系数；n为应变硬化指数。

对于符合Ramberg-Osgood律的材料，漏斗薄片试样和圆环薄片试样的测量位移h可近似表达为弹性位移he与塑性位移hp之和[27],即

h=he+hp

(2)

总应变能可表达为

U=Ue+Up

(3)

式中：Ue为应变能弹性分量;Up为应变能塑性分量。

1.1 弹性应变能模型

在线弹性条件下，漏斗和圆环薄片试样末端在轴向载荷P作用下产生弹性位移量为he，由量纲相似原理，可以假设变形域内的弹性应变能与轴向位移的平方成正比[28]，则弹性应变能可表为

(4)

式中：k0为弹性系数。假设包含主要变形的规则几何区域为变形域，用Ω表示，如图1所示。选取Ω中能代表形状变化的几何参量为特征长度，用h*表示，本文中h*选为圆弧漏斗试样的缺口半径及圆环薄片试样外半径R；变形域的特征体积用V*表示，V*=h*A*；A*表示特征面积，对漏斗试样A*=(2w-πR)t，w为工作段宽度，t为试样厚度;对圆环薄片试样，A*=π(R2-r2)t/R，r为试样内半径。如图1所示的漏斗和圆环薄片试样工作段几何构形，加载线的A端为固定端，B端采用位移加载。

在准静态下，载荷做功不考虑热耗散，则

(5)

图1 漏斗薄片试样与圆环薄片试样工作段构形图Fig.1 Configuration of working sections of sheet-funnel specimen and sheet-ring spcimen

式中：We为载荷P作用下所做的弹性功。对式(5)求导

(6)

结合式(4)和式(6)，可得弹性条件下载荷-位移关系为

(7)

式中：弹性系数k0为与试样构形几何尺寸相关的函数，试样构形用几何因子λ表示，且λ=w/R。经过基于有限元方法的简单分析可知，弹性系数与几何因子满足抛物律关系,即

k0=a1λ2+a2λ+a3

(8)

其中：a1、a2、a3为待定常数。

1.2 塑性应变能模型

假设材料本构关系符合Ramberg-Osgood关系式(1)中的塑性分量式，即εp=(σ/K)n。变形域内任一点坐标可以用(x,y,z)表示，那么该点所在材料代表性单元(Representative Volume Element, RVE)的应变能密度记为u(x,y,z)，则Ω域的塑性应变能可表示为

(9)

式中：up为试样的塑性应变能密度。根据Chen-Cai能量等效方法[24]，能量中心的点(xm,ym,zm)处RVE的塑性应变能密度upm可表示为

(10)

则式(9)所示的Ω域内的塑性应变能Up可简单表示为

(11)

若以体积系数k1表示Ω域体积V与特征体积V*的比值，即

(12)

并假定等效塑性应变εp-eq与无量纲塑性位移hp/h*符合线性关系

(13)

式中：k2为塑性应变系数，将式(12)和式(13)代入式(11)，塑性应变能Up与无量纲塑性位移hp/h*满足以下关系

(14)

假设Wp为载荷P作用下的塑性功，在不考虑加载热损失的情况下

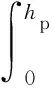
(15)

由式(14)和式(15)及V*=h*A*，可得P与hp之间的关系式为

(16)

进一步简化为

(17)

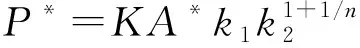
(18)

式中：b1、b2、b3、c1、c2、c3为待定常数。

1.3 载荷-位移统一模型

结合式(2)、式(7)和式(19)，整理可得漏斗和圆环薄片试样的载荷-位移统一模型

(19)

式中：k与材料常数(K，n)、弹性模量E和几何因子λ有关;P*与弹性几何因子λ、漏斗和圆环薄片试样半径R和材料常数K有关。漏斗薄片试样几何因子λ=w/R，且λ∈(2.75，4)；对于圆环薄片试样，λ=r/R，且λ∈(0.48，0.72)，并定义圆环薄片试样拉伸连接段工作带宽度为S，S=4(R-r)，过渡圆弧半径rt=r/4。

由于试样的厚度方向尺寸远小于长度、宽度方向，基本符合平面应力假设，有限元计算采用带厚度的Plane183平面应力单元进行计算，单元最小尺寸为1 μm，共2 500个单元。将该模型上端固定，下端采用位移加载，加载位移为0.1 mm。

鉴于模型的无量纲特性，设定弹性模量为E=200 GPa，采用有限元平面应力模型进行简单的纯弹性计算，即根据式(7)可确定弹性系数k0。如取he为漏斗薄片试样的加载线上弹性位移，则k0随λ的变化规律如图2(a)所示，可得a1、a2、a3分别为0、-0.009 74、0.092 6。为了测量方便，如Wisner等[19]，也常选取漏斗试样横向位移计算，系数k0与泊松比υ有关，所以k0/υ与λ的变化规律如图2(b)所示，从而确定了参数a1、a2、a3的取值分别为-0.002 06υ、0.001 15υ、0.012 2υ。

拟定强度系数K=1 000 MPa，硬化指数n=5，采用纯塑性计算确定体积系数k1和塑性应变系数k2，同样选取漏斗试样加载线位移可得式(18)中b1、b2、b3及c1、c2、c3的值，如图3所示。

事实上，如图1所示的加载线(A-B)位移对载荷引起的非线性敏感性弱，根据实际试验测量条件，往往采用跨漏斗圆弧两侧(C-D)位移和漏斗腰部横向(E-F)位移作为测量目标。对于圆环薄片试样的加载线(A-B)位移和圆环横向(P-Q)位移，根据有限元计算确定系数k0、k1、k2，所以两种试样的系数参数如表1所示。

图2 弹性系数k0、k0/υ与几何因子λ的关系曲线Fig.2 Relation between elastic coefficient k0, k0/υ and geometric factor λ

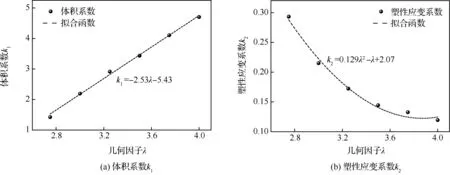
图3 系数k1、k2与几何因子λ的关系曲线Fig.3 Relation curves of coefficient k1, k2and geometric factor λ

表1 统一模型参数Table 1 Parameters of unified model

2 有限元验证

根据式(19)统一模型，定义应力-应变关系预测载荷-位移响应为正向预测，已知载荷-位移关系求材料应力-应变关系为反向预测。

2.1 正向预测验证

由于工程测试中，跨漏斗两侧位移比较方便测量，本文先取漏斗薄片试样的跨漏斗两侧位移进行验证。任选取一组试样的几何形状和材料属性进行有限元计算，如取试样缺口半径R=2 mm、弹性模量E为150～220 GPa、材料强度系数K为100～3000 MPa、塑性硬化指数n为2～20。简单计算可以得到对应的载荷-位移关系，称之为FEA(Finite Element Analysis)载荷-位移关系；通过统一模型也可预测出对应的载荷-位移关系，称为模型预测载荷-位移关系，经无量纲处理后的FEA载荷-位移关系曲线与模型预测载荷-位移关系曲线如图4所示，图4(a)～图4(d)分别表示变化不同参数的预测结果。

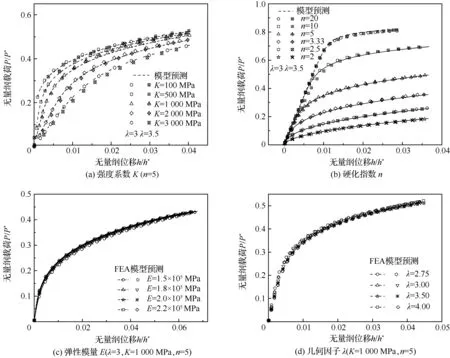
图4 漏斗薄片试样的P/P*-h/h*模型曲线与FEA计算曲线的对比Fig.4 Comparison of P/P*-h/h* model and FEA calculation curves of sheet-funnel specimen

经正向验证，模型预测的漏斗薄片试样P/P*-h/h*曲线与FEA计算曲线的结果基本一致。其中图4(a)对比了两种试样、同弹性模量、同硬化指数的前提下，改变强化系数的结果，强化系数越大，无量纲载荷越大；图4(b)为仅改变硬化指数，硬化指数越大，无量纲载荷越大；图4(c)仅变化弹性模量，分散性较小，弹性模量对P/P*-h/h*曲线的走势影响较小；在同一材料参数下，改变几何因子，如图4(d)所示，不同λ的P/P*-h/h*曲线吻合良好，表明模型预测曲线只与材料属性有关。所以在选取漏斗薄片试样的其他位移验证时，主要考虑材料塑性属性对曲线的影响，假定E=200 GPa、λ=3，验证当K=500、1 000 MPa时，不同硬化指数n对漏斗薄片试样加载线位移和漏斗根部横向塑性位移的P/P*-hp/h*曲线影响，如图5所示。

图5对比了薄片试样加载线位移和漏斗根部横向下的强度系数与同硬化指数对P/P*-hp/h*曲线影响。同硬化指数、不同强化系数的FEA计算曲线均能重合于同一条模型预测曲线；硬化指数越大，曲线走势越高。同时图5(b)显示，当选取漏斗根部横向位移时的预测结果并不敏感，且硬化指数较大时，预测结果偏差很大，所以硬化强度低的材料不适于测量漏斗试样横向位移进行试验。

图5 漏斗薄片试样的P/P*-hp/h*模型曲线与FEA计算曲线的对比Fig.5 Comparison of P/P*-hp/h*model and FEA calculation curve of sheet funnel-specimen

根据漏斗试样验证结果，只需计算材料的不同硬化指数n对圆环薄片试样模型预测与FEA计算的P/P*-hp/h*曲线的影响，如图6所示，即完成统一模型正向验证。

经有限元计算的正向预测结果表明：统一模型理论预测对漏斗薄片试样与圆环薄片试样的不同位置位移均适用，且在同一选取的位移尺度下的P/P*-h/h*曲线只与材料属性有关。

图6 圆环薄片试样模型预测与FEA计算的P/P*-hp/h*曲线对比Fig.6 Comparison of P/P*-hp/h* curves between model prediction and FEA calculation of sheet-ring specimen

2.2 反向预测验证

选取合适的Ramberg-Osgood模型参数(E，K,n)组合，经简单有限元计算获取载荷P与漏斗两侧位移hf的关系。对P-h关系曲线的线性段用函数P=ηhe拟合，η表示直线段斜率，由式(7)得到该材料的弹性模量E。根据hp=h-he可得到P-hp曲线，用函数P=P*(hp)m拟合P-hp曲线，可由式(17)得到该材料的塑性参量强度系数K、硬化指数n，应力-应变关系参数为

(20)

根据式(20)所得的参数代入式(1)，由载荷-位移关系反向预测应力-应变关系。选取跨漏斗薄片试样两侧的位移，针对不同材料属性、不同几何因子完成理论模型预测。输入弹塑性应力-应变关系，经有限元计算得到载荷-位移关系，通过该载荷-位移关系经模型反向预测的应力-应变关系，并将其与输入FEA的应力-应变曲线进行比较，如图7所示，图7(a)～图7(d)表示不同参数对比结果。

经过反向预测比较，统一模型的预测应力-应变曲线与FEA计算输入曲线基本一致。图7(a)和图7(b)分别对比了不同强度系数K和硬化指数n的模型预测应力-应变关系曲线，与FEA输入应力-应变曲线对比结果，K越大曲线趋势越高，n越大曲线越高，且曲线后半段越平；不同弹性模量的曲线分散性小，如图7(c)所示，弹性模量E对模型预测应力-应变关系的影响较小；图7(d)显示同一材料属性、不同几何构型反向预测的应力-应变曲线，均能重合与同一FEA应力-应变曲线，反向预测结果与几何因子无关。

图7 漏斗薄片试样模型预测σ-ε曲线与FEA计算输入曲线对比Fig.7 Comparison of σ-ε model and FEA calculation curves of sheet-funnel specimen

为对比不同试样构形与不同位移选取的应力-应变关系预测结果，其中包括漏斗薄片试样的跨漏斗两侧轴向位移、加载线位移与薄片圆环的加载线位移、圆环横向位移。对相同材料属性完成对上述的不同位移的预测，如图8所示，是选取弹性模量E=200 GPa、强度系数K=1 000 MPa与硬化指数n=5时的预测结果。

采用不同试样构形及位移反向预测的应力-应变曲线与FEA应力-应变曲线基本一致，所以采用漏斗薄片试样的跨漏斗两侧轴向位移、加载线位移与薄片圆环的加载线位移、圆环横向位移均能准确预测材料的应力-应变关系。

图8 不同的试样构形模型预测σ-ε曲线与FEA计算输入曲线对比(K=1 000 MPa)Fig.8 Comparison of predictions of σ-ε and FEA calculation input curves by different configurations (K=1 000 MPa)

3 试验与结果

3.1 试验条件

GH4169是一种新型高温合金材料，对应进口材料美国牌号为Inconel 718，主要成分: Ni 50%～55%、Cr 17%～21%、Nb 5%～5.5%、Mo 2.8%～3.3%、Ti 0.75%～1.15%、Co ≤1%、Mn ≤0.35%、Si ≤0.35%、 Cu ≤0.3%。由于其强度高、耐高温、并有较好延性，且具有良好的高温强度、加工硬化性及焊接性，在航空工程飞机叶片及核电工程密封环等关键领域中应用广泛。

设计漏斗薄片试样与圆环薄片试样如图9所示，试样尺寸为元币大小，设计长度H=24 mm、总宽度L=10 mm、厚度t=0.5 mm，两端夹持，中间为工作段，其宽度w=3.6 mm、圆弧漏斗半径R=1.2 mm，而圆环薄片试样外径R=2.5 mm、内径r=1.7 mm、工作段宽度S=3.2 mm、过渡圆弧半径rt=1 mm。

图9 薄片试样构形图Fig.9 Shape diagram of thin slice specimen

薄片试样的对称循环试验是采用Care IBTC-300原位双向拉压疲劳试验机完成的，设备的载荷量程1 kN；利用632.29F-30 引伸计实现了轴向应变测控，其标距为5 mm，测量范围-10%～30%，试样及引伸计装置如图10所示。单轴拉伸速率为0.001 mm·s-1，变幅循环试验采用控制应变幅自低到高分级加载，每500微应变为一级，每级应变幅下分别循环100周，加载波形为三角波，加载速率为0.002 mm·mm-1·s-1。

采用直径为4 mm的等直圆棒试样作为比对试样，单轴拉伸试样等直段为32 mm，疲劳试样等直段长8 mm。采用美国MTS 809电液伺服材料试验机，载荷量程为250 kN,控制系统为TestStarⅡ，应用软件为MTS790.10/SX，引伸计采用MTS 632.29F-30(标距为5 mm，测量范围-10%～30%)实现轴向应变控制。

图10 圆环薄片试样试验装置图Fig.10 Test device for sheet-ring specimen

3.2 材料应力-应变获取

完成单轴拉伸试验，分别测量跨漏斗试样两侧位移和圆环试样外的加载线位移，并获取两种试样的载荷-位移曲线如图11所示。

根据以上两种试样的载荷-位移曲线，经反向预测可以获取应力-应变曲线，与比对试样比较结果如图12所示。

比较图12，经漏斗薄片试样与圆环薄片试样预测的单轴应力-应变关系与对比试样试验结果基本重合。根据图12可以得到，材料弹性模量E=204 GPa，采用Ramberg-Osgood本构模型描述得到强度系数K=1 540 MPa、硬化指数n=18.1。

图11 漏斗薄片试样和圆环薄片试样载荷-位移曲线Fig.11 Load-displacement curves of sheet-funnel specimen and sheet-ring specimen

图12 单轴拉伸应力-应变关系曲线Fig.12 Stress-strain relation curve of uniaxial tension

3.3 循环应力-应变关系预测

完成了漏斗薄片试样与圆环薄片试样及对比试样的增幅循环试验，取每级循环中间次数的稳定载荷-位移曲线为载荷-位移滞回环曲线，连接各级滞回曲线尖点为循环载荷-位移曲线，漏斗薄片试样与圆环薄片试样的循环载荷-位移曲线如图13所示。

获取等直试样的循环应力-应变滞回曲线,定义最大应变回环的上升段为循环应力-应变特征曲线,如图14所示。

根据图14显示，特征曲线基本过应力-应变滞回曲线尖点，该材料大致符合Masing效应。漏斗薄片试样与圆环薄片试样的循环载荷-位移曲线，并与对比试样的循环应力-应变曲线和单轴应力-应变曲线比对如图15所示。

比较图15的循环应力-应变曲线，反向预测漏斗薄片试样与圆环薄片试样的循环应力-应变曲线与比对试样的循环应力-应变曲线基本重合，说明在循环载荷下的应力-应变关系是唯一的，与几何构型无关。材料在循环载荷下的弹性模量E=197 GPa、 强度系数K=1 505 MPa、 硬化指数n=15.2。单轴拉伸应力-应变曲线明显高于循环应力-应变曲线，GH4169在常温条件下表现循环软化特征，而硬化程度稍有增强。

图13 漏斗薄片试样与圆环薄片试样的循环载荷-位移曲线Fig.13 Cyclic load-displacement curves of sheet-funnel specimen and sheet-ring specimen

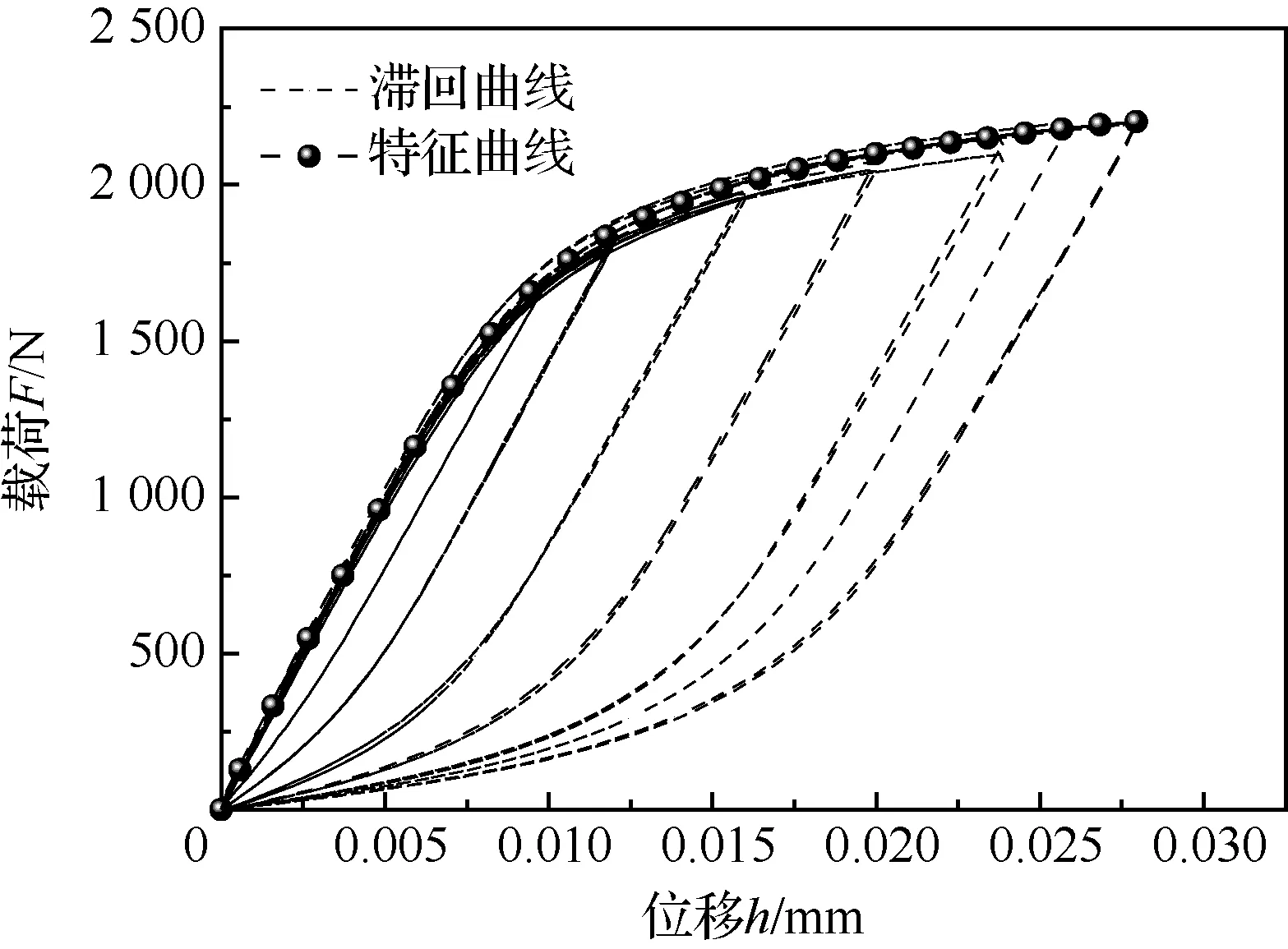
图14 对比试样应力-应变滞回环曲线Fig.14 Curres of stress-strain hysteresis loops of contrast specimens

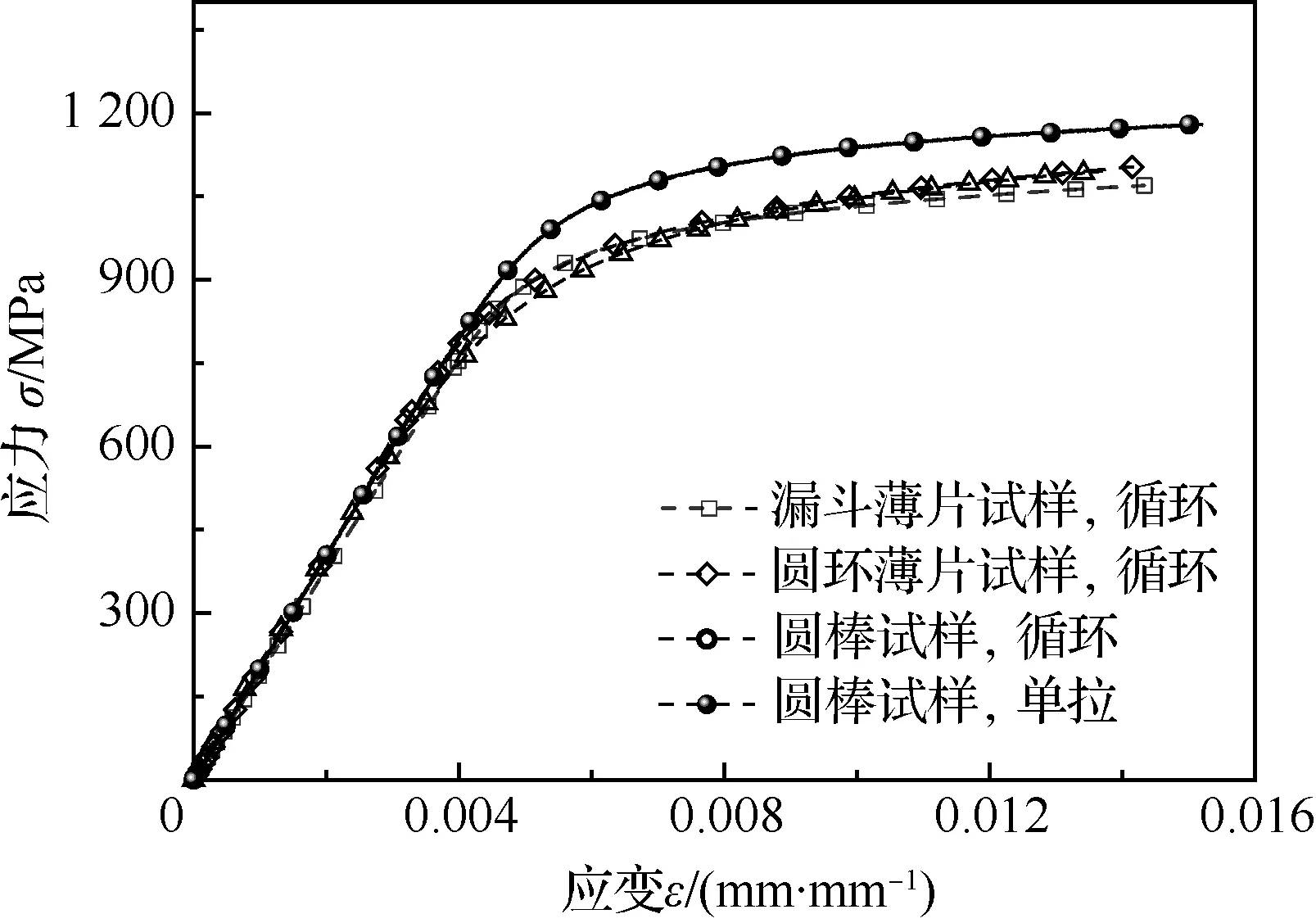
图15 循环应力-应变关系和单轴应力-应变关系曲线Fig.15 Relation curves of cyclic stress-strain and uniaxial stress-strain relation

4 结 论

1) 提出了基于漏斗薄片试样和圆环薄片试样获得单调应力-应变关系和符合Masing律材料的循环应力幅、循环应变幅关系的统一模型。

2) 在几何因子λ∈(2.75，4)范围内，经有限元正、反向验证表明，对漏斗薄片试样不同位移的统一模型均有良好普适性；该模型对λ∈(0.48，0.72)的圆环薄片试样同样适用。

3) 经漏斗薄片试样和圆环薄片试样获取的应力-应变关系曲线和循环应力-应变曲线，均与等直试样在单调载荷下获取的应力-应变关系和循环加载下的循环应力-应变曲线基本保持一致。

4) 材料循环应力-应变曲线的获取是完成材料疲劳寿命预测和抗疲劳设计的关键，本文统一半解析模型可为实现以毫米级薄片试样预测低周疲劳寿命提供新方法。