差别依赖验证的分布式算法

覃 昇 谈子敬 肖永松

(复旦大学计算机科学技术学院 上海 200433)

0 引 言

数据质量问题在大数据时代变得更为突出。无论系统能够以多么快的速度处理多么大的数据量，如果数据质量得不到保证，一切得到的分析结果可能都是无意义的。在对数据质量进行评估的多个维度中，数据一致性是一个常见的指标。数据一致性通常基于用逻辑表达式的形式所给出的数据依赖来进行描述。简而言之，若数据不满足给定的数据依赖，则称该数据为不一致，这通常意味着数据中存在错误或误差。

因为数据依赖的重要性，有大量的研究针对各种数据依赖展开。常见的数据依赖多数强调的是数据间的相等关系，例如函数依赖、条件函数依赖[1]等。在现实中，相关数据之间可能存在一定差异，而并非严格完全相等，也可能需要在依赖定义中引入大于、小于等序列关系。差别依赖[2]是一个表达能力较强的数据依赖定义形式，它满足了以上这些需求。常见的函数依赖是差别依赖的一个特例。

在数据一致性的相关工作中，数据集上的数据依赖验证是一个基础且重要的步骤：其目标是在数据集中找到不满足数据依赖的部分数据，以对其进行进一步的分析和修复。随着数据量的变大，数据依赖验证所需的内存和对处理器的要求越来越高，单机无法实现。这需要引入分布式计算技术，将问题并行处理。和单机算法不同，分布式算法需将整个问题分成若干个可并行的子问题，每个子问题由一台计算机作为一个节点(reducer)进行并行处理，最终整合结果。和设计单机算法只注重时间空间消耗不同，设计一个分布式算法需要考虑的主要因素，包括如何将问题尽可能平均地并行化分解；如何在保证正确的情况下减少并发运行时间，同时减少分发和收集过程中的数据量等。

本文研究的问题是：基于大规模分布式计算平台，在数据集上进行分布式差别依赖的验证。算法将基于差别依赖的特征，对部分情况进行优化，以提出更优的算法。

1 背景知识

1.1 差别依赖

首先回顾一下差别依赖的具体定义[2]。

对于关系数据表R中的一个属性B，在其值域dom(B)上定义一个二元差别dB(a,b)(a,b∈dom(B))。这个二元差别满足：(1) 非负性：dB(a,b)≥0，dB(a,b)=0当且仅当a=b；(2) 对称性：dB(a,b)=dB(b,a)。例如，实数域上的绝对值运算dB(a,b)=|a-b|是一个符合上述要求的二元差别，字符串的最小编辑距离也同样属于二元差别。

对于多属性上的差别函数φ[Z]，其中Z为若干个属性组成的集合。则有：

(1)

定义2一个数据表R的差别依赖DD，其形式为:

DD:φ1(X)→φ2(Y)

(2)

其中：X、Y是R中属性集的子集，φ1(X)和φ2(Y)是两个不同的差别函数。

对一个信用卡交易的数据库，可以有如下差别依赖：

DD1[cardno(= 0)]∩[position(≥60)]→[transtime(≥20)]

其含义为：当两笔交易的卡号(cardno)相同，并且发生地点(position)相距不小于60时，则这两笔交易的时间(transtime)一定不小于20。

对于一个产品价格记录的数据库，可能有如下约束：当两条记录的日期(date)相距在7～30天时，则价格之差将在100～900的范围内，其表达式为：

DD2[date(>7,≤30)]→[price(≥100,≤900)]

可以看到，差别依赖是一个具有较强表达能力的依赖类型，并且函数依赖是它的一个特例。由差别依赖的定义可知，差别依赖的约束验证，需要对数据集中的任意元组对进行比较。该算法的复杂度是元组个数的平方。当数据集具有较大规模时，单机的内存和时间将无法承受该负荷，所以使用分布式系统进行差别依赖的验证。

1.2 分布式系统及算法

在MapReduce[3]和Spark系统中，一个分布式系统由若干无共享存储空间的计算机构成，每一台计算机被视作一个节点(reducer)，所有节点之间的交互通过网络中的发送和收集信息来实现。一个分布式算法由若干轮映射归约(MapReduce)操作组成，每一轮操作分为映射(Map)、转移(Shuffle)和归约(Reduce)三部分。其中：Map为数据传输做准备，产生包含数据内容的键值对(Key-Value)；Shuffle根据数据的键值进行实际的数据传输，使得所有键值相同的数据被归约到同一个节点；当每一个reducer将具有相同键值的数据收集之后，便继续完成Reduce中之后的步骤，可能进行统计或输出，也可能开始下一轮的MapReduce操作。三个操作之中，以Map和Reduce为算法核心。

1.3 分布式验证相关工作

文献[4]中主要讨论了当数据表以水平分割或垂直分割的形式存储时，如何进行条件函数依赖的检验，使得数据传输量或并发运行时间最小。文献[5]中提出了一种基于等价类的分布式环境多函数依赖冲突检测的方法，给出了冲突检测的响应时间代价模型，并且将问题化为整数规划问题，给出近似解。文献[6]中提出了一种分布式环境多函数依赖不一致性检测方法，依靠最小集合覆盖的理论，通过一次数据遍历，对多个函数依赖进行并行检测。文献[7]中将数据依赖的检测和数据清洗化归为一系列的原子操作，并针对多操作提出了并行或合并的改进。

本文研究的是差别依赖在分布式环境下的验证。如前所述，差别依赖不仅包括函数依赖，还包括一系列建立在不相等或相近的数据上的依赖条件。本文的算法设计考虑了差别依赖的定义形式，同时针对部分的数据分布特征，进一步给出优化策略。

2 三角分布算法

差别依赖的验证基于表中元组的两两比较、直观理解，这和数据库中一个表上的自连接(join)运算有相似之处。在分布式的设定下，为了实现元组的两两比较，并且保证不重复、不遗漏以及时间上的可接受，需要一定的运算技巧。文献[8]针对大数据下元组的查重问题，使用了一种三角形分布的算法。算法的本质是模仿向量的叉乘，同时根据运算的对称性，删去其中约一半的运算。从结果上看，三角分布算法是将reducer排列成一个三角形，元组根据一定要求，通过MapReduce算法，分发到对应的reducer中。该算法不仅保证了正确性和比较次数的最优化，同时也保证了每一台机器的时间复杂度都相同。

以文献[8]中的方法为基础，本文给出一个适用于差别依赖检测的随机三角发表算法。

2.1 随机三角算法

当reducer数目给定时，比如为m，取最大的正整数l，使得l(l+1)/2≤m成立，此时l为三角分布的边长。图1为m=21、l=6的情况，其中每一个小方块表示一个reducer，左上角的数字为其编号。按照图1对每行每列进行编号，每一台reducer可以由一个整数对来表示。例如编号为9的reducer同样可以表示为(4，2)。

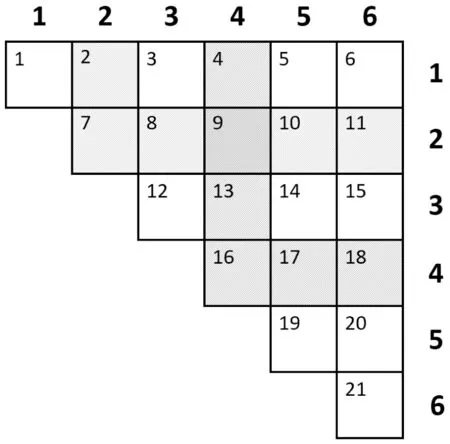
图1 三角分布节点示意图

利用三角分布策略，可以有效实现元组的成对比较，其具体算法见算法1。

算法1随机三角分布算法

输入：数据表的元组t；

三角分布边长l；

差别依赖DD。

输出：违背DD的所有元组对。

1: class MAPPER

2: method MAP(Tuple t)

3: Iht a ← a random value from [1,l]

4: for all p∈[1,a) do

5: EMIT(Reducer(p,a),(L,Tuple t))

6: EMIT(Reducer(a,a),(S,Tuple t))

7: for all q∈(a,I] do

8: EMIT(Reducer(a,q),(R,TupIe t))

9: class Partitioner

10: method PARTITION(Key rid,Pair(c,t))

11: Return rid

12: class REDUCER

13: method REDUCE(Key rid,Pairs[(c1,t1),(c2,t2)…])

14: Left,Right,Self ← Ø

15: for all Pair (c,t)∈Pairs[(c1,t1),(c2,t2)…〗

16: if (c=L) then Left ← Left+t

17: else if (c=R) then Right ← Right+t

18: else if (c=S) then Self ← Self+t

19: if Self ≠ Ø then

20: for all t1∈Self do

21: for aIl t2∈Self do

22: check t1and t2

23: else

24: for all t1∈Left do

25: for all t2∈Right do

26 : check t1and t2

27: Return Pairs(t1,t2) violating the DD

整个算法建立在分布式结构中，共有一次MapReduce操作，包含Map、Shuffle和Reduce三个阶段。

在Map阶段(第1-8行)，对每一个元组，选取一个1到l的随机数a(第3行)，将元组发射到第a行和第a列的所有reducer中(第4-8行)。发射的过程中，需要进行标记，例如一个元组的随机数为4，则在发送到第4列的4、9、13号机器上时，标记为L；发送到对角线上的16号机器上时，标记为S；发送到第4行的17、18号机器上时，标记为R。

在Shuffle阶段(第9-11行)，数据根据机器序号进行分组。

在Reduce阶段(第12-27行)，每一台非对角线上的机器，接收到标记为L和R的两类数据(第16-17行)，双重循环比较L和R集合之间的元组对(第23-26行)，是否符合需要验证的差别依赖；而在对角线上的机器，则只会收到标记为S的数据(第18行)，收集之后对其内部的所有元组对进行两两比较(第19-22行)。全部比较结束之后，返回违背DD的元组对(第27行)。

2.2 算法正确性和时间复杂度

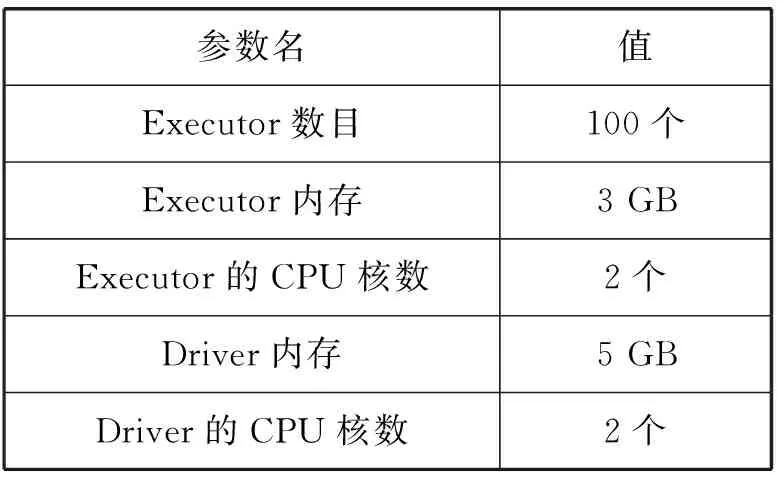
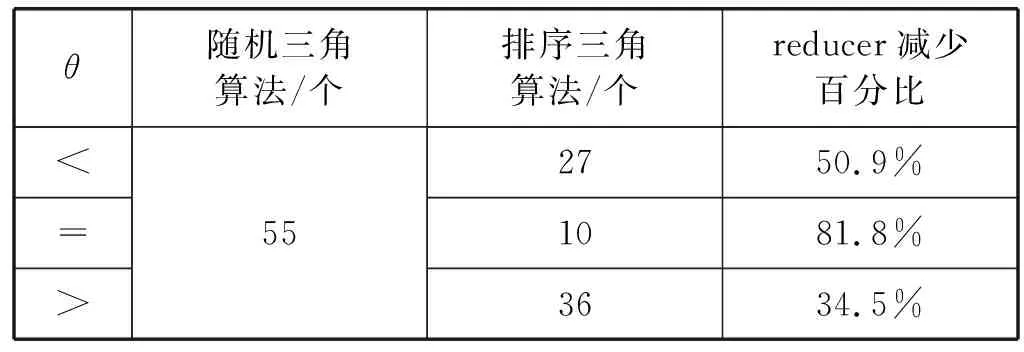
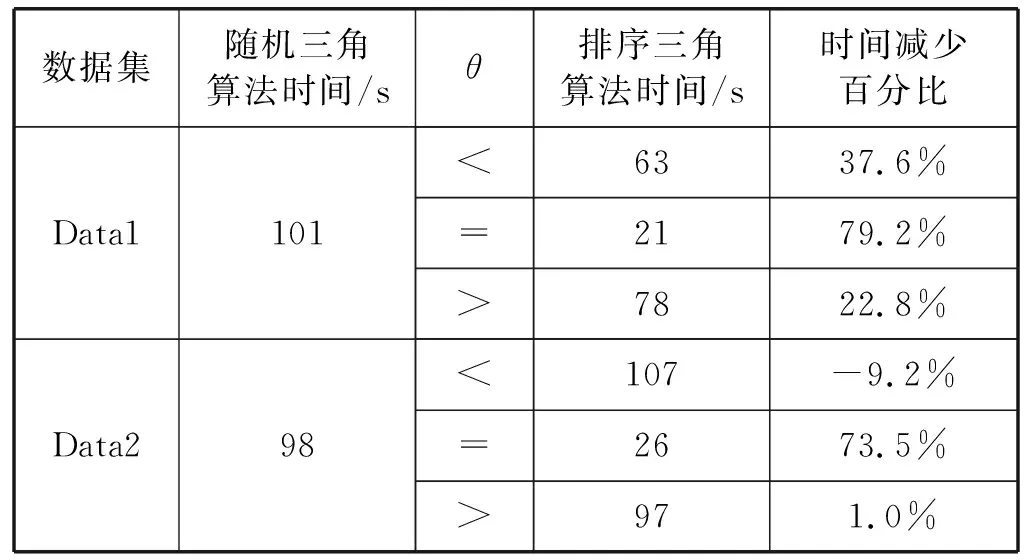
算法的正确性等价于任意两条元组都必须进行过比较。对于任意两条元组，设它们在第3行得到的随机数为i和j，由于差别依赖具有对称性，设i≤j。若i=j时，元组会在机器(i,i)上进行比较；若i

从时间上看，算法的整体耗时主要集中在Reduce阶段的数据比较上。设元组总数为n，则取到相同随机数的元组个数平均值为n/l。

对于非对角线上的机器，其L和R集合中的元素数量均为n/l，所以总比较次数为n2/l2；

对于对角线上的机器，其S集合中元素数量为n/l，所以总比较次数为n2/l2；考虑到差别依赖的对称性，(t1,t2)和(t2,t1)的比较完全一致，所以总比较次数可以减少至n2/2t2。

综上，三角分布策略时间复杂度为O(n2/l2)，并且每一台机器上的时间平均复杂度相同。

2.3 排序三角算法

对于一部分数据集，其在某些属性上的值的上下界是已知的，并且分布大致均匀。若能通过这些已有的信息，在Map过程中就进行初筛，则可以减少部分运算时间。基于这样的想法，可以对部分数据集上的差别依赖的检验，使用如下的排序三角算法。

考虑一条左侧含有[A(θp)]的差别依赖，其中A是属性，θ是判断运算符(θ∈{≥,>,=,<,≤)，p是常数。同时A属性的值存在上下界，大致地均匀分布在区间[smin,smax]中。令:

(3)

t表示单位区间长度，则整个[smin,smax)区间可以被分成l个长度为t的单位区间。在算法1中，a为1到l中的随机数(算法1第3行)，而在排序三角算法中，a的取值为:

(4)

式中：t[A]为该元组在A属性上的取值，则a∈[1,l]，并且所有元组被有序分散到reducer中。令k=p/t，则可以根据k的值免去部分reducer上的元组比较。

如图2所示，取k=1，l=4。记difi为在编号为i的reducer中，需要比较的两个元组的属性A上值的差的范围。例如dif7=(p,3p)，因为在这个reducer中需要比较的两个元组的A属性的值分别属于[3p,4p)和[p,2p)，所以两个数据之差的范围为(p,3p)。

图2 节点数据示意图

图3显示了在图2条件下各reducer中可能进行的运算，显然针对特定的θ,并非所有reducer都有工作。记numθ为θ取不同运算符时所需要的reducer数量，在忽略少量的边界情况和暂定k为整数时，计算可得：

num≤=num<=(l+l-k)(k+1)/2

(5)

num==l-k

(6)

num≥=num>=(l-k)(l-k+1)/2

(7)

图3 各节点和运算符的对应关系

当初始条件都给定时，可以计算出对应的numθ，所以只需要这些数量的reducer工作就可以完成所有的比较，剩下的reducer无需运行。所以可以在map阶段，直接减少数据的发射量，数据发射(emit)时，若目标reducer不需要进行运算，则可以跳过这个当前的发射步骤，减少Shuffle阶段的数据运输量。

另一方面，既然可以减少需要使用的reducer，那自然也可以用这些reducer来加速整个过程。

在已知reducer数目情况下(数目为m)，可以令边长l′为变量，根据之前k和numθ的定义式，解出满足numθ≤m的最大l′值，显然有l′≥l。当三角分布边长从l变大到l′以后，由于每一台机器分配到的运算量的复杂度相同，而总运算量不变，所以每一台使用到的机器上分到的运算量会相应变少，总时间减少。

如果k=p/t不为整数，则需要在上述numθ的基础上进行一定的增加。从图2中可以看出，若k=1.5，θ取<，则编号为3和7的reducer同样需要进行运算，num<会增大。在这个情况下，在一部分的行上需要额外增加一个reducer，所以每个numθ都会增加，增加的数目上界为l。在这些额外加入的reducer中，并不是所有的元组对都符合[A(θp)]，所以还需要进行检验。

3 实验分析

实验使用的分布式环境是Spark 2.0.0，主要的启动参数见表1。

表1 Spark启动参数表

实验所使用的测试数据集有两个，均为人为构造的大数据集。两个数据集均含有属性A，该属性的值域为[0,100)，不同点在于，数据集Data1在属性A上的值为均匀分布，数据集Data2在属性A上的值呈正态分布，平均值为50，方差为20，即在[30,70]范围内包含了总数据的约70%。

在实验1和实验2中，只使用Data1作为测试数据测试三角算法的性能，而在实验3中，使用Data1和Data2作为测试数据，比较随机三角算法和排序三角算法的优缺点。

实验所使用的差别依赖DD，其左侧共有两个差别函数，其中包含有差别函数φ(A)=[A(θ,30)]。在实验1和2中，指定θ为<，在实验3中，将取θ分别为<、=和>，进行两种三角分布的性能比较。

3.1 时间比较

目前在分布式平台上，用来处理结构化数据的常见工具有SparkSQL和Hive。

SparkSQL是Spark上的一个模块，可以从外部读入数据内容，将其转化为特有的DataFrame数据结构，分布式地进行存储和运算。同时它包含了部分数据库常见的操作函数，可在分布式平台上进行用户的查询或修改操作。

Hive是基于分布式平台的一个数据仓库工具，可以将结构化的数据文件映射为一张数据库表。在Hive上可以进行结构化查询语言SQL的语句查询。当输入SQL语句之后，Hive会把SQL语句转换为MapReduce任务，然后在分布式系统上进行运行。

通过将差别约束的验证改写为SQL语句，在Hive和SparkSQL下运行。

例如，在表格Table1上有差分依赖：

DD3[A(> 10)]→[B≤20)]

现需要返回违背DD3的元组对的数量，可以用如下SQL语句来描述：

SELECT COUNT(*)

FROM Table AS X,Table AS Y

WHERE(X.A-Y.A)>10 AND ABS(X.B-Y.B)>20

实验1使用随机三角分布、SparkSQL和Hive进行差别依赖的验证，比较不同数据量下的时间。此处三角分布的边长取l=14。

需要注意的是，由于Hive的运行时间过长，图4中使用了对数纵坐标来显示运行时间，横坐标为实验数据集的元组个数。当数据量为20万行时，Hive的执行时间已经超过了7个小时，由此省略了40万行时Hive的运行结果。从图4可知，三角算法的时间非常快，是SparkSQL和Hive时间的1/10～1/100。当数据量达到40万行时，SparkSQL的耗时已经达到了近2个小时，而三角分布只需要不到5分钟，时间优势非常明显。

图4 实验1的实验结果

3.2 不同边长下性能比较

以随机三角分布的边长和数据量作为变量，比较各情况下检验差别依赖所需要的时间。

观察图5中同一条曲线，当边长一定的时候，reducer数目不变，显然数据量的增加会导致总时间增加。另一方面，在同数据量的情况下，随着边长的增加，参与的reducer数目会增加，时间随之下降，这和预期一致。

图5 实验2的实验结果

需要注意reducer数目的增加并不会使得总时间一直下降。从实验结果看，当reducer数目已经较大时，再增加其数目(即增加边长)对继续缩短时间的帮助变得不再明显。这是因为中间的Shuffle过程是需要有实际的数据传输的。若过度增加边长和reducer数目，会造成数据传输量增大，而每个reducer上的工作减少却不明显，这可能反而会造成总时间的增加。

3.3 两种三角分布算法性能比较

排序三角算法相较于随机三角算法，可以在边长相同的情况下省去部分的reducer，或者可以增加reducer利用率，减少时间，但这两点都建立在数据分布较为平均的情况下。现对于两个数据集，进行两种算法的性能比较。

3.3.1 边长相同时reducer的减少

当边长固定时，随机三角算法的reducer数目是不变的，而排序三角算法需要的reducer数目可以通过计算得出。以边长l=10为例，计算得出θ取不同运算符时的reducer数量，和随机三角算法进行比较，如表2所示。

表2 reducer数目计算结果

分析表2得出，使用优化算法，对于同一个差别依赖，其使用的reducer数目得到了显著的下降，特别是在取值为=的时候。实际上，reducer可减少的数目与常数值和该属性的取值范围有很大关系：当常数值接近于属性值取值范围的中间值时，不论θ的取值多少，都可以减少很大占比的reducer数目；而当常数值接近于属性值的一端时，至少也有两个θ的取值可以使得reducer数目减少很多。

3.3.2 时间上的比较

排序三角算法相较于随机三角算法，依赖于原始数据的具体分布。虽然三角边长可以增大，但若原始数据分布不均匀，会使得某些机器上的比较次数变多，进而影响总体运行时间。本次实验的数据集为均匀分布数据集Data1和正态分布数据集Data2，行数为20万行；随机三角算法的边长l=10，与排序三角算法在θ的不同取值下进行比较，如表3所示。

表3 时间比较结果

由表3可得，在均匀分布的数据集上，排序三角分布算法非常出色，可以更加高效地利用所有的reducer进行计算。而在正态分布的数据集上，当运算符为<和>时，时间和随机分布的耗时差距不大。这说明排序三角算法相对来说依赖于初始数据和初始条件，以及此时的方差和的取值是采取何种三角分布算法的分界点。

对于排序三角算法，若数据分布不均匀，会导致部分reducer上的工作量超过平均值，而MapReduce算法的时间，依赖于所有reducer中最晚结束的时间，所以非平均数据集的排序三角算法的时间会长于使用相同数量reducer的随机三角算法的时间。对于一个数据集更适合于何种三角分布算法，可以先通过抽样来对数据分布进行分析。

另外，对比表2和表3可以得出，即使是均匀分布的数据，时间减少的百分比，也不如上一个实验中预估reducer减少的百分比。这主要是因为在之前的分析中，部分因素被忽略了：一部分原因是在Shuffle步骤的耗时是固定的(大致只与元组数量有关)，这部分时间无法按比例降低；另一方面，边长增加后，由于不为整数，所以也无法做到将所有的有效比较完全均匀分配到每一个reducer中，依旧会存在部分的冗余比较无法避免。

4 结 语

差别依赖用于描述数据表中元组对间属性变化量之间的关系。差别依赖的约束验证需进行元组的两两比较，通过引入分布式计算技术可以有效提高该过程的可用性。本文针对该问题进行研究，在分布式系统上提出了随机三角分布的分布式算法，实现了差别依赖的大数据检验。本文提出了排序三角分布，在均匀分布的数据集上，能够更快速高效地完成约束验证。通过实验，两个算法的时间优势非常明显。

在未来的工作中，本文将考虑多差别依赖的分布式检测算法。针对多依赖，通过合并检测的方式以减少重复的工作量。另外，经分析，数据传输量这一要素相对被忽略。在Spark等并行处理的系统中，Shuffle步骤会进行数据的传输，数据传输量在reducer间的分派情况也会实际影响到最终的总计算时间。我们将由此探讨边长、数据转移量以及时间上的关系，以期进一步进行算法优化。