灰色线性回归组合模型在中国出境旅游规模预测中的应用*

胡贝贝,王 莉,汪德根

(1.安徽师范大学 地理与旅游学院，安徽 芜湖 241000；2.苏州大学 建筑学院，江苏 苏州 215123)

中国出境旅游市场自2014年首次迈入“亿人次”时代，已连续四年成为世界第一大出境旅游消费国，对全球旅游收入贡献平均超过13%。2016年，中国出境旅游人次已达1.22亿人次，出境游花费达到1 098亿美元，人均花费约900美元。可见，中国出境旅游正持续呈现高速发展态势。出境旅游市场的蓬勃发展一方面有助于推动中国旅游市场的不断壮大，另一方面有助于提升中国在国际旅游领域的话语权，促进文化和价值观等软实力的输出以及增强与周边国家的良性互动。在此背景下，为有效把握出境旅游发展方向，及时调整出境旅游相关政策，合理预测出境旅游市场规模，对世界旅游业发展及中国旅游产业优化升级具有重要的战略性指导意义。其中，出境旅游市场预测是开展出境旅游一系列工作的基础，直接关系到中国出境旅游未来的发展方向、出境游政策和出境游市场供给等一系列决策问题的科学性。

一、相关研究综述

当前，关于旅游市场预测的研究主要集中在国内旅游市场和入境旅游市场两个领域，而对出境旅游市场预测研究相对较少，其研究方法主要集中在回归分析法、时间序列法、灰色预测法等定量分析法构建一系列单一统计预测模型，对旅游客流进行预测评估[1-2]。其中，灰色预测模型因其具有所需样本数少、贫信息、短期精度高、计算简便、具有可检验性等优点而被众多学者广泛应用到社会、经济、交通、环境等领域研究中[3-4]。灰色系统预测模型(Grey Dynamic Model,简称GM模型)是借助灰色系统理论构建的预测模型，通常运用少量已知的白化参数去预测未知信息(灰色信息)[5-6]。陈鹏依据2006—2011年安徽省旅游业相关数据，构建安徽省入境旅游灰色预测模型，并对安徽省“十二五”期间的入境人数进行了预测[7]。朱晓华等人利用1978年以来中国入境客源数据，构建了旅游客源预测的灰色模型和线性模型，并对两种预测模型的拟合精度进行了定量对比，得出了灰色GM(1，1)模型的数据拟合度和精度高于线性回归模型的结论[8]。刘慧敏等借助灰色系统理论，以2004—2008年广州市旅游接待人数为数据源，构建了灰色GM(1，1)预测模型，为提高模型的预测精度，对原始模型进行了改进，将其应用于广州市2009—2012的旅游接待人数预测中[9]。

由于中国出境旅游市场发展较晚，能收集到的数据有限，因此，可根据灰色预测模型所需数据少、精度高的特点，将灰色预测模型用于中国出境旅游客流规模预测中，以解决当前出境旅游新时代背景下历史数据少的问题。在实际运用中，由于旅游业较易受到经济、社会、文化、政策、气候等一系列不确定因素的干扰，具有较高的敏感性、动态性和复杂性，导致出境旅游客流数据的随机性和波动性都较大，仅利用单一灰色预测模型在对既有指数增长趋势同时又有一定的线性变化的原始数据进行拟合时，将会大大降低预测结果的精度，干扰预测的准确性。因此，在选择中国出境旅游客流规模的预测方法上应区别于一般系统的预测，出境旅游客流预测具有更明显的特殊性。20世纪60年代，Bates和Granger-tong将两种以上单一预测模型进行加权组合，通过对比分析后发现加权组合后的预测模型其预测结果的精度要远远高于每个单一模型预测结果，进而指出组合预测模型能有效克服单个预测模型的精度不够的局限性，成为现在广大领域研究和应用的主要趋势[10-11]。国内学者陈有为以我国城镇居民家庭人均购买鲜菜量为例，在传统的灰色预测模型基础上，将三次指数平滑预测模型和离散GM(1，1)预测模型进行加权组合后，对中国城镇居民家庭人均购买鲜菜量进行预测研究[12]。卢阳指出在利用传统GM(1，1)模型进行数据预测时，因忽略了原始数据的线性变化规律导致其预测效果不佳，因而在传统模型的基础上加入线性部分，构建了灰色线性组合金融预测模型，将其运用到金融的实例预测中，结果充分证实了优化后的组合预测模型具有较高的预测精度[13]。

综上，灰色预测模型已经在经济、金融、生态等领域得到了较成熟而广泛的应用，具有较高的理论价值和实际应用价值。为了对中国出境旅游客流规模进行精度更高的预测，本文借助灰色系统理论，基于线性回归和传统的灰色GM(1，1)预测模型，构建一种可行的出境旅游灰色线性回归组合预测模型，并对2017—2025年中国出境旅游客流规模进行了科学的预测，以期能够正确把握中国出境旅游市场发展规律和变动趋势，为中国出境旅游的可持续发展提供科学的依据。这里分析中国出境旅游市场仅指中国大陆居民，中国香港和澳门两个特别行政区，以及中国台湾省暂不纳入分析。

二、模型的构建与精度检验

(一)线性回归预测模型

线性回归模型是用一个或多个解释变量来解释因变量的一种计量模型。建立一元线性回归方程：

Y=α+β×x

(1)

其中，α为待定参数，β为常数项。

(二)灰色GM(1,1) 预测模型

首先，对原始灰色序列进行光滑性处理，通过作一次累加生成呈显著指数增长规律的时间序列；其次，将该时间序列通过灰色拟合方法转化为一介单变量系数微分方程,建立抽象系统的发展变化动态模型；最后，通过一次累减生成还原得到原始数列的预测值，从而将灰色问题淡化和白化。其建模的具体步骤如下：

生成灰色序列，假设中国居民出境旅游客流原始数列为X(0)：

X(0)=(X(0)(1),X(0)(2),…,X(0)(n))

(2)

对原始数列进行光滑性处理，作一次累加生成数列X(1)：

X(1)=(X(1)(1),X(1)(2),…,X(1)(n))

(3)

建立GM(1,1)灰色预测模型的线性灰微分方程：

(4)

其中a、b为待辨识参数，a为发展系数，b为灰作用量，可通过最小二乘法求出参数a和b的值，计算公式为：

(a,b)T=(BTB)-1BTY

(5)

其中，

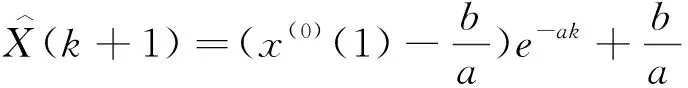
(6)

计算原始数列拟合值，根据时间响应函数对累加后的数列进行拟合，并对得到的拟合值进行累减即为原始数列X(0)的拟合值：

X(0)(k)=X(1)(k+1)-X(1)(k),(k=1,2,…,n-1)

(7)

(三)灰色线性回归组合预测模型

灰色线性组合预测模型是一种基于线性模型和灰色GM(1,1)预测模型形成的一种灰色预测优化模型，其能对不稳定的数据进行拟合较高的预测，具有较强的自适应性和动态预测特征，进而避免了线性回归预测和灰色GM(1,1)预测模型在对随机的、波动性较大的数据进行拟合预测时精度较低的缺点。构建步骤如下：

生成灰色序列，假设大陆居民出境旅游客流原始数列为X(0)：

X(0)=(X(0)(1),X(0)(2),…,X(0)(n))

(8)

对原始数列进行光滑性处理，作一次累加生成数列X(1)：

X(1)=(X(1)(1),X(1)(2),…,X(1)(n))

(9)

Z(k)=X(1)(k+1)-X(1)(k),(k=1,2,…，n)

(10)

再设：

ym(k)=Z(k+m)-Z(k),(m=1,2,…,n-3)

(11)

根据上式可得出：

ym(k)=C1e-Vk(evm-1)(ev-1)

(12)

那么有：

(13)

从而得到灰色线性回归组合预测模型中参数v的拟合值：

(14)

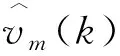
(15)

最后根据最小二乘法求出参数C1,C2,C3的值，计算公式为：

C=(ATA)-1ATX(1)

(16)

其中，

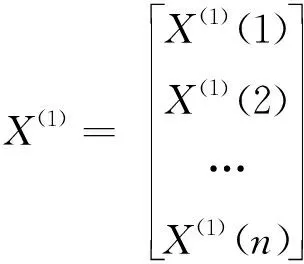
即得到灰色线性组合预测模型的时间响应函数：

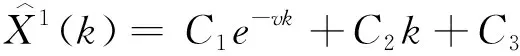
(17)

根据灰色线性组合预测模型的时间响应函数进行数值拟合，对得到的拟合数值进行一次累减，即为原始数列的模拟值或预测值。

(四)模型精度检验

为检验构建的线性回归预测模型、灰色GM(1,1)预测模型以及灰色线性回归组合预测模型是否适用于中国出境旅游客流规模的预测，并进一步比较三种模型的预测精度和拟合度的大小。本文采用残差检验和后验差检验两种方法对三种模型的可靠度进行检验。

1.模型的残差检验

计算出原始数据和预测数据的绝对误差ε(k)和相对误差Δk：

(18)

(19)

2.模型的后验差检验

计算出原始数列的方差s1和残差的方差s2，从而得到后验比C和小误差概率p：

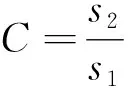
(20)

通过计算模型的后验比C和小误差概率p，对照模型精度表1中的C和p的取值范围，判断该模型是否合格。

表1 后验差检验模型精度表

三、中国出境旅游客流规模预测

本文以中国出境旅游客流为研究对象，收集了2010—2016年出境旅游客流量作为预测2017—2025年中国出境旅游客流规模的基础数据，数据来源于《中国旅游统计年鉴》和《中国旅游业统计公报》。使用收集到的出境旅游数据分别建立线性回归模型、灰色GM(1，1)模型及灰色线性回归组合模型。其中出境旅游客流数据的单位均为万人次。

(一)线性回归预测模型

根据2010—2016年出境游数据，建立线性回归方程为：

Y=1111.3x+4912.1

(21)

利用线性回归模型对2010—2016年的出境旅游规模进行预测，结果见表2。

(二)灰色GM(1，1)模型预测

根据已收集到的2010—2016年大陆居民出境旅游人数，生成出境旅游客流原始数列X(0)=(5738.65,7025,8318.17,9818.17,11659.32,11700,12200)，由最小二乘法可计算参数a，b的值为：

(22)

对时间响应函数进行一次累减可得到出境旅游灰色GM(1,1)预测模型为：

X(0)(k)=X(1)(k+1)-X(1)(k),(k=1,2,…,n-1)

(23)

利用灰色GM(1,1)模型对2010—2016年的出境旅游规模进行预测，结果见表2。

(三)灰色线性回归组合预测模型

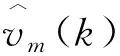
表2 三种预测模型的拟合和相对误差的对比

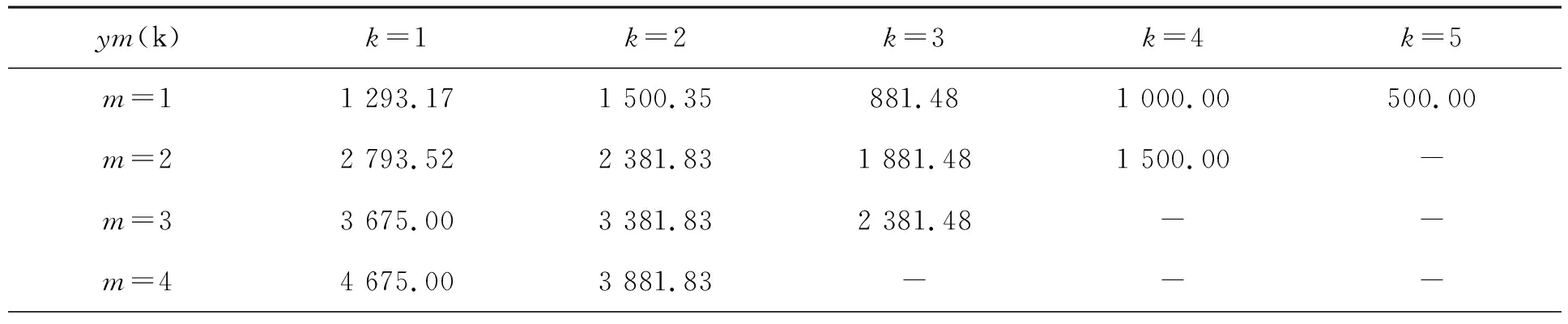
表3 不同m下ym(k)值

表4 不同m下的值

最后，建立出境旅游灰色线性回归组合预测模型的时间函数为：

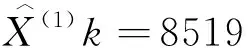
(24)

X(0)(k)=X(1)(k+1)-X(1)(k),(k=1,2,…,n-1)

(25)

利用灰色线性回归组合模型对2010—2016年中国出境旅游规模进行预测测度，结果见表2和图1。

(四)模型检验及评价

1.模型的残差检验

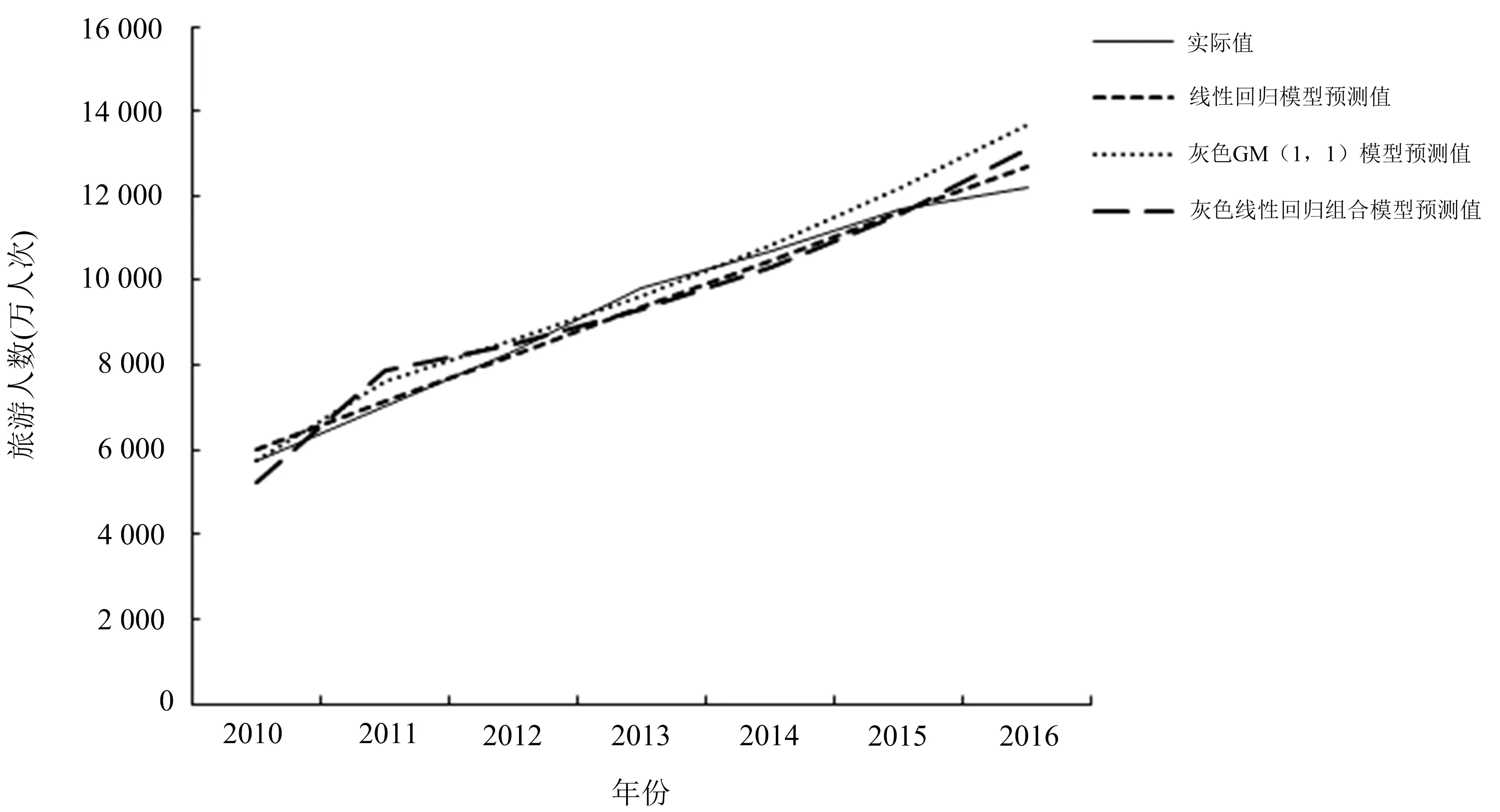
图1 三种预测模型对中国出境旅游客流规模预测结果的比较

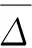
2.模型的后验差检验

由表5可知，线性回归预测模型、灰色GM(1，1)预测模型、灰色线性回归组合预测模型三种模型的小误差概率p均等于1，对照模型精度等级划分表1，可以判断小误差概率p的值均处在一级精度等级；通过计算可以得到模型的后验差比C分别为0.133、0.039、0.021，可以判断出境旅游灰色回归组合预测模型精度级别最高，为1级精度模型，灰色GM(1，1)预测模型其次，线性回归预测模型的精度最差。通过对三种模型的平均相对误差、小误差概率、后验差比检验后，综合对比分析可判断，灰色回归组合预测模型的精度最高，其预测结果具有较高的准确性和可信度。

表5 三种预测模型的精度检验对比

3.2017—2025年中国出境旅游客流预测与分析

根据上文分析结果，应用灰色线性回归组合预测模型对2017-2025年中国出境旅游客流量进行预测。从预测结果(见表6)来看，中国出境旅游客流在未来几年将继续保持增长的趋势，平均增长率达21%，2025年出境旅游总人数达将6.2亿人次。当一个国家的人均GDP达到1 000美元，旅游消费进入启动阶段，当人均GDP达到3 000美元时，出境旅游人口规模开始兴旺[14]。据2016年国际货币基金组织统计，中国人均GDP现已达到8 113美元，可见，中国的出境旅游正处于大发展时期。随着人们生活水平的提高，对出境旅游需求不断增长，未来出境旅游规模将会以更快的速度扩大。

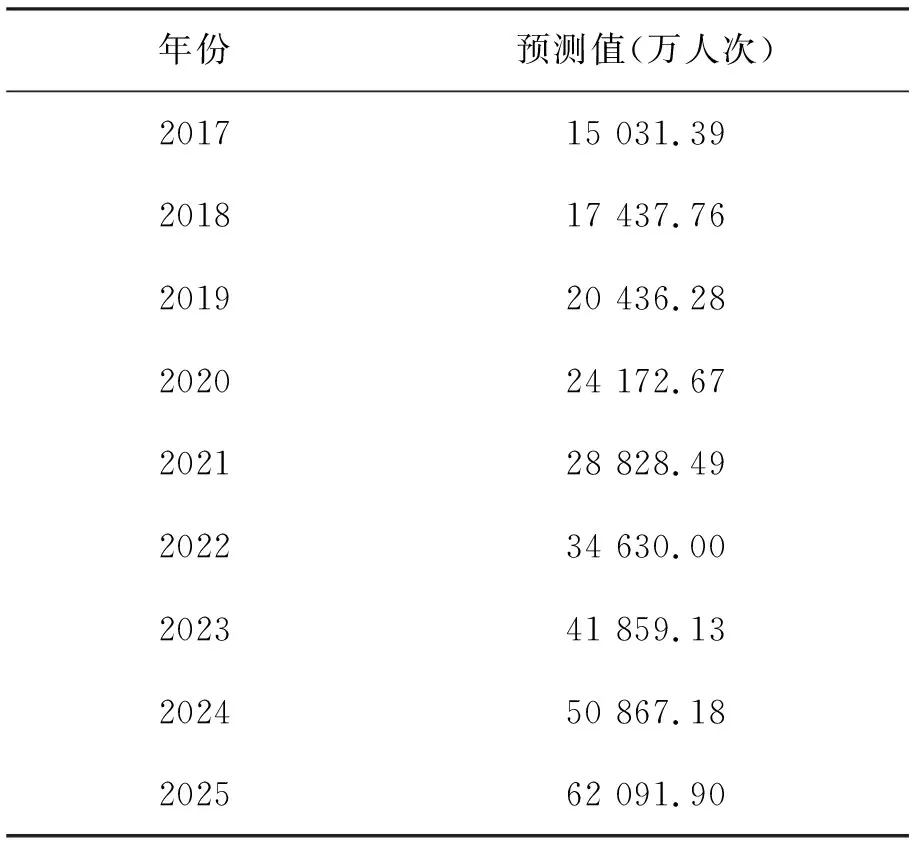
表6 2017—2025年中国居民出境游规模预测结果

四、结论

灰色GM(1，1)模型在处理具有指数增长趋势的原始数据方面预测精度很高，而对线性变化的原始数据预测效果不是很好；线性回归模型在处理线性变化的原始数据方面预测精度很高，而对具有指数增长趋势的非线性变化数据预测效果不佳。在原始数据既有一定的线性变化，又有一定的指数增长趋势的情况下，单独利用灰色GM(1，1)模型或线性回归模型进行预测，其预测效果都不是很好。因此，为实现中国出境旅游客流较高精度的预测，更好地捕捉变量间线性与非线性复合特征，鉴于线性回归和灰色理论模型存在的不足，本文在线性回归和灰色预测模型的基础上，系统推导出更加符合现场实际的灰色线性回归组合模型。通过实证对比分析显示，灰色线性回归组合模型的最小误差概率p为1，则该组合模型为1级精度模型，相对误差最小，为2.33%，且后验差比C最小，为0.021。可见，相比于其他两个单项预测模型，灰色线性回归组合模型的预测效果最优，具有较强的适用性，且该组合模型在面对随机性和波动性大的数据时，能有效弥补单一预测模型在拟合度和精度不足的缺点，挖掘变量间复杂的线性与非线性关系，具备较强的数据处理能力和较高的预测精度。在数据预测过程中，有利于综合两种单一模型中有用的信息，增强预测结果的精密化、准确性，更系统、更全面、更科学。

从灰色线性回归组合模型对中国2017—2025年出境旅游规模预测结果可见，未来几年中国出境旅游市场规模将以21%的平均增长速率继续扩大，至2025年中国出境旅游客流规模将达到6.2亿人次，出境旅游发展态势良好。可见，中国出境旅游市场潜力巨大，随着人们生活水平的提高，国民旅游需求的旺盛，未来出境旅游将成为中国旅游市场的一大热点。