50CrV钢激光填丝焊焊缝成形多元非线性回归模型

张川， 张福隆， 李跃峰， 刘双宇， 薄洪雨， 张宏， 李彦清

(1.长春理工大学 机电工程学院， 吉林 长春 130022； 2.长春一东离合器股份有限公司 吉林 长春130103)

0 引言

异种金属激光焊接始于20世纪70年代，目前已成为航空航天、船舶制造、汽车制造等领域重要的先进制造技术之一。异种金属材料焊接是解决结构件同时满足各方面性能要求和降低生产成本的有效途径，例如汽车离合器中的传动盘、从动盘结构件就是由高碳钢与低碳钢异种材料焊接而成的。用激光焊接高碳钢时，焊接接头会出现裂纹。激光填丝焊可以通过填丝来改变焊缝区的成分和组织，提高接头性能，并获得较小的焊缝热影响区[1-3]，从而解决高碳钢焊接存在裂纹的问题。但是，激光填丝焊可调参数较多，任意参数的调整都会对焊接质量和焊缝形貌产生影响[4]，而参数对焊缝形貌的影响是交互的。因此，研究工艺参数对焊缝形貌的影响具有重大意义。

响应面实验设计法能够很好地展现参数与响应之间的关系，且能对响应进行预测[5-6]， 1951年，数学家Box和Wilson首先提出该方法，随后被广泛应用于各类焊接优化设计[7]。孙硕等[8]基于响应面实验设计法建立了高氮钢激光-电弧复合焊接工艺参数与响应之间的多元非线性回归模型，并分析出工艺参数对响应的影响规律；王洪潇等[9]基于响应面实验设计法建立了不锈钢车体激光焊接工艺参数与预测响应值之间的数学模型，通过优化激光焊接工艺参数实现焊缝成形与接头强度的最佳组合；刘佳等[10]在对厚度为 0.8 mm与1.5 mm的SUS301L奥氏体不锈钢进行激光搭接焊接实验时采用响应面法，对激光焊接工艺参数进行优化分析，得到了最佳焊接条件；Torabi 等[11]在焊接AISI316L不锈钢时基于响应面实验设计法，以接头拉伸强度最大化为优化目标，建立了可用于精确预测响应的数学模型，获得的焊缝最大拉伸强度达到母材的96%；Kumar等[12]基于响应面实验设计法优化了激光焊接Ti-6Al-4V 合金的工艺参数，并获得了性能良好的焊接接头；Kiaee等[13]基于响应面实验设计法，优化了用钨极惰性气体保护焊方法焊接A516-Gr70碳钢的工艺参数，获得的焊接接头力学性能优良，满足了使用需求。

本文拟运用实验设计软件Design-Expert8.0进行响应面实验设计，并对实验数据进行处理和分析，建立焊缝形貌参数(熔深、熔宽、余高)与各工艺参数(激光功率、焊接速度、离焦量、送丝速度)的多元非线性回归数学模型。同时基于该模型分析各参数的交互作用对焊缝熔深、熔宽、余高的影响规律。

1 实验设备与方法

1.1 实验设备

激光填丝焊接系统如图1所示。实验采用由德国Trumpf公司生产的HL4006D型Nd：YAG 固体激光器和WF-007A多功能自动氩弧焊填丝机组成的旁轴送丝焊接系统。激光器最大输出功率4 kW，波长为1.06 μm,激光经220 mm聚焦镜后获得直径为0.6 mm的光斑。保护气体为氩气，焊接材料为150 mm×29 mm×6.8 mm 50CrV钢板，用砂纸打磨表面并用丙酮清洗。采用前送丝平板堆焊，焊丝材料为304奥氏体不锈钢，焊丝直径为0.6 mm.

1.2 确定实验因素及响应

激光填丝焊中影响焊缝形貌的参数众多，包括激光功率PL、焊接速度vw、送丝速度vf、离焦量D、保护气体流量L、送丝角度等，其中激光功率PL、焊接速度vW、送丝速度vf、离焦量D对焊缝形貌有显著影响。保护气体的主要作用是保护焊接熔池不被氧化，但其对焊缝形貌影响不大，因此焊接时选择氩气流量为15 L/min. 送丝角度的变化会影响焊丝的指向和伸出长度，实验中取送丝角度为60°. 焊缝的主要形貌主要通过熔深Yd、熔宽Yw、余高Yh等参量来评价，如图2所示。

1.3 确定工艺参数范围

为找到合理的参数范围，进行单变量实验，通过分析焊缝形貌，得到工艺参数范围。当激光功率低于2.9 kW时，焊缝熔深小，如图3(a)所示；当激光功率高于3.5 kW时焊缝熔深过大，焊缝有裂纹及气孔等缺陷，如图3(b)所示。当焊接速度低于1.0 m/min时，焊缝的熔深、熔宽过大，远远超过焊接需求，如图3(c)所示；当焊接速度大于1.4 m/min时，焊丝颤抖剧烈，造成焊缝弯曲，如图3(d)所示。当送丝速度低于4 m/min时焊缝成形较差，有缺陷，如图3(e)所示；当送丝速度大于6 m/min时会产生大的余高和小的熔深，如图3(f)所示。当离焦量大于5 mm时，为大熔滴过渡，焊缝成形不均匀，如图3(g)所示；当离焦量小于3 mm时出现熔深过大的现象，如图3(h)所示。

1.4 建立实验设计模型

采用4因素3水平和中心复合设计模型用于设计实验，实验因素水平编码及范围如表1所示。根据表1的因素水平编码运用Design-Expert响应面设计模块设计焊接实验，为避免系统误差以随机方式排列实验顺序。实验参数及响应如表2所示。

表1 工艺参数水平编码及范围

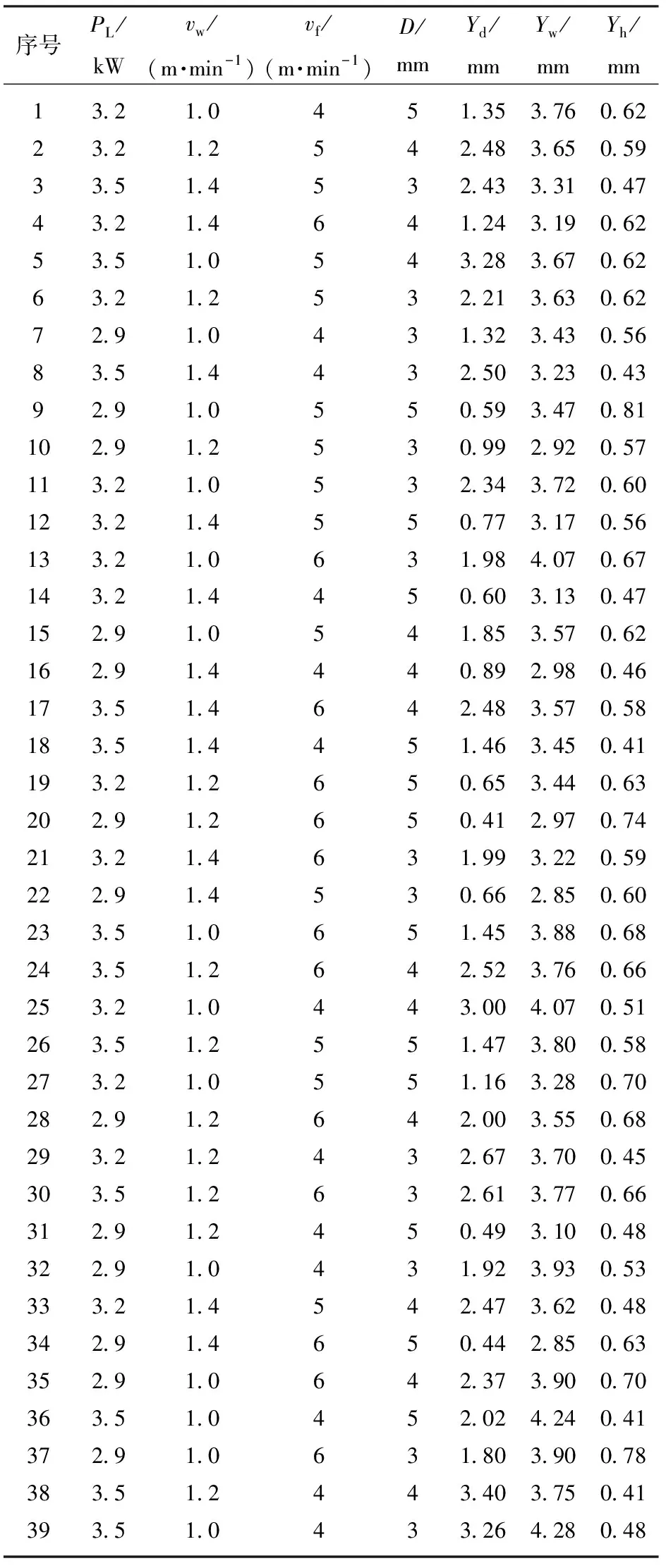
表2 实验参数及响应

2 建立数学模型

响应面法是数学和统计学的结合，主要用于分析几个独立变量影响一个或几个响应的问题。响应面法通常会给出工艺参数与响应之间的数学模型，通过对回归方程的分析优化工艺参数，用于预测响应并找到给出最佳响应的工艺参数[14-15]。当所有的独立变量在实验中可测、可控、连续时，则在忽略误差情况下，响应面可以表示为

y=(x1,x2,…,xN)，

(1)

式中:y为响应；x为独立变量；N为变量的数量。

数学建模就是找到1个合适的近似值来满足多个变量与响应面之间的方程关系，k次回归方程为

(2)

式中：a0为2次回归方程的常数项系数；aj为回归方程的1次项系数；aij为回归方程的交叉项系数；ajj为2次方程的平方项系数；ajk为k次项系数。

2.1 回归模型的选择

Design-Expert 8.0软件分析建模模块根据表2，运用最小二乘法计算出回归方程的各项系数并建立数学模型。参照熔深、熔宽、余高的多种回归模型的方差分析(ANOVA)和拟合度R2综合分析比较见表3～表8，以尽量选择高阶模型为设计准则，熔深的最优回归模型是2次方回归模型，熔宽最优回归模型是2FI(含有2因素交互作用)回归模型，余高的最优回归模型是线性回归模型。表中F值为F检验的统计量，用于衡量模型的显著性；而概率P>F为在相应F值下的概率值。F值越大，且概率P>F小于0.05时，说明结果越精确。

2.2 建立模型与方差检验

用方差分析的形式拟合响应面模型的结果，焊缝熔深、熔宽、余高的方差分析如表9～表11所示，表中3个模型的概率P>F值均小于0.05，表明模型是有意义的。每个模型的R2值、R2校正值、R2预测值差距较小且接近1，表明建立的回归模型精确。图4为焊缝熔深、熔宽、余高的正态概率残差图，图中残差越接近直线意味着误差分布越正常，回归模型拟合得越好。综上所述可知全部回归模型都是正确的。

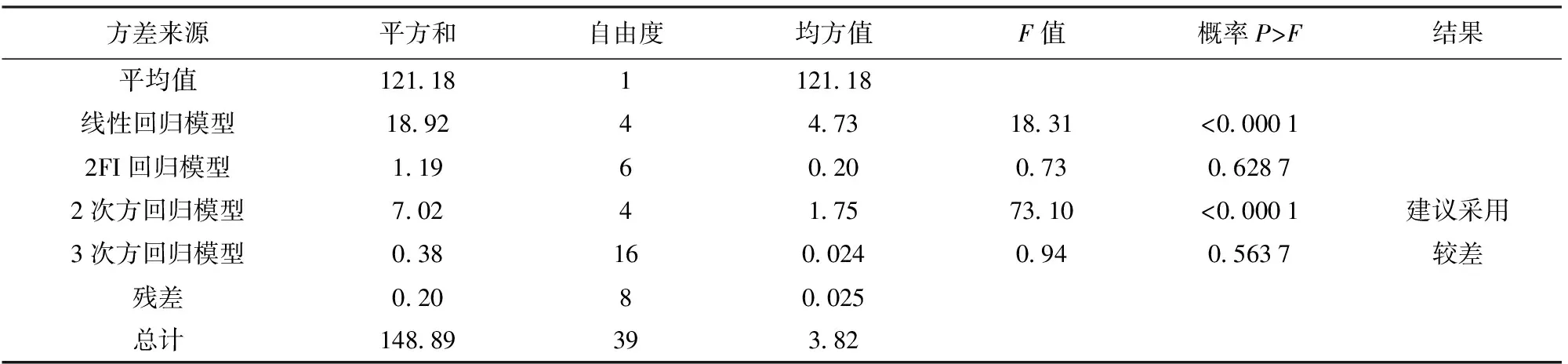
表3 焊缝熔深多种回归模型的方差分析比较

表4 焊缝熔深多种回归模型的R2综合分析

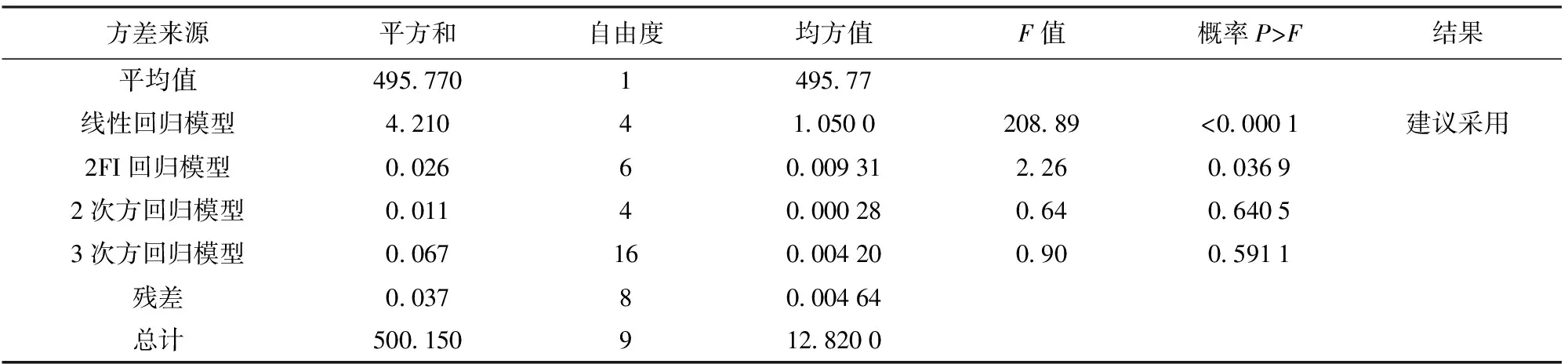
表5 焊缝熔宽多种回归模型的方差分析比较

表6 焊缝熔宽多种回归模型的R2综合分析

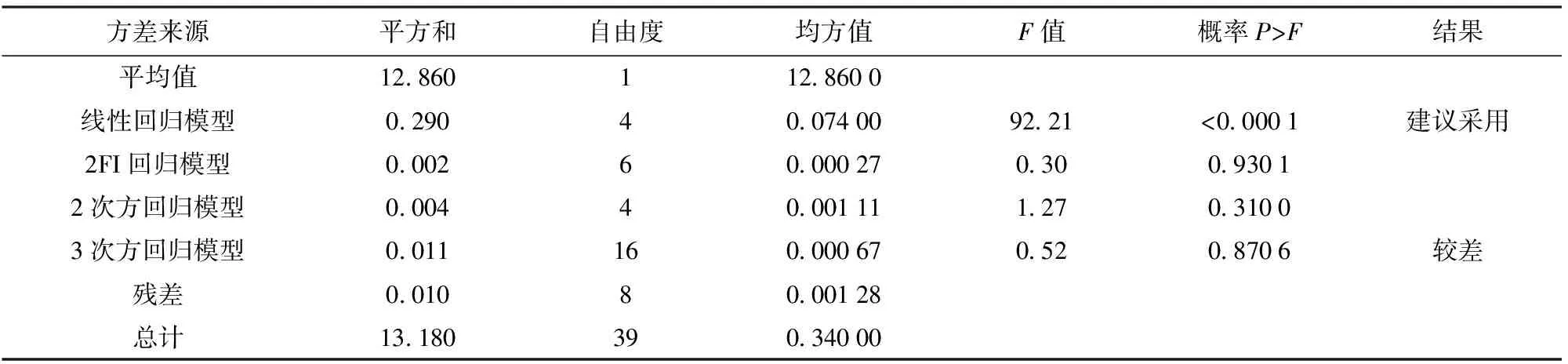
表7 焊缝余高多种回归模型的方差分析比较

表8 焊缝余高多种回归模型的R2综合分析

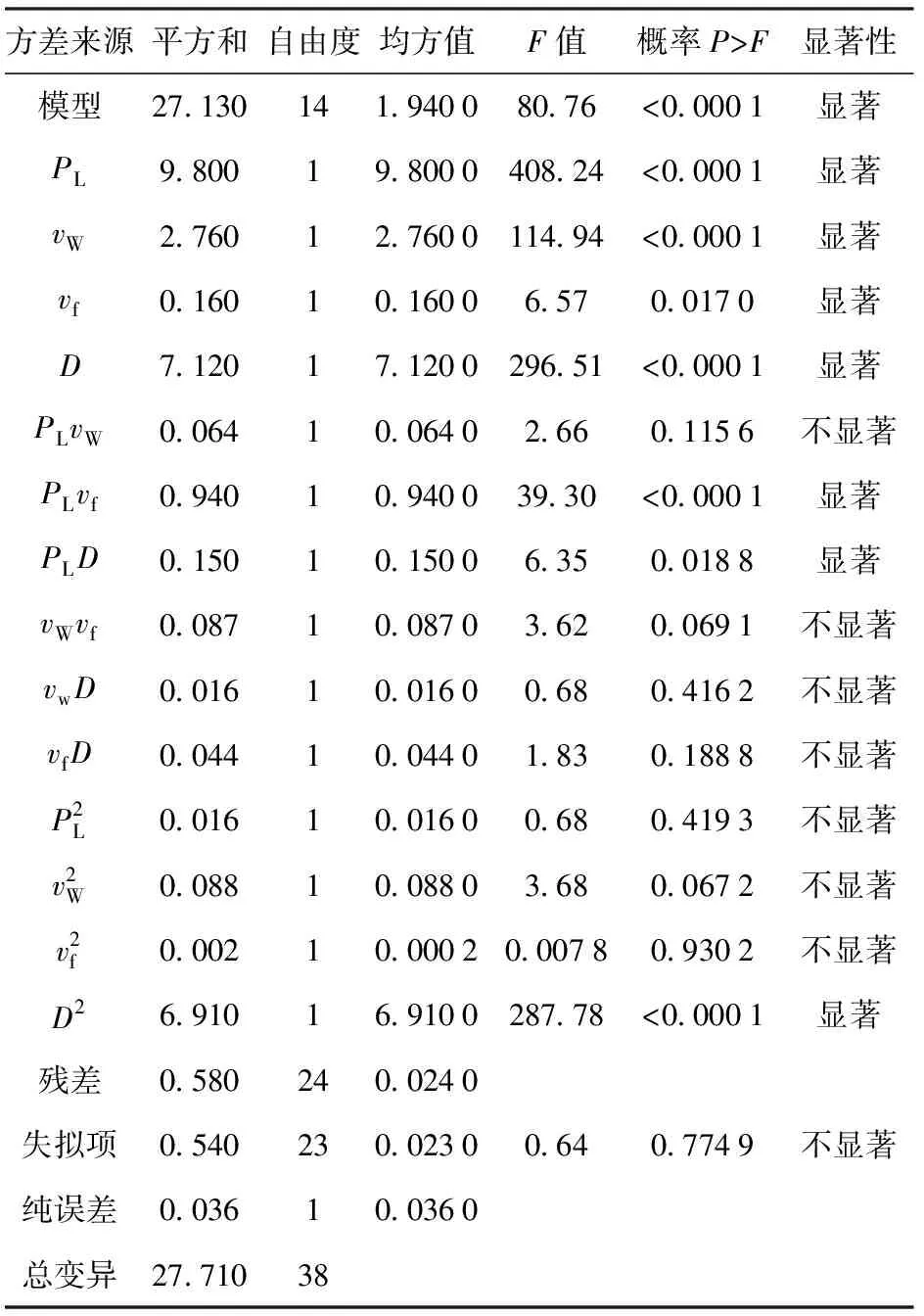
表9 焊缝熔深2次方回归模型方差分析

注：R2=0.979 2，R2校正值=0.967 1，R2预测值=0.930 6.

由于回归方程由Design-Expert 8.0软件自动生成，最终基于代码因素和实际因素的简化数学模型如(3)式～(8)式所示。

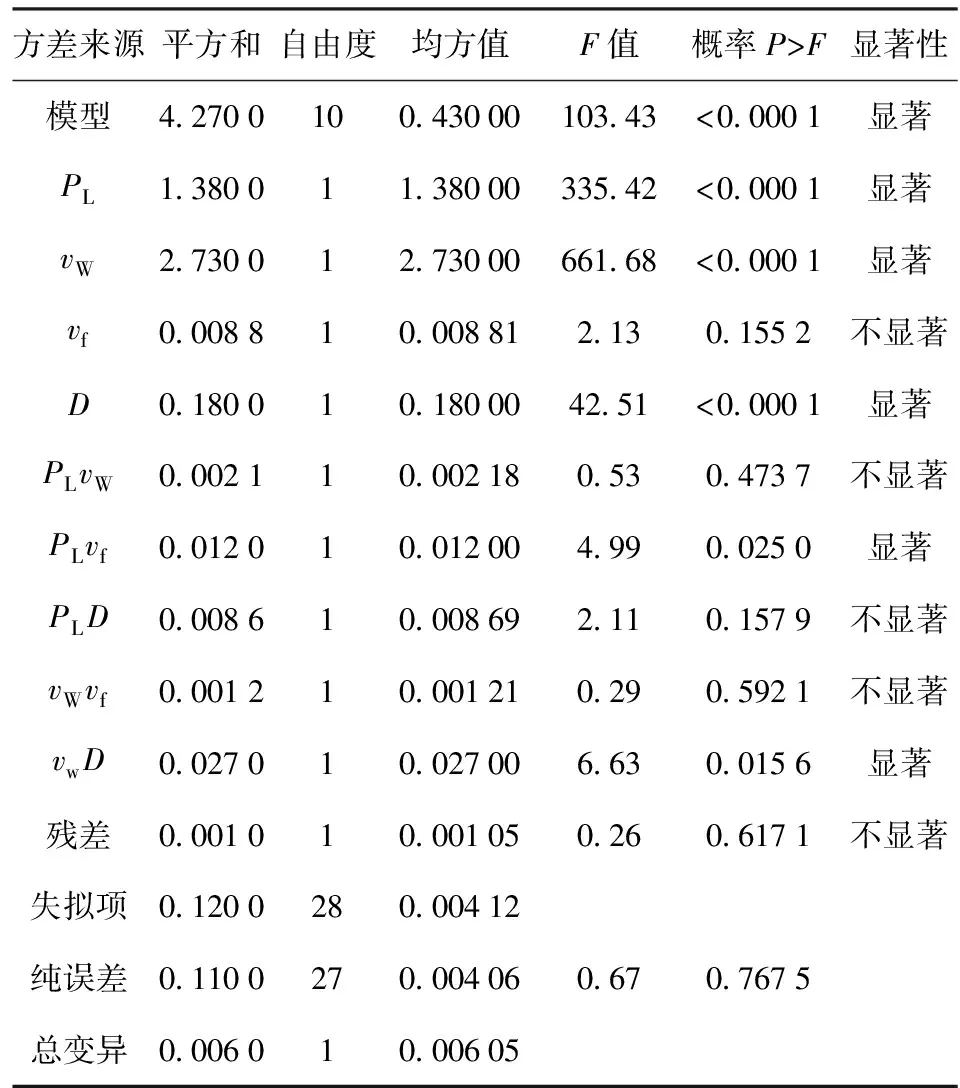
表10 焊缝熔宽2FI回归模型方差分析

注：R2=0.973 6，R2校正值=0.964 2，R2预测值=0.950 0.

表11 焊缝余高线性回归模型方差分析

注：R2=0.968 4，R2校正值=0.952 3，R2预测值=0.942 5.

1)基于因素代码形式的回归模型：

焊缝熔深

(3)

焊缝熔宽

Yw=3.54+0.25PL-0.33vw-0.019vf-0.084D+0.012PLvw-0.027PLvf+0.024PLD+0.008 582vwvf+0.039vwD-0.007 92vfD；

(4)

焊缝余高

Yh=0.57-0.018PL-0.049vw+0.089vf+0.014D.

(5)

2)基于实际因素值的回归模型：

焊缝熔深

Yd=-34.572 40+9.327 59PL-1.264 24vw+2.251 09vf+8.010 79D-0.787 05PLvf-0.334 66PLD-0.925 47D2;

(6)

焊缝熔宽

Yw=4.720 24+0.709 76PL-3.285 64vw-0.533 78D-0.089 385PLvf+0.197 3vwD-0.007 93vfD;

(7)

焊缝余高

Yh=0.556 18-0.061 519PL-0.243 26vw+0.089 246vf+0.013 510D.

(8)

3 实验结果与分析

3.1 工艺参数交互作用对焊缝熔深的影响

图5为工艺参数交互作用对焊缝熔深影响的三维响应面图，其中底面上的曲线为响应面投影，即响应保持不变时，两因素之间的相互关系。分析图5可知，高的激光功率能产生大的熔深，低的焊接速度也能产生大的熔深，激光功率越大，焊接速度越小、熔深越大，如图5(a)所示。从图5(b)可以看出，低送丝速度和高激光功率获得的熔深大；从图5(d)可以看出，低焊接速度和低送丝速度有利于产生大的熔深；从图5(c)可以看出，熔深随着离焦量先增大、后减小，中间位置的离焦量和高激光功率产生的熔深较大；图5(e)和图5(f)有相同的规律，靠近中间位置的离焦量产生的熔深较大，但是图5(e)中越小的焊接速度产生的熔深越大，图5(f)中送丝速度的变化对熔深的影响不明显。

3.2 工艺参数交互作用对焊缝熔宽的影响

结合表10选择对熔宽影响显著的工艺参数进行分析，从得到的三维响应面图(见图6)可看出，工艺参数交互作用对焊缝熔宽的影响规律大致相同。图6(a)为激光功率与送丝速度交互作用对熔宽的影响。从图6(a)可以看出，高送丝速度和低激光功率获得的熔宽小，但是随着送丝速度的增大，焊缝余高也增大，因此要找到焊缝熔宽最小化和余高最小化的平衡点。从图6(b)可以看出，随着焊接速度和离焦量的不断增大，获得的熔宽逐渐减小。

4 实验优化与验证

焊缝应尽可能深宽比大，因为焊缝熔宽越窄，热影响区就越小，对母材的影响越小，焊缝区会更多地体现母材的力学性能[6,16]。根据Martinez-conesa等[17]和Al-Mukhtar等[18]的研究，少量的余高有助于增强焊缝力学性能，而过高的焊缝余高会造成应力集中，减少焊缝使用寿命[17]。因此在满足特定的焊缝熔深基础上，熔宽和余高应尽可能小作为优化准则。为下一步焊接实验选择合理参数，本优化实验焊缝熔深要求控制在2.0 mm,允许少量偏差。详细优化条件如表12所示。

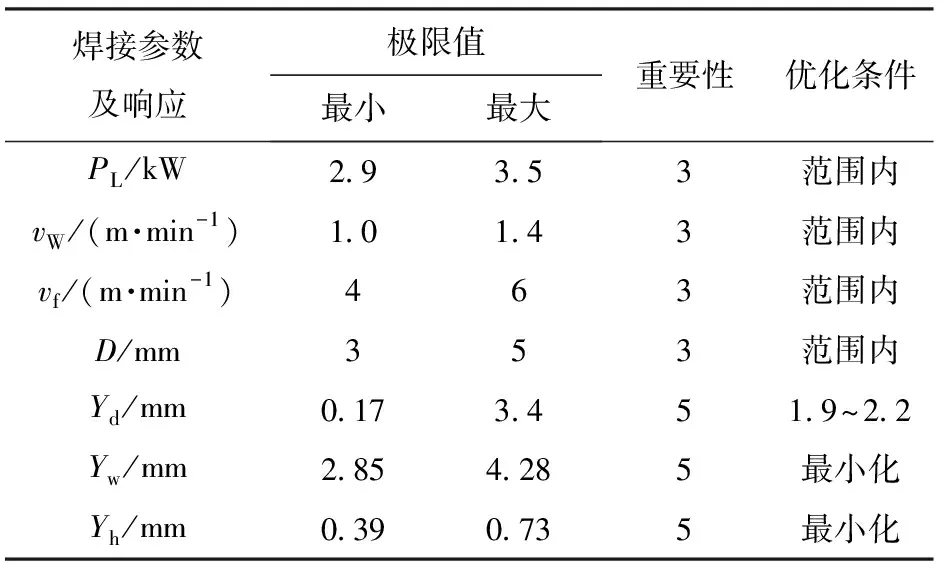
表12 实验优化条件

表13是Design-expert 8.0软件根据表12给出的优化条件得到的焊接实验最优工艺参数和预测结果，表14是最优工艺参数下的验证结果。根据验证结果可知，当激光功率为3.17～3.33 kW、焊接速度为1.30～1.40 m/min、送丝速度为4.00～4.23 m/min、离焦量为3.1～4.5 mm时，可获得熔深1.97～2.00 mm、熔宽3.20～3.33 mm、余高0.39～0.44 mm的焊缝形貌良好的接头。图7为验证实验部分焊缝截面，焊缝熔深在2.0 mm附近。图8为实际值与预测值对比图，从图8中可以看出实验结果与优化结果相吻合。

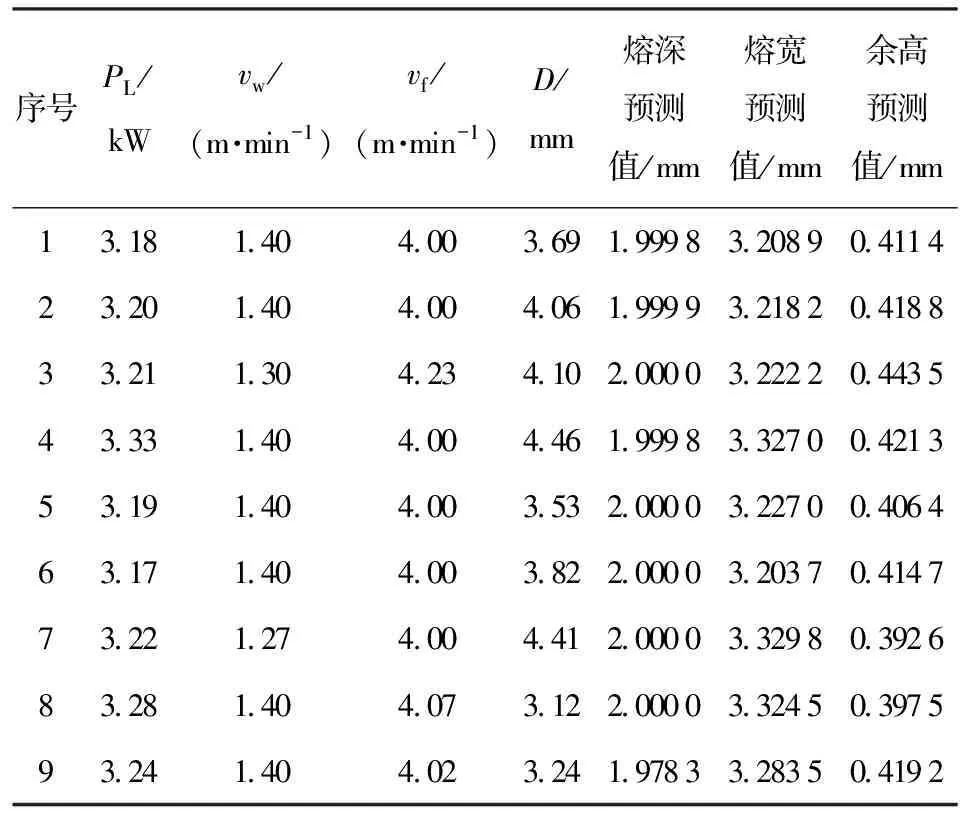
表13 实验最优工艺参数及预测结果

5 结论

本文对6.8 mm厚50CrV 钢进行了Nd:YAG激光填丝平板堆焊实验研究。基于Design-Expert8.0软件，分析了工艺参数及交互作用对焊缝几何尺寸的影响规律，建立了焊接过程的数学模型，以特定需求的熔深、最小化的熔宽及余高为优化目标，并应用于验证实验。具体结论如下：

1)50CrV钢激光填丝平板堆焊的焊接工艺参数对熔深、熔宽和余高影响的多元非线性回归方程预测值与验证实验实测值相吻合，回归方程能用于后续实验。

2)激光功率、焊接速度、送丝速度、离焦量主效应对焊缝特征影响最大；激光功率与送丝速度和激光功率与离焦量的交互作用对熔深影响最大；送丝速度与激光功率、焊接速度与离焦量的交互作用对熔宽的影响最大。

3)当激光功率为3.17～3.33 kW、焊接速度为1.30～1.40 m/min、送丝速度为4.0～4.23 m/min、离焦量为3.1～4.5 mm时，可获得熔深为1.97～2.0 mm、熔宽和余高最小化的焊缝接头。