基于灰色综合评估法的高职院校专业群评价

朱 炼 ，夏芳莉 ，丁 浩 ，汪飞燕

（1.安徽工商职业学院 应用工程学院，安徽 合肥 231131；2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001）

0 引言

在高职院校的专业建设中，若干个相近专业组成一个专业群.专业群的建设有利于相近专业的师资资源、实验实训资源和课程资源等的高效利用和共享.当前，国内学者主要从高职院校专业群的课程体系构建、专业群与产业群的协调发展、建设路径等方面对高职院校专业群进行研究.例如：文献[1,2]以具体的专业群为例研究了高职院校专业群课程体系的构建方法；文献[3-5]研究了高职院校专业群与产业群的协调发展的相关问题；文献[6,7]提出了高职院校专业群的建设具体路径.但是，国内学者对高职院校专业群评价的研究较少.王传斌等[8]以连云港师范高等专科学校“港口涉外商务专业群”为例，研究了高职院校专业群评价指标体系和权重，但是该研究以定性分析为主，没有运用相关模型进行定量评价.本研究运用灰色综合评估法对高职院校专业群进行定量评价，具有一定的实际意义.

1 高职院校专业群评价的指标体系及权重

根据教育部的高职院校人才培养水平评估方案并结合高职院校专业群建设的实际情况，将高职院校专业群评价指标分为一级指标和二级指标，包括5个一级指标和12个二级指标.运用Delphi法，得到各个指标的权重.专业群评价的指标体系及权重如表1所示.

2 灰色综合评估法

灰色综合评估法是以建立在灰模型上的白化权函数来评估对象的灰类等级.

设评估对象为i（i=1，2，…，n）；评估指标为j（j=1，2，…，m）；dij表示第i个评估对象的第j个指标值，根据专业群情况，将评估灰类设置为优、中、差3个等级.

白化权函数[9，10]中的高类白化权函数为：

表1 高职院校专业群评价的指标体系及权重

式中：H为高类下限，用评估对象指标值的平均值加标准差表示；Z为中类中限，用评估对象指标值的平均值表示.

白化权函数[9，10]中的中类白化权函数为：

式中：L为低类上限，用评估对象指标值的平均值减标准差表示.

白化权函数[9，10]中的低类白化权函数为：

式中：p为子系统k的指标数；f1，f2，f3分别为高、中、低类白化权函数值，该值与权重的乘积和称为综合权系数.

设子系统k的权重为Rk，则系统的综合权系数矩阵为：

式中：s为系统所包含的子系统数.子系统综合权系数与权重的乘积和称为系统综合权系数.

系统或子系统各评估指标所属评估灰类的等级为综合权系数矩阵或权系数矩阵中各行最大值对应的灰类等级.

3 实证研究

安徽工商职业学院是安徽省级示范院校.安徽工商职业学院工科类专业主要组成机电工程专业群（G）、智能工程专业群（U）和汽车工程专业群（V）等三大专业群.我们邀请专家依据学校三大专业群的基础数据对三大专业群评价指标体系中的12项二级指标进行评分，在评分栏中每一项二级指标的满分为100分.再将多位专家对每一项二级指标的评分结果的平均分作为该项二级指标的得分.根据得分构造样本矩阵，并计算相关统计值，如表2所示.

根据表2数据，由（1）～（3）式计算出G、U、V三大专业群二级指标的高类白化权函数值、中类白化权函数值和低类白化权函数值，如图1所示.

根据三大专业群二级指标的白化权函数值，对二级指标进行灰色评估，得到三大专业群二级指标灰类等级，如表3所示.

根据二级指标的权重值，由（4）式得到三大专业群一级指标的等级，如表4所示.

根据一级指标的权重值，由（5）式得到三大专业群的评价等级，如表5所示.

表2 样本矩阵及统计值

表3 三大专业群二级指标灰类等级

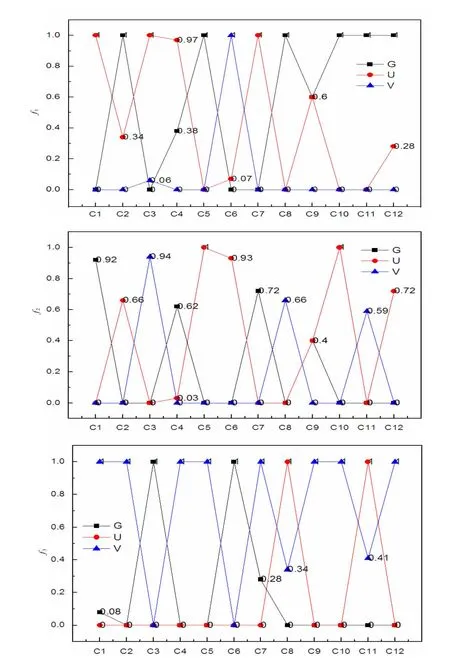
图1 三大专业群二级指标的白化权函数值

表4 三大专业群一级指标的等级

表5 三大专业群的评价等级

4 结语

运用灰色综合评估法既可以得到高职院校专业群总体评价的灰类等级，又可以得到每一级指标的灰类等级，而传统的评估法只能得到总体评价值的大小，不能直接得到优、中、差等次.获得每一级指标的优、中、差等次，可以为高职院校有针对性地进行专业群建设提供参考.