RSS测距模式下水声传感器网络半正定松弛定位算法*

王 辉， 李有明， 毛雁明

(1.宁波大学 信息科学与工程学院，浙江 宁波 315211； 2.宁德师范学院 计算机系，福建 宁德 352100)

0 引 言

近年来，关于水声传感器网络(underwater acoustic sensor network,UASN)的研究受到各国政府和研究机构的高度重视，且在军事和民用方面得到广泛应用，对于大部分的应用而言，水下定位是关键环节之一[1]。然而，由于水声环境的复杂性，如传输时延大、噪声高、载波频率低等特点，与陆地上相比，节点定位精度具有更高的要求。这些因素给UASN中传感器节点定位带来了巨大的挑战。

常见的UASN节点定位算法可分为基于测距和非测距的算法两类[2]，其中基于测距的算法主要依赖于节点间的距离信息，如到达时间(time of arrival,TOA)、到达时间差(time difference of arrival,TDOA)、到达角度(angle of arrival,AOA)以及接收信号强度指示(received signal strength indication,RSSI)。TOA广泛应用于UASN的测距[3]，但两节点间的精确同步具有挑战性。TDOA可使用不同的传输介质(如无线电波和声波)或采用参考节点来估计距离，但无线电波不适合水下环境，且声波的水下速度具有不可预测性[2]。AOA依赖于直线视距声线传输路径，其在地面无线电波中可能存在，而水声信道中存在典型的多径分量，这会导致AOA测量时出现较大的误差[4]。基于接收信号强度(received signal strength,RSS)的水下定位方案作为衡量距离的另一种替代方案，由于多径传播和声线传输损失(transmission loss,TL)现象使得精确测距难以实现[5]。然而，当水深达到一定程度后，水声信道会表现出良好的传输特性，可建立声线传输损耗模型，因此，在这种情况下，基于RSS的定位方案最适合。

对于描述水声信道的声线传输损耗特征，Urick传播模型[5]能够衍生出一些统计特性。当然，还有其他水声声线传输损耗建模方法，如Lambert W函数[6]。目前，UASN中基于RSS的定位算法的文献相对较少，如文献[6]利用Lambert W函数建立水声传播损耗模型，并结合三边测量定位算法计算未知节点的坐标；文献[7]提出一种基于TOA和RSS的混合定位算法，其中基于RSS的测量作为已知信息；文献[8]采用地面声波传播模型来研究基于RSS的水下定位。由于水声环境的特殊性，在基于RSS测量系统中，阴影是不可忽略的因素。上述文献仅简单假设任意两个不同位置的阴影相互独立，不具有相关性。为此，本文以空间阴影相关性为背景，在上述工作的基础上，推导和分析水声信号传播模型，提出一种基于RSS的定位的优化求解方案。

1 基于接收信号的定位算法

1.1 传播损耗模型

根据水声传输损耗的表现形式和原因，将水声传输损耗分为扩散损耗和衰减损耗。扩散损耗表示波前展开而产生的声能扩散，主要包括球面和柱面两种形式。衰减损耗由介质吸收、多径传播、散射和衍射组成，其衰减参数与介质(盐度，酸度，压力和温度)和环境(气泡，沉积物吸收，表面反射和散射)有关[5]。以频率f为中心的声窄带信号经过距离d(d>0)传播的传播损失φTL可由Urick传播模型

φTL(f,d)=10βlgd+α(f)d+ξ(f,d)

(1)

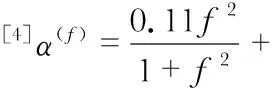
1.2 系统模型

(2)

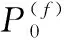
(3)

式中δdB为常数值，值的大小取决于传播环境；若以dB为单位，通常为4～12 dB之间；pij为第i条与第j条链路之间的相关系数。与大多数假设pij为零不同，一对节点之间的相关性取决于两者的相对角度和距离[14]研究表明，相关系数的值通常取在0.2～0.8之间。

1.3 最大似然求解

克拉美罗下界(Cramer-Rao lower bound,CRLB)定义了任何无偏估计器性能的下限。当测量次数趋于无穷大时，最大似然(maximum likelihood,ML)估计可以渐近地达到CRLB。为方便起见，本文选择d0=1。若路径损耗指数β和吸收系数α(f)为已知，式(2)估计问题可转换为

(4)

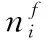
2 半正定松弛定位算法

针对上述问题，本节提出了一种基于半正定松弛(semi-definite relaxation,SDR)的求解算法。首先通过泰勒级数展开，将原最大似然估计问题作为代价函数转换成非线性最小二乘(nonlinear least squares,NLS)问题。重新排列式(2)，并两边除以10β得到

(5)

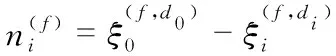
(6)

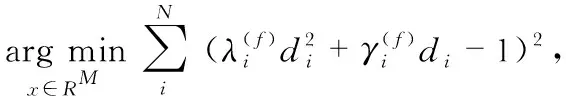
(7)

同时，引入di=‖x-si‖2>0和松弛变量ti≥0，本文将优化问题式(7)转换成

(8)

进一步将式(8)的约束项转换为

[D]i,i=tr[XSi]

(9)

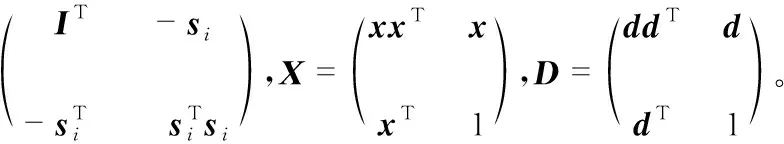
最后，最小化问题(9)可转换为半正定优化问题，即

(10)

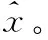
3 仿真分析

通过仿真验证空间阴影相关对基于RSS的定位精度的影响，并比较基于SDR算法，ML定位算法和线性最小二乘算法(linear least-squares,LLS)的3种定位方案的性能，验证本文所提出算法的有效性。在100 m×100 m的矩形区域内，采用蒙特卡罗(Monte Carlo)法进行了1 000次仿真测试，其中每次测试随机部署6个锚节点和1个未知节点。另外，通过式(2)获得RSS测量值，其中水声信号传输频率f为9 kHz，路径损耗指数β和参考功率P0分别设置为4,-40 dB。对于相关系数pij和标准差δdB的取值，则在分组测试时分别设置。式(3)描述的协方差矩阵Q是一个对称的半正定矩阵，通过Cholesky分解，Q可表示为[9]Q=BBT,B为下三角矩阵。若n=[n1,n2,…,nN]是式(2)中RSS测量时各条链路之间相关噪声，且服从均值为零，协方差为Q的高斯随机变量。那么n=Bw,w为一个向量，服从均值为零，方差为1的正态分布的独立随机变量。

1)假定水声环境中任意2个节点所处位置的阴影相互独立，且不具有相关性，此时，设置pij=0，δdB=4 dB。图1采用累积分布函数(cumulative distribution function,CDF)曲线对比了3种算法的估计定位误差。与其他估计算法相比，最大似然定位算法的精度最高，其90 %的定位误差小于23 m，具有良好的性能，主要是因为其初始化值取为真实解。当然，本文所提出的半定松弛定位算法同样具有良好精度，其性能非常接近最大似然。而最小二乘算法在3种定位算法中的表现最差，其90 %的定位误差小于25 m。

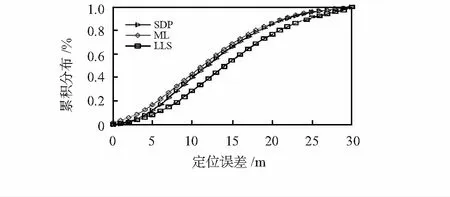
图1 定位误差的CDF比较(δdB=4 dB，p=0)

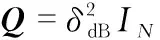
从图2可以看出，与图1中的不相关的情况相比，阴影相关性的最大似然在90 %的CDF处定位误差减少到12 m，整体性能有所提升。同样，本文提出的半定松弛定位算法也表现出了良好的精度，其性能仍非常接近最大似然。

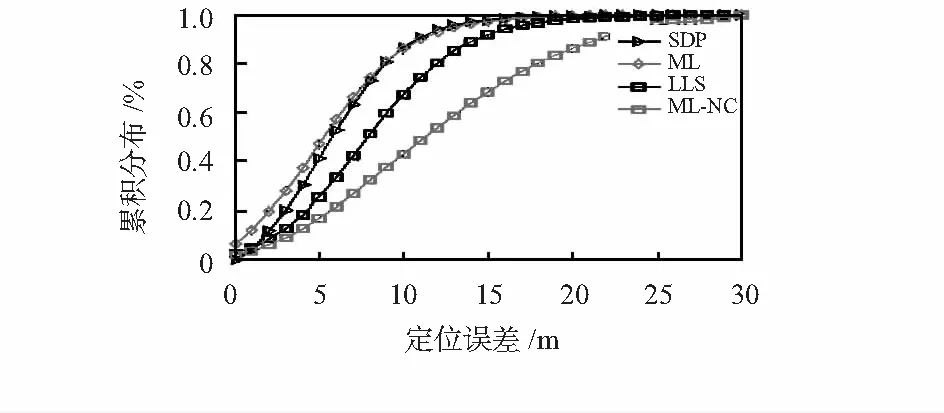
图2 定位误差的CDF比较(δdB=4 dB,p=0.8)

3)比较了所考虑的估计量的平均运行时间。本文考虑与图2相同的网络配置，阴影的标准差为4 dB，相关系数为0.8。可知，LLS具有最快的运行时间[4](0.28 ms)，因为估计器需要简单的计算，所有这些都在一次迭代中完成。ML(16.54 ms)和ML-NC(15.13 ms)运行速度比SDP(42.16 ms)估计量快。然而，应该注意的是，ML和ML-NC初始值为真值，随着求解器在一些迭代后收敛，明显减少了运行时间[5]。ML需要更多的迭代次数，且运行速度比ML-NC高，主要是ML成本函数复杂度高的原因。由此可知，以上3种算法存在各自的问题，不适合推广，而本文提出的SDR定位算法虽然运行时间较长，但在可接受范围内，最重要的其表现出了良好适应性和精度。

4)考察变量δ对定位误差均方差根误差(root mean square error,RMSE)的影响。图3描述了相关系数p设定为0.8，阴影的标准差δdB为1～6 dB时，三种定位算法表现出来的RMSE的变化曲线。通过对所有源节点位置和随机噪声实现进行平均来计算每个定位算法的RMSE。由图3可知，ML与ML-NC之间的差异随着阴影标准差δdB的增大而增大，因此，在测量中考虑重度阴影的关系更有利。与此同时，本文提出的半正定松弛定位算法表现出很好的性能，与最大似然性能非常接近。

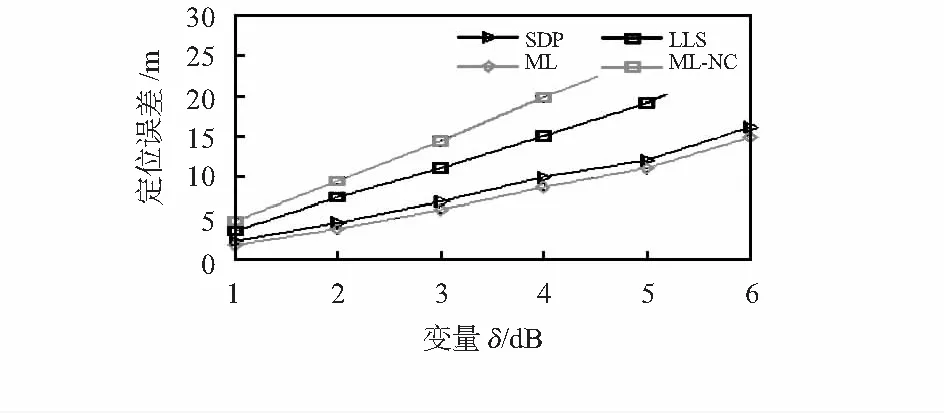
图3 RMSE随δ的变化关系(p=0.8)

4 结 论

本文所提出算法的性能非常接近最大似然估计的精度，且在不相关或相关的阴影环境下均表现出较强的适应性和较高的精度，因而更适合推广。