柔索牵引式机器人的姿态自适应调节控制优化*

陆兴华, 叶铭铭, 陈俊祥, 吴宏裕

(广东工业大学 华立学院，广东 广州 511325)

0 引 言

采用智能机器人进行柔索牵引作业,能有效提高柔索牵引作业的智能性,改善牵引和搬运作业的效率。在柔索牵引机器人的设计中,进行机器人的末端位姿的跟踪测量和参数调节是关键,根据柔索牵引机器人几何参数得到机器人末端位姿,获得的连杆模型参数能及时反馈给柔索牵引机器人,实现参数修正,提高机器人的控制稳定性和输出行为指向性。因此,研究柔索牵引机器人的末端位姿控制方法具有重要意义[1]。

目前柔索牵引机器人运动学末端位姿控制的方法主要有圆周点法、模糊比例—积分—微分(proportional-integral-differiential,PID)控制方法、运动学回路法和反演积分控制方法等[2,3]。前三种是将柔索牵引机器人的关节轴线抽象成一条空间中的直线,利用关节轴线间的几何关系求出机器人的几何运动参数,采用空间动力学模型进行机器人的稳态位姿调节,完成柔索牵引机器人的控制。后者采样反演控制律进行柔索牵引机器人的位姿测量和模糊控制,结合自适应控制律进行机器人的位姿参数调节和优化控制,提高跟踪性能,文献[4]提出一种基于动态跟踪测量的柔索牵引机器人末端位姿优化控制方法,根据柔索牵引机器人几何参数得到柔索牵引机器人末端位姿,采用改进扩展卡尔曼滤波方法进行位姿参量融合,提高控制稳定性,但该方法的抗干扰能力不强；文献[5]提出一种基于反演稳态误差补偿的柔索牵引式机器人扰动控制方法,实现大范围的高精度定位和姿态调节,采用时滞跟踪补偿模型构建柔索牵引式机器人控制的约束参量模型,提高机器人控制的人工智能性,但该方法在受到强扰动下的控制稳定性不好[6]。

针对上述问题,本文提出一种基于多传感器参量融合的机器人姿态自适应调节方法。设计柔索牵引式机器人的7自由度运动学模型,通过仿真实验进行性能测试,表明了本文方法在提高机器人的姿态控制稳定性方面的优越性能。

1 机器人的运动学模型与力学参量分析

1.1 柔索牵引式机器人的运动学模型

为了实现对柔索牵引作业智能机器人的稳定控制,构建柔索牵引作业智能机器人的惯性姿态融合空间运动学模型,需要进行柔索牵引作业智能机器人的7自由度运动空间规划,设计柔索牵引式机器人的7个旋转自由度运动模型,采用末端位姿估计器进行柔索牵引式机器人的姿态特征传感采集和控制约束参量分析[7],设计柔索牵引式机器人的7自由度运动学模型,如图1所示。

图1 柔索牵引式机器人的运动空间规划模型

以图1所示机器人的运动空间规划模型为研究对象,采用多传感器融合跟踪识别方法进行柔索牵引作业和位姿参量调节[8],传感器分别为加速度传感器、磁力传感器和转向传感器等,在多媒体视觉模型下进行柔索牵引作业动态模拟和智能控制,在柔索牵引式机器人6个自由度中采集机器人的定姿参数,得到柔索牵引式机器人的运动学分布的正则方程为

xL3=l1sinθ1+l2sin(θ1-θ2)+α3sin(θ1-θ2+θ3)-α0

(1)

xR3=α6-l5sinθ6+l4sin(θ5-θ6)-

α3sin(θ4-θ5+θ6)

(2)

(3)

对柔索牵引式机器人机构的运动学、动力学方程求解,可计算出mL3和mR3。柔索牵引式机器人的末端位姿构件的运动规律,得到柔索牵引式机器人的载荷输出为

(4)

式中Ii为柔索牵引式机器人质心转动惯量。结合机器人的力觉交互特征量,构建Lagrange动力学方程为

(5)

运用封闭矢量法进行机器人的运动学规划,采用动态运动基元学习方法进行机器人的末端姿态力学参量调节和自适应控制[9]。

1.2 机器人的控制参量分析

在构建柔索牵引式机器人的运动学模型的基础上,采用动态运动基元学习方法进行机器人的末端姿态力学参量调节和自适应控制[10],得机器人第i个组件的柔性力矩为

(6)

假设柔索牵引式机器人在运动中具有较大的速度和加速度,在移动惯性力矩的作用下,构建面向二自由度时滞系统的机器人机构控制函数为

S={(k,n),0≤k≤K,0≤n≤N}

(7)

结合柔性驱动分析方法,构建柔索牵引式机器人的电枢回路模型为

(8)

根据构建的柔索牵引式机器人的弹性流体动压模型,采用多传感器融合跟踪方法进行柔索牵引式机器人的位姿信息采集和融合滤波分析[11],封闭矢量模型描述为

(9)

式中t1

2 机器人姿态自适应调节控制优化

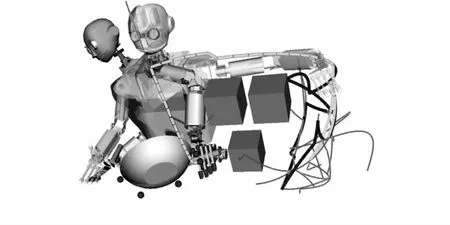
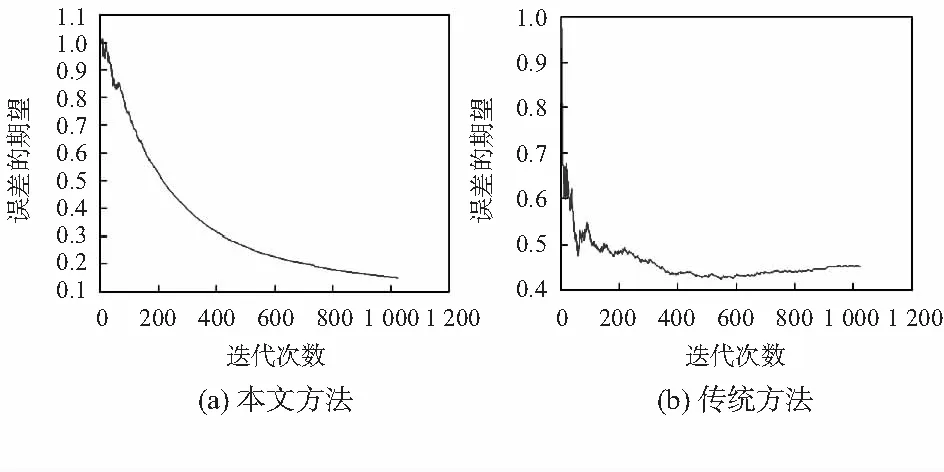
2.1 机器人姿态惯性参量调节和误差补偿

在设计柔索牵引式机器人的7自由度运动学模型,采用动态运动基元学习方法进行机器人的末端姿态力学参量调节和自适应控制的基础上,进行控制算法的优化设计,本文提出一种基于多传感器参量融合的机器人姿态自适应调节方法。建立机器人的移动平台和驱动单元进行的机器人姿态惯性参量调节,得到机器人的惯性力学场分布描述为

ZN=g·XN+WN

(10)

式中ZN=[z1,z2,…,zN]H为末端位姿估计动力参数,XN=[x1,x2,…,xN]H为刚体间所有理想约束力,WN=[w1,w2,…,wN]H为机器人的全局运动干涉矢量。从k-1～k时刻k时刻进行柔索牵引机器人传感信息融合跟踪识别,采用稳态误差跟踪识别方法,得出振动响应的控制误差为ex=x-xd,eθ=θ-θd,此时拉格朗日乘子作为未知变量,得到柔索牵引式机器人在零阶模态下阻尼控制方程为

(11)

式中X=[θ,x,,分别为约束方程对应的拉格朗日传递函数,dx(t),dθ(t)为机器人各连杆之间的载荷势能函数。

分析材料机械构件的载荷、屈服强度和应力强度之间的关系,得到柔索牵引式机器人机械性能传导方程为

(12)

据上述参数融合结果,构建柔索牵引式机器人的弹性流体动压模型,实现机器人姿态惯性参量调节和误差补偿。

2.2 柔索牵引式机器人姿态自适应调节控制律优化

采用模糊控制和双目视觉动态跟踪方法实现柔索牵引式机器人的优化控制设计,采用末端效应逆运动学分解方法对柔索牵引式机器人进行自主控制,得到机器人控制的位姿扩展运动学方程为pe=f(θ),建立机器人的移动平台和驱动单元进行的机器人姿态惯性参量输出的时滞跟踪补偿方程

(13)

(14)

采用柔性驱动机构运动学和动力学交互控制方法进行组织结构的演变力学控制,结合机器人末端位姿调节算法进行机器人的姿态跟踪识别,由此实现机器人姿态自适应调节控制。

3 仿真实验与结果分析

为了验证本文的算法在实现柔索牵机器人的末端位姿自适应调节和智能控制中的应用性能,进行仿真实验,搭建硬件平台,采用三轴电子罗盘LSM303DLH进行柔索牵引式机器人的姿态传感数据采集,控制算法采用MATLAB 7设计,设计机器人的末端姿态参数采集的周期为0.12 s,姿态传感信息采集的样本值为2 000,机器人的姿态初始调节误差为0.02,其他关键参数设定为：惯性力矩Mp=1.6×104kg,质量mr=1.13×104kg,转动惯量R=2.05 m。进行机器人控制的姿态自适应调节仿真,得到机器人的姿态控制有限元分析仿真结果如图2所示。

图2 机器人的姿态控制有限元分析仿真结果

以图2的柔索牵引式机器人有限元结构为研究对象,进行机器人的位姿动态跟踪测量和末端位姿调节,得到位姿参数控制输出结果如图3所示。

图3 机器人的姿态自适应调节控制输出

分析图3得知,采用本文方法进行机器人的姿态自适应调节控制,能有效实现参数修正及补偿,得到最优的姿态参量,柔索牵引机器人末端位姿调节能力较好。为了对比性能,采用不同方法进行机器人姿态自适应调节控制,得到控制学习曲线对比如图4所示。

图4 姿态控制学习性能对比

对比图4分析得知,本文方法进行柔索牵引机器人末端位姿调节控制的学习性能较好,收敛性较好,输出姿态参量的误差期望较低,机器人姿态自适应调节的鲁棒性和抗扰动性得到大幅提升。

4 结 论

采用该方法进行机器人姿态自适应调节控制的输出稳定性较好,末端姿态调整的误差为较低,提高了机器人的抗扰动能力,输出位姿的准确指向性得到提升,末端姿态测量和调节的平滑性和收敛性较好,在机器人控制中具有很好的应用价值。