三维离散元软件的加速可视化方法

付 宏, 黄嘉桐, 马宇涵, 于亚军, 于建群

(1. 吉林大学 计算机科学与技术学院, 长春 130012； 2. 吉林大学 数学学院, 长春 130012；3. 吉林大学 生物与农业工程学院, 长春 130022)

在农业生产领域, 从耕地到农产品种植, 再到农作物的收获、 干燥、 输送、 分级、 加工和包装等过程, 始终存在着散粒物料与农机部件之间接触作用和散粒物料的流动现象. 为分析农机部件在工作过程中的情况, 并进行农机部件的优化设计, 吉林大学数值模拟与计算机仿真课题组开发了一款针对农业工程领域的三维离散元仿真分析软件AgriDEM(agricultural discrete element method). 该软件的特点是: 在农机部件的设计阶段, 可通过农机部件的CAD模型(CAD软件设计图), 进行散粒物料运动过程及农机部件工作过程的仿真模拟, 进而分析所设计农机部件的可行性和合理性； 通过改变农机部件的CAD模型, 分析评价处于不同原理、 不同结构及不同尺寸参数条件下农机部件的工作性能, 以实现农机部件结构方案和尺寸参数的优化.

大部分离散元软件在仿真分析过程中, 当需要计算的散粒物料数量较多时, 由于数据量巨大, 会出现仿真数据可视化时闪烁、 卡顿等问题. 为解决该问题, 方晓健等[1]通过使用GPU加速粒子模拟过程, 同时采用数据到图像的快速转换工作. 上述方法虽从粒子绘制角度出发进行加速处理, 在一定程度上优化了该问题, 但随着整个模拟过程更庞大的数据流入, 仍会超过单机可视化流水线的负荷能力, 此时数据流入阻塞, 会导致显示时卡顿. 邵思睿等[2]通过设置关注视口, 采用固定视角显示方法减少可视化输入的数据量, 初步实现了大规模粒子模拟结果的可视化, 虽有效解决了庞大数据流入问题, 但不能在显示中快速转换视角观察模拟过程.

针对上述问题, 本文对AgriDEM软件可视化模块中的输入数据进行特征提取, 保留在各角度下人眼视野可见的颗粒信息, 同时剔除内部不可见的颗粒信息, 通过降低同一时刻在可视化过程中输入的数据量加快绘制速度, 并在读取剔除后数据的基础上, 使用OpenGL完成离线动画生成及创建出高质量视频图像的输出. 该方法可在仿真演示时任意转换观察视角并改变机械模型大小, 在减轻可视化流水线上负荷的同时, 能进行全局显示和局部显示, 整体提高了显示结果的生成速度, 并解决了可视化流水线中庞大数据量导致的卡顿问题.

1 算法概述

当AgriDEM软件分析计算颗粒材料与农机部件的接触作用时, 在每个或每几个计算时步, 都需将计算结果保存至结果文件中, 保存的计算结果包括： 入料口的形状和位置, 农机部件的形状和位置, 单个颗粒的形状、 位置、 速度和受力等信息. 如果计算的颗粒数量较多, 则保存的结果文件将会很大. 当读取这些保存的结果数据进行可视化时, 由于定时切换显示画面过程, 并占用大量的计算和存储空间[3], 可能超出I/O接口的极限, 将导致显示时闪烁、 卡顿等问题.

对整个模拟过程分析可知, 当计算的颗粒数量较多时, 并不需要读取所有的颗粒数据进行可视化. 用户通常只关心表面或局部颗粒的情况, 如从外观可见颗粒的运动情况[4]等, 这时不可见或被遮挡的颗粒可以不显示. 由于可视化的数据减少, 因此可避免显示时卡顿的发生. 如图1所示, 在显示时因物体之间的遮挡关系及人眼视觉深度等因素影响, 图1(B)中处于中间区域的立方体Centre, 在图1(A)中因各角度都有其他立方体遮挡导致不可见, 但Centre是否绘制对可视化效果无影响. 因此判断一个颗粒是否需要绘制, 可通过对颗粒周围的空间分布情况进行分析. 本文从计算结果文件出发, 通过分析颗粒周围空间内其他颗粒的分布情况, 判断颗粒可见性, 保留并显示粒子群外壳, 建立一种内部单元剔除算法, 从而解决AgriDEM软件显示时的卡顿问题.

图1 颗粒三维空间排布的示意图Fig.1 Sketch map of three-dimensional spatial arrangement of particles

2 算法实现

内部单元剔除算法主要步骤如下： 按颗粒编号依次设为待判断颗粒； 根据待判断颗粒坐标、 半径、 颗粒类型求得颗粒周围空间的大小； 计算待判断颗粒周围空间内其他颗粒的分布情况； 根据分布情况判断该颗粒是否剔除.

本文涉及的参数定义如下： 设依次进行判断是否可见的颗粒为待判断颗粒； 待判断颗粒在建立其周围空间时, 以自身所在全局坐标的位置建立局部坐标系； 局部坐标系的中心设在待判断颗粒球心处, 局部坐标轴的方向向量与全局坐标轴的方向向量平行； 从结果文件中读出的颗粒半径为R, 三维空间内球心坐标为(X,Y,Z), 颗粒类型为Model, 非球颗粒的轴长为Axial length； 待判断颗粒周围空间用Sn表示, 限制空间大小的边界线用Ln表示； 每个待判断颗粒周围最近一层的颗粒总数称为配位数, 用Number表示； 每个子空间Sn内其他颗粒的分布个数称为子空间配位数, 用Number_Sn表示.

2.1 建立颗粒周围空间

通过对局部坐标系中x,y,z的取值划分颗粒周围空间大小, 先考虑xoy平面上x,y的取值范围, 再考虑z方向上z的取值范围.

2.1.1 颗粒周围空间的划分 建立颗粒周围空间时, 在xoy平面, 待判断颗粒投影的圆心落在坐标系原点上. 算法中要计算待判断颗粒周围空间内其他颗粒的分布情况, 因此要保证待判断颗粒为内部颗粒时, 所划分的每个子空间内至少含有一个颗粒的球心坐标. 假设待判断颗粒为半径最大颗粒, 根据二维平面内圆形的特点, 中心圆被包围时, 周围有6个相切圆, 因此尝试将中心圆周围区域划为6个子区域.

如图2(A)所示,S1～S6分别表示6个子区域,L1～L8为限制区域大小的边界线. 因为颗粒周围区域均匀划分, 故周围6个圆形的位置和选取的边界线位置对区域的划分无影响, 为方便分析, 本文按图2所示选取边界线(深色颗粒为待判断颗粒). 图2中α为区域数为6时单个区域的范围,β为区域数改变时新划分的区域范围,γ为α和β区域的差值. 假设选取的子区域个数小于6, 则单个区域变大, 在图2(C)和(D)所示情形下, 区域β中均有一个圆心落入, 但实际上区域β中的γ部分对待判断颗粒的遮挡情况不同, 若确定γ处分布, 还需参照邻近区域再次判断； 假设选取子区域个数大于6, 则单个区域变小, 如图2(B)所示情形, 区域β中颗粒分布情况仍需参照邻近区域判断. 因此, 将xoy平面划分为6个子区域最合理.

图2 区域的划分Fig.2 Division of region

为方便计算, 令z方向上选取最小层数2, 划为上下两层, 颗粒周围空间整体划分如图3所示, 其中深色颗粒为待判断颗粒. 图3(A)中子区域S3与图3(B)中子空间S3对应, 空间分为上下两层. 根据图3的空间划分, 可以求出范围：

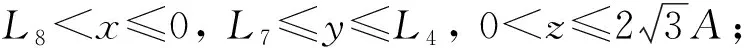
其中A,B为确定空间大小的参数.

图3 颗粒周围空间的整体划分Fig.3 Overall division of particles around space

2.1.2 确定颗粒周围空间大小 颗粒周围空间范围分3种情形考虑： 尺寸均一球颗粒、 尺寸不同球颗粒和非球颗粒[5].

图4 颗粒堆积紧密情形Fig.4 Tight packing of particles

图5 颗粒堆积有序情形Fig.5 Ordered packing of particles

颗粒堆积松散情形如图6所示, 其中深色颗粒为待判断颗粒. 图6(A)中子空间S3包含的浅色颗粒与图6(B)中子区域S3包含的浅色圆形对应. 在xoy平面上, 为中心圆设置编号2, 对区域S2,S3,S4内圆形依次编号. 若使包围待判断颗粒的其他颗粒球心坐标均落在所划分的子空间内, 编号为5的圆心应在区域S2范围内, 此时应求出圆2～5的极值距离, 参照图6(B), 可求出xoy平面上圆2～4的距离为

由于颗粒是随机堆积的, 在x,y,z方向上均可能出现这种极值情况, 因此考虑该情况下, 颗粒周围最小空间应满足控制参数A,B取值为R.

颗粒分散[7]的情形如图7所示, 其中深色颗粒为待判断颗粒. 同一子空间上下层不会均包含其他颗粒的球心坐标, 在这种情况下, 空间控制参数A,B取值大于0即可.

图6 颗粒堆积松散情形Fig.6 Loose packing of particles

图7 颗粒分散情形Fig.7 Dispersion of particle

因颗粒在运动过程中的状态随机, 所以颗粒周围空间的范围要满足颗粒的各种运动状态. 根据上述4种状态控制参数A,B的取值, 可得出当颗粒尺寸均一时, 颗粒周围空间大小参数为A=B=R.

2) 尺寸不同球颗粒. 尺寸不同球颗粒在运动过程中, 会出现堆积和分散两种状态, 如图8所示. 图8(C)为颗粒分散时, 同一子空间上下层不会同时包含其他颗粒的球心坐标, 此时, 空间控制参数A,B取值大于0即可. 图8(A)和(B)中, 无论大颗粒还是小颗粒, 其周围空间范围应足够包含大颗粒. 设待判断的颗粒半径为R待判断颗粒, 则Rmin≤R待判断颗粒≤Rmax. 此时假设待判断颗粒周围都是半径最大颗粒, 参照颗粒尺寸均一时的极值情况, 如图8(D)所示, 可得出当颗粒尺寸不同时, 颗粒周围空间控制参数A,B为

图8 颗粒的不同状态Fig.8 Different states of particles

图9 非球颗粒模型Fig.9 Model of non-spherical particle

3) 非球颗粒. 非球颗粒多为农作物, 如大豆籽粒、 玉米籽粒等[8], 在模拟时以球颗粒为组成球表示, 如图9所示. 由图9可见, 大豆颗粒由4个球颗粒组成, 玉米颗粒由8个球颗粒组成[9], 图9(C)和(F)中深色圆是以非球长轴为直径的圆形. 因此分析非球颗粒时, 只需将非球的各组成球视为一个整体判断. 非球颗粒在运动过程中, 会出现堆积和分散两种状态, 参照尺寸均一球颗粒的情形, 已知非球颗粒的轴长用参数Axial length表示, 可得出颗粒周围空间控制参数为

A=B=(Axial length)/2.

2.2 内部颗粒剔除规则

确定颗粒周围空间大小后, 再计算各子空间内其他颗粒的分布情况, 并根据分布情况判断该颗粒是否剔除. 若每个子空间内分布的颗粒数量均足够将待判断颗粒遮挡住, 则视为待判断颗粒在各视角下均不可见, 剔除该颗粒信息[10].

内部颗粒剔除步骤如下:

1) 根据读出的颗粒半径R或轴长Axial length, 计算出待判断颗粒周围各子空间在局部坐标系的范围；

2) 读出剩余颗粒全局坐标(X,Y,Z)并求出相对局部坐标值；

3) 从全部剩余颗粒中找出局部坐标值满足子空间x,y,z取值范围的颗粒信息；

4) 设子空间配位数初始值Number_Sn=0, 子空间内每找到一个颗粒球心落入, Number_Sn值即增加参数C(C为子空间内该颗粒遮挡比例值), 直到剩余颗粒判断结束；

5) 根据颗粒的3种类型, 依次对尺寸均一球颗粒、 尺寸不同球颗粒、 非球颗粒的剔除规则进行分析.

① 尺寸均一球颗粒. 尺寸大小相同的颗粒, 其周围子空间内至少有一个颗粒能在该方向上将待判断颗粒完全遮挡住, 故每判断出一个球颗粒, 子空间内该颗粒遮挡比例参数C即取值为1.

图10 某子空间内无颗粒球心分布Fig.10 Particle-free core distribution in subspace

当全部剩余颗粒均判断完时, 若Number_Sn值有一个或多个为0, 则说明存在子空间内无颗粒球心落入, 颗粒在该角度下是可见的, 颗粒信息保留. 如图10所示, 深色颗粒为待判断颗粒, 浅色颗粒所在子空间上层无颗粒球心落入.若所有Number_Sn值均大于0, 则说明每个子空间内都有颗粒落入, 此时求各子空间配位数和, 与配位数Number比较, 若不小于则说明该待判断颗粒被其他颗粒完全包围, 可剔除； 否则, 颗粒在某角度下是透过缝隙可见的[11], 颗粒信息保留. 配位数Number取值与颗粒类型、 接触力参数设置有关, 与颗粒大小无关. 本文将尺寸均一球颗粒配位数值定义为14, 如图10周围颗粒数所示.

② 尺寸不同球颗粒. 尺寸大小不同的颗粒, 若待判断颗粒被完全遮挡, 则其周围子空间内需要颗粒数量与空间内颗粒大小有关. 若其子空间内的颗粒与待判断颗粒大小相同, 则一个即可； 若比待判断颗粒小或比待判断颗粒大, 则都需要根据体积比求出所能遮挡住的比值. 因此每判断出一个球颗粒, 子空间内该颗粒遮挡比例参数为

当全部剩余颗粒均判断完时, 若Number_Sn值有多个为0, 则说明存在子空间内无颗粒球心落入, 颗粒在该角度下是可见的, 颗粒信息保留. 若所有Number_Sn值均大于0, 则说明每个子空间内都有颗粒落入, 此时求各子空间配位数和, 与配位数Number比较, 若不小于则可剔除； 否则保留颗粒信息.

当Number=14时, 与颗粒尺寸均一时周围颗粒数目相同. 因为待判断颗粒周围是大颗粒或小颗粒, 其均按体积比计算, 若各子空间配位数和达到14, 则说明其周围颗粒的遮挡体积达到与14个待判断颗粒半径相等的球颗粒遮挡体积, 则可判断为内部颗粒并剔除.

③ 非球颗粒. 判断非球颗粒时, 每个组成颗粒属于哪个非球颗粒都有特定标识, 根据读出的非球类型, 可知其组成球个数, 记为n. 因此每判断出一个组成球颗粒, 子空间内该颗粒遮挡比例参数为C=1/n.

当全部剩余颗粒均判断完时, 若Number_Sn值有多个为0, 则说明存在子空间内无颗粒球心落入, 该非球颗粒在该角度下是可见的, 该非球信息保留. 若所有Number_Sn值均大于0, 则将各子空间配位数值与1比较, 若有子空间值小于1, 则颗粒保留； 若子空间值均大于1, 则求出各子空间配位数和, 并与配位数Number比较(Number=14), 若不小于则可剔除； 否则颗粒信息保留.

单独将子空间内Number_Sn值与1比较, 是因为子空间内有组成球颗粒不代表可以将非球颗粒完全遮挡住, 又因非球颗粒所在周围空间是按半轴长取值划分的, 空间增大会存在某个子空间内非球数量不止一个, 整体判断不出某一空间颗粒数量少的情况. 因此定义每个子空间内球颗粒数目不能少于非球组成数目n.

2.3 算法在可视化中的应用

AgriDEM平台的可视化模块[12]中, 首先使用内存映射方法访问结果文件数据, 调用OpenGL函数绘制图形, 并由定时器控制播放速度. 每当定时器被触发, 就会从结果文件中再次读取边界参数、 入料口参数、 颗粒的几何参数及位置等信息, 绘制仿真演示图像. 同时, AgriDEM平台也可以在显示时选择是否生成高质量视频图像, 用于产品设计的大规模推广[13].

该方法为可选择执行, 当数据规模不大时直接显示, 当数据量较大时再对数据进行精化, 对于同一份结果文件, 只需在首次使用时计算. 图11为算法使用流程.

图11 算法流程Fig.11 Flow chart of algorithm

3 测试结果与分析

为了检验AgriDEM平台可视化系统采用内部单元剔除算法后的显示效果, 对改进后的可视化系统进行测试.

3.1 测试条件

采用Visio Studio 2010开发平台, VC++编程语言, OpenGL编程接口库等开发实现. 硬件配置: 处理器为Intel(R), Core(TM) i7-4790, CPU@3.60 GHz, 显卡为NVIDIA GT 740, 内存为8 GB, 硬盘为931.51 GB, 操作系统为Windows 7(64位). 本文取颗粒密度1.209×103kg/m3, 球颗粒直径6.22～7.34 mm, 服从正态分布， 重力加速度9.8 m/s2, 计算时步1.0×10-4s, 颗粒数目200 000个, 圆筒直径400 mm, 圆筒高度500 mm. 其他参数设置列于表1.

表1部分参数设置

Table 1 Partial parameter setting

3.2 显示效果

使用内部单元剔除方法, 在球颗粒尺寸均一、 尺寸不同、 非球情况下的整体显示效果及x>0时内部显示效果如图12所示. 由图12可观察到内部颗粒已经剔除, 且从外观看不影响整体显示效果. 图13为3种不同颗粒在排种器中的显示效果. 结果表明, 在该方法下, 无论颗粒是堆积还是分散都能较好地完成可视化任务.

图12 不同颗粒的内部与整体显示效果Fig.12 Internal and overall display effects of different particles

图13 不同颗粒在排种器中的显示效果Fig.13 Display effects of different particles in seed-metering device

3.3 结果分析

图14 用本文方法前颗粒下落过程Fig.14 Particle drop process before using our method

图15 用本文方法后颗粒下落过程Fig.15 Particle drop process using our method

结果分析采用20万颗粒物料及圆筒机械部件作为测试数据, 参数见表1. 使用该方法前后进行对比, 每隔10 s颗粒的运动情况如图14和图15所示. 由图14和图15可见, 在保证模拟显示效果的同时, 使用本文方法后显示速度明显加快. 图16为模拟过程帧数对比结果. 由图16可见, 在相同单位时间内, 使用本文方法后的帧率明显提升, 相同单位时间内绘制的时步数更多. 表2为使用本文方法前后的实验对比结果.

表2 使用本文方法前后的实验对比结果Table 2 Comparison of experimental results before and after using our method

图16 模拟过程帧数对比结果Fig.16 Comparison results of number of frames in simulation process

由表2可见, 使用本文算法减轻了可视化流水线上输入的数据量, 模拟用时节省51.54%. 因此, 使用本文算法可加快仿真软件可视化的速度, 显著提高程序的运行效率, 并解决了显示卡顿问题.

综上所述, 本文在AgriDEM平台基础上, 使用内部单元剔除技术对数据进行外观提取, 通过判断颗粒自身周围空间内其他颗粒的分布情况精简数据, 解决了大规模计算时可视化流水线上数据的拥塞问题及显示时的卡顿问题, 使得AgriDEM平台对农机部件和散列物料的建模过程更方便、 直观, 模型参数更准确, 保证了计算结果显示的流畅性和合理性, 提高了工作效率, 改善了用户体验.