基于sigmoid函数的高超声速飞行器自适应姿态控制

,,,

(北京航天自动控制研究所,北京 100854)

0 引言

高超声速飞行器一般是指飞行马赫数大于5的飞行器，由于具备速度快、射程远的特点，可以实现体系作战中远程精确打击的目的[1]。相比于传统弹道导弹机动能力弱、易于拦截等特点，由于高超声速滑翔飞行器兼具飞行跨度大、隐蔽性好、作战效能高等显著优势，使得它存在着巨大的潜在军用与民用价值，近些年来越来越受到各个军事强国的重视。

高超声速飞行器姿态控制系统的主要任务是跟踪制导律生成的制导角指令信号，起着跟踪制导指令以及稳定飞行器姿态的作用，对高超声速飞行器安全再入和完成飞行任务具有重要意义。飞行速度快，飞行包络大，强耦合、快时变，强不确定性等特点，给控制器的设计带来了较大的困难与挑战，因此飞行器控制器设计也是制约高超声速飞行器发展的重要因素之一[2-4]。

由于再入过程复杂环境和剧烈变化，通常无法获得精确的模型参数，相关参数存在摄动和不确定性，会引起力矩分配的误差，使得实际力矩与期望力矩存在偏差，此外，外界的扰动如风干扰等会影响飞行器姿态的响应，因此单纯使用线性控制很难达到期望的控制性能。Smith 等[5]将鲁棒线性参数调整控制应用到 X-33 的姿态控制中，但设计的增益数目较大、对模型精度要求较高。Hu等[6]基于扩张状态观测器设计了高超声速飞行器模糊自适应控制器，具有良好的抑制干扰效果。自适应控制是依据对象的输入输出数据，不断的辨识模型参数和修正对模型的估计，因而具有不依赖精确数学模型、仅需较少验前知识等显著优点。ESO作为自抗扰控制器(active disturbance rejection control, ADRC)的核心，能够在仅需系统输出和控制量输入的条件下，实现对未建模动态和外扰总作用量的准确估计，并实现对其补偿，因而具有较强的鲁棒性和一定的抵抗干扰能力，在许多复杂的非线性控制问题中获得成功应用[7-8]。

本文采用非线性动态逆的思想设计主体控制器，基于“时标分离”原理，将飞行器分为快、慢两个回路设计姿态控制器，以保证闭环系统的全局稳定，利用神经网络中Sigmoid函数兼具线性与非线性的特征，分别从俯仰、偏航和滚动3个通道构造跟踪控制律。考虑到再入过程环境扰动以及不确定性的影响，利用ESO对扰动进行估计和补偿，可以有效提升控制系统的鲁棒性和自适应性。

1 飞行器再入数学模型

为了研究高超声速飞行器再入飞行过程中姿态控制问题，需要先对其再入飞行过程进行数学建模。由于实际飞行中存在众多实际工程问题，目前很难完成真实飞行器模型的建立。在确保仿真结果与实际飞行偏差合理的条件下，简化了飞行器建模的相关信息，在建模过程中有如下假设：

1)建模过程中假设地球为圆球；

2)假定飞行器为刚体，忽略飞行过程中机体的弹性变形；

3)假设机体为面对称结构，即认为惯性积Ixz=Iyz=0；

4)假设飞行器再入过程中无动力；

5)再入过程采用BTT控制设计，在整个过程中保持侧滑角为零度，侧力为零。

在航迹坐标系下建立飞行器质心动力学方程，在机体坐标系下建立飞行器再入绕质心旋转运动学和动力学方程，描述飞行器运动状态的变量包括速度V、弹道倾角θ、弹道偏角ψs、攻角α、侧滑角β、倾侧角γS以及角速度ωx、ωy和ωz,运动方程如式(1)所示

(1)

式中，D、L、S分别表示飞行器再入过程中的阻力、升力和侧力；m为飞行器质量；Ix、Iy、Iz分别飞行器三轴的主转动惯量；Ixy为惯量积；Mx、My、Mz分别为滚动力矩、偏航力θ矩和俯仰力矩，具体计算过程参考文献[9]。

2 飞行器控制器设计

再入飞行器快变、慢变的差异性显著。由于角度的变化是角速度在一段时间内的积分值，故角速度的变化可以理解为瞬间的，而角度的变化则是时间累积而来的，故基于“时标分离”原理，只要快回路的响应速度为慢回路响应速度的5至10倍，可以将高超声速飞行器分为快、慢两个回路，内回路为3个角速度的控制回路，外回路为气流角控制回路，结构如图1所示。

图1 快慢回路结构图

2.1 神经网络Sigmoid函数

Sigmoid函数是神经网络中一类激励函数，又称“S型函数”，常被用作神经网络的阈值函数，具有单调性、光滑性、饱和性等明显特征[10]，其表达式为：

(2)

从式(2)中可以看出，该函数严格单调递增，且上下界在0～1范围内，对式(2)引入幅值系数a和指数因子b，并作简单线性变换，使其阈值为(-0.5a,0.5a)的奇函数，表示为：

(3)

其中:值系数a用于调节Sigmoid函数的幅值，通过改变指数因子b的值可以调节近似线性工作区间的范围。对式(3)在x=0处进行泰勒展开：

(4)

从式(4)中可以看出，在x=0的邻域内，Sigmoid函数可以近似为线性函数，且曲线斜率较大，而当x远离零点，非线性特性占主导部分，但此时曲线相对平滑，斜率较小，图2给出了在幅值增益a=2时，在不同指数因子b下对应的Sigmoid函数曲线。

图2 不同指数因子b对应Sigmoid函数曲线

从图2中可以看出，函数S(x)兼具线性形式和非线性特性形式，符合工程界实践总结出来的规律——“大偏差小增益，小偏差大增益”，用Sigmoid函数构造控制律时，具有快速、消除颤阵、避免控制量饱和等显著优点。

2.2 非线性动态逆控制器设计

利用旋转运动学方程来描述姿态角的变化，该组微分方程状态变量为α,β,γS，输入为ωx,ωy,ωz。由于转动角速度不能直接作为控制量，还需描述转动角速度的变化。即系统的状态变量为α,β,γS和ωx,ωy,ωz，控制输入变量为Mx,My,Mz[11]。这3个力矩可以通过控制飞行器的气动舵面偏转实现，具体设计思路如图3所示。

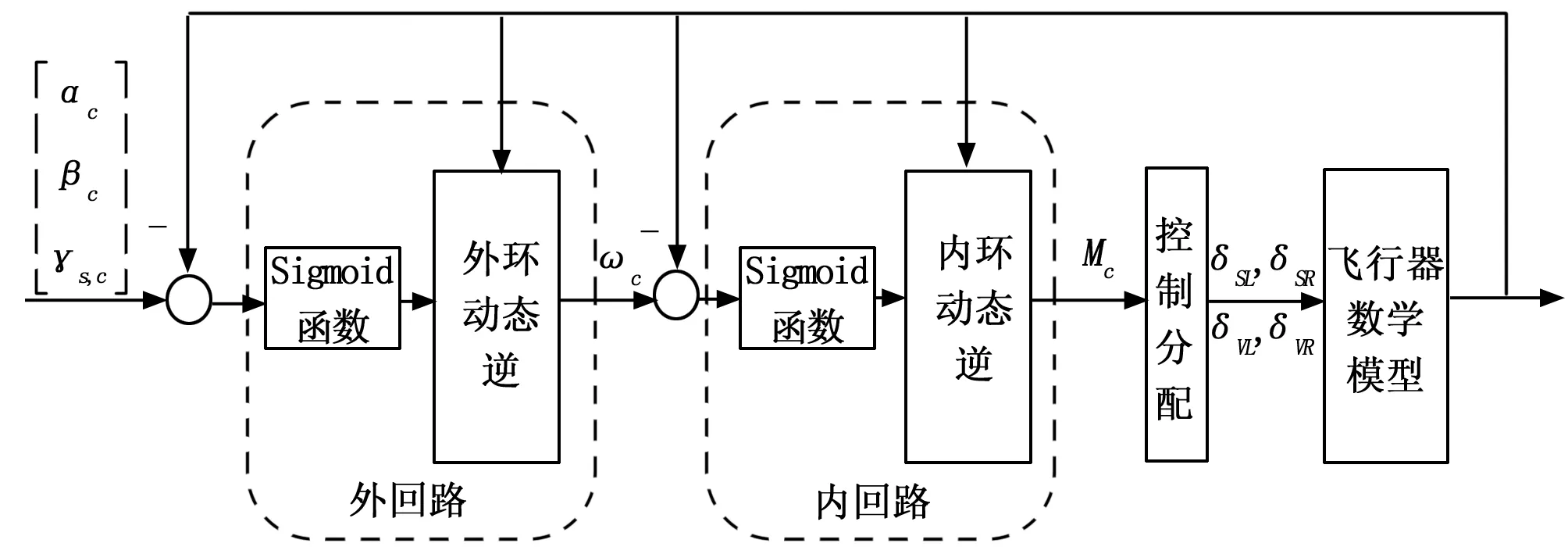
图3 动态逆控制系统结构图

2.2.1 非线性动态逆内环控制器设计

(5)

(6)

2.2.2 非线性动态逆外环控制器设计

将(1)式中飞行器绕质心旋转运动学方程简化成：

(7)

其中:

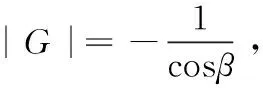
ωc=G-1[υ-f]=

(8)

(9)

2.3 基于ESO的自适应控制器设计

再入过程中参数的摄动和不确定性会引起力矩分配的误差，使得实际力矩与期望力矩存在偏差，此外，外界的扰动也会影响飞行器姿态的响应。利用ESO不依赖精确模型即可将模型中未建模部分，内部摄动以及扰动观测出来的特点[12]，设计基于ESO的自适应补偿系统，叠加到2.2中设计的非线性动态逆控制器中，以弥补单纯使用动态逆对不确定性鲁棒性差的问题，基于ESO的自适应控制结构图如图4。

图4 基于ESO的自适应控制结构图

2.3.1 基于ESO的内环自适应控制器设计

将式(1)中飞行器绕质心旋转动力学方程表示为：

(10)

飞行器姿态控制输入与气动参数矩阵gδ,M有关，取理论气动参数下gδ,M的标称值为g0，同理将f分解为标称值f0和不确定项Δf，式(10)可等效为：

(11)

令U0=g0Mδ，a(t)=Δf+ΔU，即可配置三通道二阶扩张状态观测器：

e=z1-ωi(i=1,2,3)

(12)

对于式(12)，选择合适的连续函数g1和g2使得，eg(e)>0，则上式能准确跟踪系统(11)。本文采用线性关系，取g1(e)=2ηe，g2(e)=η2e，则系统(11)的特征方程为(s+ω)2，对期望信号有较好的跟踪效果，即z2收敛到a(t)，a(t)即为飞行器内环的总的误差，由a(t)可以推出内环需要补偿的控制力矩Mδ,compensation：

(13)

由此得到控制器输出的总的控制力矩：

Mδ,C=Mδ-Mδ,compensation

(14)

2.3.2 基于ESO的外环自适应控制器设计

将式(1)中飞行器绕质心旋转运动学方程表示为

(15)

f项中存在参数不确定；此外，飞行器实际运动中，存在未知外部干扰，未建模动态等，建模取为Δ，将以上不确定性视为不确定项a(t)，因此可将式(15)等效为：

x=f+a(t)+U

(16)

其中:a(t)=Δ，Δ为系统外部干扰，未建模动态等；U=gω，即可配置三通道二阶扩张状态观测器：

e=z1-x

(17)

式(17)中，e、z1、z2均为三维向量，同理取β1=2η，β2=η2，使系统(17)的特征方程为(s+ω)2，对期望信号能有较好地跟踪效果，即z2收敛到a(t)，a(t)即为飞行器外环的总的误差，由a(t)可以推出需要内环需要补偿的控制角速度ωcompensation，由3.2.2知矩阵g总是可逆的，故：

ωcompensation=g-1a(t)

(18)

由此得到控制器输出的总的期望角速度：

ωC=ω-ωcompensation

(19)

3 仿真验证

3.1 跟踪阶跃指令

若飞行器再入过程中得到30°倾侧角和8°攻角的制导角指令，当式(6)和式(9)中控制律分别采用PID控制和Sigmoid函数控制时，图5为控制器仿真结果。

图5 攻角倾侧角同时阶跃气流角跟踪曲线

由仿真结果可以看出，攻角、侧滑角和倾侧角都能够无静差的跟踪指令信号，验证了设计的非线性动态逆控制器具有较好的控制品质。当采用Sigmoid函数构造控制律时，相比于PID控制时，侧滑角跟踪速度明显变快、超调减小，攻角和倾侧角也有一定的提升，验证了Sigmoid函数具有良好的控制品质。

3.2 参数拉偏仿真

飞行器质量偏差范围±1%，气动偏差范围±10%，大气密度偏差范围±10%，取所有拉偏值的最大正值，在飞行器得到10°倾侧角和5°攻角的阶跃指令下，拉偏与不拉偏飞行仿真结果如图6所示，攻角和倾侧角跟踪情况放大情况如图7所示。

图6 拉偏情况下动态逆控制气流角跟踪曲线

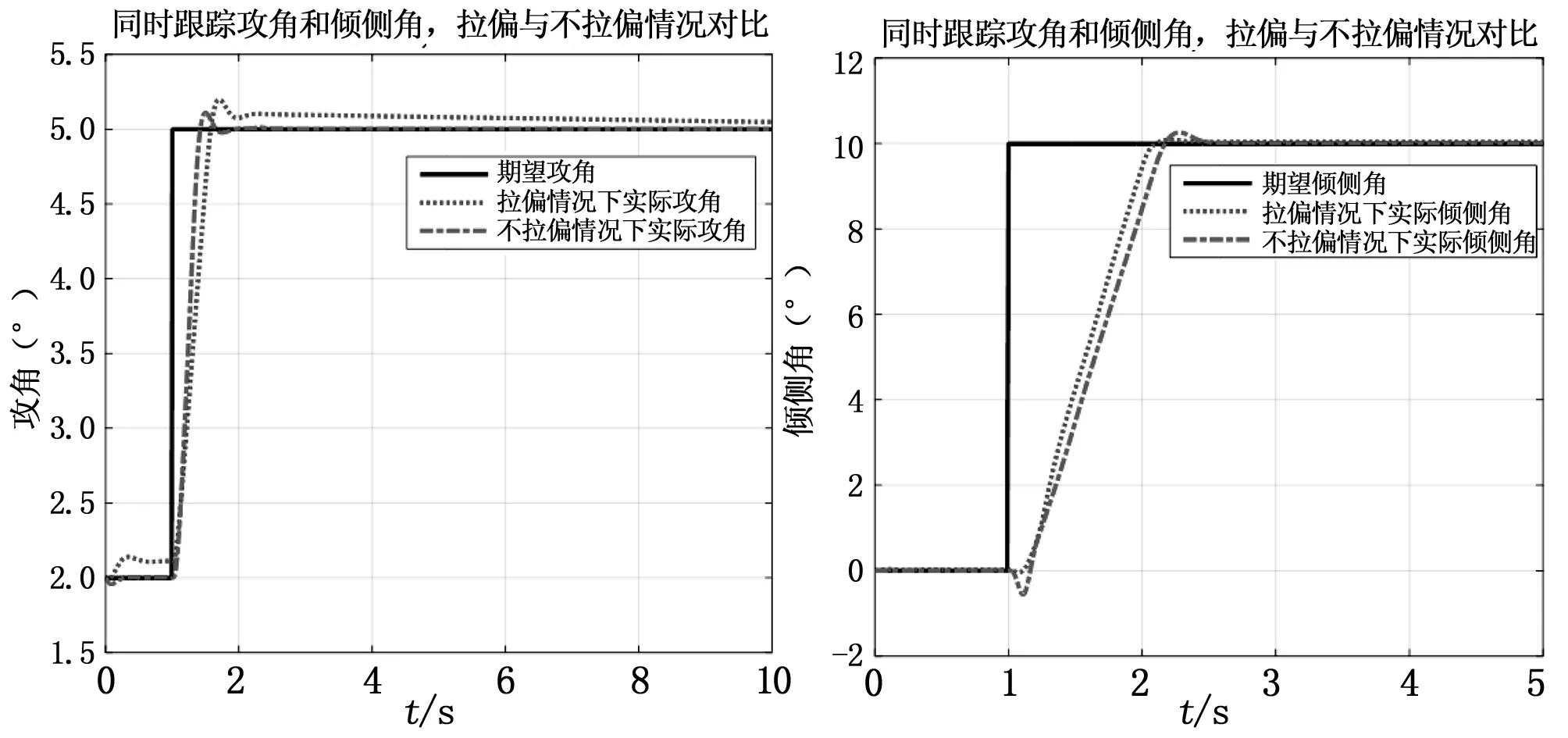
图7 拉偏条件下仅动态逆控制攻角/倾侧角跟踪曲线放大图

从图7可以看出，拉偏情况下单纯使用动态逆控制，攻角跟踪速度变慢、超调增大且稳态误差明显变大，侧滑角和倾侧角抖动明显。

在加入ESO补偿和单纯使用动态逆控制的攻角飞行结果对比如图8所示。

图8 加ESO补偿和仅动态逆控制的攻角响应对比

拉偏条件下加ESO补偿的控制器攻角跟踪速度明显变快、超调减小且稳态误差明显减小，侧滑角和倾侧角响应也有一定的提升，可知基于ESO的自适应控制器对控制系统性能提升明显。

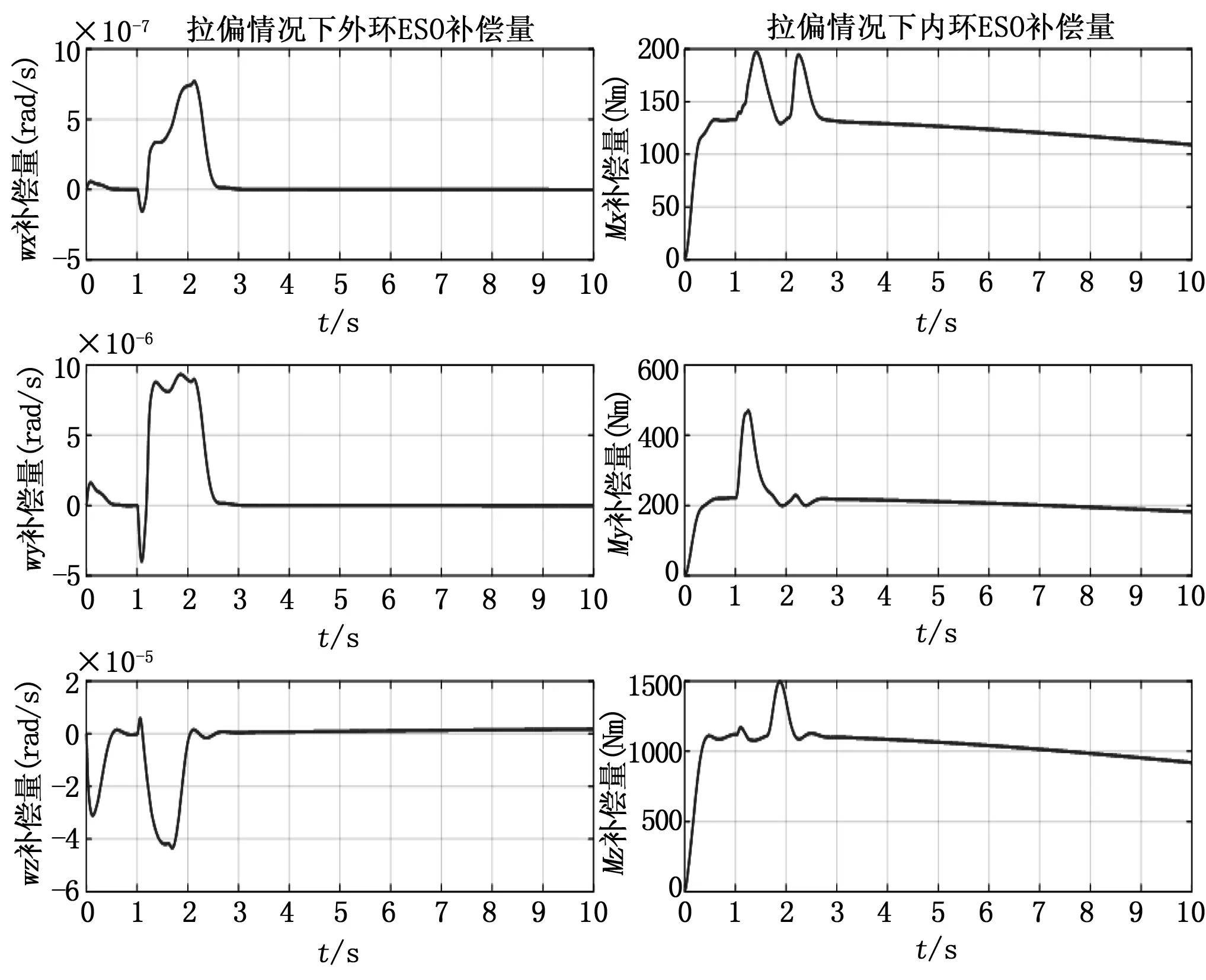
图9 ESO观测的内外环补偿量

在姿态控制过程中，加入气动数据拉偏、大气密度拉偏和飞行器参数拉偏主要影响飞行器实际矩，使得飞行器的内环的实际模型与控制器所用模型存在偏差，但这些拉偏对外环模型影响并不大，图9中基于ESO观测的内外环各通道补偿量也验证了这一点。

3.3 风干扰仿真

将360°均分为8个方向，每个方向分别加入水平风干扰后，对10°倾侧角和5°攻角的阶跃指令信号进行跟踪，仿真结果如图10所示。

图10 风干扰条件下气流角跟踪对比

仿真结果可以看出，加入基于ESO补偿的控制系统具有较好的抵抗风干扰能力。

4 结论

本文研究了基于sigmoid函数的高超声速飞行器自适应姿态控制方法，首先在给定假设条件下建立了高超声速飞行器再入数学模型，以改进型Sigmoid函数分通道设计控制律，分内外环设计了高超声速飞行器动态逆控制器，并在跟踪阶跃指令和参数拉偏条件下进行仿真分析，针对单纯使用动态逆控制鲁棒性弱的特点，开展基于ESO的自适应控制技术研究，验证加入ESO补偿的控制系统具有较强抗干扰能力。